What are the 3 names of triangles?
Answers
The 3 names of triangles:
Scalene, Isosceles. Equilateral.
What are triangles?
Three vertices make up a triangle, a three-sided polygon. The triangle's angles are formed by a point where the three sides are joined end to end. The triangle's three angles add up to a total of 180 degrees.
Triangles fall into one of three categories depending on how long their sides are: Scalene. Isosceles. Equilateral.
Scalene : All sides have different lengths
Isosceles : 2 sides are of equal length
Equilateral : All sides are of equal length
To learn more about the triangle from the given link
https://brainly.com/question/1058720
#SPJ4
Related Questions
Ms. Keenan is a high school teacher who wants to know how much time students spend studying each day. She finds that the average student spends 3.00 hours a day studying (s - 0.75). Assuming that studying hours is normally distributed, what percentage of students study less than 2.50 hours a day?
© 25.14 percent
© 19.15 percent
© 10.93 percent
© 24.86 percent
Answers
The requried, percentage of students who study less than 2.50 hours a day is approximately 25.14 percent.
What is the Z -a score?A Z-score is stated as the fractional model of data point to the mean using standard deviations.
We need to convert 2.50 hours to a standard score (z-score) using the formula,
z = (x - μ) / σ
where x is the value we want to convert, μ is the mean, and σ is the standard deviation.
z = (2.50 - 3.00) / 0.75
z = -0.67
This means that 2.50 hours is 0.67 standard deviations below the mean.
We can use a standard normal distribution table or a calculator to find the percentage of the distribution that falls below this standard score. For example, using a standard normal distribution table, we can look up the area to the left of z = -0.67 and get:
P(z < -0.67) = 0.2514
So the correct answer is (a) 25.14 percent.
Learn more about the z-score here:
brainly.com/question/13793746
#SPJ1
7. The Taylor Rule states that the central bank should set the short-term nominal interest rate (i)
based on the inflation gap [the difference between inflation (3.14) and desired inflation (3.14*)] and the
output gap (the percentage difference between real GDP (Y) and potential GDP (Y*) An
example of a Taylor Rule would be the formula
i - 3.14 = 1.5 +0.5(3.14-3.14*) +0.5 (Y-Y*/Y*)
The term on the left-hand side is the real interest rate. Consider the following table
Inflation rate (3.14), %
Target inflation rate (3.14*), %
Output gap, %
Real interest rate
Nominal interest rate
Base Scenario Scenario B Scenario C
4.0
20
2.0
20
0.0
20
20
20
00
a. Fill in the real and nominal interest rates chosen by the policy maker in the base scenano
b. How does scenario B differ from the base scenario in terms of the inflation and output gaps?
Calculate the real interest rate. Has the real interest rate moved in the direction that would
move the inflation rate toward its target?
c. How does scenario C differ from the base scenario in terms of the inflation and output gaps?
Calculate the real interest rate. Has the real interest rate moved in the direction that would
move output toward the potential level?
d. Suppose a new chair of the central bank is appointed and she switches to a new policy rule of
the form given in the next equation. Recalculate the real and nominal interest rates for the
three scenarios. What has been the effect of the change in weights?
i-3.14=1.5 +0.75(3.14-3.14*) +0.25(Y-Y*/Y*)
Answers
The weight on the inflation gap has increased from 0.5 to 0.75. The real interest rate is 16.86% and Nominal interest rate is 20%
a. In the base scenario, the real interest rate will be 20%, and the nominal interest rate will be 20%.
b. In scenario B, inflation rate will be higher (4%) compared to the base scenario (3.14%).
Output gap is 0% in both the scenarios, however, in the base scenario inflation gap is 0% (3.14 - 3.14) and in scenario B, inflation gap is 0.86% (4 - 3.14).
Now, let's calculate the real interest rate.
Real interest rate in base scenario = 20% - 3.14%
= 16.86%.
Real interest rate in scenario B = 20% - 3.14% + 1.5 + 0.5 (4-3.14) + 0.5 (0-0/0)
= 19.22%.
The real interest rate has moved in the direction to move inflation rate towards its target.
c. In scenario C, the output gap will be 20% compared to 0% in the base scenario.
Inflation gap is 0% in both the scenarios
Inflation rate is 3.14% and in scenario C, inflation rate is 2%.
Let's calculate the real interest rate. Real interest rate in the base scenario = 20% - 3.14%
= 16.86%.
Real interest rate in scenario C = 20% - 2% + 1.5 + 0.5 (3.14 - 3.14) + 0.5 (20-0/20)
= 20.15%.
Real interest rate in scenario C = 20% - 2% + 1.5 + 0.75 (3.14-3.14) + 0.25 (20-0/20) = 18.78%.
The new policy rule has changed the weight of the output gap in the Taylor Rule from 0.5 to 0.25.
For more related questions on inflation gap:
https://brainly.com/question/31419643
#SPJ8
Calculus please help

Answers
f(x) is discontinuous.
Since LHS ≠ RHS ≠ f(x).
What is a function?A function is a relationship between inputs where each input is related to exactly one output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
here, we have,
We have,
f(x) = x + 1, for x ≤ 2
f(x) = 2x - 1, for 1 < x < 2
f(x) = x - 1, for x < 1
Now,
A x = 1
LHS of f(x) = lim f((h - 1)) = (h - 1 - 1) = 0 -2 = -2
RHS of f(x) = lim f(h + 1) = (2(h + 1) - 1) = 2h + 2 - 1 = 0 + 1
f(1) = x + 1 = 1 + 1 = 2
We see that,
LHS ≠ RHS ≠ f(x)
So,
f(x) is not continuous, it is discontinuous.
Thus,
f(x) is discontinuous.
Learn more about functions here:
brainly.com/question/28533782
#SPJ1
The complete question.
Show that the following functions are continuous or discontinuous at x = 1.
f(x) = x + 1, for x ≤ 2
f(x) = 2x - 1, for 1 < x < 2
f(x) = x - 1, for x < 1
At the movie theatre, child admission is $6.30 and adult admission is $9.80. On Monday, twice as many adult tickets as child tickets were sold, for a total sales of $673.40. How many child tickets were sold that day?
Answers
Answer:
26 child tickets
Step-by-step explanation:
Let's assume the number of child tickets sold is "x".
According to the given information, the number of adult tickets sold is twice the number of child tickets sold, so the number of adult tickets sold would be "2x".
The total sales from child tickets can be calculated by multiplying the number of child tickets by the child admission price:
Total sales from child tickets = $6.30 * x
Similarly, the total sales from adult tickets can be calculated by multiplying the number of adult tickets by the adult admission price:
Total sales from adult tickets = $9.80 * (2x)
The total sales from both child and adult tickets is given as $673.40:
Total sales from child tickets + Total sales from adult tickets = $673.40
Substituting the expressions for the total sales:
$6.30 * x + $9.80 * (2x) = $673.40
Simplifying the equation:
6.30x + 9.80(2x) = 673.40
6.30x + 19.60x = 673.40
25.90x = 673.40
Dividing both sides by 25.90:
x = 26
Therefore, 26 child tickets were sold on Monday.
Answer:We can solve this problem by using algebra. Let × be the number of child tickets sold and y be the number of adult tickets sold. We know that y = 2x (twice as many adult tickets as child tickets were sold) and that the total amount of money made from ticket sales was $278.20.
So we can write the equation 6.3x + 9.8y =
278.2 and substitute y = 2x into it to get 6.3x +
9.8(2x) = 278.2.
Simplifying this expression gives us 6.3x + 19.6x = 278.2.
Combining like terms gives us 25.9x = 278.2.
Solving for x gives us x = 10.74.
Since we can't sell a fraction of a ticket, we round up to 11 child tickets.
We know that y = 2x, so y = 2(11) = 22.
So 11 child tickets and 22 adult tickets were sold.
As part of a survey, 2400 people were asked to name their favorite sport to watch. The table below summarizes their answers. This information is also presented
as a circle graph.
Find the central angle measure, x, for the Baseball slice in the circle graph. Do not round.
Sport
Football
Soccer
Baseball
Basketball
Hockey
Other
Percentage
of People
29%
9%
14%
8%
8%
Soccer
Baseball
Basketball
Football
Other
Hockey

Answers
The central angle measure, x, for the Baseball slice in the circle graph is 50.4 degrees.
Given that, a survey was conducted in which 2400 people were asked to name their favorite sport to watch and the table below shows their answers: Sport percentage of people are:
Football 29%
Soccer 9%
Baseball 14%
Basketball 8%
Hockey 8%
Other 32%
We need to find the central angle measure, x, for the Baseball slice in the circle graph.
For this, we need to use the formula that gives the central angle measure in degrees for a sector of a circle:
Central angle measure = (Percentage/100) × 360°
Now, using the above formula, we can calculate the central angle measure for each sport as shown below:
Football: (29/100) × 360° = 104.4°
Soccer: (9/100) × 360° = 32.4°
Baseball: (14/100) × 360° = 50.4°
Basketball: (8/100) × 360° = 28.8°
Hockey: (8/100) × 360° = 28.8°
Other: (32/100) × 360° = 115.2°
The sum of all central angle measures should be 360°, which is the measure of a full circle.
So we can check if the calculations are correct: 104.4° + 32.4° + 50.4° + 28.8° + 28.8° + 115.2° = 360°
We see that the sum is indeed 360°, so the calculations are correct. The central angle measure for the Baseball slice is 50.4°.
Therefore, the central angle measure, x, for the Baseball slice in the circle graph is 50.4 degrees.
For more such questions on central angle, click on:
https://brainly.com/question/10945528
#SPJ8
. Trevor mows 5 times as
many lawns in the
summer as he does in
the fall. If he mows 20
lawns in the summer,
how many does he mow
in the fall?

Answers
Answer:
4 lawns
Step-by-step explanation:
20/5
20/5=4
Hope this helps
Solve for n. 8^ 12÷8^3=8^n
Answers
Answer:
9\(\frac{8^{12}}{8^3}=8^n\quad :\quad n=9\)
Step-by-step explanation:
What is the rule for finding the sum of two real numbers with unlike signs?
Answers
Answer:
you have to subtract the absolute values.
Step-by-step explanation:
Salim has a picture book with 124 pages in it. He read 1/4 of the book to his little brother. How many pages did he read?
Answers
Answer:
31
Step-by-step explanation:
124/4 = 31 pages per one fourth of the book
If your brother reads one fourth of the book then he reads 31 pages.
31
Step-by-step explanation:
divide 1/4 by 24 and 31 should be the answer
TASK 2: Awards DinnerTran is in charge of the school's Awards Dinner. She set up the multi-purpose room with a stage in front and round tables for parents, students, and family membersto sit around for dinner. Below is the floor plan that she drew for the event.StageCLUE Illuminate EducationIncSign out11US 01:09hp

Answers
According to the image each table has an amount of 8 seats, and there are
On October 12, 2020, the number of new cases of Covid 19 in Milwaukee was 235. On Oct. 22, 2020, the number of new cases in Milwaukee was 395.
a. Create an exponential model for new cases in terms of days.
b. Based on your model, what would be the number of new cases on Oct. 31, 2020?
c. The actual number of new cases on Oct. 31, 2020, was 1043. How well does this fit your model?
Answers
a. To create an exponential model for new cases in terms of days, we can use the formula: y = a * b ^ x, where y is the number of new cases, x is the number of days since the first observation, and a and b are constants that we need to determine. Using the two data points given, we can set up a system of equations:
235 = a * b ^ 0
395 = a * b ^ 10
Solving for a and b, we get:
a = 235
b = (395/235)^(1/10) = 1.067
Therefore, the exponential model for new cases in Milwaukee is:
y = 235 * 1.067 ^ x
b. To find the number of new cases on Oct. 31, 2020, we need to plug in x = 19 (since Oct. 31 is 19 days after Oct. 12) into the model:
y = 235 * 1.067 ^ 19 = 1018.5
Therefore, based on the exponential model, we would expect around 1019 new cases on Oct. 31, 2020.
c. The actual number of new cases on Oct. 31, 2020, was 1043. This is higher than the predicted value of 1019, but not by a huge margin. Overall, the model seems to fit the data reasonably well, especially considering that there are many factors that can affect the number of new cases in a given area, and that the model is based on only two data points. However, it is worth noting that the exponential model assumes that the growth rate of new cases remains constant over time, which may not be a realistic assumption in the long run.
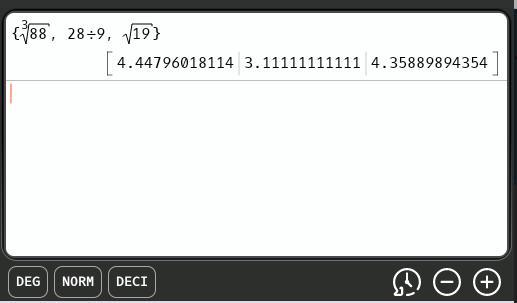
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
Since speed is equal to distance divided by time, what would distance be equal to?
Answers
The in this case, the distance covered by the car would be 120 miles. The equation Distance = Speed * Time allows us to determine the distance covered by an object when the speed and time taken are known.
To determine distance, we can rearrange the formula for speed:
Speed = Distance / Time. By multiplying both sides of the equation by Time, we can isolate Distance.
Distance = Speed * Time
The formula indicates that distance is equal to the product of speed and time. By multiplying the rate at which an object moves (speed) by the duration of travel (time), we can determine the total distance covered during that period.
The equation Distance = Speed * Time represents the relationship between distance, speed, and time.
It states that the distance covered is equal to the product of the speed at which an object is moving and the time it takes to travel that distance.
For example, if a car is traveling at a constant speed of 60 miles per hour for 2 hours, the distance it would cover can be calculated as follows:
Distance = 60 miles/hour * 2 hours = 120 miles.
For more such questions on Distance:
https://brainly.com/question/28551043
#SPJ8
length of a rectangle is 3 times its width. If the length is 9cm what is the area of the rectangle
Answers
Answer:
I think it's 27
because length is 3 times its width
A six meter long ladder leans against a building. If the ladder makes an angle of 60° with the ground. How far up the wall does the ladder reach? (Round to the nearest tenth)
Answers
Step-by-step explanation:
step 1. This is a 30-60-90 triangle where the side opposite the 30° is the smallest and represented as x, the side opposite the 60 ° is the middle length at x(sqrt(3)) and the side opposite the 90° is the longest side at 2x. note: sqrt is the square root.
step 2. The ladder is 6m and is the 2x side.
step 3. The wall is across from the 60° side and is the x side.
step 4. if the 2x side is 6m then the x side is 3m.
step 5. The ladder is 3m up the side of the house.
There are 100 students enrolled in our school. 3/5 of the students are boys. How many students are girls?
Answers
Answer:
2/5 are girls so 40
Step-by-step explanation:
100 divided by 5 is 20.
BOYS: 20 x 3= 60
GIRLS: 20 x 2= 40
60+40=100
Hope this helps (:
9(2n+1) simplify expression I will mark brainliest correct answer
Answers
Answer:
18n+9 i think
Step-by-step explanation:
Which number when placed in the blank makes the inequality false

Answers
ANSWER
OPTION A
STEP-BY-STEP EXPLANATION:
The inequality given is written below
----------- > 8
Let the unknown number be x
Since x is greater than 8, then x must be any number greater than 8
Recall that, the absolute value of a real number is x, denoted |x|, which is the non-negative value of x without regard to its sign.
According to the option
|1| = 1
|-9| = 9
|10| = 10
|-13| = 13
Hence, 9, 10, and 11 are greater than 8
The only number, when placed in the blank that will make the inequality false, is 1 because it is less than 8
Write a fraction that is equivalent to 3/5 that has a denominator of 20.
5
15
20
20
12
12
20
3
20
Answers
Answer:
12/20
Step-by-step explanation:
\(\displaystyle \frac{3}{5}=\frac{3}{5}\cdot\frac{4}{4}=\frac{12}{20}\)
The answer is:
12/20In-depth-explanation:
The denominator of 3/5 is 5. To get from 5 to 20, we multiply it by 4.
We need to multiply both the numerator and the denominator by 4, so we do this:
\(\sf{\dfrac{3\times4}{5\times4}}\)
\(\sf{\dfrac{12}{20}}\)
Hence, the answer is 12/20.Greg paid $324.50 for guitar lessons. He paid a $124.50 registration fee and $40 for each week he was enrolled in lessons. What is w, the number of weeks Greg was enrolled in guitar lessons?
Answers
The circumference of the cylinder below is 6 cm and the height is 8 cm. What is the curved surface area of the cylinder? If your answer is a decimal, give it to 1 d.p. circumference = 6 cm
8 cm
Answers
The curved surface area of the cylinder is 48.06 cm².
The circumference of a cylinder is given by the formula:
C = 2πr
where C is the circumference and r is the radius of the base.
In this case, the given circumference is 6 cm.
So, 6 = 2πr
r = 6 / (2π)
r ≈ 0.955 cm
Now, the curved surface area (CSA) of the cylinder using the formula:
CSA = 2πrh
Given the height as 8 cm, we can substitute the values into the formula:
CSA = 2π(0.955 cm)(8 cm)
CSA ≈ 48.06 cm²
Therefore, the curved surface area of the cylinder is 48.06 cm².
Learn more about Curved Surface Area here:
https://brainly.com/question/30816589
#SPJ1
The sum of the present value of 1 paid at the end of n periods and 1 paid at the end of 2n periods is 1. Find (1 i) 2n
Answers
Answer:
\((1 + i)^{2n} = \frac{4}{(-1 \± \sqrt{5})^2}\)
Step-by-step explanation:
Using Present Value formula, we have that:
The present value at end of n period is
\(PV_1 = \frac{1}{(1 + i)^n}\)
The present value at end of 2n period is
\(PV_2 = \frac{1}{(1 + i)^{2n}}\)
\(Sum = PV_1 + PV_2\)
And
\(Sum = 1\)
So, we have:
\(PV_1 + PV_2 = 1\)
Substitute values for PV1 and PV2
\(\frac{1}{(1 + i)^n} + \frac{1}{(1 + i)^{2n}}= 1\)
Solving for:
\((1 + i)^{2n\)
\(\frac{1}{(1 + i)^n} + \frac{1}{(1 + i)^{2n}}= 1\)
This can be expressed as
\(\frac{1}{(1 + i)^n} + (\frac{1}{(1 + i)^{n}})^2= 1\)
Let
\(a = \frac{1}{(1 + i)^n}\)
So, we have:
\(a + a^2 = 1\)
Equate to 0
\(a + a^2 - 1= 0\)
\(a^2 + a - 1= 0\)
Using quadratic formula:
\(a = \frac{-B \± \sqrt{B^2 -4AC}}{2A}\)
Where A=1; B =1 and C = -1
\(a = \frac{-1 \± \sqrt{1^2 -4 * 1 * -1}}{2 * 1}\)
\(a = \frac{-1 \± \sqrt{1 +4}}{2 }\)
\(a = \frac{-1 \± \sqrt{5}}{2 }\)
Recall that:
\(a = \frac{1}{(1 + i)^n}\)
So, we have:
\(\frac{1}{(1 + i)^n} = \frac{-1 \± \sqrt{5}}{2 }\)
Invert both sides
\((1 + i)^n = \frac{2}{-1 \± \sqrt{5}}\)
Square both sides
\(((1 + i)^n)^2 = (\frac{2}{-1 \± \sqrt{5}})^2\)
\((1 + i)^{2n} = (\frac{2}{-1 \± \sqrt{5}})^2\)
\((1 + i)^{2n} = \frac{4}{(-1 \± \sqrt{5})^2}\)
HELP PLEAASE I AM GOING TO EXPLODE WITH SAD WILL GIVE BRAINLIEST

Answers
Answer:D
Step-by-step explanation:i don’t know I’m guessing
3
2
1
-1
-2
-3
Determine the period.
2
4
6
8
10 12 14

Answers
The calculated period of the function is 12
How to determine the period of the functionFrom the question, we have the following parameters that can be used in our computation:
The graph
By definition, the period of the function is calculated as
Period = Difference between cycles or the length of one complete cycle
Using the above as a guide, we have the following:
Period = 13 - 1
Evaluate
Period = 12
Hence, the period of the function is 12
Rad more about period at
brainly.com/question/32322832
#SPJ1
Tim bought 2.7 pounds of potatoes and 1.9 pounds of carrots. How many pounds of vegetables did he buy in all
Answers
Hello!
The answer is 4.6 pounds!
You better believe it! :D
Answer:
4.6 pounds of vegetables.
Step-by-step explanation:
2.7 + 19 = 4.6 pounds.
what is the most effluence first step to isolate the variable term on one side of this equation -9x=-4x+5
Answers
what is the solution to the trigonometric inequality 2sin(x)+3>sin ^2(x) over the interval
Answers
The intervals that satisfy the given trigonometric Inequality are; 0 ≤ x < 3π/2 and 3π/2 < x ≤ 2π
How to solve trigonometric inequality?We are given the trigonometric Inequality;
2 sin(x) + 3 > sin²(x)
Rearranging gives us;
sin²(x) - 2 sin(x) - 3 < 0
Factorizing this gives us;
(sin(x) - 3)(sin(x) + 1) < 0
Thus;
sin(x) - 3 = 0 or sin(x) + 1 = 0
sin(x) = 3 or sin(x) = -1
sin(x) = 3 is not possible because sin(x) ≤ 1.
Thus, we will work with;
sin(x) = -1 for the interval 0 ≤ x ≤ 2π radians.
Then, x = sin⁻¹(-1)
x = 3π/2.
Now, if we split up the solution domain into two intervals, we have;
from 0 ≤ x < 3π/2, at x = 0. Then;
sin²(0) - 2 sin(0) - 3
= 0² - 0 - 3
= -3 < 0
Thus, the interval 0 ≤ x < 3π/2 is true.
From 3π/2 < x ≤ 2π, take x = 2π. Then;
sin²(2π) - 2 sin(2π) - 3
= 0² - 0 - 3
= -3 < 0
Thus, the interval 3π/2 < x ≤ 2π is also true.
Read more about trigonometric inequality at; https://brainly.com/question/27862380
#SPJ1
Name:
Write a system of equations and solve. Show all steps.
How many pounds of peanuts selling for 85 cents per pound must be mixed with 40 pounds of peanuts selling
for 98 cents per pound to produce a blend selling for 90 cents per pound?
Answers
Step-by-step explanation:
Let X be the number of pounds of peanuts selling for 85 cents per pound and Y be the number of pounds of peanuts selling for 98 cents per pound.
We can set up the following system of equations to represent this situation:
X * 0.85 + Y * 0.98 = 0.90 * (X + Y)
X + Y = 40
The first equation represents the total cost of the blend, and the second equation represents the total number of pounds of peanuts.
To solve this system of equations, we can use a method such as graphing, substitution, or elimination.
Using the substitution method, we can solve for one variable in terms of the other and substitute it into the other equation. For example, we can solve the first equation for X:
X = (0.90 * (X + Y) - Y * 0.98) / 0.85
Then, we can substitute this expression for X into the second equation:
(0.90 * (X + Y) - Y * 0.98) / 0.85 + Y = 40
Solving this equation for Y gives us the number of pounds of peanuts selling for 98 cents per pound:
Y = (40 * 0.85 - 0.90 * X) / (0.10 - 0.98)
To find the value of X, we can substitute this expression for Y into the first equation and solve for X:
X * 0.85 + (40 * 0.85 - 0.90 * X) / (0.10 - 0.98) * 0.98 = 0.90 * (X + (40 * 0.85 - 0.90 * X) / (0.10 - 0.98))
Solving this equation for X gives us the number of pounds of peanuts selling for 85 cents per pound:
X = 18.75
Therefore, 18.75 pounds of peanuts selling for 85 cents per pound must be mixed with 40 pounds of peanuts selling for 98 cents per pound to produce a blend selling for 90 cents per pound.
How do I subtract decimals from whole numbers?
Answers
Answer:
Just use long subtraction by expanding the decimal places of the whole number. This is done by adding a point, and enough zeros to it to match the number of decimal digits in the other number (digits after the decimal point).
12345678
i.e: 5 - 2.48374827, 2.48374827 has 8 decimal digits, so add 8 zeros after the point.
=
1 1 1 1 1 1 1
5.00000000
-
2.48374827
_______________
2.51625173
7 + 3 = 10, 7 + 2 + 1 = 10, 8 + 1 + 1= 10, 5 + 4 + 1 = 10, 2 + 7 + 1 = 10, 3 + 6 + 1 = 10, 1 + 8 + 1 = 10, 5 + 4 + 1 = 10, 2 + 2 + 1 = 5 : 5.00000000
This is basically borrowing a group of 10s which are the same as 1s in the next decimal place up.
For each digit except the first to the right, let 10 subtract that number from it and minus 1 since the 1 is carried over.
Matrix M has x-rows and (11-x) columns. Matrix N has y-rows and (y+5) columns. If MN and NM both are defined, find the values of x and y
Answers
Answer:
\(x=8, y=3\)
Step-by-step explanation:
Recall that if a matrix multiplication of two matrices is defined, then the number of columns of the first matrix is equivalent to the number of rows of the second matrix.
Since matrix M has (11-x) columns and matrix N has y rows, and MN is defined, so it follows:
\(y=11-x----(1)\)
Since matrix N has (y+5) columns and matrix M has x rows, and NM is defined, so it follows:
\(y+5=x----(2)\)
Substitute (1) into (2):
\(11-x+5=x\\2x=16\\\therefore x=8--(3)\)
Substitute (3) into (1):
\(y=11-8=3\)