Suppose you have $50 in a savings account and deposit an additional $10 each week.
a) Write a recursive formula to represent the sequence.
b) Write an explicit formula to represent the sequence.
c) How much money do you have in savings after 26
weeks? Show all work.​

Answer:

Option A

Step-by-step explanation:

Option A is an arithmetic sequence.

Each week, the salary goes up by a fixed $50.

To verify this, subtract any two consecutive weeks' salaries.

For example: $250 - $200 = $50; $350 - $300 = $50, etc.

The common difference in 50.

We have an arithmetic sequence with 20 terms. The first term is $200. We need to find the sum of the 20 terms.

The sum of an arithmetic sequence is given by the formula:

\( S_n = \dfrac{n}{2} \times [2a_1 + (n - 1)d] \)

S_n = sum of first n terms

n = number of terms = 20

a_1 = first term = 200

d = common difference = 50

\( S_{20} = \dfrac{20}{2} \times [2(200) + (20 - 1)(50)] \)

\( S_{20} = 10 \times [400 + 19(50)] \)

\( S_{20} = 10 \times [400 + 19(50)] \)

\( S_{20} = 13500 \)

Option A gives a total of $13,500 for the first 20 weeks.

Option B is a geometric sequence in which the salary goes up by 10% each week. To verify this, divide any salary by the previous week's salary.

For example: $220/$200 = 1.10; $266.20/$242 = 1.10; in each case, each salary is 1.1 times the previous week's salary which means a 10% increase. The common ratio of the geometric sequence is 1.1.

We need the formula for the sum of the first n terms of a geometric sequence.

\( S_n = \dfrac{a_1(1 - r^n)}{1 - r} \)

\( S_{20} = \dfrac{200(1 - 1.1^{20})}{1 - 1.1} \)

\( S_{20} = \dfrac{200(1 - 6.7274999)}{-0.1} \)

\( S_{20} = 11455 \)

Option B gives a total of $11,455 for the first 20 weeks.

Answer: Option A

Answer:

\(P(x>1)=0.9927\)

Step-by-step explanation:

From the question we are told that:

Mean \(\=x =7\)

Generally the Poisson equation for \=x is mathematically given by

\(P(x>1)=1-P(x \leq 1)\)

Therefor

\(P(x>1)=1-(\frac{e^{-7}*7^0}{0!}+{\frac{e^{-7}*7^1}{1!})\)

\(P(x>1)=1-(9.1*10^{-4}+6.3*10^{-3})\)

\(P(x>1)=1-(7.3*10^{-3}\)

\(P(x>1)=0.9927\)

The transformation function can be represented as vwxyz \($\rightarrow$\)qrstu = (v,w,x,y,z) \($\rightarrow$\) (q,r,s,t,u).

This algebraic representation of the transformation of pentagon vwxyz into pentagon qrstu is using the notation of a function. A function takes an input (in this case, the coordinates of pentagon vwxyz) and produces an output (in this case, the coordinates of pentagon qrstu). This transformation can be represented by the notation (v,w,x,y,z) \($\rightarrow$\) (q,r,s,t,u). This notation means that the coordinates (v,w,x,y,z) are being transformed into the coordinates (q,r,s,t,u). This notation is a concise way of expressing the transformation of pentagon vwxyz into pentagon qrstu. It is important to note that the transformation itself is not specified; the notation is simply used as a way of representing the transformation.

Learn more about function here

https://brainly.com/question/29633660

#SPJ4

Answer:

27.551%

Step-by-step explanation:

based on the given conditions ,formulate:

(1000x1.25-980)divide by 980

calculate the product or quotient :

1250 - 980 over 980 calculate the sum which would be 270 over 980

we gon cross out the common factor 27 over 98

rewrite the fraction as a decimal = 0.27551

multiply a number to both the numeration and denominator : 0.27551 x 100 over 100

now write as a single fraction  0.27551 x 100 / 100

calculate the product = 27.551 over 100

rewrite the fraction with denominator equals 100 to a presantage = 27.551

Answer: Duno

Step-by-step explanation:

Answer:

$ 0.75 for one pen

$1.05 per notebook

Step-by-step explanation:

John and Ariana bought school supplies. John spent $10.30 on 5 notebooks and 7 pens. Ariana spent $7.20 on 4 notebooks and 4 pens. What is the cost of 1 notebook and what is the cost of 1 pen?

John: 5n + 7p = 10.5

let's solve for n:

5n + 7p = 10.5

subtract 7p from both sides:

5n + 7p -7p = 10.5 - 7p

5n = 10.5 - 7p

divide both sides by 5:

5n/5 = (10.5 - 7p)/5

n = 2.1 - 7/5 p

Ariana: 4n + 4p = 7.20

Let's substitute in: n = 2.1 - 7/5 p

4n + 4p = 7.20

4(2.1 - 7/5p) + 4p = 7.20

multiply left side:

8.4 - 5.6p + 4p = 7.2

subtract 8.4 from both sides:

8.4 - 5.6p + 4p - 8.4 = 7.2 - 8.4

- 5.6p + 4p = -1.2

combine p terms on left side:

-1.6p = -1.2

divide both sides by -1.6:

-1.6p/(-1.6) = -1.2/(-1.6)

p = 0.75 cents for one pen

Now solve to find the price of a notebook:

4n + 4p = 7.20 when p = 0.75

4n + 4(0.75) = 7.20

4n + 3 = 7.20

subtract 3 from both sides:

4n + 3 - 3 = 7.20 - 3

4n = 4.2

divide both sides by 4:

4n/4 = 4.2/4

n = 1.05 per notebook

CHECK: when n = 1,05 and p = 0.75

John: 5n + 7p = 10.5

5(1.05) + 7(0.75) = 10.5

10.5 = 10.5

Ariana: 4n + 4p = 7.20

4n + 4p = 7.20

4(1.05) + 4(0.75) = 7.20

7.2 = 7.2

Answer assumes no additional sales tax.

\((f\circ g)(2)=\dfrac{1}{4\cdot2+9}=\dfrac{1}{17}\\\\(f+g)(2)=\dfrac{1}{2}+4\cdot2+9=\dfrac{1}{2}+17=\dfrac{1}{2}+\dfrac{34}{2}=\dfrac{35}{2}\)

answer: the range is 41.

to find the range of this data set, we first need to find the minimum and maximum values - which are 59 and 100.

then we subtract the minimum from the maximum.

59 - 100 = 41.

+(-11) is -11. You're "adding" -11 when in reality you're taking away 11 unless:

the equation looks like: -6+(-11)

the answer would be -17 because you're adding a negative to a negative. Taking away from a negative number is simply moving further down the negative number line, which makes the negative numbers "increase" in value

But if an equation looks like: 6+(-11)

the answer would be -5 since you are taking away 11 from a positive number.

Hope this makes sense and answers your question.

Answer:

The pvalue of the test is 0.3844 > 0.1, which means that there is not sufficient evidence at the 0.10 level to support the executive's claim

Step-by-step explanation:

A publisher reports that 35% of their readers own a laptop.

This means that the null hypothesis is:

\(H_0: p = 0.35\)

A marketing executive wants to test the claim that the percentage is actually different from the reported percentage.

This means that the alternate hypothesis is:

\(H_{a}: p \neq 0.35\)

The test statistic is:

\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)

In which X is the sample mean, \(\mu\) is the value tested at the null hypothesis, \(\sigma\) is the standard deviation and n is the size of the sample.

0.35 is tested at the null hypothesis:

This means that \(\mu = 0.35, \sigma = \sqrt{0.35*0.65}\)

A random sample of 190 found that 32% of the readers owned a laptop.

This means that \(X = 0.32, n = 190\)

Z-statistic:

\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)

\(z = \frac{0.32 - 0.35}{\frac{\sqrt{0.35*0.65}}{\sqrt{190}}}\)

\(z = -0.87\)

pvalue of the test and decision:

As we are testing that the mean is different from a value and z is negative, the pvalue of the test is 2 multiplied by the pvalue of z = -0.87

Looking at the z-table, z = -0.87 has a pvalue of 0.1922

2*0.1922 = 0.3844

0.3844 > 0.1, which means that there is not sufficient evidence at the 0.10 level to support the executive's claim

1. The velocity of the object is 3 m/s.

2. The object is moving in positive direction.

3. The total distance travelled is 5√10.

1. The velocity of the object is

= displacement / time

= 12/ 4

= 3 m/s

2. The object is moving in positive direction.

3. The total distance travelled

= √225+ 25

= √250

= 5√10

4. The displacement is

= 1/2 x base x height

= 1/2 x 5 x 15

= 37.5 m

Learn more about velocity here:

https://brainly.com/question/30559316

#SPJ1

Answer:

hello your question is incomplete attached below is the complete question

answer : 2/13    6/13

               6/13    3/13

Step-by-step explanation:

Firstly we will calculate the orthogonal basis L in R^2

attached below is the detailed solution

also assuming β to be the standard ordered basis

hence the matrix A of the reflection in the Line L in R2 =

2/13    6/13

6/13    3/13

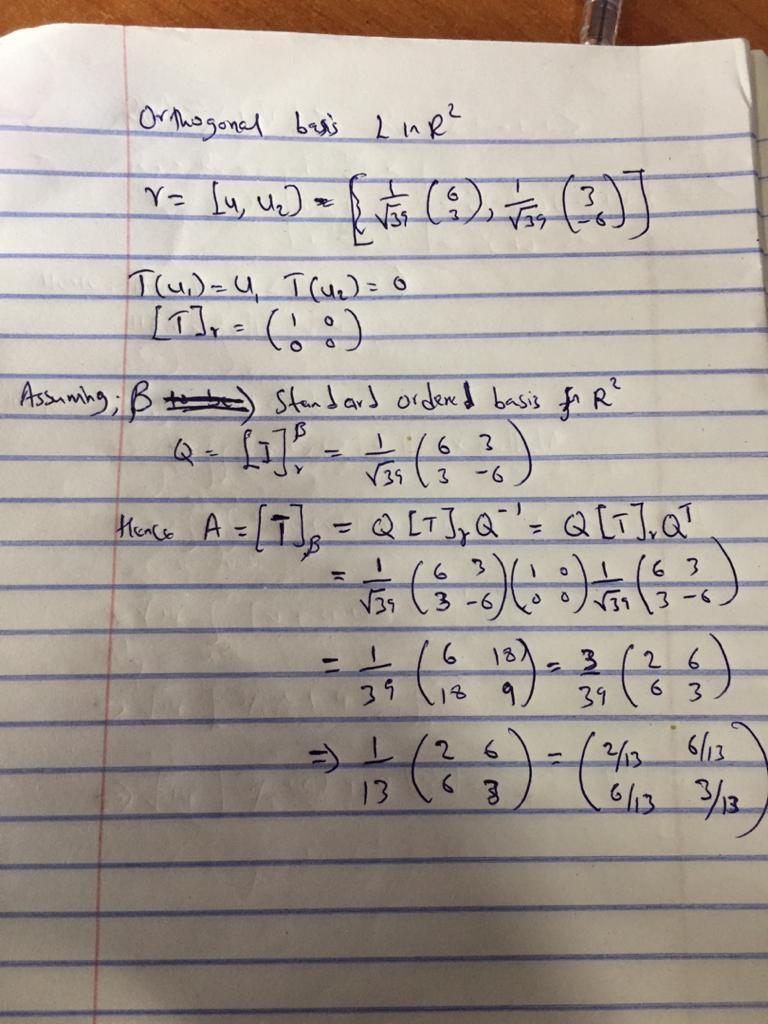
The matrix A of the reflection in line L is given by  \(\rm A = \begin{bmatrix}\dfrac{2}{13} & \dfrac{6}{13}\\ \dfrac{6}{13} & \dfrac{3}{13}\end{bmatrix}\)  and this can be determined by first evaluating the value of \(\rm R^2\) by using the given data.

The orthogonal basis L in \(\rm R^2\) is given by:

\(r = [u_1,u_2] =\left[\dfrac{1}{\sqrt{39} }\binom{6}{3}, \dfrac{1}{\sqrt{39} }\binom{3}{-6}\right]\)

\(\rm T(u_1)=u_1\)

\(\rm T(u_2)=0\)

\(\rm [T]_r = \begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix}\)

\(\rm Q = \dfrac{1}{\sqrt{39} }\begin{bmatrix}6 & 3\\ 3 & -6\end{bmatrix}\)

Now, matrix A is given by the formula:

\(\rm A=Q[T]_rQ^{-1}\)

Now, substitute the value of known terms in the above equation.

\(\rm A = \dfrac{1}{\sqrt{39} }\begin{bmatrix}6 & 3\\ 3 & -6\end{bmatrix}\begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix}\dfrac{1}{\sqrt{39} }\begin{bmatrix}6 & 3\\ 3 & -6\end{bmatrix}\)

Simplify the above expression.

\(\rm A = \dfrac{1}{{39} }\begin{bmatrix}6 & 18\\ 18 & 9\end{bmatrix}\)

\(\rm A = \dfrac{3}{{39} }\begin{bmatrix}2 & 6\\ 6 & 3\end{bmatrix}\)

\(\rm A = \dfrac{1}{{13} }\begin{bmatrix}2 & 6\\ 6 & 3\end{bmatrix}\)

Multiply by 1/13 in the matrix.

\(\rm A = \begin{bmatrix}\dfrac{2}{13} & \dfrac{6}{13}\\ \dfrac{6}{13} & \dfrac{3}{13}\end{bmatrix}\)

For more information, refer to the link given below:

https://brainly.com/question/16850761

Answer : 8$

you have 1$ left

Answer:

-13

Step-by-step explanation:

-b + 5c =

= -3 + 5(-2)

= -3 - 10

= -13

Answer: Technically its π (pie) 4

Step-by-step explanation:

If tan (x)=1 , then sin x = cos x . We know this is true for x=π4 as a base case. p = nπ , where n is an integer. The first positive value x0 for which tanx=1 is, as stated before, π4 . yw.

\(\textit{volume of a cylinder}\\\\ V=\pi r^2 h~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ r=5\\ h=3 \end{cases}\implies V=\pi (5)^2(3)\implies V\approx 236~ft^3\)

Answer:

236 ft^3

Step-by-step explanation:

Base radius = 5 ft

Height = 3 ft

Volume =   πr^2h

              =  π × 5^2 × 3

              =  75π

               =  235.61944901923 feet^3

Nearest Cubic Foot = 236 ft^3

Nearest Cubic Foot:

Hence Answer is:

236 ft^3

Hope this helps!

The value x in the secant line using the Intersecting theorem is 4.

Intersecting secants theorem states that " If two secant line segments are drawn to a circle from an exterior point, then the product of the measures of one of secant line segment and its external secant line segment is the same or equal to the product of the measures of the other secant line segment and its external line secant segment.

From the figure:

First sectant line segment = ( x - 1 ) + 5

External line segment of the first secant line = 5

Second sectant line segment = ( x + 2 ) + 4

External line segment of the second secant line = 4

Using the Intersecting secants theorem:

5( ( x - 1 ) + 5 ) = 4( ( x + 2 ) + 4 )

Solve for x:

5( x - 1 + 5 ) = 4( x + 2 + 4 )

5( x + 4 ) = 4( x + 6 )

5x + 20 = 4x + 24

5x - 4x = 24 - 20

x = 4

Therefore, the value of x is 4.

Option C) 4 is the correct answer.

Learn more about Intersecting secants theorem here: brainly.com/question/30242636

#SPJ1

Answer:

86.6

The quotient is the final answer

Step-by-step explanation:

(780/9) = quotient ( 86.66)

Answer:

86.6

Step-by-step explanation:

Answer:

7

Step-by-step explanation:

7x7=49+5=54

Answer:

y = 7

Step-by-step explanation:

Alrighty, here we go!

First step is to subtract 5 from 5 and from 54. Cancel out the 5's.

After doing so, you have 7y = 49.

Now, divide 7 from 7y and from 49. Cancel out the 7's.

Now you have y = 7

There is your answer!

Mark brainliest if possible please :)

The rate of change of the area of the trapezoid at that instant is 5 square kilometers per second and this can be determined by differentiating the area of the trapezoid with respect to time 't'.

Given :

First, determine the area of a trapezoid, that is:

\(\rm A = \dfrac{b_1+b_2}{2}\times h\)

\(\rm \dfrac{2A}{h}=b_1+b_2\)

\(\rm b_2 = \dfrac{2A}{h}-b_1\)

Now, differentiate the above expression with respect to 't'.

\(\rm \dfrac{db_2}{dt} = -\dfrac{2A}{h^2}\dfrac{dh}{dt}-\dfrac{db_1}{dt}\)

Now. substitute the values of the known terms in the above formula.

\(\rm \dfrac{db_2}{dt} = -\dfrac{2\times (16)}{2^2}\times (5)-(-8)\)

\(\rm \dfrac{db_2}{dt} = -32\;km/sec\)

So, the area is decreasing at the rate of 5.

For more information, refer to the link given below:

https://brainly.com/question/1083374

Answer:

1 foot squared

Step-by-step explanation:

Er... a square foot is 1 foot squared

The equivalent value to 2.76 is C. two and nineteen twenty-fifths.

An equivalent value is an amount or numerical expression possessing the same value as the other.

Equivalent values are expressed as equations, using the equation symbol (=).

Equations are a class of the properties of mathematical expressions, including numbers and variables.

Two and nineteen twenty-fifths = 2¹⁹/₂₅.

When expressed as a decimal, 2¹⁹/₂₅ = 2.76.

Thus, 2.76%, 27.6%, or twenty-five over nineteen are not equivalent values of 2.76 but 2¹⁹/₂₅.

Learn more about equivalent values at https://brainly.com/question/843074

#SPJ1

Answer:

Step-by-step explanation:

First the max degree is 360

Then multiply by 5/8

360 x 5/8 = 1800/8

1800/8 = 225

Answer: 225

When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.

The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.

Replacing x with 1, we have:

ƒ(1) = -4(1) - 5

Simplifying further:

ƒ(1) = -4 - 5

ƒ(1) = -9

Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.

Let's break down the steps taken to arrive at the solution:

1. Start with the function f(x) = -4x - 5.

2. Replace x with 1 in the function.

3. Evaluate the expression by performing the necessary operations.

4. Simplify the expression to obtain the final result.

In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.

It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.

Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.

For more questions on Function .

https://brainly.com/question/11624077

#SPJ8

Answer:

y = x + 8

General Formulas and Concepts:

Algebra I

Step-by-step explanation:

Step 1: Define

Standard Form: x - y = -8

Step 2: Rewrite

Find slope-intercept form

Answer:

2 1/3 or 2.33

Step-by-step explanation:

The equivalent value of the fraction is A = 7/3

An element of a whole is a fraction. The number is represented mathematically as a quotient, where the numerator and denominator are split. Both are integers in a simple fraction. A fraction appears in the numerator or denominator of a complex fraction. The numerator of a proper fraction is less than the denominator.

Given data ,

Let the fraction be represented as A

Now , the value of A is

Let the first number be p = 7

Let the second number be q = 1/3

And , A = pq

A = 7 ( 1/3 )

A = 7/3

Hence , the fraction is A = 7/3

To learn more about fractions click :

https://brainly.com/question/29766013

#SPJ2

The resulting equation after multiplying the first equation by 2 and subtracting the second equation is:

-5y = -375

1. Given equations:

  - x + 3y = 350    (Equation 1)

  - 2x + 4y = 625   (Equation 2)

2. Multiply Equation 1 by 2:

  - 2(x + 3y) = 2(350)

  - 2x + 6y = 700    (Equation 3)

3. Subtract Equation 2 from Equation 3:

  - (2x + 6y) - (2x + 4y) = 700 - 625

  - 2x - 2x + 6y - 4y = 75

  - 2y = 75

4. Simplify Equation 4:

  -2y = 75

5. To isolate the variable y, divide both sides of Equation 5 by -2:

  y = 75 / -2

  y = -37.5

6. Therefore, the resulting equation is:

  -5y = -375

For more such questions on multiplying, click on:

https://brainly.com/question/29793687

#SPJ8

Answer:

2197 cm³

Step-by-step explanation:

surface area of cuboid = 2 * (5*9 + 33*9 + 33*5) = 1014

surface area of cube = 6 * x²   .... x: side length of cube

6x² = 1014

x² = 169

x = 13

volume of cube = x³ = 13³ = 2197 cm³