Pls help I really need it ASAP

Answer:

Step-by-step explanation:

Area of the rectangle length x width

7.5x5.3 =39.75 sq.m

so, B is the correct answer.

The 15,25 feet width of the sheet metal gives a drain that has a maximum cross-sectional area of approximately, 29.07 square feet. The width of the drain that has the maximum cross sectional area is 7.625 feet, and the depth of the drain is 3.8125 feet.

The dimensions of an open drain include the width and the depth of the drain.

The width of the sheet metal = 15.25 feet

Let x represent the depth of the drain. The width, w, of the drain is found from x as follows; w = 15.25 - 2·x

Area of a rectangle = Width × Height (or depth)

The area of the rectangular drain is therefore; A = w × x

Which gives; A = x × (15.25 - 2·x) = 15.25·x - 2·x²

Given that the coefficient of x² is negative, the maximum volume is given by the point at which the rate of change of the the area is zero as follows;

\(At \ the \ maximum \ volume, \ \dfrac{dA}{dx} = 0 = \dfrac{d}{dx} \left(15.25\cdot x - 2\cdot x^2\right) = 15.25 - 4\cdot x\)

At the point where the volume is maximum, we have;

\(x = \dfrac{15.25}{4} = 3.8125\)

The depth of the drainage that gives the maximum volume is x = 3.8125 feet

w = 15.25 - 2·x

Therefore;

w = 15.25 - 2×3.8125 = 7.625

The width of the drainage is, w = 7.625 feet

\(A_{max}\) = 15.25×3.8125 - 2×3.8125² ≈ 29.07

The area of the drain that gives the maximum area is, \(A_{max}\) = 29.07 ft²

The description of the drain that has the maximum cross sectional area are as follows;

Width; 7.625 feet

Depth; 3.8125 feet

Area; Approximately 29.07 ft.²

Learn more about the maximum value of a function here:

https://brainly.com/question/5722003

#SPJ1

Answer:

Because  a drop in temperature means decrease in temperature therefore, we take an integer  with negative sign and added to previous temperature.

Step-by-step explanation:

Drop in temperature means decrease in the temperature .When the temperature decreases then we take decrease value of temperature in negative integer. Because decrease means the temperature fall  down  .Hence , the  decrease in temperature measure with negative sign .

For example,  if we take temperature T= 70°C.

If the temperature decreases by 5°c  then the temperature

Decrease in temperature=-5°C

Hence, the temperature T= 70+(-5)=65°C.

Therefore , from example we can say that when temperature decreases by some value in integer . Then ,we get final  temperature obtained  by adding  drop in temperature ( negative integer  ) in previous value of the temperature.

Answer: Sample reasopnse

A drop in temperature means the temperature will decrease. That decrease is represented by a negative integer, which should be added to the previous temperature.

Step-by-step explanation:

Answer: Line DE

Step-by-step explanation:

Line DE doesn't show a correct way to label the line

Answer:

The 32-ounce box

Step-by-step explanation:

The 16-ounce box costs $3.20 for every 16 ounces, but the 32-ounce box costs $3.12 for every 16 ounces. That means the 32-ounce box is a better deal by 8 cents.

Answer:

the big box is a better buy

Step-by-step explanation:

we have

$3.20 for 16ounce

and notice 32 is duble of 16 so to be equal price will be

$6.40 for 32ounce

yet is not is

$6.24 for 32ounce so the big box is less expensive

Answer:

all real values

Step-by-step explanation:

the domain is the possible input values

The domain is all real values since we can put in any value for x

Answer:

A) All Real Numbers

Step-by-step explanation:

Just is

Answer:

H equals 24

24/4 equals 6

Answer:

h = 24

Step-by-step explanation:

multiply both sides

h/4=6

4 x h/4 = 4 x 6

reduce multiply

and the solution is h = 24

A sample is a subset of the population. When conducting a survey, it is often impractical to gather data from every member of a population, and therefore, a sample is used. The goal of a sample is to gather data that is representative of the population. In the case of the instructional designer, they would need to identify the population of learners they are interested in (e.g. learners enrolled in their course) and take a sample of those learners to estimate the proportion who use Firefox as their primary browser.

There are various sampling procedures that can be used, but the most common is simple random sampling. In simple random sampling, each member of the population has an equal chance of being selected for the sample. The instructional designer could use a random number generator or a table of random numbers to select their sample of learners. Once they have their sample, they can count the number of learners who use Firefox as their primary browser and use this proportion to estimate the proportion in the population.

To know more about conducting visit :-

https://brainly.com/question/31201773

#SPJ11

\( \: \: \: \: 15.5 \\ - 11.2 \)

ANSWER :-

4.3

Answer: y=1/2x-3

Step-by-step explanation:

I'm assuming you're trying to find it in slope intercept form!

y=mx+b

y=1/2x-3

easy

Answer:

Answer:

a. 9

b. The slope represents the cost for every new DVD

c. 6

d. The song represents the base price, or the price that it would cost for 0 DVDs

e. y = 9x + 6

Explanation:

I made a graph on a piece of graph paper and these were the answer I got.

The perimeter of ΔNOP is equal to 25.6 units.

In Mathematics, the basic proportionality theorem states that when any of the two (2) sides of a triangle is intersected by a straight line which is parallel to the third (3rd) side of the triangle, then, the two (2) sides that are intersected would be divided proportionally and in the same ratio.

By applying the basic proportionality theorem to the given triangles, we have the following:

ΔNOP ≅ ΔKLM

OP/ML = x/KL

x = (OP × KL)/ML

x = (8 × 7)/5

x = ON = 11.2 units.

For the perimeter of ΔNOP, we have;

Perimeter of ΔNOP = OP + NP + ON

Perimeter of ΔNOP = 8 + 6.4 + 11.2

Perimeter of ΔNOP = 25.6 units.

Read more on basic proportionality theorem here: brainly.com/question/3213812

#SPJ1

Answer:

Value of Cos 120 is -½.

Step-by-step explanation:

The sumerian mathematical system was based on units of sixty, ten, and six and survives in what modern system time measurement.

Sumer (a region of Mesopotamia, present-day Iraq) is sometimes referred to as the Cradle of Civilization because it was the origin of writing, the wheel, agriculture, the arch, the plow, irrigation, and many other accomplishments.

We really know more about ancient Sumerian and Babylonian mathematics than we do about early Egyptian mathematics because the Sumerians invented the first known writing system, the pictographic cuneiform script, which uses wedge-shaped symbols engraved on baked clay tablets. In fact, we even have math and geometry problems that seem like school exercises.

The base number 60 was created by adding a "celestial" 6 and a "common" 10 in the Sumerian "sexagesimal" system.

To learn more about sumerian mathematical system from given link

https://brainly.com/question/5659298

#SPJ4

The geometric mean radius of the unconventional conductors in terms of the radius r of an individual strand is 1.583r.

To find the geometric mean radius of the unconventional conductors, we need to understand the concept of geometric mean. The geometric mean of two numbers is the square root of their product. In this case, we are looking for the geometric mean radius of multiple strands.

First, we need to determine the number of strands in the unconventional conductors. The question does not provide this information explicitly, so we assume there are at least two strands.

We know that the geometric mean radius is the square root of the product of the individual strand radii. Let's assume there are n strands, and the radius of each strand is r. Therefore, the product of the individual strand radii would be r^n.

Now, we can calculate the geometric mean radius by taking the square root of r^n. Mathematically, it can be expressed as (r^n)^(1/n) = r^((n/n)^(1/n)) = r^1 = r.

Therefore, the geometric mean radius in terms of the radius r of an individual strand is 1.583r.

Learn more about

#SPJ11

Answer:

look for this i use socratic it tells you the work

Answer:

Questions 1. 10=x-15

step 10=x-15

switch sides x-15=10

add 15 to both sides

x-15+15=10+15

answer

simply x=25

Sasha should use 2 desired outcomes in her probability calculation to determine that she has a 1/3 chance of winning the game.

To calculate Sasha's probability of winning, we need to determine how many desired outcomes she has. In this game, Sasha needs to spin a number higher than both of her friends' spins, which means she needs to spin a number greater than 1 and 4.

Let's analyze the spinner pictured. From the image, we can see that the spinner has numbers ranging from 1 to 6. Since Sasha needs to spin a number higher than 4, she has two options: 5 or 6.

Now, let's consider the desired outcomes. Sasha has two desired outcomes, which are spinning a 5 or spinning a 6. If she spins either of these numbers, she will have a number higher than both of her friends and win the game.

To calculate Sasha's probability of winning, we need to divide the number of desired outcomes by the total number of possible outcomes. In this case, the total number of possible outcomes is the number of sections on the spinner, which is 6.

Sasha's probability of winning is 2 desired outcomes divided by 6 total outcomes, which simplifies to 1/3.

For more such questions on probability

https://brainly.com/question/251701

#SPJ8

.

Answer:13cm

Step-by-step explanation:

Answer:

Annalise is correct because the outputs are closest when x = 1.35

Step-by-step explanation:

The solution to the equation 1/(x-1) = x² + 1 means the one x value that will make both sides equal. If we look at the table, notice how when x = 1.35, f(x) values are closest to each other for both equations, signifying that x = 1.35 is approximately the solution. Thus, Annalise is correct.

First, notice that since we have an isosceles trapezoid, the base angles will be equal, then:

next, we have that the angles adjacent to opposite bases are supplementary, then we can write the following equation:

using the fact that the measure of angle 3 is 60 degrees, we can find the measure of angle 2:

then, since angles 1 and 2 are also base angles, they are equal. Therefore, the measure of the anlges is:

Answer:

A

Step-by-step explanation:

a) ✔️

This is the principle of mathematical induction. If P holds for the base case k=1 and we can show that if it holds for any arbitrary k (e.g. k=n) then it must also hold for the next value (e.g. k=n+1), then we have shown it holds for all natural numbers.

b) ❌

There is no guarantee that P holds for all natural numbers from the statement alone. It only guarantees that for any k where P does not hold, there exists a smaller number i where P does not hold.

c) ❌

This is the principle of weak mathematical induction. It only shows that if P holds for a given k and for all smaller values i then it must hold for k+1. It does not guarantee that P holds for all natural numbers.

d) ❌

This statement is the negation of the principle of mathematical induction. It is known as the "strong induction" principle, which assumes that if P does not hold for k, then there exists a smaller i where P does not hold. However, this principle is not sufficient to prove that P holds for all natural numbers k.

Answer:

66

Step-by-step explanation:

180 - 114)  These angles are supplemental.  They add to 180

66

Answer:

m<6=66°

Step-by-step explanation:

Because m<2 and m<3 are both on a straight line, we know they must add to 180°:

m<2 + m<3 =180

We know m<3=114°, so:

m<2 +114 = 180

m<2 = 66

Since AB|CD, m<2 and m<6 are corresponding angels, making them equal, and so m<6=66°.

Answer:

20

Step-by-step explanation:

Answer:

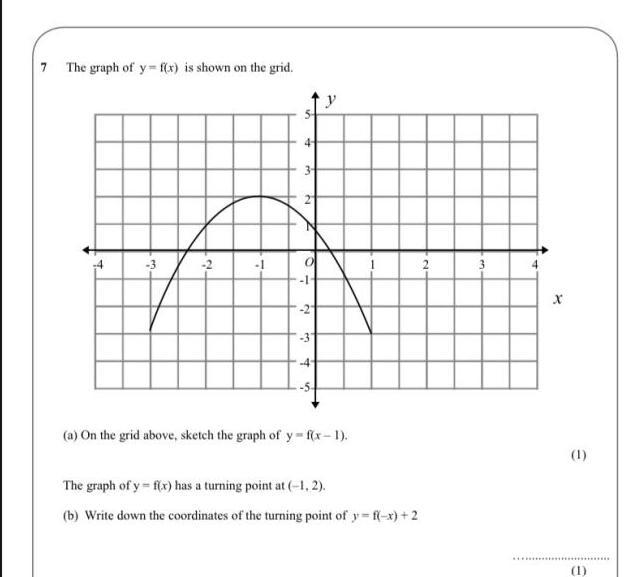
the turning point is (-1,2)

Step-by-step explanation:

Darwin's geometric ratio of increase pertains specifically to the growth rate of populations in biological organisms. According to Darwin's theory of evolution, populations have the potential to increase exponentially over time if certain conditions are met. The geometric ratio of increase, often denoted as "r" or the intrinsic rate of natural increase, represents the factor by which a population multiplies during each reproductive cycle or generation.

In the context of natural selection, individuals with higher reproductive rates (higher r-values) have a greater chance of passing on their genetic traits to the next generation. Over time, this can lead to significant population growth and evolutionary changes within a species. However, the geometric ratio of increase is limited by various factors, such as availability of resources, competition, predation, and environmental constraints, which can result in a balance between population growth and environmental carrying capacity.

To learn more about organisms : brainly.com/question/13278945

#SPJ11

Area of the isosceles triangle is 29/2 when the points of the triangle are (-3,-1), (1, -1),(-1,4).

Given that,

The point of the triangle are (-3,-1), (1, -1),(-1,4).

We must calculate the isosceles triangle's area.

We know that,

Take the points as

A(-3,-1), B(1, -1), C(-1,4).

We have to first find the distance from points.

Distance formula is square root of (x₂-x₁)²+(y₂-y₁)²

AB= √(1+3)²+(-1+1)² = √4²+0²=√4²=4

BC= √(-1-1)²+(4+1)² = √-2²+5²=√4+25=√29

CA= √(-3+1)²+(-1-4)² = √-2²+-5²=√4+25=√29

The area of the triangle is half into base into height

=1/2×b×h

=1/2×√29×√29

=1/2×29

=29/2

Therefore, Area of the isosceles triangle is 29/2 when the points of the triangle are (-3,-1), (1, -1),(-1,4).

To learn more about triangle visit: https://brainly.com/question/2773823

#SPJ9

Answer:

n > 5

Step-by-step explanation:

Answer:

3n + 2 > 17

Step-by-step explanation:

3n + 2 > 17

-2 -2

3n > 15

÷3 ÷3

n > 5

The first term, a1, in the geometric series is -3.

What is Geometric Series?

A geometric series is a series for which the ratio of two consecutive terms is a constant function of the summation index. The more general case of a ratio and a rational sum-index function produces a series called a hypergeometric series. For the simplest case of a ratio equal to a constant, the terms have the form

To find the first term, a1, in a geometric series given the sum, Sn = 93, the common ratio, r = 2, and the number of terms, n = 5, we can use the formula for the sum of a geometric series:

Sn = a1 * (1 - r^n) / (1 - r)

Plugging in the given values, we have:

93 = a1 * (1 - 2^5) / (1 - 2)

Simplifying the expression:

93 = a1 * (1 - 32) / (-1)

93 = a1 * (-31)

Now we can solve for a1 by dividing both sides of the equation by -31:

a1 = 93 / -31

a1 = -3

Therefore, the first term, a1, in the geometric series is -3.

To learn more about Geometric Series from the given link

https://brainly.in/question/13322627

#SPJ4

Answer:

-8.5

Step-by-step explanation:

\(\sqrt{-72}\) = -8.48528137424 = -8.5

Answer:

\({ \underline{ \mathfrak{ \: answer : }}}\)

• Note that in complex numbers, i² = -1

\({ \rm{ \sqrt{ - 72} = \sqrt{ - 1 \times (4 \times 9 \times 2)} }} \\ \\ = { \rm{ \sqrt{ - 1} \times \sqrt{4} \times \sqrt{9} \times \sqrt{2} }} \\ \\ = { \rm{ \sqrt{( {i}^{2} )} \times 2 \times 3 \times \sqrt{2} }} \\ \\ = { \rm{i \times 6 \times \sqrt{2} }} \\ \\ { \boxed{ \boxed{ \rm{ \: \: answer= { \rm{6i \sqrt{2} }}}}}}\)

a = amount invested at 7%

b = amount invested at 9%

we know the amount invested was ₹36000, thus we know that whatever "a" and "b" are, a + b = 36000.  We can also say that

\(\begin{array}{|c|ll} \cline{1-1} \textit{a\% of b}\\ \cline{1-1} \\ \left( \cfrac{a}{100} \right)\cdot b \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{7\% of a}}{\left( \cfrac{7}{100} \right)a}\implies 0.07a~\hfill \stackrel{\textit{9\% of b}}{\left( \cfrac{7}{100} \right)b}\implies 0.09b\)

since we know the interest earned from the invested was ₹2920, then we say that 0.07a + 0.09b = 2920.

\(\begin{cases} a + b = 36000\\\\ 0.07a+0.09b=2920 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{using the 1st equation}}{a + b = 36000\implies \underline{b = 36000-a}}~\hfill \stackrel{\textit{substituting on the 2nd equation}}{0.07a~~ + ~~0.09(\underline{36000-a})~~ = ~~2920} \\\\\\ 0.07a+3240-0.09a=2920\implies 3240-0.02a=2920\implies -0.02a=-320 \\\\\\ a=\cfrac{-320}{-0.02}\implies \boxed{a=16000}~\hfill \boxed{\stackrel{36000~~ - ~~16000}{20000=b}}\)