If a plane can travel 510 miles per hour with the wind and 410 miles per hour against the wind, find the speed of the wind and the speed of the plane in still air.
Answers
Answer:
Below.
Step-by-step explanation:
Ok so, Since its 510 - x = 410. Speeds equals the wind.
SO?
100=2x
x=50
410+50 = 460!
Related Questions
let be a trapezoid with parallel to and perpendicular to . let be a point on such that . if , and , what is the value of ?
Let ABCD be a trapezoid with BCǀǀAD and AB=BC=CD= ½ AD. What is ACD?
Answers
The value of ACD of a trapezium is 26.56°.
Let ABCD be a trapezoid with BCǀǀAD and AB=BC=CD= ½ AD.
ACD can be determined by using the Pythagorean theorem or using the theorem of Pythagoras.
The theorem of Pythagoras states that if you draw a right-angled triangle with the hypotenuse as c and the legs a and b.
The sum of squares of the legs (a and b) equals the square of the hypotenuse (c).
Therefore, by using the Pythagorean theorem ; AC² = AB² + BC²
=> AC² = (1/2 AD)² + (1/2 AD)²
=> AC² = 1/4 AD² + 1/4 AD²
=> AC² = 1/2 AD².
Hence,AC² = 1/2 AD²
ACD is a right-angled triangle where AC is the hypotenuse.
Thus, using the theorem of Pythagoras, we can write: AD² = AC² + CD²
=> AD² = [√(1/2 AD²)]² + (AD/2)²
=> AD² = 1/2 AD² + 1/4 AD²
=> AD² = 3/4 AD²=> AD = √4/3 AD
Thus, ACD=ACD = tan¯¹(√1/2 AD²/AD/2) = tan¯¹(√2/4) = 26.56°
Therefore, ACD is 26.56°.
To know more about "PYTHAGOREAN THEOREM" refer here:
https://brainly.com/question/343682#
#SPJ11
Divide.
(−14)÷(−34)
What is the quotient?
Enter your answer as a simplified fraction in the box.
Answers
Answer:
\( \frac{7}{17} \)
Step-by-step explanation:
(-14) ÷ (-34)
14/34
= ⁷/17
The quotient of the division will be 0.41. And the solution of the division (−14) by (−34) would be 7/17 as a simplified fraction.
How can we interpret the division?When 'a' is divided by 'b', then the result we get from the division is the part of 'a' that each one of 'b' items will get. Division, thus, can be interpreted as equally dividing the number that is being divided in total x parts, where x is the number of parts the given number is divided.
We need to divide the mixed fraction with integers, So
(-14) ÷ (-34)
The common denominator we can calculate as the least common multiple of the denominators then we get
14/34
= 7/ 17
= 0.41
Thus, the quotient of the division will be 0.41
Therefore, the solution of the division (−14) by (−34) would be 7/ 17 as a simplified fraction.
Learn more about division here:
brainly.com/question/26411682
#SPJ2
34.
16
7
200
Not drawn to scale
A. 24
B. 66
C. 69
D. 58
Answers
apply the distributive property to write an equivalent expression
4(2+w)
Answers
Find the particular solution that satisfies the differential equation and the initial condition. f''(x) = sinx.
Answers
The particular solution that satisfies the differential equation and the initial condition f(0) = a is: f(x) = -sin(x) + C1x + a.
To find the particular solution that satisfies the differential equation f''(x) = sin(x) and an initial condition, we need to integrate the equation twice and apply the initial condition.
1. First Integration:
Integrating the differential equation f''(x) = sin(x) with respect to x once gives us:
f'(x) = -cos(x) + C1
where C1 is the constant of integration.
2. Second Integration:
Integrating f'(x) = -cos(x) + C1 with respect to x again gives us:
f(x) = -sin(x) + C1x + C2
where C2 is another constant of integration.
3. Applying the Initial Condition:
To apply the initial condition, we need to use the given information about the problem. Let's say the initial condition is given as f(0) = a, where 'a' is a specific value.
Substituting x = 0 and f(x) = a into the equation, we get:
a = -sin(0) + C1(0) + C2
a = 0 + 0 + C2
C2 = a
Therefore, the particular solution that satisfies the differential equation and the initial condition f(0) = a is:
f(x) = -sin(x) + C1x + a
In this particular case, the initial condition f(0) = a determines the value of the constant C2, which becomes C2 = a. The resulting particular solution incorporates the constant C1 from the first integration and the constant a from the initial condition.
Note that without a specific initial condition or boundary condition, the constants C1 and C2 remain arbitrary and can be adjusted to fit different situations or additional information if provided.
for more such question on equation visit
https://brainly.com/question/17145398
#SPJ8
URGENT!! ILL GIVE
BRAINLIEST! AND 100 POINTS
Match the new coordinates
that define the figure after
dilation with a center at the
origin by the given scale factor

Answers
The new coordinates that define the figure after dilation with a center at the origin by the given scale factor are;
1) (1, 0)
2) (1, 4/3)
3) (0, 4/3)
4) (9/2, 0)
5) (9/2, 6)
6) (0, 6)
What are the coordinates of the dilation by a scale factor?When we dilate a shape or coordinate by a scale factor, it means that we are going to multiply the dimensions of the coordinates by that scale factor. Thus;
1) (3, 0) dilated by a scale factor of 1/3 is;
1/3 *3, 0 * 1/3 = (1, 0)
2) (3, 4) dilated by a scale factor of 1/3 is;
1/3 *3, 4 * 1/3 = (1, 4/3)
3) (0, 4) dilated by a scale factor of 1/3 is;
1/3 *0, 4 * 1/3 = (0, 4/3)
4) (3, 0) dilated by a scale factor of 3/2 is;
3 *3/2, 0 * 3/2 = (9/2, 0)
5) (3, 4) dilated by a scale factor of 3/2 is;
3 *3/2, 4 * 3/2 = (9/2, 6)
6) (0, 4) dilated by a scale factor of 3/2 is;
0 *3/2, 4 * 3/2 = (0, 6)
Read more about scale factor dilation at; https://brainly.com/question/10253650
#SPJ1
A party tent is used for an outdoor event. Ropes of equal length support each tent pole. The angle each rope makes with the ground is 52°.
What is the height of each tent pole?

Answers
Therefore, the height of each tent pole is approximately 8.07 meters.
What is trigonometry?Trigonometry is a branch of mathematics that deals with the study of the relationships between the sides and angles of triangles. It is used to solve problems involving triangles, such as finding the length of a side or the measure of an angle. Trigonometry is based on the use of trigonometric functions, which are ratios of the sides of a right triangle.
Here,
We can use trigonometry to solve this problem. Let's call the height of the tent pole "h" and the length of the rope "r". Then, we can use the tangent function to find the height:
tan(52°) = h/r
Rearranging this equation, we get:
h = r * tan(52°)
We know that the length of each rope is equal, so we can choose any arbitrary length for r. For simplicity, let's assume that each rope is 10 meters long. Then, we can plug in the values into the equation:
h = 10 * tan(52°)
Using a calculator, we get:
h ≈ 8.07 meters
To know more about trigonometry,
https://brainly.com/question/26719838
#SPJ1
i need help with this question please

Answers
Answer:
5x-30
Step-by-step explanation:
x+15+4x-45
5x+14-45
5x-30
Can someone Please help.. 1-22

Answers
Answer:
1. 2
2. 7
3. 17
4. 18
5. 83
6. 79
7. 7
8. 7
9. 19
10. 54
11. 26
12. 16
13. 9
14. 4
15. 3
16. 7
17. 5
18. 5
19. 30
20. 14
21. 20
22. 27
Step-by-step explanation:
Hope this helps!
The perimeter of square S is 40. Square T is inscribed in square S. What is the least possible value of the area of square T ?
A. 45
B. 48
C. 49
D. 50
E. 52
Answers
The least possible value of the area of square T is 49 i.e., the correct answer is option (C) 49, representing the least possible value of the area of square T.
The least possible value of the area of square T can be determined by analyzing the relationship between the two squares and their perimeters.
Let's denote the side length of square S as 'a'.
Since the perimeter of square S is 40, each side of the square has a length of 10 (40 divided by 4).
Square T is inscribed in square S, which means that its corners touch the sides of square S.
To find the least possible value of the area of square T, we need to consider the scenario where square T is the smallest possible square that can be inscribed in square S.
In this case, the sides of square T are parallel to the sides of square S, and the corners of square T coincide with the midpoints of the sides of square S.
Since square T is inscribed in square S, the diagonal of square T is equal to the side length of square S.
Using the expression of Pythagorean theorem, we can calculate the length of the diagonal of square T:
Diagonal of square T = √(\(10^2 + 10^2\)) = √200 = 10√2
The side length of square T can be found by dividing the diagonal length by √2:
Side length of square T = 10√2 / √2 = 10
Therefore, the area of square T is (side length)^2 = \(10^2\) = 100.
However, we are looking for the least possible value of the area of square T.
Since the answer choices are given, we can see that the smallest possible area is 49, which corresponds to option (C).
Hence, the correct answer is option (C) 49, representing the least possible value of the area of square T.
Learn more about Expression here:
https://brainly.com/question/11701178
#SPJ11
A survey found that the american family generates an average of 17. 2 pounds of glass garbage each year. Assume the standard deviation of the distriution is 2. 5 pounds. Find the probability that the mean of a sample of 55 families will be between 17 and 18 pounds
Answers
The probability that the mean of a sample of 55 families will be between 17 and 18 pounds is approximately 71.55%.
How to solve for the probabilityσ_sample = σ / sqrt(n)
σ_sample = 2.5 / sqrt(55)
σ_sample ≈ 0.336
Now, we can standardize the values of 17 and 18 pounds using the Z-score formula. This will tell us how many standard deviations away from the population mean these values are:
Z = (X - μ) / σ_sample
Z_17 = (17 - 17.2) / 0.336 ≈ -0.595
Z_18 = (18 - 17.2) / 0.336 ≈ 2.381
Now we will use the standard normal distribution (Z-distribution) to find the probabilities corresponding to these Z-scores. You can use a Z-table, statistical software, or an online calculator to find these probabilities.
P(Z < -0.595) = 0.2760
P(Z < 2.381) = 0.9915
To find the probability that the mean of a sample of 55 families will be between 17 and 18 pounds, we will find the difference between the probabilities corresponding to the two Z-scores:
P(17 < X < 18) = P(Z < 2.381) - P(Z < -0.595)
P(17 < X < 18) = 0.9915 - 0.2760
P(17 < X < 18) ≈ 0.7155
So, the probability that the mean of a sample of 55 families will be between 17 and 18 pounds is approximately 71.55%.
Read more on probability here:https://brainly.com/question/24756209
#SPJ4
Which expression is equivalent to

Answers
Answer:
\(\frac{(x+2)}{(x-1)}\)
Step-by-step explanation:
\(\frac{x^2 + x -2}{x^2 -2x+1}\) =
\(\frac{(x+2)(x-1)}{(x-2)(x-1)}\) =
\(\frac{(x+2)}{(x-1)}\)
point of the circumference

Answers
Answer:
(-14, 4)
Step-by-step explanation:
I graphed it on Desmos Graphing calculator. This is a great resource. Hope this helps!
Step-by-step explanation:
( - 14, -4)
is a right answer
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.
A fashion photographer needs to hire a stylist to prepare his models. Jayla charges $156 for showing up, plus $63 per hour. Sally charges $158 plus $62 per hour. The photographer realizes that, given the expected duration of his photo shoot, either stylist would cost him the same amount. What would the cost be? What would the duration be?
Either stylist would cost $ if the shoot lasted. hours
Answers
The duration of shoot would be 2 hours and Either stylist would cost $282 if the shoot lasted 2 hours.
A fashion photographer needs to hire a stylist to prepare his models.
Let the number of hours stylist take = x
Jayla charges $156 for showing up, plus $63 per hour. So, this can be mathematically written as ,
156 + 63x equation 1
Sally charges $158 plus $62 per hour. So, this can be mathematically written as ,
158 + 62x equation 2
As per the question, the expected duration of his photo shoot, either stylist would cost him the same amount. So we can equate equation 1 and equation 2. On equating equation 1 and equation 2 , we will get
156 + 63x = 158 + 62x
⇒ x = 2
So, the duration would be 2 hours.
Jayla cost = Sally cost = 156 + 63x = 156 + (63 × 2) = 282
Either stylist would cost $282 if the shoot lasted 2 hours.
To know more about Mathematical Expressions refer to the link:
https://brainly.com/question/1852123
#SPJ1
. sam flipped a coin 30 times and recorded 20 heads/10 tails. compare the theoretical and experimental probability.
Answers
Sam's experimental probability of getting heads in 30 coin flips was 20 out of 30, while the theoretical probability of getting heads is 1/2 or 0.5.
Sam's experimental probability of getting heads in the 30 coin flips was 20 out of 30, which can be written as 20/30 or simplified to 2/3. This means that in the experiment, heads appeared in approximately two-thirds of the flips. On the other hand, the theoretical probability of getting heads in a fair coin flip is 1/2 or 0.5. This is because there are two equally likely outcomes (heads or tails) and only one of them is heads.
Comparing the experimental and theoretical probabilities, we can see that Sam's results deviate slightly from the expected outcome. The experimental probability of getting heads is higher than the theoretical probability. This could be due to chance or random variation, as 30 coin flips may not be enough to perfectly represent the true probability. With a larger number of trials, the experimental probability would tend to converge towards the theoretical probability. However, in this specific experiment, Sam's results suggest a slightly biased coin favoring heads.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Whats the multiplier or divisor for each pair of equivalent fractions 5\6=10\12
Answers
Answer:
*12 and *6
Step-by-step explanation:
5*12/6*12=10*6/10*6
60/72=60/72
60=60
true
6th grade math HELPP ME!! Ya'll brainly has answers for this question but they're all different answers!! I'm so unsure! IF YOU DONT KNOW THE ANSWER PLEASE DO NOT ANSWER IMPROPERLY *I'm running out of points to ask the questions*
One of the offices at the company was being repainted. Riley’s mother challenged him to figure out how many quarts of paint would be needed. The office is 16 ft long and 12 ft wide, and the height of each wall is 10 ft. The office floor, ceiling, and door are not being painted, and there are no windows in this office. The door opening measures 3 ft by 8 ft. One quart of paint covers 2 100 ft . How many quarts of paint are needed to paint the room, if only full quarts can be purchased? Show your work.
Answers
Step-by-step explanation:
a lot measuring 120' x 200' is selling for $300 a front foot. what is its price?
Answers
The price of the lot measuring 120' x 200', selling for $300 a front foot is $192,000.
To find out the price of a lot measuring 120' x 200', selling for $300 a front foot, you need to use the formula given below;
Price = Front Footage × Price per Front Foot
First, you need to calculate the front footage of the lot, which can be obtained by adding up the length of all the sides of the rectangular lot.
Front footage = 120 + 120 + 200 + 200
= 640 ft
Then you can find the price of the lot by multiplying the front footage by the price per front foot.
Price = 640 ft × $300/ft
= $192000
Therefore, the price of the lot measuring 120' x 200', selling for $300 a front foot is $192,000.
Learn more about selling price:
https://brainly.com/question/29065536
#SPJ11
lolllll helppp me out sorry

Answers
Olivia was pocking up some of her old stuff into a box. A box can hold 8
pounds, but she only filled it up full How much weight was in the bon?
3/5
Answers
Answer:
Step-by-step explanation:
2 easy ways:
1. Divide 7 by 3 then multiply by 2
7/3= seven thirds or 2.333
Now multiply by two to get 14 thirds
or 4.666
2. Multiply 7 by 2/3, or 0.666
This way is a lot easier with a
calculator
The weight of the box is 14/3’s or 4.666
Write the equation of the line passing through(3,5) and (0,2).
Answers
Answer: y = 3x + 2
Step-by-step explanation:
Let's start with what we know. To calculate the slope, we do:
(y1 - y2)/(x1 - x2)
So, for this equation we get:
(5 - 2)/(3-0)
We get 3/3, so the slope = 1. So far, we have:
y = 3x + b
Let's use one of our coordinates to plug this in:
2 = 0 + b
So b = 2.
So our final equation is:
y = 3x + 2
Sort these numbers:

Answers
Answer:
multiples of 50: 50, 450, 500
not multiples: 515, 410, 555, 540
Step-by-step explanation:
Gabriel invests money in an account paying a simple interest of 3.7% per year. If he invests $110 and no money will be added or removed from the investment, how much will he have in one year, in dollars and cents?
Answers
\(~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \$110\\ r=rate\to 3.7\%\to \frac{3.7}{100}\dotfill &0.037\\ t=years\dotfill &1 \end{cases} \\\\\\ A=110[1+(0.037)(1)]\implies A=110(1.037)\implies A=104.07\)
Suppose that the market demand for landscaping services is given by the following equation:Qd = 479 - 3Pwhere Qd is the quantity of residential landscape cleanings per week that people in the local area would be willing to purchase at a monthly price of P dollars.What is the quantity demanded at a price of 39 dollars per month?
Answers
Answer:
Explanation:
Given:
Qd = 479 - 3P
where:
Qd = the quantity of residential landscape cleanings per week that people in the local area would be willing to purchase
P = monthly price in dollars
We plug in the given price of 39 dollars per month into Qd = 479 - 3P. So,
\(\begin{gathered} Qd=\text{ 479-3p} \\ =479-3(39) \\ \text{Simplify} \\ =479-117 \\ Qd=362 \end{gathered}\)Therefore, the quantity demanded at a price of 39 dollars per month is 362.
Graph the reflection of the polygon in the given line #11
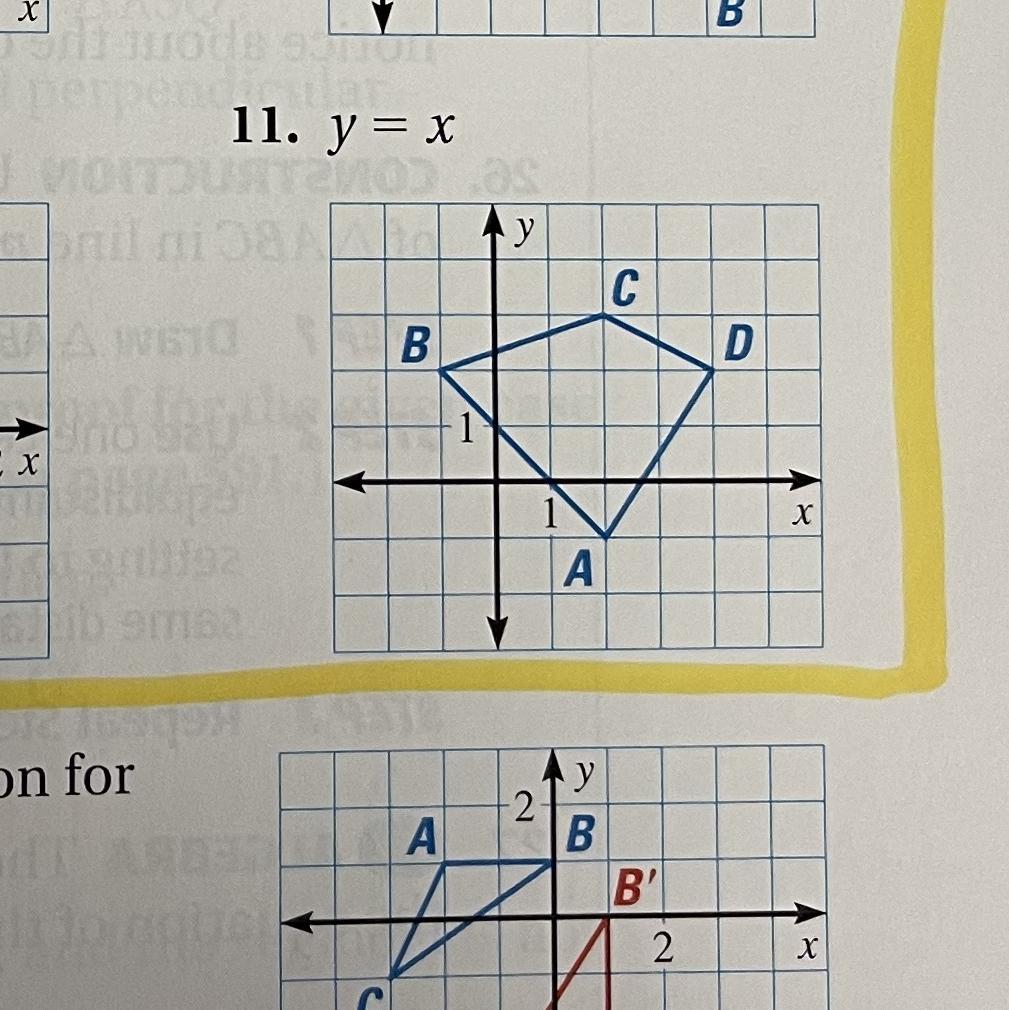
Answers
Let:
\(\begin{gathered} A=(2,-1) \\ B=(-1,2) \\ C=(2,3) \\ D=(4,2) \end{gathered}\)After a reflection across the line y = x:
\(\begin{gathered} A->(y,x)->A^{\prime}=(-1,2) \\ B->(y,x)->B^{\prime}=(2,-1) \\ C->(y,x)->C^{\prime}=(3,2) \\ D->(y,x)->D^{\prime}=(2,4) \end{gathered}\)
- 4j - 1 - 4j+6
Write that expression in the simplest form
Answers
Answer:
-8j+5
Step-by-step explanation:
the answer is -8j+5
HELP ASAPPPPP!! PLEASE :D

Answers
The domain of the quadratic function f(x) = x² - 10x + 22 include the following: D. all real numbers.
How to determine of this quadratic function?In Mathematics, the horizontal extent of any graph of a function represents all domain values and they are always read and written from smaller to larger numerical values, and from the left of the graph to the right.
Generally speaking, the domain of a quadratic function (parabola) is always all the real numbers that are located on the x-axis of a cartesian coordinate.
In conclusion, the domain of this quadratic function are all the x-values (independent value) that are located on the x-axis of the graph, which include {-∞, ∞} or all real numbers.
Read more on domain here: brainly.com/question/17812730
#SPJ1
PLEASE HELP! ASAP I WILL GIVE BRAINLIEST
This table represents the monthly fees for checking accounts at two banks.
Which statement is best supported by the information in the table?
The fee at Sunset Bank will always be less than the fee at Oceanview Bank.
The fee at Sunset Bank will be less than the fee at Oceanview Bank only when the checking account balance is less than $200.
The fee at Sunset Bank will be less than the fee at Oceanview Bank only when the checking account balance is more than $200.
The fee at Sunset Bank will always be more than fee at Oceanview Bank.

Answers
Answer:
the fee at sunset bank will always be more than fee at Oceanview bank.
Answer:
D
Step-by-step explanation:
i got it correct and go to k-12
The first four numbers of the pattern are 4., 3.6, 3.2, and 2.8 . Find the next three numbers in the pattern
Answers
Answer:
Step-by-step explanation:
4 - 0.4 = 3.6
3.6 - 0.4 = 3.2
2.8 - 0.4 = 2.4
2.4 - 0.4 = 2
2 - 0.4 = 1.6
so the next numbers in the pattern are: 2.4, 2 and 1.6
What is the first quartile of the data shown in the box plot

Answers
Answer:
55 to 70
Step-by-step explanation:
The first quartile is the left-most region of the graph, from 55 to 70. The second quartile stretches from 70 to 80.