Claire has quarters and nickels in her purse. The total value of the coins is $2.65. Which equation can be used to find x, the number of quarters in Claire’s purse?
Coins in Claire’s Purse
Coin
Number of coins
Nickels
2x + 4
Quarters
x
5 (2 x + 4) + 25 x = 2.65
0.05 (2 x + 4) + 0.25 x = 2.65
0.5 (2 x + 4) + 0.25 x = 2.65
(2 x + 4) + x = 2.65
Answers
Answer:
0.05(2x +4) +0.25x =2.65
Step-by-step explanation:
The decimals are in the right places. A. would have been correct but it would have had to be 265 instead of 2.65. They put the decimals in the incorrect place.
Answer:
0.05(2x +4) +0.25x =2.65 or b
Step-by-step explanation:
edge 2021
Related Questions
Use the number line to find the missing value. +(-4)=-1

Answers
The value of the missing number will be 3.
What is a number line?A number line in elementary mathematics is a representation of a graduated straight line that serves as an abstraction for real numbers, represented by the symbol R."
It is assumed that every point on a number line corresponds to a real number and that every real number corresponds to a point.
The equation for the missing number is given as x + (-4) = -1. the missing number will be calculated as:-
x + (-4) = -1
x -4 = -1
x = 4 - 1
x = 3
To know more about number lines follow
https://brainly.com/question/24644930
#SPJ1

¿Qué línea parece tener una intersección con el eje x de-5 y una intersección con el eje y de 37?
Answers
Answer: -5x + 37
Step-by-step explanation:
PLEASE HURRY AND ANSWER!!!!

Answers
The probability that that arrow will land on the part labelled C after the first spin would be = 1/5.
How to calculate the probability of the chosen event?To calculate the probability of the chosen event, the formula for probability should be used which is given as follows:
Probability = possible outcome/ sample space
Where possible outcome = 2
sample space = A,B,B,B,C,C,D,D,D,E = 10
Therefore the probability that the arrow will land on the part labelled C after the first spin = 2/10 = 1/5.
Learn more about probability here:
https://brainly.com/question/30657432
#SPJ1
Of the 32 students in Joe's class, 8 students ride their bikes to school, 5 walk to school, 4 get a ride to school in a car, and 15 take the bus to school. What is the experimental probability of choosing a student who walks to school?
Answers
The experimental probability of choosing a student who walks to school is given by 0.15625 or 15.625%.
Given data ,
The experimental probability of choosing a student who walks to school can be calculated by dividing the number of students who walk to school by the total number of students in Joe's class.
Number of students who walk to school = 5
Total number of students in the class = 32
Experimental probability = Number of students who walk to school / Total number of students
= 5 / 32
P = 0.15625
Hence , the experimental probability of choosing a student who walks is 0.15625 or 15.625%.
To learn more about probability click :
https://brainly.com/question/17089724
#SPJ1
Benny spent $55 buying lunch for his office. If there are 20 people in the office, how much did each lunch cost? PLEASE HELP ME FAST ILL LOVE U FOREVER I SWEAR. <3
Answers
Answer:
$2. 75
Step-by-step explanation:
If he spent $55 on 20 lunches then each lunch was $2. 75
2. 75×20= 55
Answer:
Hey! so the answer is $2.75
Step-by-step explanation:
If he spet 55 dollars for the office you would have to divide the money to the number of people. so therefore $2.75.
Also, you dot have to love me ^-^.
Hoped this helped Im Eve btw. Hope you have a great day and consider marking this brainliest Thank you so much if you do! ✨
lect the correct answer.
Under which condition is the sample proportion, , a point estimate of the population proportion?
A.
The sample proportion is never a point estimate of the population proportion.
B.
The sample represents a proportion of the population.
C.
The sample proportion is unbiased.
D.
The sample size, n, is small enough.
Reset Next
Answers
The correct answer is B. The sample represents a proportion of the population.
What is the sample population ?
A point estimate is a single value used to estimate a population's unknown parameter. The sample proportion (denoted by p), in the context of determining the population proportion, is a widely used point estimate. The sample proportion is determined by dividing the sample's success rate by the sample size.
The sample must be representative of the population for it to be a reliable point estimate of the population proportion. To accurately reflect the proportions of various groups or categories present in the population, the sample should be chosen at random.
Learn more about population:https://brainly.com/question/30324262
#SPJ1
Glen invited 25 people to his birthday party.
20 people attended the party and 5 people did not attend.
What percent of the people whom Glen invited did not attend the party?
Answers
Answer:
20% of the invited people did not attend
Step-by-step explanation:
5 out of 25 people invited didn't attend Glen's party. That means the following:
\(\frac{5}{25}\) people didn't come which simplifies to \(\frac{1}{5}\)
Multiply \(\frac{1}{5}\) by the giant one \(\frac{20}{20}\) so the denominator is 100 which is the denominator used to find percentages.
You end up with \(\frac{20}{100}\)
\(\frac{20}{100}\) = 20%
20% is the percentage of the people whom Glen invited did not attend the party.
To find the percentage of people who did not attend the party, we will divide the number of people who did not attend (5) by the total number of people invited (25), and then multiply by 100.
Percentage = (Number of people not attended / Total number of people invited) × 100
Percentage = (5 / 25) × 100
Percentage = 20%
So, 20% of the people whom Glen invited did not attend the party.
Learn more about percentage here:
https://brainly.com/question/24877689
#SPJ3
pls help me with this

Answers
The expression of the perimeter of the triangle is 15h - 6k + 12m.
How to find the perimeter of a triangle?A triangle is a polygon with three sides. The sum of angles in a triangle is 180 degrees.
The perimeter of a triangle is the sum of the whole three sides of the triangle.
Therefore, let's find the perimeter of the triangle with side length (5h - 4k), (10h + 7m) and (5m - 2k).
Therefore,
perimeter of a triangle = 5h - 4k + 10h + 7m + 5m - 2k
collect like terms
perimeter of a triangle = 5h + 10h - 4k - 2k + 7m + 5m
Therefore,
perimeter of a triangle = 15h - 6k + 12m
learn more on perimeter here: https://brainly.com/question/29507476
#SPJ1
My question is
4(2 - W) + w = 20
Answers
Answer:
- 4
Step-by-step explanation:
Step 1:
4 ( 2 - w ) + w = 20 Equation
Step 2:
8 - 4w + w = 20 Multiply
Step 3:
8 - 3w = 20 Combine Like Terms
Step 4:
- 3w = 12 Subtract 8 on both sides
Answer:
w = - 4
Hope This Helps :)
Answer:
w = -4
Step-by-step explanation:
4(2 - W) + w = 20
Distribute:
8 - 4w + w = 20
Subtract 8 from both sides:
-4w + w = 12
Simplify:
-3w = 12
Divide:
w = -4
Double check your work by substitution:
4(2 - W) + w = 20
4(2 - (-4)) + (-4) = 20
4(6) + (-4) = 20
24 + (-4)= 20
20 = 20
Since we know that 20 does equal 20, we can conclude that the final answer is:
w = -4
Solve using substitution.
y = –6
–8x − 7y = –6
Answers
Okay so you put -6 in where y is then solve and youll get your answer
-8x-7(-6)=-6
If there are 9 tacos, 18 hot dogs, and 6 hamburgers, which foods have a ratio of 2:3?
Answers
Answer:
Hamburgers and Tacos.
Step-by-step explanation:
If you divide 6 by 3 you get 2, and if you divide 9 by 3 you get 3.
2:3
Solve the equation.
5.16 = 4n
Show your work.
Answers
Answer:
5.16=4n
Step 1: Flip the equation.
4n=5.16
Step 2: Divide both sides by 4.
4n/4= 5.16/4
anwers n=1.29
Step-by-step explanation:
I hope this help ;-)
a floor that is 15 15 feet by 12 feet is being covered by tiles that are 1.5 feet by 1.5 feet. which is the best represents the number of tiles that will be needed
Answers
The best representation of the number of tiles that will be needed to cover the Floor is 80 tiles.
The number of tiles needed to cover the floor, we can calculate the total area of the floor and divide it by the area of each tile.
The area of the floor is given by the product of its length and width: 15 feet * 12 feet = 180 square feet.
The area of each tile is given by the product of its length and width: 1.5 feet * 1.5 feet = 2.25 square feet.
To find the number of tiles needed, we divide the total area of the floor by the area of each tile:
Number of tiles = (Total area of the floor) / (Area of each tile) = 180 square feet / 2.25 square feet = 80 tiles.
therefore, the best representation of the number of tiles that will be needed to cover the floor is 80 tiles.
To know more about Floor .
https://brainly.com/question/30625339
#SPJ8
Find the equation for the tangent to the curve of f at the point:f(x) = (3x+1)² , x = -1
Answers
The eqaution of the tangent at the point x = -1 is:
\(y=-12x-8\)To solve this, first, we need to find the value of y when x = -1:
\(f(-1)=(3\cdot(-1)+1)^2=(-3+1)^2=(-2)^2=4\)Then we want to find the equation of the tangent at the point (-1, 4)
The next step is to find the derivative of the equation, because the derivative thell us the slope of the tangent line at a certain point:
\(\begin{gathered} f(x)=(3x+1)^2 \\ f^{\prime}(x)=2(3x+1)\cdot3=6(3x+1)=18x+6 \\ \\ f^{\prime}(x)=18x+6 \end{gathered}\)Now that we have the derivative, let's calculate the slope of the tangent like in the point (-1, 4). To do this, we evaluate the derivative in x = -1:
\(f^{\prime}(-1)=18\cdot(-1)+6=-18+6=-12\)The slope of the tangent line is -12.
Now we have all the necessary things to construct the equation of a line: we have the slope (-12) and a point (-1, 4).
The slope-point form of a line is:
\(\begin{gathered} y=m(x-x_0)+y_0 \\ \end{gathered}\)Where m is the slope and x0, y0 are the x and y coordinates of a point
Then:
\(\begin{gathered} \begin{cases}m=-12 \\ x_0=-1 \\ y_0=4\end{cases} \\ y=-12(x-(-1))+4=-12\mleft(x+1\mright)+4=-12x-12+4=-12x-8 \end{gathered}\)And that's the equation of the line y = -12x - 8
In a survey of 259 professional athletes, it was found that 110 of them owned a convertible, 91 of
them owned a giant screen TV, and 120 owned a sporting goods store. 15 owned a convertible and a
store, 43 owned a TV and a store, and 44 owned a covertible and a TV. 9 owned all three items.
1. How many athletes did not own any of the three items?
2. How many owned a covertible and a TV, but not a store?
3. How many athletes owned a convertible or a TV?
4. How many athletes owned exactly one type of item in the survey?
5. How many athletes owned at least one type of item in the survey?
6. How many owned a TV or a store, but not a convertible?
Answers
1. Number of athletes did not own any of the three items = 259 - 228
= 31.
2. Number of athletes own a convertible and a TV but not a store = 44 - 9
= 35.
3. Number of athletes own a convertible or a TV = 110 + 91 - 44
= 157.
4. Number of athletes owned exactly one type of item = 60 + 13 + 71 = 144.
5. Number of athletes owned at least one type of item = 259 - 31
= 228
6. Number of athletes own a TV or a store, but not a convertible = 13 + 34 +71
= 118.
The number of athletes did not own any of the three items need to subtract the number of athletes who own at least one item from the total number of athletes surveyed.
Total number of athletes surveyed = 259
Number of athletes own at least one item = 110 + 91 + 120 - 15 - 43 - 44 + 9 = 228
Number of athletes who did not own any of the three items = 259 - 228 = 31.
The number of athletes who owned a convertible and a TV but not a store need to subtract the number of athletes who own all three items from the number of athletes who own a convertible and a TV.
Number of athletes who own a convertible and a TV = 44
Number of athletes who own all three items = 9
Number of athletes who own a convertible and a TV but not a store = 44 - 9 = 35
The number of athletes who owned a convertible, or a TV need to add the number of athletes who own a convertible to the number of athletes who own a TV and then subtract the number of athletes own both a convertible and a TV.
Number of athletes who own a convertible or a TV = 110 + 91 - 44
= 157.
The number of athletes owned exactly one type of item need to add up the number of athletes who own a convertible only the number of athletes own a TV only and the number of athletes who own a store only.
Number of athletes own a convertible only = 110 - 15 - 9 = 86
Number of athletes own a TV only = 91 - 44 - 9 = 38
Number of athletes own a store only = 120 - 15 - 43 - 9 = 53
Number of athletes owned exactly one type of item = 60 + 13 + 71 = 144.
The number of athletes who owned at least one type of item can use the result from part (1).
Number of athletes who owned at least one type of item = 259 - 31
= 228
The number of athletes who owned a TV or a store but not a convertible need to subtract the number of athletes who own all three items, and the number of athletes own a convertible and a TV from the number of athletes own a TV or a store.
Number of athletes own a TV or a store = 91 + 120 - 43 - 9 = 159
Number of athletes own a TV or a store not a convertible = 13 + 34 +71
= 118.
For similar questions on athletes
https://brainly.com/question/25631156
#SPJ11
Let f(x) = x ^ 2 + 5 and g(x) = sqrt(x - 5) Find the rules for (fg)(x) (gf)(x)
Answers
Answer:
To find the rules for (fg)(x) and (gf)(x), we need to evaluate the composite functions.
(fg)(x) = f(g(x)) = f(sqrt(x - 5)) = (sqrt(x - 5))^2 + 5 = x - 5 + 5 = x
(gf)(x) = g(f(x)) = g(x^2 + 5) = sqrt(x^2 + 5 - 5) = sqrt(x^2) = |x|
Therefore, the rules for (fg)(x) and (gf)(x) are:
(fg)(x) = x
(gf)(x) = |x|
Step-by-step explanation:
particle travels from(-1/3 ,1, -2) to(9,9,6) . Its motion is described by the position function r(t)=(t^3/3, t^2,2t).
a) Find the distance the particle travels along the path, its average speed, and its
displacement [the distance it could have traveled if in a straight line].
b) List a detailed snapshot of the T,N,B frame for this particle at the halfway point (by
time) including curvature and torsion.
Answers
The particle travels approximately 45.63 units along the path. The displacement is the straight-line distance between the initial and final positions of the particle is 2781.
To find the distance the particle travels along the path, we can integrate the speed over the interval of time. The speed of the particle is given by the magnitude of its velocity vector.
The velocity vector is the derivative of the position function r(t):
\(v(t) = (d/dt)(t^3/3, t^2, 2t)\)
\(= (t^2, 2t, 2)\)
The speed of the particle at any given time t is:
|v(t)| = √((t^2)^2 + (2t)^2 + 2^2)
= √(t^4 + 4t^2 + 4)
= √((t^2 + 2)^2)
To find the distance traveled along the path, we integrate the speed function over the given interval of time. The particle travels from t = -1/3 to t = 9.
distance = ∫[from -1/3 to 9] |v(t)| dt
= ∫[from -1/3 to 9] |t^2 + 2| dt
= ∫[from -1/3 to 0] -(t^2 + 2) dt + ∫[from 0 to 9] (t^2 + 2) dt
= [-1/3 * t^3 - 2t] (from -1/3 to 0) + [1/3 * t^3 + 2t] (from 0 to 9)
Evaluating the definite integrals:
distance = [-1/3 * 0^3 - 2 * 0 - (-1/3 * (-1/3)^3 - 2 * (-1/3))] + [1/3 * 9^3 + 2 * 9 - (1/3 * 0^3 + 2 * 0)]
= [0 - (1/3 * (-1/27) + 2/3)] + [1/3 * 729 + 18]
= [1/27 + 2/3] + [729/3 + 18]
= 1/27 + 2/3 + 729/3 + 18
= 1/27 + 18/27 + 729/3 + 18
= (1 + 18 + 729)/27 + 18
= 748/27 + 18
= 27.63 + 18
= 45.63 units (approximately)
Therefore, the particle travels approximately 45.63 units along the path.
To find the average speed, we divide the distance traveled by the time taken. The time taken is 9 - (-1/3) = 9 1/3 = 28/3.
average speed = distance / time
= 45.63 / (28/3)
= 45.63 * (3/28)
= 4.9179 units per unit time (approximately)
The displacement is the straight-line distance between the initial and final positions of the particle.
displacement = |r(9) - r(-1/3)|
= |(9^3/3, 9^2, 2 * 9) - ((-1/3)^3/3, (-1/3)^2, 2 * (-1/3))|
= |(27, 81, 18) - (-1/27, 1/9, -2/3)|
= |(27 + 1/27, 81
= 2781.
For more such questions on displacement , Visit:
https://brainly.com/question/1581502
#SPJ11
Georgia brought a snow cone shaped like the cone below what is the height of the snow cone

Answers
Answer:
Step-by-step explanation:
Use the Pythagorean Theorem.
h² = 5² - 3² = 4²
h = 4 in
Please help !?:(
Use the distributive property and modeling to perform the
following function operations.
Let f(x) = 3x^2 + 4x + 2 and g(x) = 2x +3.
Find f(x) g(x).

Answers
dont no sory need some points plz answer my question
NO LINKS!!! URGENT HELP PLEASE!!!
Solve ΔABC using the Law of Sines
1. A = 29°, C = 63°, c = 24
2. A = 72°, B= 35°, c = 21
Answers
Answer:
1) B = 88°, a = 13.1, b = 26.9
2) C = 73°, a = 20.9, b = 12.6
Step-by-step explanation:
To solve for the remaining sides and angles of the triangle, given two sides and an adjacent angle, use the Law of Sines formula:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Question 1Given values:
A = 29°C = 63°c = 24As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies B=180^{\circ}-A-C\)
\(\implies B=180^{\circ}-29^{\circ}-63^{\circ}\)
\(\implies B=88^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies a=\dfrac{24\sin 29^{\circ}}{\sin 63^{\circ}}\)
\(\implies a=13.0876493...\)
\(\implies a=13.1\)
Solve for b:
\(\implies \dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies b=\dfrac{24\sin 88^{\circ}}{\sin 63^{\circ}}\)
\(\implies b=26.9194211...\)
\(\implies b=26.9\)
\(\hrulefill\)
Question 2Given values:
A = 72°B = 35°c = 21As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies C=180^{\circ}-A-B\)
\(\implies C=180^{\circ}-72^{\circ}-35^{\circ}\)
\(\implies C=73^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies a=\dfrac{21\sin 72^{\circ}}{\sin 73^{\circ}}\)
\(\implies a=20.8847511...\)
\(\implies a=20.9\)
Solve for b:
\(\implies \dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies b=\dfrac{21\sin 35^{\circ}}{\sin 73^{\circ}}\)
\(\implies b=12.5954671...\)
\(\implies b=12.6\)
The distribution of the amount of money spent by students on textbooks in a semester is approximately normal in shape with a mean of 349 and a standard deviation of 24. According to the standard deviation rule, approximately 95% of the students spent between _____$ and _____$ on textbooks in a semester.
Question 12
Type numbers in the boxes.
1 points
The distribution of IQ (Intelligence Quotient) is approximately normal in shape with a mean of 100 and a standard deviation of 16. According to the standard deviation rule, ______% of people have an IQ between 52 and 148. Do not round.
Question 13
Type numbers in the boxes.
10 points
The distribution of IQ (Intelligence Quotient) is approximately normal in shape with a mean of 100 and a standard deviation of 13. According to the standard deviation rule, only _____% of people have an IQ over 139.
Question 14
Type numbers in the boxes.
10 points
The distribution of the amount of money spent by students on textbooks in a semester is approximately normal in shape with a mean of: μ= 310 and a standard deviation of: σ= 36.
According to the standard deviation rule, almost 2.5% of the students spent more than what amount of money on textbooks in a semester? _____
Answers
(b) is the correct response. the students spend on textbooks in a semester between $250 and $2,000
The Gaussian distribution is another name for the normal distribution. It is a typical continuous probability distribution with a standard deviation of one and a mean of zero.
The tails of the curve are asymptotic, extending to infinity without touching the horizontal axis, and the curve is unimodal and symmetric about the mean. Since the majority of observations are centered on the mean, mean=mode=median.
99.7% of the area under the curve is approximately -3, or 3 standard deviations from the mean, according to the 68-95-99.7 rule. The z score is determined utilizing the accompanying recipe:
For z=3, solve for both x by equating the z score formula with -3 and 3.
3 = x 235 5 x = (3 5) + 235 x = 250 for z=-3:
3 = x 235 5 x = (3 5) + 235 x = 220 A student spends between $220 and $250 on textbooks each semester.
To learn more about normal distribution here
https://brainly.com/question/29509087
#SPJ4
Full Question = The distribution of the amount of money spent by students for textbooks in a semester is approximately normal in shape with a mean of $235 and a standard deviation of $5. According to the standard deviation rule, how much did almost all (99.7%) of the students spend on textbooks in a semester?
a. Between 230 and 240 dollars.
b. Between 220 and 250 dollars.
c. Between 175 and 295 dollars.
d. Less than 220 dollars or more than 250 dollars.
e. Less than 230 dollars or more than 240 dollars.
Find the value of y.

Answers
The value of y is 4√3
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths. The corresponding angles of similar triangles are congruent or equal.
Also , the ratio of corresponding sides of similar triangles are equal.
There are two triangles that are similar
Therefore;
y /16 = 4/y
y² = 48
y = √48
y = √16 × √ 3
y = 4√3
Therefore, the value of y is 4√3
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
how are the probability of an event and the probability of its complement related mathematically
Answers
The relation between the probability of its complement is that their sum is 1.
Complement in probability theory is an essential concept that helps us understand the likelihood of an event not occurring. It is a mathematical term that refers to the opposite or negation of an event.
Complement refers to the probability of an event not occurring, given the probability of it occurring. It is often denoted as the complement of an event A and is represented by A’.
The complement of an event A is defined as the set of all outcomes in the sample space that are not in A.
The probability of the complement of A is equal to the probability of all the outcomes in the sample space that are not in A.
The most important properties of the complement of an event is that the probability of an event and its complement always add up to 1. This is known as the law of complementary probability, and is expressed as:
P(A) + P(A’) = 1
This means that if we know the probability of an event occurring, we can easily calculate the probability of its complement by subtracting the probability of the event from 1.
For example, if the probability of event A is 0.7, then the probability of its complement, A’, is 1 – 0.7 = 0.3.
Hence the relation between the probability of its complement is that their sum is 1.
Learn more about probability click;
https://brainly.com/question/17256887
#SPJ1
In what quadrant are the eyeglasses

Answers
Answer:
3rd Quadrant
Step-by-step explanation:
Hope the above solution will help you
please help 10 points for the question i dont know why but my brain cannot compute this question

Answers
9514 1404 393
Answer:
(b) 6^10/7^6
Step-by-step explanation:
The applicable rules of exponents are ...
(a/b)^c = (a^c)/(b^c)
(a^b)^c = a^(bc)
__
This means you have ...
\(\left(\dfrac{6^5}{7^3}\right)^2=\dfrac{(6^5)^2}{(7^3)^2}=\dfrac{6^{5\cdot2}}{7^{3\cdot2}}=\boxed{\dfrac{6^{10}}{7^6}}\)
__
Additional comment
I find it helpful to remember that an exponent signifies repeated multiplication. Then ...
\(\left(\dfrac{6^5}{7^3}\right)^2=\left(\dfrac{6^5}{7^3}\right)\cdot\left(\dfrac{6^5}{7^3}\right)=\dfrac{6^5\cdot6^5}{7^3\cdot7^3}=\dfrac{6^{5+5}}{7^{3+3}}=\dfrac{6^{10}}{7^6}\)
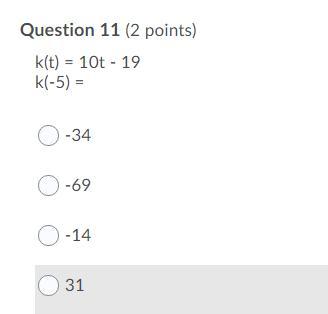
k(t) = 10t - 19
k(-5) =
Answers
Answer:
-69
Step-by-step explanation:
k(-5) = 10*-5 -19
= -50-19
=-69
-69
Hope this helps
Can someone please help, ty!!
(Will mark brainliest)

Answers
Answer:
6th graders
Step-by-step explanation:
The median is actually just the line inside the box of the box-and-whisker plot.
Notice that for 6th graders, the median is at about 2.4, while for 4th graders, the median is at about 1.5.
Clearly, the 6th graders have the higher median.
what is 23^a x 23^b= Pls I need the answer
Answers
Answer:
23^(a+b)
Step-by-step explanation:
23^a x 23^b =23^(a+b)
The lengths of the sides of triangle XYZ are written in terms of the variable m, where m ≥ 6.
Triangle X Y Z is shown. The length of side X Y is m + 8, the length of side Y Z is 2 m + 3, the length of side Z X is m minus 3.
Which is correct regarding the angles of the triangle?
mAngleX < mAngleZ < mAngleY
mAngleY < mAngleZ < mAngleX
mAngleY < mAngleX < mAngleZ
mAngleZ < mAngleY < mAngleX
Answers
The correct arrangement regarding the angles of the triangle is;
m∠Y < m∠Z < m∠X
What are the missing angles of the triangle?In triangle XYZ, the lengths of sides are;
XY = m + 8
YZ = 2m + 3
ZX = m - 3
If m ≥ 6, then;
m + 8 ≥ 14
2m + 3 ≥ 15
m - 3 ≥ 3
Thus;
m - 3 ≤ m + 8 ≤ 2m + 3
The greatest angle is opposite to the greatest side, the smallest angle is opposite to the smallest side, so;
the greatest side is YZ = 2m + 3- the greatest angle is ∠X
the smallest side is ZX = m - 3 - the smallest angle is ∠Y
Read more about angles in a triangle at; https://brainly.com/question/25215131
#SPJ1
The scatterplot contains data points, pairing the age of a child (x) with the child’s weight (y). Using the least-squares regression method, which is the line of best fit?

Answers
Using the least-squares regression method, the line of best fit is line d.
Why is line d the line of best fit?According to the graph, we can see that the sum of distance to line d is smallest ( least-square).
Least-squares regression is a statistical technique employed to ascertain the optimal line of best fit within a dataset. This line is determined by minimizing the total sum of squared discrepancies between the observed y-values and the predicted y-values that lie on the line.
In this method, we aim to find the line that best captures the relationship between the variables by minimizing the squared differences. By doing so, we strive to minimize the overall error and maximize the accuracy of the line in representing the data.
Learn about least-square regression here https://brainly.com/question/14563186
#SPJ1