[(2/3)^2]^3 X (2/3)^2 ÷ (2/3)^8
Answers
Answer:
Reduce the expression, if possible, by cancelling the common factors.[(2/3)^2]^3 X (2/3)^2 ÷ (2/3)^8 = 1
Step-by-step explanation:
4/9^3 x (2/3)^2 ÷ (2/3)^8
4/9^3 x 4/9 ÷ (2/3)^8
4/9^3 x 4/9 divided by 256/6561
64/729 x 4/9 divided by 256/6561
= 1
Related Questions
A car salesperson had $85,460 in total monthly sales in September and $74,570 in October. The salesperson earned a total of $3,485 in commission from those sales combined.
What is the salesperson's commission as a percent of the total monthly sales?
Enter your answer, rounded to the nearest tenth of a percent, in the box.
Answers
Answer:
2.2%
Step-by-step explanation:
i took the test!
Find the product using the FOIL method.
(q-2)(q-8)
Answers
=q^2-10q+16
Answer:
q²-10q+16
Step-by-step explanation:
FOIL stands for:
First -> (q-2)(q-8)
Outer -> (q-2)(q-8)
Inner -> (q-2)(q-8)
Last -> (q-2)(x-8)
Following FOIL, we get:
(q-2)(q-8)
(q)(q)+(q)(-8)+(-2)(q)+(-2)(-8)
q²-8q-2q+16
q²-10q+16
Therefore, the expanded form is q²-10q+16
Are these shapes congruent or similar?

Answers
Answer:
congruent
Step-by-step explanation:
Zaboca Printing Limited (ZPL) has only one working printer. Eight (8) customers submitted their orders today Monday 6th June 2022. The schedule of delivery of these orders are as follows:
Jobs (in order of arrival) Processing Time (Days) Date Due
A 4 Monday 13th June 2022
B 10 Monday 20th June 2022
C 7 Friday 17th June 2022
D 2 Friday 10th June 2022
E 5 Wednesday 15th June 2022
F 3 Tuesday 14th June 2022
G 8 Thursday 16th June 2022
H 9 Saturday 18th June 2022
All jobs require the use of the only printer available; You must decide on the processing sequence for the eight (8) orders. The evaluation criterion is minimum flow time.
i. FCFS
ii. SOT
iii. EDD
iv. CR
v. From the list (i to iv above) recommend the best rule to sequence the jobs
Answers
The recommended rule to sequence the jobs for minimum flow time is the EDD (Earliest Due Date) rule.
The EDD rule prioritizes jobs based on their due dates, where jobs with earlier due dates are given higher priority. By sequencing the jobs in order of their due dates, the goal is to minimize the total flow time, which is the sum of the time it takes to complete each job.
In this case, applying the EDD rule, the sequence of jobs would be as follows:
D (Due on Friday 10th June)
F (Due on Tuesday 14th June)
E (Due on Wednesday 15th June)
C (Due on Friday 17th June)
G (Due on Thursday 16th June)
H (Due on Saturday 18th June)
A (Due on Monday 13th June)
B (Due on Monday 20th June)
By following the EDD rule, we aim to complete the jobs with earlier due dates first, minimizing the flow time and ensuring timely delivery of the orders.
Therefore, the recommended rule for sequencing the jobs in this scenario is the EDD (Earliest Due Date) rule.
Learn more about EDD here: brainly.com/question/30397523
#SPJ11
If x−y=9 is a true equation, what would be the value of 5+x−y?
Help please
Answers
Answer:
14
Step-by-step explanation:
5+x-y (x-y=9) so -----> 5+9=14
Answer:
5+9 = 14
Step-by-step explanation:
x-y = 9, so 5+x-y would be equal to 5+9
5+9 is 14
hope this helps!
if you have $11 and save $5 each week how much money you will have after 6 weeks
Answers
Answer: 41$
Step-by-step explanation:
This is because 5x6=30 (To find how much money is made)
then 11+30=41 (add both amounts)
What is -1 3 10 + (-3.8)?
Answers
Answer:
1
Step-by-step explanation:
1
What are the x and y -intercepts for the equation 5x - 4y = 10
Answers
Answer:
x=2
y= -2.5
Step-by-step explanation:
x int
1.) set y to 0 (5x -4(0)=10
solve for 5x=10
y int
1.) set x to 0
solve for -4y=10
Answer:
x=2, y=-5/2
Step-by-step explanation:
to find the 'x' intercept, set the 'y' value to zero and solve:
5x - 4(0) = 10
5x = 10
x = 2
to find the 'y' intercept, set the 'x' value to zero and solve:
x(0) - 4y = 10
-4y = 10
y = -10/4 or -5/2
Differentiation
Please help me!

Answers
Answer:
\( \frac{dy}{dx} = - 1 \frac{5}{9} \)
Step-by-step explanation:
Please see the attached picture for the full solution.
☆ \(\frac{1}{x} = x^{ - 1} \)

Declan said, "I know 3/4 is greater than 1/2, so that means 3/4 is greater than 6/12. " Does Declan’s reasoning make sense?
Answers
Declan's reasoning does make sense. This is because 3/4 and 1/2 have the same denominator, and 3/4 is a larger fraction than 1/2.
Therefore, it is reasonable to assume that 3/4 is greater than 6/12 because 6/12 simplifies to 1/2. Simplifying fractions means dividing the numerator and denominator by the same number, in this case, 6 is divisible by 2, so we can reduce the fraction to 1/2.
So, Declan is correct in his reasoning that 3/4 is greater than 6/12. It is important to understand the relationship between fractions and their denominators to make such comparisons accurately.
3/4 = 9/12
1/2 = 6/12
6/12 = 6/12
Since 9/12 (which is equivalent to 3/4) is greater than 6/12 (which is equivalent to 1/2), we can say that 3/4 is indeed greater than 6/12.
Therefore, Declan's reasoning is correct.
Learn more about Fractions:
https://brainly.com/question/78672
#SPJ4
what is the answer for this-order of operation?

Answers
Answer:
Step-by-step explanation:
always follow BODMAS or BIDMAS-
Do the multiplication, which is 15/3 and when simplifiyed becomes 5.
Then work out 6 divided by 3/2. In division for fractions, you always find the reciprocal of the 2nd number and multiply instead of divide, so its 6 x 2/3 which is 12/3, simplifiyed to be 4. 5+4=9. 9+10 is 19, and 19-4=15
600 ÷ 300 hey answers
Answers
Answer:
2
Step-by-step explanation:
I hope this helps you :)
Answer:
2
Step-by-step explanation:
Anything divided by 2 is half of itself. So 600 ÷ 300 would technically be 300. But in division we count the amount of times a number can go into the other number. So 600 divided by 300 is 2.
Kori spent 46.20 on 12 gallons of gas what was the price per gallon

Answers
Answer:
B.
Step-by-step explanation:
I did 46.20 divided by 12 and I got my answer.
Answer:
$3.85 per gallon
Step-by-step explanation:
46.20/12 = 3.85
A bag of sweets contains only gobstoppers and sherbert lemons.
There are 3 gobstoppers for every 4 sherbert lemons.
There are 56 sweets in the bag. How many gobstoppers are there?
Answers
gob + lem -> 3+4 = 7 (sweets in a "group")
56/7 = 8 (we have 8 "groups")
gobstoppers = their num in 1 "group" • num of "groups", so 3 • 8 = 24
Answer: 24 gobstoppers
Find the next term in each sequence.
Question 1:
0, 1, 3, 7, ? .
Question 2:
35, 33, 29, 21, ?.
Please Include an Explanation of how to solve problems like this!
Thanks a ton!
Answers
Question 2 is 5. It is the same as the first one but backwards. You would take the amount subtracted last time, multiply it by 2, and then subtract it from the number. Since 8 was subtracted last, 16 was subtracted this time.
The lifetimes of light bulbs are normally distributed with a mean of 500 hours and a standard deviation of 25 hours. Find the probability that a randomly selected light bulb has a lifetime that is greater than 532 hours
Answers
The probability that a randomly selected light bulb has a lifetime that is greater than 532 hours is 0.10027
How to determine the probability of the selected light bulbFrom the question, we have the following parameters that can be used in our computation:
Normal distribution, where, we have
Mean = 500
Standard deviation = 25
So, the z-score is
z = (x - mean)/SD
This gives
z = (532 - 500)/25
z = 1.28
So, the probability is
P = P(z > 1.28)
Using the table of z scores, we have
P = 0.10027
Hence, the probability is 0.10027
Read more about probability at
brainly.com/question/31649379
#SPJ4
= Problem 2. [Diffusion equation Green's function.] Consider the diffusion differential equation (given here in one dimension): au au B at = f(t). This equation describes the diffusion of particles in liquid or gas solution. Green's function for this equation is ƏG(, 19;t) 2G(, 2o:t) = 8(t)(x - 2) ar2 at (a) Using the same methods we used before find the Green's function for the one- dimensional problem with no boundaries. Recall the method: take Fourier trans- form of the equation, solve the resulting algebraic equation for FT Green's func- tion and FT back to the real space. Your result should be 1 ATT BE G(a 20,1) exp 487 Recall that in the equations of this type Green's function is probability of finding a particle at time t at position x which was at t = 0 at position to (b) Now suppose there is an absorbing wall at x = 0, and you are interested in the diffusion of particles in the region x > 0. Absorbing wall means that that prob- ability of finding a particle at x = 0 must be zero (once it reaches the boundary, the particle is immediately absorbed). You can solve this problem by method of images, using the result of part (a). The idea, same as in electromagnetism, is that by placing an 'image source' somewhere in the region x < 0 (which is not of interest in this problem), with the appropriate pre-factor, you can recreate appropriate boundary conditions at x = 0. Since this boundary condition is of Dirichlet type it guarantees the uniqueness of the solution - therefore the function you have found is the only solution. (c) Using Ficks's law j = -Bag/ox find the rate of absorption at the wall (r = 0). (d) (optional) If the wall at x = O were reflecting, the flux of particles through the wall is zero, but G(x=0) is not necessarily zero. Clearly, this is the boundary condition of the Neumann type, and the solution is unique. Find Green's function using the method of images in this case. Find the position of maximum probability density as a function of time.
Answers
The required Green's functions are:
a) ƏG(x, t; 20,t) = 1/(2√πBt) exp[-(x-20)²/4Bt].
b) ƏG(x, t; 20,t) = 1/(2√πBt) [exp[-(x-20)²/4Bt] - exp[-(x+20)²/4Bt]].
c) r = (5/2)B(20²/πt)exp(-100Bt).
d) ƏG(x, t; 20,t) = 1/(2√πBt) [exp[-(x-20)²/4Bt] + exp[-(x+20)²/4Bt]].
The position of maximum probability density as a function of time is obtained as xmax(t) = 20(1 - 2Bt/ln(4)).
(a) For the given diffusion differential equation au/a t = B(u) one-dimensional problem with no boundaries, the Green's function is given as
ƏG(x, t; 20,t) = 1/(2π) ∫ dk exp(-ik(x-20))exp(-k²Bt).
Taking Fourier transform of the equation gives
∂ G/ ∂ t = BG.
Substituting the Green's function in this equation and taking the Fourier transform of the function results in ∂G/ ∂ t = -k²BG.
This differential equation has the solution
G(x, t; 20, t) = 1/(4πBt) exp(-[(x-20)²/4Bt]),
which can be Fourier transformed back to the real space. Thus, the Green's function is obtained as
ƏG(x, t; 20,t) = 1/(2√πBt) exp[-(x-20)²/4Bt].
(b) If an absorbing wall is placed at x = 0, then the probability of finding a particle at x = 0 must be zero. The method of images can be used to solve this problem using the result from part (a).
The image source must be placed in the region x < 0. With the appropriate pre-factor, this image source can recreate the appropriate boundary conditions at x = 0.
Therefore, the Green's function for this case is obtained as
ƏG(x, t; 20,t) = 1/(2√πBt) [exp[-(x-20)²/4Bt] - exp[-(x+20)²/4Bt]].
(c) Using Fick's law j = -B(du/dx), where d is the concentration gradient, the rate of absorption at the wall can be found by considering the flux of particles at x = 0. At x = 0, the concentration gradient is given as
du/dx = (G(x, t; 20,t) - G(-x, t; 20,t))/2.
Substituting this into Fick's law and considering that j = -D du/dx at steady state, where D is the diffusion coefficient, gives the rate of absorption at the wall as
r = -D[B(∂G/∂x)]
x=0
r = (1/2)B[D/√πt](20/√Bt)²exp(-400Bt/4)
r = (5/2)B(20²/πt)exp(-100Bt).
therefore the required function is r = (5/2)B(20²/πt)exp(-100Bt).
(d) If the wall at x = 0 were reflecting, the flux of particles through the wall would be zero. But G(x=0) would not necessarily be zero. This is the boundary condition of the Neumann type, and the solution is unique.
The method of images can be used to find the Green's function. The image source must be placed in the region x < 0. With the appropriate pre-factor, this image source can recreate the appropriate boundary conditions at x = 0.
Therefore, the Green's function for this case is obtained as
ƏG(x, t; 20,t) = 1/(2√πBt) [exp[-(x-20)²/4Bt] + exp[-(x+20)²/4Bt]].
The position of maximum probability density as a function of time is obtained as xmax(t) = 20(1 - 2Bt/ln(4)).
learn more about Green's functions here:
https://brainly.com/question/3522546
#SPJ11
Please all the steps, one by one! How can this be solved?

Answers
There are 5 full square and 6 triangles that are half squares.
5 + (6)(1/2) = 5 + 3 = 8
You could also break this into smaller shapes (like a big triangle on the top and a smaller triangle and rectangle on the bottom and use area formulas to calculate the area. But counting works well in this example.


Answer: 8
Step-by-step explanation:
First you split up this shape into two different shapes, a triangle and trapezoid
Put a line through the coordinates (-2,2) to (-1,2); the top is a triangle and the other is a trapezoid
Area of the trapezoid is A = .5x (base1 + base2) x height
base1 of the trapezoid goes from -4 to -1 which is 3
base2 goes from -2 to -1 which is 1
height is 0 to 2 whcich is 2
A = .5 x (3+1) x 2 = 4
Now area of a triangle is A = .5 x base x height
the base goes from -2 to 2 which is 4
the height goes from 2 to 4 which is 2
A = .5 x (4) x (2) = 4
Area of the Trapezoid + Area of the Triangle = Total Area
4 + 4 = 8
Your friend has two standard decks of 52 playing cards and asks you to randomly draw one card from each deck. What is the probability that you will draw two eights
Answers
The probability of drawing two eights is 16/2,704, which simplifies to 1/169, or approximately 0.59%.
There are a total of 52 cards in each deck, so there are 52 x 52 = 2,704 possible combinations of cards that could be drawn.
To calculate the probability of drawing two eights, we need to determine the number of ways we can draw two eights and then divide that by the total number of possible combinations.
There are four eights in each deck, so there are 4 x 4 = 16 ways to draw two eights (one from each deck).
Therefore, the probability of drawing two eights is 16/2,704, which simplifies to 1/169, or approximately 0.59%.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
A forecasting method has produced the following over the past five months. What is the mean absolute deviation? 3. 6 3.8 3.2. \( 3.4 \) \( 3.0 \)
Answers
The mean absolute deviation for the given dataset of 3, 6, 3.8, 3.2, and 3.4 is approximately 0.996. This means that, on average, each data point in the dataset deviates from the mean by approximately 0.996.
The mean absolute deviation (MAD) measures the average distance between each data point and the mean of the dataset. To find the MAD, you need to follow these steps:
1. Calculate the mean of the dataset by adding up all the numbers and dividing the sum by the total number of data points. In this case, the dataset consists of the following numbers: 3, 6, 3.8, 3.2, and 3.4. Adding them up gives us a sum of 19.4. Dividing this sum by 5 (since there are 5 data points) gives us a mean of 3.88.
2. Find the absolute deviation for each data point by subtracting the mean from each data point and taking the absolute value. For example, for the first data point, 3, the absolute deviation would be |3 - 3.88| = 0.88. Repeat this step for all the data points.
3. Calculate the mean of the absolute deviations by adding up all the absolute deviations and dividing the sum by the total number of data points. In this case, the absolute deviations are: 0.88, 2.12, 0.72, 0.68, and 0.58. Adding them up gives us a sum of 4.98. Dividing this sum by 5 gives us a mean of 0.996.
So, the mean absolute deviation for the given dataset is approximately 0.996.
The mean absolute deviation helps us understand how much each data point varies from the mean of the dataset. By calculating the absolute deviation for each data point and finding the average, we can determine the typical amount of variation in the dataset.
The mean absolute deviation for the given dataset of 3, 6, 3.8, 3.2, and 3.4 is approximately 0.996. This means that, on average, each data point in the dataset deviates from the mean by approximately 0.996.
To know more about dataset visit ;
https://brainly.com/question/33387027
#SPJ11
Paulina plays both volleyball and soccer. The probability of her getting injured playing volleyball is 0. 10. 10, point, 1. The probability of her getting injured playing soccer is \dfrac{1}{10} 10
1
start fraction, 1, divided by, 10, end fraction
Answers
The probability of Paulina getting injured in either volleyball or soccer is 0.19.
To find the probability of Paulina getting injured in either volleyball or soccer, we can use the formula:
P(Volleyball or Soccer) = P(Volleyball) + P(Soccer) - P(Volleyball and Soccer)
We are given that the probability of Paulina getting injured playing volleyball is 0.1, and the probability of her getting injured playing soccer is 1/10 = 0.1 as well. However, we are not given any information about whether these events are independent or not, so we cannot assume that P(Volleyball and Soccer) is equal to the product of P(Volleyball) and P(Soccer).
If we assume that the events are independent, then we can calculate P(Volleyball and Soccer) as:
P(Volleyball and Soccer) = P(Volleyball) * P(Soccer) = 0.1 * 0.1 = 0.01
Then, using the formula above, we can calculate the probability of Paulina getting injured in either volleyball or soccer as:
P(Volleyball or Soccer) = 0.1 + 0.1 - 0.01 = 0.19
Therefore, the probability of Paulina getting injured in either volleyball or soccer is 0.19, assuming that the events are independent.
To know more about probability, refer to the link below:
https://brainly.com/question/29288787#
#SPJ11
I need help with this problem. Please show work and tell me if its one solution or all or none.
2x-y=9
2x+y=11
Answers
Answer:
x = 5, y = 1
Step-by-step explanation:
2x - y = 9
2x + y = 11 subtract equation 2 from equation 1
0 - 2y = -2
y = -2/-2 = 1 substitute into equation 1 or 2 to solve for x
2x - 1 = 9
2x = 10
x = 10/2 = 5
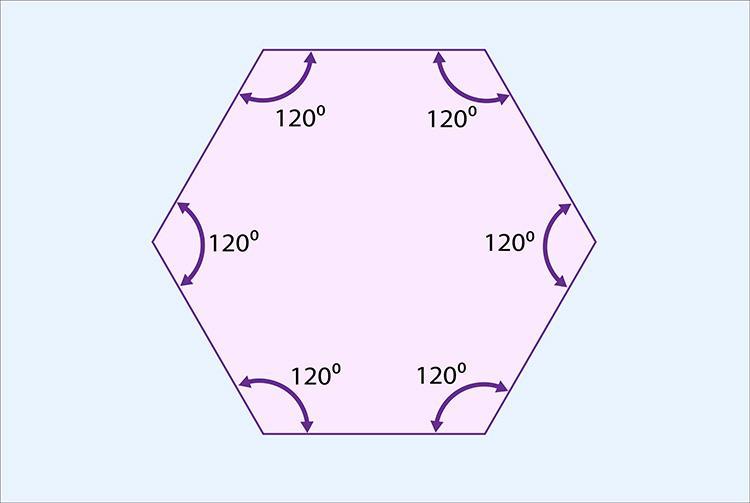
Find the sum of the interior angles for a hexagon. 540° 720° 900° 1,080°
Answers
The sum of interior Angles of Hexagon is always 720°
Any hexagon's internal angles add up to 720° in all cases. By dividing 720° by 6, we may get the size of each interior angle of a regular hexagon. As a result, we have:
720°÷6 = 120°
In a regular hexagon, each inside angle is 120°.
An example of a regular hexagon with equal-length sides and angles is shown in the diagram below. By multiplying the six 120° angles together, we can demonstrate that the result is 720°.
Therefore, the interior angles of a hexagon are always added up to 720°.
Learn more about hexagon :
brainly.com/question/3295271
#SPJ4
I need help with this please

Answers
Answer: y=-9.9
x has decreased by 3.3
x=9.9-3.3
=6.6
so you do the same to y
y=-6.6-3.3
=-9.9
How many ounces are in 4 pounds?
*
5 points
48 ounces
36 ounces
64 ounces
16 ounces
2. Divide: 1,111 ÷ 11 = ____________ (Write out)
*
5 points
11
111
101
110
3. Subtract: 6000 - 3,444= _______ ( write out)
*
5 points
2,456
2,656
2,556
2,655
4. Would a bottle of shampoo contain about 400ml or 400 liters?
*
5 points
400 ml
400 liters
5. Multiply: 3,540 x 9 = __________ ( write out to solve)
*
5 points
31,660
31,680
31,860
31,760
6. Any number multiplied by zero is equal to _____.
*
5 points
10
0
100
5
7. Mr. Williams left his house at 7:30. he drove for 4 hours and 20 minutes. At what time did he reach his destination? (hint: create a clock line.)
*
5 points
11:30
11:50
12:30
1:00
8. 7 x 6 = _______
*
5 points
13
42
54
49
9. Find the missing minuend. 92 - ____= 58
*
5 points
38
36
34
44
10. Subtract: $ 43.99 - $18.45= ________ (remember: Whenever you add or subtract using decimals, they MUST BE LINED UP.)
*
5 points
$25.45
$25.44
$25.54
$24.54
11. Divide: 4,842 ÷ 2= _________ (write out)
*
5 points
2,241
2,421
2,412
2,402
12. Multiply: 15 x 14 = _________ ( write out)
*
5 points
220
210
190
240
13. IF it is 11:50 now, what time was it 3 hours and 20 minutes ago? (hint: create a clock line.)
*
5 points
8:30
9:30
8:50
10:30
14. Find the estimated sum of 953 and 413.
*
5 points
≈1150
≈1350
≈1250
≈1500
15.Add: 5,218 + 6,970 = ________. (write out)
*
5 points
12, 218
12,178
12,188
13,168
16. Divide: 54 ÷ 9 = ____________. Hint: think related facts.
*
5 points
7
6
8
5
17. Arianna baby-sat from 7:00pm until 12:00 am. IF she earns $ 4.50 per hour for babysitting, how much did she earn? (multi-step. solve for the time first.)
*
5 points
$18.00
$20.50
$16.50
$22.50
18. Select a rectangle that shows 5/6 shaded.
*
5 points
A
B
C
D
19. Multiply: 12 x 3 = ______
*
5 points
24
36
18
46
20. A closed figure made up of three or more line segments that do not intersect is a _______________.
*
5 points
pentagon
polygon
hexagon
heptagon
Answers
am answering from two to ten

What is the distribution of B(s) + B(t), s ≤ s ≤ t,?
Answers
Therefore, the distribution of B(s) + B(t) is a normal distribution with mean 0 and variance 2(t - s).
The distribution of the sum of two independent Brownian motions, B(s) and B(t), where s ≤ t, is itself a normal distribution.
If we consider B(s) and B(t) as two random variables, each following a normal distribution with mean 0 and variance t - s, then their sum B(s) + B(t) will also follow a normal distribution. The mean of the sum will be 0 + 0 = 0, and the variance of the sum will be (t - s) + (t - s) = 2(t - s).
To know more about normal distribution,
https://brainly.com/question/29509087
#SPJ11
Jim and Krutika win some money and share it in the ratio 2:3. Jim gets £10. How much did Krutika get?
Answers
Answer:
£15
Step-by-step explanation:
The 2 part of the ratio represents the £10 that Jim gets.
Divide the amount by 2 to find the value of one part of the ratio.
£10 ÷ 2 = £5 ← value of 1 part of the ratio, thus
3 parts = 3 × £5 = £15 ← amount Krutika gets
The graph of the function C(x) = −0.74x2 + 22x + 75 is shown. The function models the production cost, C, in thousands of dollars for a tech company to manufacture a calculator, where x is the number of calculators produced, in thousands:
graph of a parabola opening down passing through points negative 4 and 57 hundredths comma zero, zero comma 62, 1 and 12 hundredths comma 75, 17 and 65 hundredths comma 167 and 55 hundredths, 34 and 18 hundredths comma 75, and 39 and 87 hundredths comma zero
If the company wants to keep its production costs under $175,000, then which constraint is reasonable for the model?
Answers
If the company wants to keep its production costs under $175,000, then 5.6 ≤ x ≤ 24.13 constraint is reasonable for the model given that the function C(x) = −0.74x² + 22x + 75 ,the production cost C, in thousands of dollars for a tech company to manufacture a calculator, where x is the number of calculators produced, in thousands. This can be obtained by using the given graph of the function.
Which constraint is reasonable for the model:A constraint is a condition of an optimization problem that should be satisfied the condition.
From the we have the function,
⇒ C(x) = −0.74x² + 22x + 75
the production cost C, in thousands of dollars for a tech company to manufacture a calculator, x is the number of calculators produced, in thousands.
In the graph the dotted line is the line where C(x) is $175,000. Above this line every the value is greater than $175,000.
The points where this line, that is C(x) = y = 175, intersect the graph of the given function C(x) = −0.74x² + 22x + 75 is (5.6, 175) and (24.13, 175).
This means that above the point (5.6, 175) the graph has the value greater than 175000 and below the point the graph has the value below 175000.Similarly, below the point (24.13, 175) the graph has the value greater than $175,000 and above the point the graph has the value below $175,000.Therefore, x ≥ 5.6 and x ≤ 24.13
⇒ 5.6 ≤ x ≤ 24.13
Hence if the company wants to keep its production costs under $175,000, then 5.6 ≤ x ≤ 24.13 constraint is reasonable for the model given that the function C(x) = −0.74x² + 22x + 75 ,the production cost C, in thousands of dollars for a tech company to manufacture a calculator, where x is the number of calculators produced, in thousands.
Learn more about constraints here:
brainly.com/question/12942108
#SPJ1

Answer:
0 ≤ x < 5.6 and 24.13 < x ≤ 32.82
Step-by-step explanation:
You have a mortagege of $275,000
after down payment with an interest
rate of 3% for 30 years.
What does P, r,n, and t are equal to?

Answers
Answer:
Our calculator limits your interest deduction to the interest payment that would be paid on a $1,000,000 mortgage. Interest rate: Annual interest rate for this
Step-by-step explanation:
what's a negative number greater than -10
Answers
Answer:
-1
Step-by-step explanation:
-2
-3 etc
thats the answer