Answers
Answer:
x = -2
y = 9
Step-by-step explanation:
y = -3x + 3
y = 5x + 19
We can put one y as another:
-3x + 3 = 5x + 19
-8x = 16
x = -2
And now let's check using x = -2
y = (-3 * -2) + 3
y = (5 * -2) + 19
y = 6 + 3
y = -10 + 19
y = 9
y = 9
Related Questions
If f(x)= x³ + 7x²-x and g(x)=x²-3, what is the degree of g(f(x))?
•2
•3
•6
•8
Answers
g(x) = x^2 - 3
f(x) = x^3+7x^2-x
Start with the g(x) function. Replace every x with f(x)
g(x) = x^2 - 3
g(f(x)) = ( f(x) )^2 - 3
Then replace the f(x) on the right side with x^3+7x^2-x
g(f(x)) = (x^3+7x^2-x)^2 - 3
The highest term inside the parenthesis is x^3. Squaring this leads to (x^3)^2 = x^(3*2) = x^6
So the highest exponent found in g(f(x)) is 6, meaning the degree of is 6
The first five multiples of the number 3
Answers
Answer: 3,6,9,12,15
Step-by-step explanation:
Im not sure how to explain this but if you listen to school house rock multiple of three song it helps.
PLEASE HELP. I need both the x and y and the length of DF

Answers
The value of x is 17, y is 2 and length of DF is 20.
Basic Proportionality Theorem (can be abbreviated as BPT) states that, if a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.
For x
DG = GE ( Given )
DG + GE = DE
DE = 2(DG)
DG/DE = 1/2
hence GH/EF = 1/2
By Basic Proportionality Theorem ( BPT )
(x – 3) / 28 = 1/2
after cross multiplication
2(x – 3) = 28
2x – 6 = 28
2x = 34
x = 17
For y
By Basic Proportionality Theorem (BPT) to side DF
DF = 2(DH)
DH/DF = 1/2
(y + 8) / (y + 8 + x – 7) = 1/2
after cross multiplication
2(y + 8) = y + 8 + x – 7
put x = 17
2(y + 8) = y + 8 + 17 – 7
2(y + 8) = y + 18
2y + 16 = y + 18
2y = y + 2
2y – y = 2
y = 2
DF = 2(2+8)
= 2(10)
= 20
Hence, x is 17, y is 2 and DF is 20.
To learn more about length here:
https://brainly.com/question/8552546
#SPJ1
there is a bag of marbles. inside the bag there are 10 blue marbles, 6 red marbles and 5 green marbles. two marbles are selected from the bag without replacement. what is the probability that neither of them are blue?
Answers
The probability that neither of the marbles selected is blue is 12/21.
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true.
In a bag of marbles, there are 10 blue marbles, 6 red marbles, and 5 green marbles.
Therefore, the total number of marbles in the bag is87:
= number of red marbles + blue marbles + green marbles
= 6 + 10 + 5
= 21
Now, two marbles are selected randomly without replacement.
So, the number of non-blue marbles is:
= number of red marbles + number of green marbles
= 6 + 5
= 11
Then, the probability that the two balls selected are not blue will be:
P( not blue ) = Number of non-blue marbles / Total number of balls in the bag
P( not blue ) = 12/21
Learn more about probability here:
brainly.com/question/13604758
#SPJ4
Determine the minimum rotation (in degrees) which will carry the following figure onto itself ( where all sides and verticles will match up). Round to the nearest tenth if necessary.
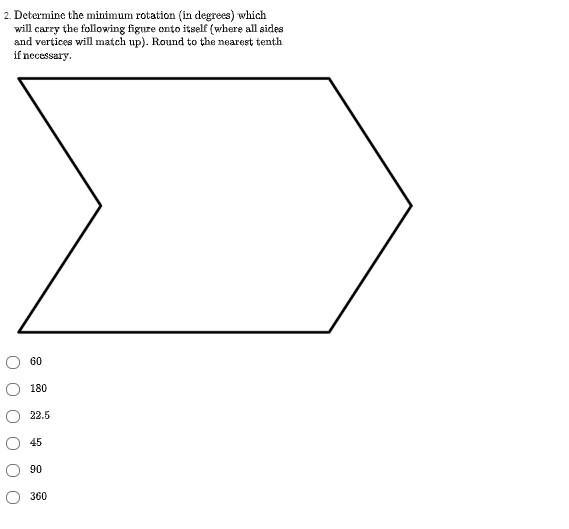
Answers
Answer:
360°
Step-by-step explanation:
The figure is irregular which means it must be completely rotated to have matching sides and vertices. A full rotation is equal to 360°.
What is the slope-intercept equation of the line below?

Answers
Answer:
C
Step-by-step explanation:
y=mx+b m=slope b=y-intercept, y-int: 4 slope: 3/1 but can just be put as 3. y=3x+4 bc it's a positive slope with a positive y-int.
An electric post casts a shadow of length 108 ft while a vertical rod of length 11 ft casts a shadow of length 18 ft. Find the length of the electric post.
Answers
The length of the electric post can be found using the concept of similar triangles. The ratio of the length of the electric post to the length of its shadow is equal to the ratio of the length of the vertical rod to the length of its shadow.
Let's denote the length of the electric post as x. According to the given information, the length of its shadow is 108 ft.
Using the proportion:
x/108 = 11/18
To solve for x, we cross-multiply:
18x = 108 * 11
Dividing both sides by 18:
x = (108 * 11) / 18
Calculating this, we find that the length of the electric post is approximately 66.67 ft.
To learn more about similar triangles: -brainly.com/question/14344804
#SPJ11
Kalyan Singhal Corp. makes three products, and it has three machines available as resources as given in the following LP problem: Maximize contribution = 3X₁ +5X₂ +7X3 1X₁ +7X₂ + 4X3 ≤ 100 2X1 + 1X₂ + 7X3 ≤ 110 8X₁ + 4X₂ + 1X3 ≤ 100 X₁, X2, X3 20 (C₁: hours on machine 1) (C₂: hours on machine 2) (C3: hours on machine 3) a) Using a computer software for solving LP, the optimal solution achieved is: (round your response to two decimal places). X₁² = X₂ = (round your response to two decimal places). = X3² (round your response to two decimal places). Contribution (objective value) = (round your response to two decimal places). b) Machine 1 has Machine 2 has Machine 3 has hours of unused time available at the optimal solution (round your response to two decimal places). hours of unused time available at the optimal solution (round your response to two decimal places). hours of unused time available at the optimal solution (round your response to two decimal places). dollars to the firm (round your response to two decimal places). c) An additional hour of time available for third machine, is worth d) An additional 5 hours of time available for the second machine, at no cost to the firm, are going to increase the objective value by dollars (round your response to two decimal places).
Answers
a) Contribution (objective value) = $132.14
b) The firm earns $132.14 at the optimal solution.
c) An additional hour of time available for the third machine is worth $0.14 to the firm.
d) An additional 5 hours of time available for the second machine will increase the objective value by $3.69.
The best result obtained from using computer software to solve the LP problem is: X1 = 11.43, X2 = 12.86, X3 = 5.71
b) The number of unused hours at the ideal solution is:
Machine 1 still has 8.57 hours of time left.
There are no hours left on Machine 2 at the moment.
There are still 94.29 hours left on Machine 3.
c) The shadow price of the third limitation is worth an extra hour of time available for the third machine. With the exception of increasing the right-hand side of the third constraint by one unit, we can solve the LP problem using the same constraints to determine the shadow price. Using LP to solve this issue, we discover that the shadow price for the third constraint is
For such more questions on optimal solution
https://brainly.com/question/31025731
#SPJ8
What is the part of line having 1 endpoint and extending in one direction?
Answers
A part of a line that has 1 endpoint and extends indefinitely in only one direction is called a ray.
A ray is named using its endpoint first, and then any other point on the ray
Properties of ray:
A line is a series of points placed together that continue infinitely.When this line is restricted from one direction and is extended in the other direction indefinitely, it forms a ray.It has just one starting point and does not have an opposite end and goes through and cuts many points and lines and is often used to draw angles, and we cannot measure the length of a ray.To know more about ray:
https://brainly.com/question/28045419
#SPJ4
You're running a one-sample t-test comparing your sample \( (M=40.6, S D=4.8) \) of 21 observations with a population that has \( \mu \) \( =39.8 \) at \( \alpha=0.01 \). Calculate \( t_{-} o b s \) ,
Answers
The value of \(t_{obs}\) is approximately equal to 3.47 (rounded off up to two decimal places)
Given the sample size, mean and standard deviation, to compute the one-sample t-test, we will use the formula:
\[t_{obs}=\frac{M-\mu}{\frac{s}{\sqrt{n}}}\]
Where, \(\mu\) is the population mean, M is the sample mean, s is the sample standard deviation, and n is the sample size.
Now, substituting the given values, we get,
\[t_{obs}=\frac{40.6-39.8}{\frac{4.8}{\sqrt{21}}}\]
Solving the above expression, we get
\[t_{obs}=3.4705\]
Thus, the value of \(t_{obs}\) is approximately equal to 3.47 (rounded off up to two decimal places).
Learn more about value from the given link
https://brainly.com/question/11546044
#SPJ11
wouldn’t it just be 94 degrees? please help

Answers
We know that the m<RTV = 65°.
If we know that the m<UTV = 29°, we can simply
subtract the m<UTV from the m<RTV to get the answer.
So we have 65 - 29 or 36°.
Two boats left the harbour at the same time. One travelled at 10km/h on a bearing N47degreeE. The other traveled at 8km/h on a bearing of N79degreeE. How far apart are the boats after 45min? Round the distance to nearest tenth of a km.
Answers
Answer:
4.0 km
Step-by-step explanation:
You want the distance between two boats after 45 minutes if they left at the same time and traveled 10 km/h at N47E, and 8 km/h at N79E.
Law of cosinesThe distances the boats traveled in 3/4 hour can be found by multiplying the speed by the time:
distance = speed · time
distance = {10 km/h, 8 km/h} · (3/4 h) = {7.5 km, 6 km}
The distance between their positions can be found from the law of cosines:
c² = a² +b² -2ab·cos(C)
Here, the angle between the vectors is 79° -47° = 32°, so the distance is given by ...
c² = 7.5² +6² -2·7.5·6·cos(32°) ≈ 15.925671
c ≈ √15.925671 ≈ 3.9907
To the nearest tenth km, the distance between the boats is 4.0 km.
__
Additional comment
It can be helpful to draw a diagram. A geometry app can measure the distance for you (attachment 1), or a calculator app can calculate it based on the speed vectors (attachment 2).


Whenever he visits Dayton, Quincy has to drive 12 miles due north from home. Whenever he
visits Belleville, he has to drive 16 miles due east from home. How far apart are Dayton and
Belleville, measured in a straight line?
Answers
Answer: 20 miles
Step-by-step explanation:
Hi, since the situation forms a right triangle (see attachment) we have to apply the Pythagorean Theorem:
x^2 = a^2 + b^2
Where x is the hypotenuse of the triangle (in this case the distance between Dayton and Belleville) and a and b are the other sides.
Replacing with the values given:
x^2 = 16^2 + 12^2
x^2 = 256+144
x^2 = 400
x = √400
x = 20 miles
Feel free to ask for more if needed or if you did not understand something.

Rebecca can do 150 jumping jacks in two minutes and Marcus can do 625 jumping jacks in eight minutes. who can do more jumping jacks per minute and by how much?
Answers
Answer:
Marcus can do more jumping jacks per minute.
Step-by-step explanation:
By 3 more jumping jacks.
Answer:
ryan can do the most
Step-by-step explanation:
by 3
pls help ty ty ty i need this ty

Answers
Answer:
52
Step-by-step explanation:
angles in a triangle add up to 180 so just subtract the angles to find the answer
Answer:
angle ABE = 52 degrees
Step-by-step explanation:

What is $2.75 in cents
Answers
100 times 2 is 200
200 plus 75 is 275
So it’s 275 cents
To convert dollar into cents, we need to multiply by 100. Thus, the total amount is equivalent to 275 cents.
Given:
Given amount is $ 2.75.
According to question, we have to convert currency of dollar into cents.
Conversion of amount from dollar to cent can be done as,
\(1\;\$=100\;\rm{cents}\\ \$\;2.75=\$\;\frac{275}{100}\\=\frac{275}{100}\times 100\;\rm{cents}\\=275\;\rm{cents}\)
Therefore, the total amount in cents is 275 cents.
Learn more about dollar to cent conversion here:
https://brainly.com/question/14790293
Solve using the quadratic formula.
9x to the exponent of two+ x - 9 = 0
Write your answers as integers, proper or improper fractions in simplest form, or decimals
rounded to the nearest hundredth.
Answers
Answer:
This is not really an answer but if you photomath and type in the problem for example “9x^2+x-9=0” you’ll be able to find your answer easily
Step-by-step explanation:
What is the product of -4 and 8.1?
A. -32.4
B. -12.1
C. 12.1
D. 32.4
Answers
Answer:
-32.4
Step-by-step explanation:
What you do is the -4 x the 8. after that you should get 32. Then you do 4 x the 1. Hence, you should get 4. Because of that you put the 32 and 4 together. your final answer is -32.4
Answer:
The answer is A. -32.4
Step-by-step explanation:
What you do is the -4 x the 8. after that you should get 32. Then you do 4 x the 1. Hence, you should get 4. Because of that you put the 32 and 4 together. your final answer is -32.4
Hope this helps :)
State whether the image below is an enlargement or a reduction identify the scale factor .

Answers
Answer:
enlargement, factor is 5
Step-by-step explanation:
if you multiply 5 to 3, 4,5 you get 15 20 25
Please help I will mark brainliest!

Answers
Answer:
9.
\(x \geqslant - 14\)
10. x<7
Baka naman answer me

Answers
Answer:
???
Step-by-step explanation:
Answer:SUS
Step-by-step explanation:
PLS HELP WILl MARK BRAiNLIEST

Answers
Step-by-step explanation:
draw a triangle then label corners a and b. spread them 120 degrees apart and there you have it.
use long or synthetic division to find the following quotients (w^3-2w^2-2w+1)÷(w-1)
Answers
The given polynimial exression is
(w^3-2w^2-2w+1)÷(w-1)
We wuld apply the long division method as shown below
The first step is todivide w^3 by w to give us w^2. w^2 is used to multiply w + 1 to give us w^3 + w^2 and this is subtracted from w^3 - 2w^2. The process continues until we cannot divide further. Thus, from the daigram above, the solution is
w^2 - 3w + 1

the laws of nature (as determined by scientists) group of answer choices are often written in the language of mathematics can never, ever change once they are written down in textbooks are constructed from many observations, hypotheses, and experiments more than one of these apply both on earth and among the stars
Answers
The laws of nature (as determined by scientists) are often written in the language of mathematics and are constructed from many observations, hypotheses, and experiments.
Mathematics provides a precise and rigorous language to describe the laws of nature. Scientists often express these laws in mathematical equations and formulas to convey their relationships and behaviors. The use of mathematics allows for accurate predictions, calculations, and further exploration of the laws of nature.
The laws of nature are not fixed or unchangeable once they are written down in textbooks. Scientific understanding and knowledge evolve over time as new observations, experiments, and hypotheses emerge. The laws of nature are continuously refined and expanded upon as scientists uncover new insights and gather more data. This iterative process of scientific inquiry leads to revisions and updates to our understanding of the laws of nature.
The laws of nature are constructed from many observations, hypotheses, and experiments. Scientists make systematic observations, form hypotheses to explain these observations, and then test them through experiments. The results of these experiments, along with further observations and data analysis, contribute to the development and refinement of the laws of nature. It is through this scientific process that our understanding of the natural world progresses.
Therefore, it is accurate to say that more than one of the provided answer choices apply to the laws of nature. They are often written in the language of mathematics and are constructed from many observations, hypotheses, and experiments. These principles apply not only on Earth but also among the stars, as scientists strive to understand the fundamental laws that govern the entire universe.
Learn more about hypotheses here:
brainly.com/question/33444525
#SPJ11
A 13-foot ladder is leaning against a wall. If the top slips down the wall at a rate of 2 ft/s, how fast will the foot be moving away from the wall when the top is 10 feet above the ground?
The foot will be moving at ___ ft/sec
Answers
Answer:
\(\frac{db}{dt}=\frac{20\sqrt{69}}{69}\approx2.4077\text{ ft/s}\)
Step-by-step explanation:
We know that the ladder is 13 feet long.
We also know that the top of the ladder is slipping down at a rate of 2ft/s.
And we want to find the rate at which the foot of the ladder is moving away when the top is 10 feet above the ground.
We can use the Pythagorean Theorem for this problem:
\(a^2+b^2=c^2\)
Let's let a be the leg by the wall, and b be the leg on the ground.
Our hypotenuse is 13 and it stays 13. So, let's substitute 13 for c:
\(a^2+b^2=(13)^2=169\)
Now, let's take the derivative of both sides with respect to t:
\(\frac{d}{dt}[a^2+b^2]=\frac{d}{dt}[169]\)
Evaluate. Use implicit differentiation:
\(2a\frac{da}{dt}+2b\frac{db}{dt}=0\)
We know that the top of the ladder is slipping down at a rate of 2ft/s. So, da/dt is -2 (it's negative because it's slipping downwards).
We want to find db/dt when the top is 10 feet above the ground. So, substitute 10 for a.
Since a is 10 and we know that c stays constant at 13, we can figure out b using the Pythagorean Theorem:
\(10^2+b^2=13^2\)
Evaluate:
\(100+b^2=169\)
Solve for b:
\(b^2=69\\b=\sqrt{69}\)
So, substitute -2 for da/dt, 10 for a, and √69 for db/dt. This yields:
\(2(10)(-2)+2(\sqrt{69})(\frac{db}{dt})=0\)
Solve for db/dt. Multiply:
\(-40+2(\sqrt{69})(\frac{db}{dt})=0\)
Add 40 to both sides:
\(2\sqrt{69}(\frac{db}{dt})=40\)
Divide both sides by 2√69:
\(\frac{db}{dt}=\frac{20}{\sqrt{69}}\)
Rationalize:
\(\frac{db}{dt}=\frac{20\sqrt{69}}{69}\approx2.4077\text{ ft/s}\)
So, the foot will be moving at approximately 2.4077 feet per second.
What is the difference between -10 and 10
Answers
Answer:
- 10 is negative and 10 is positive
Step-by-step explanation:
in integers,
-10 -9 -8 -7-6-5-4-3-2-1 0 1 2 3 4 5 6 7 8 9 10
Answer:
The difference between -10 an 10 is that, -10 is less than 0 and 10 is greater than 0.
Step-by-step explanation:
Which expression show 7+21 as a product of two facter's
Answers
Answer:
Expressing or writing 7+21 as a product of two factors requires the application of Distributive Property
The expression that shows 7+21 written as a product of two factors is
7(1 + 3).
To solve the above question, we apply the Distributive property.
This is expressed as:
a (b + c) = ab + ac
Where
a is the common factor
We are given the expression:
7 + 21
Splitting this into two factors using the distributive property
7 + 21
The common factor for 7 and 21 is 7
Hence, by factorising we have:
7 + 21 = 7(1 + 3)
Therefore, the expression that shows 7+21 written as a product of two factors is :
7(1 + 3)
Step-by-step explanation:
state the derivatives for the six inverse trigonometric functions. what study suggestions would you recommend for fellow students to learn these?
Answers
Derivative of six inverse trigonometric functions are as follow:
d/dx(sin⁻¹x) = 1 / √1 - x²
d/dx(cos⁻¹x) = -1 / √1 - x²
d/dx(tan⁻¹x) = 1 / √1 + x²
d/dx(cosec⁻¹x) = -1 / |x|√ x² - 1
d/dx(sec⁻¹x) = 1 / |x|√ x² -1
d/dx(cot⁻¹x) = -1 / √1 + x²
As given in the question,
Explanation of the derivative of six inverse trigonometric functions are as follow:
1. y = sin⁻¹x
⇒ x = siny
⇒d/dx(x) = d/dx(siny)
⇒ 1 = cosy dy/dx
⇒dy/dx = 1/cosy
⇒dy/dx = 1/√1-sin²y
⇒dy/dx = 1/√1-x²
⇒d/dx( sin⁻¹x) = 1/√1-x²
2. y = cos⁻¹x
⇒ x = cosy
⇒d/dx(x) = d/dx(cosy)
⇒ 1 =-siny dy/dx
⇒dy/dx = -1/siny
⇒dy/dx = -1/√1-cos²y
⇒dy/dx = -1/√1-x²
⇒d/dx( cos⁻¹x) = -1/√1-x²
3. y = tan⁻¹x
⇒ x = tany
⇒d/dx(x) = d/dx(tany)
⇒ 1 =sec²y dy/dx
⇒dy/dx = 1/sec²y
⇒dy/dx = 1/√1+ tan²y
⇒dy/dx = 1/√1 + x²
⇒d/dx( tan⁻¹x) = 1/√1+x²
4. y = cosec⁻¹x
⇒ x = cosecy
⇒d/dx(x) = d/dx(cosecy)
⇒ 1 =-cosecy coty dy/dx
⇒dy/dx = -1/cosecy coty
⇒dy/dx = -1/cosecy√cosec²y-1
⇒dy/dx = -1/|x|√x²-1
⇒d/dx( cosec⁻¹x) = -1/|x|√x²-1
5. y = sec⁻¹x
⇒ x = secy
⇒d/dx(x) = d/dx(secy)
⇒ 1 =secy tany dy/dx
⇒dy/dx = 1/secy tany
⇒dy/dx = 1/secy√sec²y-1
⇒dy/dx = 1/|x|√x²-1
⇒d/dx( sec⁻¹x) = 1/|x|√x²-1
6. y = cot⁻¹x
⇒ x =coty
⇒d/dx(x) = d/dx(coty)
⇒ 1 =-cosec²y dy/dx
⇒dy/dx = -1/cosec²y
⇒dy/dx = -1/√1+ cot²y
⇒dy/dx = -1/√1 + x²
⇒d/dx( cot⁻¹x) = -1/√1+x²
Therefore, the derivative of the six inverse trigonometric functions are given below:
d/dx(sin⁻¹x) = 1 / √1 - x²
d/dx(cos⁻¹x) = -1 / √1 - x²
d/dx(tan⁻¹x) = 1 / √1 + x²
d/dx(cosec⁻¹x) = -1 / |x|√ x² - 1
d/dx(sec⁻¹x) = 1 / |x|√ x² -1
d/dx(cot⁻¹x) = -1 / √1 + x²
Learn more about inverse trigonometric functions here
brainly.com/question/1143565
#SPJ4
I Need the answer and the steps

Answers
Answer:
perimeter=16root(5) mm
area=80 mm^2
Step-by-step explanation:
perimeter of a square is =4a=4*4root(5) mm
=16root(5) mm
area of a square is=a^2=(4root(5))^2=80 mm^2
Find the point on the terminal side of θ = -3π/4 that has an x coordinate of -1. Show your work, please
Answers
Answer:
Step-by-step explanation:
\(-\frac{3\pi}{4}\) is the same as -135°. Since positive angles are measured counterclockwise, and this one is negative, we are measured clockwise. Doing that puts us into the second quadrant where both x and y are negative. The terminal side of the angle is the side that is free to move and open and close the angles. The initial side is the one that is on the positive x-axis and does not move. We are looking for a point on the terminal side of that angle, which means we are looking for the (x, y) coordinate on that point where x = -1.
Now...between the negative x-axis and the terminal side of the angle is a 45°. That's what's important here. From the origin we move left along the negative x-axis to -1. From that point we can drop an altitude to meet the terminal side and have created a right triangle in the process. Where the altitude meets the terminal side is the point (-1, y) that we are looking for.
Now comes the point in your work where you need to remember the Pythagorean triple for a 45-45-90 triangle. On a unit circle, everything is based on 1 unit, and the side length across from a 45 degree angle is 1. In our case, because we are in the second quadrant, both the side lengths across from both of those angles will be 1 and they will both be negative. That means that the point on the terminal side of that angle is (-1, -1).
