You weigh a random sample of adult golden retrievers and get the following results: 55, 64, 58, 61, 69, 64, 59, 69, 72, and 65. Which answer gives a 98% confidence interval for the mean of the population
Answers
Answer:
The 98% confidence interval for the mean of the population is (59, 68.2).
Step-by-step explanation:
Before building the confidence interval, we need to find the sample mean and the sample standard deviation.
Sample mean:
\(\overline{x} = \frac{55+64+58+61+69+64+59+69+72+65}{10} = 63.6\)
Sample standard deviation:
\(s = \sqrt{\frac{(55-63.6)^2+(64-63.6)^2+(58-63.6)^2+(61-63.6)^2+(69-63.6)^2+(64-63.6)^2+(59-63.6)^2+(69-63.6)^2+(72-63.6)^2+(65-63.6)^2}{10}} = 5.142\)
Confidence interval:
We have the standard deviation for the sample, and thus, we use the t-distribution.
The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So
df = 10 - 1 = 9
98% confidence interval
Now, we have to find a value of T, which is found looking at the t table, with 9 degrees of freedom(y-axis) and a confidence level of \(1 - \frac{1 - 0.98}{2} = 0.99\). So we have T = 2.821
The margin of error is:
\(M = T\frac{s}{\sqrt{n}} = 2.821\frac{5.142}{\sqrt{10}} = 4.6\)
In which s is the standard deviation of the sample and n is the size of the sample.
The lower end of the interval is the sample mean subtracted by M. So it is 63.6 - 4.6 = 59
The upper end of the interval is the sample mean added to M. So it is 63.6 + 4.6 = 68.2.
The 98% confidence interval for the mean of the population is (59, 68.2).
Related Questions
A cake recipe calls for the following dry ingredients: 3 ½ cups of flour, 2 ⅔ cups of sugar, and 1 ¾ cups of cocoa. To the nearest cup, how much dry ingredients will be used?
HELO
Answers
The amount of dry ingredients used in the cake recipe is approximately 7 cups.
We have,
3 ½ cups of flour, 2 ⅔ cups of sugar, and 1 ¾ cups of cocoa.
Now, first convert all quantity in same unit.
3 ½ cups of flour
= 3 cups + 0.5 cups
= 3 cups and 8 ounces.
and, 2 ⅔ cups of sugar
= 2 cups + 0.67 cups,
= 2 cups and 10.72 ounces.
and, 1 ¾ cups of cocoa
=1 cup + 0.75 cups
= 1 cup and 12 ounces.
So, the total amount
= 3 cups and 8 ounces + 2 cups and 10.72 ounces + 1 cup and 12 ounces = 6 cups and 14.72 ounces
= 7 cups
Therefore, the amount of dry ingredients used in the cake recipe is approximately 7 cups.
Learn more about Unit Conversion here:
https://brainly.com/question/19420601
#SPJ1
HELPPPPPPPPPPPPPPPPPPP

Answers
Answer:
simple.
Step-by-step explanation:
If you know the angle of a straight line, its 180. first, subtract 180-135. this wqould be 45. therefore, the interior angle is 45. We know that a triangles area always adds to 180, so it would be 45+x+74=180. this would be x=61. to check, add the same thing, 45+74, but instead of x add 61.
When ordering the Kids' Lunch at Burger Universe, the customer must choose a size, a type of bun, a side order, and a type of fruit drink. Here are the possibilities for each choice. Choice Possibilities Size: junior, Small, Medium, Large Type of bun Plain bun, Sesame seed bun Side order Fries, Onion rings Fruit drink Orange, Grape, Cherry, Lemonade How many Kids' Lunches are possible?
Answers
The number of Kid's Launches that are possible is 128. This is solved using Combination Principle.
What is combination in Math?A combination in mathematics is a selection of elements from a set with distinct members, where the order of selection is irrelevant.
Hence,
The number of possible "Sizes" from the specified 4 sizes are ⁴C₁
The number of sorts of bun that is possible from the specified two bun types is: ²C₁
From the four sides, the number of possible side purchases is: ⁴C₁
Of the available four drinks, the number of the possible drinks is: ⁴C₁
Now the possible number of all lunches are:
⁴C₁ x ²C₁ x ⁴C₁ x ⁴C₁
= 4 x 2 x 4 x 4
= 128
Hence the number of Kid's Lunches that are possible are 128.
Learn more about combination:
https://brainly.com/question/20211959
#SPJ1
What is the surface area of the prism shown below? Show all of your work. 12 ft. 13 ft. 14 ft.
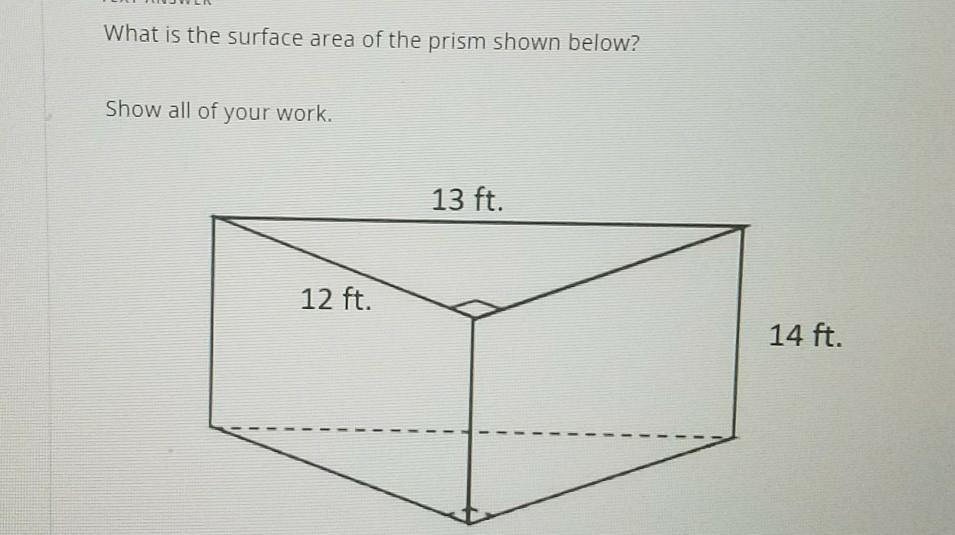
Answers
Step-by-step explanation:
1/2×13×12= 78
12×14= 132
13×14= 182
total surface area
= (78×2)+(132×2)+182
= 602 ft^2
work this out 8.26 + 2 =
a. 4.13
b.5.13
c.5.20
Answers
Answer:
10.26
Step-by-step explanation:
This is the answer because:
1) 8 + 2 = 10
2) Now, just add .26 to 10 which is 10.26
Hope this helps! :D
find KP in simplest radical form id K(5,6) and P(1, -4)

Answers
Answer:
move over 5 to the right and 6 up
move 1 to the right and 4 down to get your answer
Amplitude is ______.
the maximum displacement of a function on a graph
the minimum displacement of a function on a graph
Answers
Amplitude is the maximum displacement of a function on a graph.
What is amplitude?
Amplitude is the maximum displacement of a function on a graph. It refers to the maximum height or distance from the baseline of a wave or oscillation.
It is often used in physics and engineering to describe the strength or size of a signal, vibration, or wave. In simple terms, it can be thought of as the "peak-to-peak" distance of a waveform, or the height of the waveform above and below the baseline.
But the minimum displacement of a function on a graph would typically be referred to as the minimum value or the "valley" of the function.
Learn more about amplitude on:
https://brainly.com/question/25699025
#SPJ1
60 points!
solve 60 points!
It takes a shipping employee 4.25 min to prepare a package for domestic delivery and 6.5 min to prepare a package for international delivery.
Let x represent the number of domestic packages.
Let y represent the number of international packages.
The employee has no more than 1 h to ship packages.
The employee must ship more than 10 packages.
Select all correct choices for the inequalities that model these constraints.
4. 25x + 6.57 < 60
y>0
4. 25x + 6.5y > 60
x+ y< 10
x+y > 10
x > 0

Answers
Answer:
4.25x + 6.5y ≤ 60
y ≥ 0
x + y > 10
x ≥ 0
Step-by-step explanation:
We will write mathematical inequalities for all the details given.
Let x represent the number of domestic packages.
We cannot have negative packages, so x ≥ 0.
Let y represent the number of international packages.
We cannot have negative packages, so y ≥ 0.
The employee has no more than 1 h to ship packages.
If it takes 4.25 minutes to prepare an x package and 6.5 minutes to prepare a y package, and 1 hour is equal to 60 minutes, we can write this as 4.25x + 6.5y ≤ 60.
The employee must ship more than 10 packages.
This means the total number of packages must be greater than 10, so x + y > 10.
A hacker is trying to guess someone's password. The hacker knows (somehow) that the password is 9 characters long, and that each character is either a lowercase letter, (a, b, c, etc.), an uppercase letter (A, B, C, etc.) or a numerical digit (0, 1, 2, 3, 4, 5, 6, 7, 8, or 9). Assume that the hacker makes random guesses. What is the probability that the hacker guesses the password on his first try? Enter your answer as a decimal or a fraction, not a percentage.
Answers
The probability that the hacker guesses the password on their first try is extremely low.
What is the probability that the hacker guesses the password on his first try?
There are 26 lowercase letters, 26 uppercase letters, and 10 numerical digits, for a total of 62 possible characters for each position in the password. Since the password is 9 characters long, there are \(62^{9}\) possible passwords.
The probability that the hacker guesses the password on their first try is 1 out of the total number of possible passwords:
Probability = 1 / (\(62^{9}\))
Using a calculator, this can be simplified to approximately 1.2 x \(10^{-16}\)
Therefore, the probability that the hacker guesses the password on their first try is extremely low.
to know more about probability
brainly.com/question/30034780
#SPJ1
2x+10= 5x-17 hurry is for a test
Answers
Explanation
Answer:
X is 9
Step-by-step explanation:
Simplify n ⋅ n⋅ 2n
someone please help thanks
Answers
Answer:
the answer would be:
\(2n^3\)
Hope that helps! :)
Step-by-step explanation:
Prove that Newton-Raphson method for solving the equation \(x^{k} e^{x} = 0\) (where k is constant) is given by this formula: \(x _{n +1} = \frac{(K-1)x_n + x_n^{2} }{K+x_n}\)
Answers
We have proved that the Newton-Raphson iteration formula for solving the equation\(x^k e^x = 0\) is given by \(x_{n+1} = (k - 1) x_n + x_n^2 / k + x_n.\)
To prove that the Newton-Raphson method for solving the equation \(x^k e^x = 0\), where k is a constant, is given by the formula
\(x_{n+1} = (k - 1) x_n + x_n^2 / k + x_n,\)
we can start by considering the iterative process of the Newton-Raphson method.
Given an initial guess \(x_n\), we want to find a better approximation \(x_{n+1}\)that is closer to the root of the equation \(x^k e^x = 0.\)
The Newton-Raphson method involves the following steps:
Calculate the function value \(f(x_n) = x_n^k e^x_n\) and its derivative \(f'(x_n) = k x_n^(k-1) e^x_n.\)
Find the next approximation x_{n+1} by using the formula:
\(x_{n+1} = x_n - f(x_n) / f'(x_n)\)
Let's apply these steps to our equation \(x^k e^x = 0\):
Calculate the function value and its derivative:
\(f(x_n) = x_n^k e^x_n\\f'(x_n) = k x_n^(k-1) e^x_n\)
Find the next approximation x_{n+1} using the formula:
\(x_{n+1} = x_n - f(x_n) / f'(x_n)\)
Substituting the function value and its derivative:
\(x_{n+1} = x_n - (x_n^k e^x_n) / (k x_n^(k-1) e^x_n)\\= x_n - (x_n^k / k)\)
Simplifying the expression by combining like terms:
\(x_{n+1} = x_n - (x_n^k / k)\\= x_n - x_n^k / k\\= (k - 1) x_n + x_n^2 / k + x_n\)
Therefore, we have proved that the Newton-Raphson iteration formula for solving the equation\(x^k e^x = 0\) is given by \(x_{n+1} = (k - 1) x_n + x_n^2 / k + x_n.\)
for such more question on Newton-Raphson iteration
https://brainly.com/question/17150870
#SPJ8
If IK=JK, find mlJ
A. 72°
B. 82°
C. 122°
D. 134°
Answers
Answer:
D.134
Step-by-step explanation:
The side lengths of a triangle are 12, 19, and x units.
12
19
(The figure above gives only one possible configuration for the triangle.)
Determine the possible values of x.
Write your answer as an inequality.
Use x only once in your inequality.
D>
ISO
D20
Х
?

Answers
Answer:
7<x<31
Step-by-step explanation:
The third side of any triangle must be more than the difference between the other two sides.
x>19-12
x>7 (or) 7<x
The third side of any triangle must be less than the sum of the other two sides.
x<19+12
x<31 (or) 31>x
Put them together.
7<x<31 (or) 31>x>7
7<x<31 are the possible values of x.
What is Triangle?A triangle is a three-sided polygon that consists of three edges and three vertices.
Given that side lengths of a triangle are 12, 19, and x units.
We need to find the value of x.
We know that the third side of any triangle must be more than the difference between the other two sides.
x is greater than difference of nineteen and twelve
x>19-12
x>7 (or) 7<x
The third side of any triangle must be less than the sum of the other two sides.
x<19+12
x<31 (or) 31>x
From this we get the interval as
7<x<31 (or) 31>x>7
Hence, 7<x<31 are the possible values of x.
To learn more on Triangles click:
https://brainly.com/question/2773823
#SPJ2
5(−2) + (2−)2
when =3 and =−2
Answers
Answer:
36 is the final value for the equation you posted
Step-by-step explanation:
We are told that = 3 and = −2.
Let's plug these values into the equation.
= (5 ( − 2) + (2 − )^2)
= (5 (3 − 2(−2)) + (2 − 3)^2)
= (5 (3 + 4) + (−1)^2)
= (5 (7) + 1)
= 35 + 1
= 36
A rectangular metal tank with an open top is to hold cubic feet of liquid. What are the dimensions of the tank that require the least material to%E2%80%8B build?
Answers
Answer:
\(h = 3.5\)
\(w = 7\)
\(l = 7\)
Step-by-step explanation:
Given
\(Volume = 171.5ft^3\)
Required
The dimension that requires least material
The volume is:
\(Volume = lwh\)
Where:
\(l \to length\)
\(w \to width\)
\(h \to height\)
So, we have:
\(171.5 = lwh\)
Make l the subject
\(l = \frac{171.5}{wh}\)
The surface area (A) of an open-top rectangular tank is:
\(A = lw + 2lh + 2wh\)
Substitute: \(l = \frac{171.5}{wh}\)
\(A = \frac{171.5}{wh} * w + 2*\frac{171.5}{wh}*h + 2wh\)
\(A = \frac{171.5}{h} + 2*\frac{171.5}{w} + 2wh\)
\(A = \frac{171.5}{h} + \frac{343}{w} + 2wh\)
Rewrite as:
\(A = 171.5h^{-1} + 343w^{-1} + 2wh\)
Differentiate with respect to h and w
\(A_h = -171.5h^{-2} +2w\)
\(A_w = -343w^{-2} +2h\)
Equate both to 0
\(-171.5h^{-2} +2w=0\)
Make w the subject
\(2w = 171.5h^{-2}\)
Divide by 2
\(w = 85.75h^{-2}\)
\(-343w^{-2} +2h = 0\)
Make h the subject
\(2h = 343w^{-2}\)
Divide by 2
\(h = 171.5w^{-2}\)
\(h = \frac{171.5}{w^2}\)
Substitute \(w = 85.75h^{-2}\) in \(h = \frac{171.5}{w^2}\)
\(h = \frac{171.5}{(85.75h^{-2})^2}\)
\(h = \frac{171.5}{85.75^2*h^{-4}}\)
\(h = \frac{2}{85.75*h^{-4}}\)
Multiply both sides by \(h^{-4}\)
\(h^{-4} * h = \frac{1}{85.75*h^{-4}} * h^{-4}\)
\(h^{-3} = \frac{2}{85.75}\)
Rewrite as:
\(\frac{1}{h^3} = \frac{2}{85.75}\)
Inverse both sides
\(h^3 = 85.75/2\)
\(h^3 = 42.875\)
Take cube roots
\(h = 3.5\) ---- height
Recall that: \(w = 85.75h^{-2}\)
\(w = 85.75 * 3.5^{-2}\)
\(w = 7\) --- width
Recall that: \(l = \frac{171.5}{wh}\)
\(l = \frac{171.5}{3.5 * 7}\)
\(l = 7\) --- length
For a project in her Geometry class, Deepa uses a mirror on the ground to measure the height of her school’s football goalpost. She walks a distance of 9.35 meters from the goalpost, then places a mirror on flat on the ground, marked with an X at the center. She then steps 6.95 meters to the other side of the mirror, until she can see the top of the goalpost clearly marked in the X. Her partner measures the distance from her eyes to the ground to be 1.35 meters. How tall is the goalpost? Round your answer to the nearest hundredth of a meter.
Answers
Deepa makes use of the geometric property of similar triangles formed by
incident and reflected rays to determine the height of the goalpost.
The height of the goalpost is approximately 1.82 metersReasons:
When an object is reflected on a mirror, the angle of incidence, θ₁ is equal
to the angle of reflection, θ₂.
θ₁ = θ₂
Given that the angle, ∅₁, the incident ray of light and the angle, ∅₂, the
reflected light make with horizontal are both complementary angles, to the
angle of incident and reflection, respectively, we have;
θ₁ + ∅₁ = θ₂ + ∅₂
θ₁ = θ₂
Therefore, by subtraction property of equality, we have;
∅₁ = ∅₂
The vertical line from the top of the goalpost to the base of the goalpost
and the the vertical line from Deepa's eyes to the ground on which her feet
is standing are both perpendicular to the ground, therefore, the light from
the top of the goalpost to the mirror and to her eyes form similar triangles
by Angle Angle similarity postulate, which gives;
\(\displaystyle \frac{6.95}{9.35} = \frac{1.35}{The \ height \ of \ the \ goalpost}\)
6.95 × Height of the goalpost = 1.35 × 9.35
\(\displaystyle Height \ of \ the \ goalpost = \frac{1.35 \ m \times 9.35 \ m}{6.95 \ m} \approx 1.82 \ m\)
The height of the goalpost is approximately 1.82 meters.
Learn more here:
https://brainly.com/question/15268683

find the inverse of each equation

Answers
The inverse of the equation is determined as \(y = \log_{6}(-3x)\).
option D is the correct answer.
What is the inverse of the equation?The inverse of the equation is calculated by applying the following method;
The given equation;
y = - 6ˣ/3
The inverse of the equation is calculated as;
multiply through by 3
\(-3x = 6^y\)
Take the logarithm of both sides of the equation with base -6:
\(\log_{6}(-3x) = y\)
Finally, replace y with x to obtain the inverse equation as follows;
\(y = \log_{6}(-3x)\)
Learn more about inverse of equation here: https://brainly.com/question/29390335
#SPJ1
Solve the following system of equations graphically and check
3x - y = 3
Y=2x-7
Answers
Answer:
x = -4 and y = -15
Hope This Helps!!!
Choose the expression which represents the phrase, “the sum of 12 and a number H”

Answers
Answer:
the correct answer is option C
Answer:
Hello There!!
Step-by-step explanation:
The answer is c. 12+h as sum means adding 12 and then with h.
hope this helps,have a great day!!
~Pinky~
Let X be a binomial random variable with parameters (n, p). Find the approximate value of P(|X| > a) when n is sufficiently large using the central limit theorem, where a is a positive number. g
Answers
Answer:
Approximate value of P(|X| > a) is attached below
Ф ( 0 ) is the CDF of standard Normal variate
Step-by-step explanation:
x ~ Bin ( n, p )
E ( x ) = np , Var ( x ) = np ( 1 - p )
∴ Z = Iin ( x - E(x) ) / √Var x ) ~ N ( 0, 1 ) ( this is the standard normal Variate)
n-1∞
Find the approximate value of P(|X| > a)
Ф ( 0 ) is the CDF of standard Normal variate
attached below is the remaining part of the solution

what is -35 − (-12) =
Answers
Answer:
- 23
Step-by-step explanation:
When you see a negative number behind a minus sign, turn the minus sign into a plus sign. It's the easiest way to figure out how to solve those types of problems.
Answer:
-23
Step-by-step explanation:
-35-(-12) = -35+12 = -23
The values in the table represent a function.
A 2-column table with 5 rows. The first column is labeled x with entries negative 6, 7, 4, 3, negative 5. The second column is labeled f of x with entries 8, 3, negative 5, negative 2, 12.
Use the drop-down menus to complete the statements.
The ordered pair given in the first row of the table can be written using function notation as
.
f(3) is
.
f(x) = –5 when x is
.
Answers
The correct answers are:
f(-6) = 8f(3) = -2f(x) = -5 when x is 4What is the function?Functions are expressions separated by an equal sign. They have both dependent and independent variables.
How to solve* Lets explain how to solve the problem
- The table of the function has two column
# First column labeled x with entries:
-6 , 7 , 4 , 3 , -5
# Second column labeled f(x) with entries:
8 , 3 , -5 , -2 , 12
∴ The ordered pairs of the function f(x) are:
(-6 , 8) , (7 , 3) , (4 , -5) , (3 , -2) , (-5 , 12)
* Lets complete the missing
∵ The value of x in the first row is -6
∵ The value of f(x) in the first row is 8
∴ The function notation in the 1st row is f(-6) = 8
- The ordered pair given in the first row of the table can be
written using function notation as f(-6) = 8
∵ The ordered pair whose x = 3 is (3 , -2)
∴ The value of f(x) when x = 3 is -2
∴ f(3) = -2
∵ The ordered pair whose f(x) = -5 is (4 , -5)
∴ The value of x when f(x) = -5 is 4
∴ f(x) = -5 when x is 4
To learn more about the function visit, https://brainly.com/question/28278690
-2=g-9
one step equation!

Answers
Hope it's helpful!!
Complete the equation of the line through
(
−
6
,
5
)
(−6,5)left parenthesis, minus, 6, comma, 5, right parenthesis and
(
−
3
,
−
3
)
(−3,−3)left parenthesis, minus, 3, comma, minus, 3, right parenthesis.
Answers
The line that goes between the coordinates (-6, 5) & (-3, -3) has the equation y = -8/3 x + 13, as stated in the question.
What does a math line mean?A line is an infinitely long, completely straight, one-dimensional form that has no thickness and may be drawn in both directions. In order to stress that a line has no "flutters" anywhere along its length, it is occasionally referred to as a straight line or, more formally, a straight line (Casey 1893).
y - y1 = m (x - x1)
By using formula :
m = (y2 – y1) / (x2 - x1)
In other (x1, Y1)& are the two pairs on the line (x2, y2).
m = ( -3 - 5) / (-3 - (-6)) = (-8) / (-3 + 6) = -8 / 3
Due to this reason, the line has a slope of -8/3.
Afterwards when, we may input either points (-6, 5) and slope (8/3), respectively, into the generate the result of both the line to obtain:
y - 5 = -8/3 (x - (-6))
Expanding the right-hand side, we get:
y - 5 = -8/3 x + 8
Finally, rearranging the terms, we get:
y = -8/3 x + 8 + 5
y = -8/3 x + 13
Consequently, the line's equation becomes y = -8/3 x + 13 and it passes through to the coordinates (-6, 5) & (-3, -3).
To know more about line, visit
brainly.com/question/20299920
#SPJ1
The complete question is: Complete the equation of the line through (-6,5)(−6,5)left parenthesis, minus, 6, comma, 5, right parenthesis and (-3,-3)(−3,−3)left parenthesis, minus, 3, comma, minus, 3, right parenthesis.
yessssssssssssss sirrrrrr
Answers
125x ^ 3 - 27 = 0
Solve this by grouping
Answers
The solution to the equation 125x³ - 27 = 0 is (5x−3)(25x ^2 +15x+9)
What is an equation?An equation is a mathematical expression that contains an equals symbol. Equations often contain algebra. Algebra is used in mathematics when you do not know the exact number in a calculationsolving the equation 125x³ - 27 = 0 by grouping
Rewriting 125x^ 3 −27 as (5x) ^3 −3³
The difference of cubes can be factored using the rule:: a ^3 −b^ 3 =(a−b)(a^ 2 +ab+b^ 2 )
Polynomial 25x^ 2 +15x+9 is not factored since it does not have any rational roots.
Hence, (5x−3)(25x ^2 +15x+9)
Learn more about equation at:
https://brainly.com/question/25976025
#SPJ1
Use the approach in Gauss's problem to find the sums of the arithmetic sequences below(do not use formulas).e without aa. 1+ 2+ 3+ 4 + ... +39b. 1+3+5 + 7 + ... + 2409c. 3+ 6 + 9 + ... + 300d. 1000 +995 +990 + ... + 5a. The sum of the sequence is
Answers
Gauss's approach consists in group highest terms with lowest terms
a. 1+ 2+ 3+ 4 + ... +39
(1 + 39) + (2+38) + (3+37) + ... + (19+21) + 20
There are 19 terms in parentheses, all equal to 40. Then, the sum is equal to:
19*40 + 20 = 780
b. 1+3+5 + 7 + ... + 2409
(1+2409) + (3+2407) + (5+2405) + ... + (1203+1207) + 1205
there are (1203+1)/2 = 602 terms equal to 2410. Then, the sum is equal to:
602*2410 + 1205 = 1452025
c. 3+ 6 + 9 + ... + 300
(3+297) + (6+294) + (9+291) + ... + (147+153) + 150 + 300
there are 147/3 = 49 terms equal to 300. Then, the sum is equal to:
49*300 + 150 + 300 = 15150
d. 1000 +995 +990 + ... + 5
1000 + (995+5) + (990+10) + ... + (505+495) + 500
the sum has 1000/5 = 200 terms, then there are 99 terms in parentheses, all of them equal to 1000. Then, the sum is equal to:
1000 + 99*1000 + 500 = 100500
I am stuck please help!
Rewrite the equation below so that it does not have fractions.
5/9x-7=2/3
do not use decimals
Answers
Answer:
5x - 63 = 6
Step-by-step explanation:
Okay, first step, let's get all fractions having a common denominator, to do this, multiply 2/3 by 3 to get 6/9. Now, we have 5/9x-7=6/9. To make these into whole numbers, we can multiply the whole equation by the denominator (9). 5/9x multiplied by 9 is 5. 7 multiplied by 9 is 63. 6/9 multiplied by 9 is 6. Now we have 5x-63=6. If I were to simplify the equation, it would require decimals, so I'll leave it at this, but the equation simplified is x=13.8.
A line that includes the points (-8, f) and (-6, 4) has a slope of 6. What is the value of f?
f =?
Answers
Answer:
-8
Step-by-step explanation:
Slope = (y1-y2) / ( x1-x2)
= ( f-4) / (-8 - -6) = 6
(f-4) / -2 = 6
f-4 = -12
f = - 8
Answer:
f = -8
Explanation:
Find slope:
\(\sf slope: \dfrac{y_2 - y_1}{x_2- x_1} = \dfrac{\triangle y}{\triangle x} \ \ where \ (x_1 , \ y_1), ( x_2 , \ y_2) \ are \ points\)
Here given:
points: (-8, f), (-6, 4)slope : 6Inserting into slope formula:
\(\sf \rightarrow \dfrac{4-f}{-6-(-8) } = 6\)
\(\sf \rightarrow \dfrac{4-f}{2 } = 6\)
\(\sf \rightarrow 4-f = 12\)
\(\sf \rightarrow -f = 12-4\)
\(\sf \rightarrow -f =8\)
\(\sf \rightarrow f =-8\)