(x+9)(x+2)=4(x+9) what is the value ofx
Answers
Answer:
x = - 9, x = 2
Step-by-step explanation:
Given
(x + 9)(x + 2) = 4(x + 9) ← expand factors on left using FOIL
x² + 11x + 18 = 4x + 36 ( subtract 4x + 36 from both sides )
x² + 7x - 18 = 0 ← in standard form
(x + 9)(x - 2) = 0 ← in factored form
Equate each factor to zero and solve for x
x + 9 = 0 ⇒ x = - 9
x - 2 = 0 ⇒ x = 2
Related Questions
Pls help I’ll mark as brainliest!!

Answers
Answer:
Option 1
Step-by-step explanation:
(a-√a/√a-1) - (√a+1/a+√a) : √a+1/a. solve a
Answers
Answer:
Step-by-step explanation:
\(\displaystyle \ \Large \boldsymbol{} \frac{a-\sqrt{a} }{\sqrt{a}-1 } -\frac{\sqrt{a}+1 }{a+\sqrt{a} } :\frac{\sqrt{a}+1 }{a} = \\\\\\\frac{\sqrt{a}(\sqrt{a} -1 ) }{(\sqrt{a}-1) } -\frac{\sqrt{a}+1 }{\sqrt{a}(\sqrt{a}+1 )}\cdot \frac{\sqrt{a}\cdot \sqrt{a} }{\sqrt{a}+1 } = \\\\\\\sqrt{a} -\frac{\sqrt{a} }{1+\sqrt{a} } =\frac{a+\sqrt{a}-\sqrt{a} }{1+\sqrt{a} } = \\\\\\\frac{a}{\sqrt{a}+1 } \cdot \frac{\sqrt{a}-1 }{\sqrt{a}-1} } =\boxed{\frac{a\sqrt{a} -a}{a-1} }\)
(2x^3+x^2+25) divided by (2x+5),use long division to find the quotient
Answers
Step 1: Divide the leading term of the dividend by the leading term of the divisor.
2x^3 / 2x = x^2
Step 2: Multiply the divisor by the quotient obtained in Step 1.
(x^2)(2x + 5) = 2x^3 + 5x^2
Step 3: Subtract the result obtained in Step 2 from the dividend.
(2x^3 + x^2 + 0x + 25) - (2x^3 + 5x^2) = -4x^2 + 0x + 25
Step 4: Bring down the next term from the dividend.
-4x^2 + 0x + 25
Step 5: Divide the leading term of the new dividend by the leading term of the divisor.
-4x^2 / 2x = -2x
Step 6: Multiply the divisor by the quotient obtained in Step 5.
(-2x)(2x + 5) = -4x^2 - 10x
Step 7: Subtract the result obtained in Step 6 from the new dividend.
(-4x^2 + 0x + 25) - (-4x^2 - 10x) = 10x + 25
Step 8: Bring down the next term from the dividend.
10x + 25
Step 9: Divide the leading term of the new dividend by the leading term of the divisor.
10x / 2x = 5
Step 10: Multiply the divisor by the quotient obtained in Step 9.
(5)(2x + 5) = 10x + 25
Step 11: Subtract the result obtained in Step 10 from the new dividend.
(10x + 25) - (10x + 25) = 0
Step 12: Since the new dividend is zero, we stop the division.
Therefore, the quotient of (2x^3 + x^2 + 25) divided by (2x + 5) is x^2 - 2x + 5.
What is the sum of 3/12 + 2/12
Answers
Answer:
5/12
Step-by-step explanation:
b. in general, when dealing with inferences for two population proportions, which two of the following are equivalent: confidence interval method; p-value method; critical value method?
Answers
The confidence interval and critical value methods are equivalent in providing an interval estimate, the p-value method is used for hypothesis testing and evaluates the strength of evidence against the null hypothesis.
What is the confidence interval?
A confidence interval is a range of values that is likely to contain the true value of an unknown population parameter, such as the population mean or population proportion. It is based on a sample from the population and the level of confidence chosen by the researcher.
In general, when dealing with inferences for two population proportions, the confidence interval method and the critical value method are equivalent. These two methods provide a range of plausible values (confidence interval) for the difference between two population proportions and involve the calculation of critical values to determine the margin of error.
On the other hand, the p-value method is not equivalent to the confidence interval and critical value methods. The p-value method involves calculating the probability of observing a test statistic as extreme as, or more extreme than, the one obtained from the sample data, assuming the null hypothesis is true. It is used in hypothesis testing to determine the statistical significance of the difference between two population proportions.
To summarize:
- Confidence interval method: Provides a range of plausible values for the difference between two population proportions.
- Critical value method: Uses critical values to determine the margin of error in estimating the difference between two population proportions.
- P-value method: Determines the statistical significance of the observed difference between two population proportions based on the calculated p-value.
Hence, the confidence interval and critical value methods are equivalent in providing an interval estimate, the p-value method is used for hypothesis testing and evaluates the strength of evidence against the null hypothesis.
Learn more about the confidence interval here:
https://brainly.com/question/20309162
#SPJ4
Is the following relation a function?
Y = 3x
Answers
Answer:
Yes
Step-by-step explanation:
If you subsitute for x, x will only repeat if it has the same y value.
Yes, The given relation is a function.
Here,
The relation is given as; Y = 3x
We have to find the given relation is a function or not.
What is Function?
A relation is said to be function if there is exactly one value for each value of y.
Now,
The given relation is,
Y = 3x
When, we put x = 1 then y = 3
And, when x = 2 then y = 6 and so on.
Clearly, there is exactly one value of x for value of y.
So, The given relation is a function.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ2
1. Let the distribution of X be the normal distribution N (μ, σ2) and let Y = aX + b. Prove that Y is distributed as N (aμ + b, a2σ2).
2. Let X and Y be two independent random variables with E|X| < [infinity], E|Y| < [infinity] and E|XY| < [infinity]. Prove that E[XY] = E[X]E[Y].
Answers
1 Y is distributed as N(aμ + b, a^2σ^2), as desired.
2 We have shown that under these conditions, E[XY] = E[X]E[Y].
To prove that Y is distributed as N(aμ + b, a^2σ^2), we need to show that the mean and variance of Y match those of a normal distribution with parameters aμ + b and a^2σ^2, respectively.
First, let's find the mean of Y:
E(Y) = E(aX + b) = aE(X) + b = aμ + b
Next, let's find the variance of Y:
Var(Y) = Var(aX + b) = a^2Var(X) = a^2σ^2
Therefore, Y is distributed as N(aμ + b, a^2σ^2), as desired.
We can use the definition of covariance to prove that E[XY] = E[X]E[Y]. By the properties of expected value, we know that:
E[XY] = ∫∫ xy f(x,y) dxdy
where f(x,y) is the joint probability density function of X and Y.
Then, we can use the fact that X and Y are independent to simplify the expression:
E[XY] = ∫∫ xy f(x) f(y) dxdy
= ∫ x f(x) dx ∫ y f(y) dy
= E[X]E[Y]
where f(x) and f(y) are the marginal probability density functions of X and Y, respectively.
Therefore, we have shown that under these conditions, E[XY] = E[X]E[Y].
Learn more about distributed here:
https://brainly.com/question/29664127
#SPJ11
can yall help wit dis

Answers
What is the lateral area of the cone to the nearest whole number? The figure is not drawn to scale.
*
Captionless Image
34311 m^2
18918 m^2
15394 m^2
28742 m^2

Answers
Answer:
π(70)(√(70^2 + 50^2)) = π(700√74) m^3
= 18,918 m^3
Let U = {(x, y, z) € R^3 | x + 2y – 3z =0}. a) (2pt) Show directly (by verifying the conditions for a subspace) that U is a subspace of R^3. You may not invoke results learned in class or from the notes. b) (2pts) Find a basis for U. You must explain your method. c) (1pt) Using your answer from part b) determine Dim(U).
Answers
a) U is subspace of R^3.
b) The set {(3, -2, 0), (0, 1/2, 1)} is a basis for U.
c) 2.
a) To show that U is a subspace of R^3, we need to verify the following three conditions:
i) The zero vector (0, 0, 0) is in U.
ii) U is closed under addition.
iii) U is closed under scalar multiplication.
i) The zero vector is in U since 0 + 2(0) - 3(0) = 0.
ii) Let (x1, y1, z1) and (x2, y2, z2) be two vectors in U. Then we have:
x1 + 2y1 - 3z1 = 0 (by definition of U)
x2 + 2y2 - 3z2 = 0 (by definition of U)
Adding these two equations, we get:
(x1 + x2) + 2(y1 + y2) - 3(z1 + z2) = 0
which shows that the sum (x1 + x2, y1 + y2, z1 + z2) is also in U. Therefore, U is closed under addition.
iii) Let (x, y, z) be a vector in U, and let c be a scalar. Then we have:
x + 2y - 3z = 0 (by definition of U)
Multiplying both sides of this equation by c, we get:
cx + 2cy - 3cz = 0
which shows that the vector (cx, cy, cz) is also in U. Therefore, U is closed under scalar multiplication.
Since U satisfies all three conditions, it is a subspace of R^3.
b) To find a basis for U, we can start by setting z = t (where t is an arbitrary parameter), and then solving for x and y in terms of t. From the equation x + 2y - 3z = 0, we have:
x = 3z - 2y
y = (x - 3z)/2
Substituting z = t into these equations, we get:
x = 3t - 2y
y = (x - 3t)/2
Now, we can express any vector in U as a linear combination of two vectors of the form (3, -2, 0) and (0, 1/2, 1), since:
(x, y, z) = x(3, -2, 0) + y(0, 1/2, 1) = (3x, -2x + (1/2)y, y + z)
Therefore, the set {(3, -2, 0), (0, 1/2, 1)} is a basis for U.
c) Since the basis for U has two elements, the dimension of U is 2.
Learn more about subspace
brainly.com/question/30318872
#SPJ11
A newsletter publisher believes that above 32% of their readers own a personal computer. Is there sufficient evidence at the 0.05 level to substantiate the publisher's claim
Answers
There is insufficient evidence to substantiate the publisher's claim at the 0.05 level of significance.
How to determine if there is sufficient evidence to substantiate the publisher's claim?To determine if there is sufficient evidence to substantiate the publisher's claim, we need to conduct a hypothesis test.
Let's assume the null hypothesis is that the proportion of readers who own a personal computer is equal to 0.32.
The alternative hypothesis is that the proportion is greater than 0.32.
We can use a one-tailed z-test for proportions to test the hypothesis.
At the 0.05 level of significance, the critical z-value for a one-tailed test is 1.645.
If our calculated z-value is greater than 1.645, we reject the null hypothesis and conclude that there is sufficient evidence to support the publisher's claim.
Assuming we take a random sample of readers and find that 350 out of 1000 readers own a personal computer, the calculated z-value can be computed as:
\(z = (p - P) / \sqrt( P(1-P) / n )\)
where
p = sample proportion = 350/1000 = 0.35
P = hypothesized proportion = 0.32
n = sample size = 1000
z = (0.35 - 0.32) / sqrt( 0.32 * 0.68 / 1000 )
z = 1.42
Since the calculated z-value (1.42) is less than the critical z-value (1.645), we fail to reject the null hypothesis.
Therefore, there is insufficient evidence to substantiate the publisher's claim at the 0.05 level of significance.
Learn more about hypothesis testing
brainly.com/question/30588452
#SPJ11
i will mark brainliest!!!
Other answers: C. y=25x
D. y=25x+8.34

Answers
Answer:
Omg why are you soo beautiful? I love it
y = 8.34x + 25
Step-by-step explanation:
(10, 108.4) (20, 191.8)
m = slope
m = (y2 - y1)/(x2 - x1)
m = 191.8 - 108.4/20 - 10
m = 83.4/10
m = 8.34
She collects rainwater in a large barrel that weighs 25 pounds (y-intercept) so therefore, our answer should be y = 8.34x + 25
25 pts
Whats the degree of power function for this table

Answers
Answer:
x5
Step-by-step explanation:
Need help with this before I get cross.

Answers
Answer: Volume = 1330.6cm³
Step-by-step explanation:
The volume of a cylinder is expressed as:
"V= πr²h"
Base of the cylinder /diameter = 11cm
Hence radius = 11/2= 5.5cm
Length/height of cylinder = 14cm
Volume = 3.142*(5.5)²*14
3.142*30.25*14
1330.637cm³
1 decimal place is rounded to 1330.6cm³
Answer:
5321.9
Step-by-step explanation:
V= πr2h
so
π×11²×14= 5321.85796
5321.85796 rounder to 1 decimal place= 5321.9
Hope this helped you- have a good day bro cya)
talks about a row of triangular tables (5 triangular tables - in different directions to make a row)... how many children can sit around 1 table? a row of tables? around a row of 3 tables
Answers
The number of children that can sit around the entire row of 5 triangular tables is 15. When it comes to a row of 3 tables, a total of 9 children can sit around them.
Each triangular table has three sides, and each side can accommodate one child. Therefore, one triangular table can seat 3 children.
In a row of 5 triangular tables, since each table can seat 3 children, the total number of children that can sit around the entire row is 5 tables * 3 children per table = 15 children. Each table contributes 3 seats, and there are 5 tables in the row.
For a row of 3 tables, the same logic applies. Each table can accommodate 3 children, so the total number of children that can sit around the row of 3 tables is 3 tables * 3 children per table = 9 children.
Hence, whether it is a single table, a row of tables, or a row of 3 tables, each table can seat 3 children, resulting in a total number of seats equal to the number of tables multiplied by 3.
Learn more about triangular table here:
https://brainly.com/question/14573931
#SPJ11
A researcher wants to know the average number of times per month respondents eat at fast food restaurants. The statistic that s/he is most interested in would be the_________. A. standard deviation B. proportion C. mean D. variance
Answers
The statistic that the researcher would be most interested in for determining the average number of times per month respondents eat at fast food restaurants is the mean. The mean represents the average value of a set of data points and is commonly used to measure central tendency.
In this case, the researcher wants to know the average number of times per month respondents eat at fast food restaurants. By calculating the mean, the researcher can obtain a single value that represents the typical or average frequency of eating at fast food restaurants among the respondents. The standard deviation (A) is a measure of the dispersion or variability of the data points around the mean. The proportion (B) is a measure of the relative size or fraction of a subgroup within a larger group. The variance (D) is a measure of the average squared deviation from the mean. While these statistics can provide valuable information, they are not specifically suited to determine the average number of times per month respondents eat at fast food restaurants. Hence, the most relevant statistic in this scenario would be the mean (C).
Learn more about mean here:
https://brainly.com/question/12789483
#SPJ11
determine the surface area of a right circular cone that has a slant height of 5.8 ft and a diameter of 6.4 ft? round your answer to the nearest whole.

Answers
Answer:
it is 6.4*5.8 brainliest?
Step-by-step explanation:
During what ten-year period did the average age increase the most? a. from 1970 to 1980 b. from 1980 to 1990 c. from 1910 to 1920 d. from 1940 to 1950
Answers
During from 1980 to 1990 ten-year period did the average age increase the most
What is age ?Age is the duration of something's existence or being alive.
East Asian age calculation, a method of calculating age in Asia that begins at 1
Getting older, also referred to as aging,
Senescence, the age-related progressive decline in biological function
human advancement (biology)
Periodization, the division of history into clearly delineated chronological periods with names,
The stages of human existence on Earth as described by Greek mythology and its later Roman interpretation are known as the "Ages of Man."
Age before time
the given name age
Aage is the pen name of Italian screenwriter Agenore Incrocci.
To learn more about age from the given link:
https://brainly.com/question/927362
#SPJ4
9) If point B with coordinates (5, 2) is dilated by a scale factor of 3, what will be the coordinates of the image point B'?
Answers
Answer
Option A is correct.
B' (15, 6) is the answer.
Explanation
To dilate a given coordinate (x, y) about the origin by a scale factor of n, we will obtain (nx, ny).
So, for the given coordinate (5, 2), dilating by the scale factor of 3, we will obtain
B (5, 2) = B' (5×3, 2×3) = B' (15, 6)
Hope this Helps!!!
What are the roots of the polynomial equations
x^2+x-72=0
X^2-12x+20
0=x^2-4x-60
X^2+24=-11x
0=x^2-x-72
Answers
Answer:
A) x = -9, x = 8
B) x = 2, x = 10
C) x = -6, x = 10
D) x = -8, x = -3
E) x = -8, x = 9
Step-by-step explanation:
\(\boxed{\begin{aligned}&\textsf{Given}: \quad &x^2+x-72& =0\\&\textsf{Rewrite the term in $x$}: \quad &x^2+9x-8x-72& =0\\&\textsf{Factor the first two and last two terms}: \quad &x(x+9)-8(x+9)& =0\\&\textsf{Factor out $(x+9)$}: \quad &(x-8)(x+9)& =0\\&\textsf{Apply the zero-product property}: \quad &(x-8) &=0 \implies x=8\\&&(x+9)&=0 \implies x=-9\\&\textsf{Therefore, the roots are}: \quad & x&=-9,\;8\end{aligned}}\)
\(\boxed{\begin{aligned}&\textsf{Given}: \quad &x^2-12x+20&=0\\&\textsf{Rewrite the term in $x$}: \quad &x^2-10x-2x+20& =0\\&\textsf{Factor the first two and last two terms}: \quad &x(x-10)-2(x-10)& =0\\&\textsf{Factor out $(x-10)$}: \quad &(x-2)(x-10)& =0\\&\textsf{Apply the zero-product property}: \quad &(x-2) &=0 \implies x=2\\&&(x-10)&=0 \implies x=10\\&\textsf{Therefore, the roots are}: \quad & x&=2,\;10\end{aligned}}\)
\(\boxed{\begin{aligned}&\textsf{Given}: \quad &x^2-4x-60&=0\\&\textsf{Rewrite the term in $x$}: \quad &x^2-10x+6x-60& =0\\&\textsf{Factor the first two and last two terms}: \quad &x(x-10)+6(x-10)& =0\\&\textsf{Factor out $(x-10)$}: \quad &(x+6)(x-10)& =0\\&\textsf{Apply the zero-product property}: \quad &(x+6) &=0 \implies x=-6\\&&(x-10)&=0 \implies x=10\\&\textsf{Therefore, the roots are}: \quad & x&=-6,\;10\end{aligned}}\)
\(\boxed{\begin{aligned}&\textsf{Given}: \quad &x^2+24&=-11x\\&\textsf{Add $11x$ to both sides}: \quad &x^2+11x+24&=0\\&\textsf{Rewrite the term in $x$}: \quad &x^2+8x+3x+24& =0\\&\textsf{Factor the first two and last two terms}: \quad &x(x+8)+3(x+8)& =0\\&\textsf{Factor out $(x+8)$}: \quad &(x+3)(x+8)& =0\\&\textsf{Apply the zero-product property}: \quad &(x+3) &=0 \implies x=-3\\&&(x+8)&=0 \implies x=-8\\&\textsf{Therefore, the roots are}: \quad & x&=-8,\;-3\end{aligned}}\)
\(\boxed{\begin{aligned}&\textsf{Given}: \quad &x^2-x-72& =0\\&\textsf{Rewrite the term in $x$}: \quad &x^2-9x+8x-72& =0\\&\textsf{Factor the first two and last two terms}: \quad &x(x-9)+8(x-9)& =0\\&\textsf{Factor out $(x-9)$}: \quad &(x+8)(x-9)& =0\\&\textsf{Apply the zero-product property}: \quad &(x+8) &=0 \implies x=-8\\&&(x-9)&=0 \implies x=9\\&\textsf{Therefore, the roots are}: \quad & x&=-8,\;9\end{aligned}}\)
À television ser costs $350 cash. When
bought on hire purchase, a deposit of $35 is
required, followed by 12 monthly payments
of $30. How much is saved by paying cash
Answers
Answer:
$45.
Step-by-step explanation:
When the TV is bought on hire purchase, you deposit $35 and pay $30 monthly. There are 12 payments. 12 * 30 = $360. 360 + 35 = $395.
Since cash would've cost $350, the amount of money saved by paying cash is 395 - 350 = $45.
Hope this helps!
2 doctors is
% of 25 doctors.
Answers
The percentage of doctors that makes up 2 of 25 total number of doctors would be = 8%
How to calculate the percentage of doctors?The total number of doctors that are given = 25
The equivalent of 25 doctors in percent = 100%
Therefore the equivalent of 2 doctor in percentage= ?
That is;
100% = 25 doctors
X % = 2 doctors
Make X the subject of formula;
X = 100×2/25
X = 200/25
X= 8%
Learn more about percentage here:
https://brainly.com/question/24304697
#SPJ1
graph of f(x)= -3x*2+12and g(x)=mx+6
Answers
Answer:
see the picture
Step-by-step explanation:
hope it helps you
please follow me please


Please help the answer options are
1 mph
1 hour per mile
2mph
2 hours per mile

Answers
Answer:
I am positve it 2mph
Step-by-step explanation:
becuase for evry hr u drive 2 miles
the manager of a local stadium is interested in how many fans purchase peanuts at events. in a random sample of ,200 fans chosen from several different events, 94 of them purchased peanuts. what does this data imply about the claim that half of the people who attend events purchase peanuts?
Answers
According to the given data 47% of the fans that attend the event, purchase the peanuts.
The sample collected was among 200 fans which means total fans = 200
out of which 94 fans purchased peanuts which means
Percentage of Fans purchased Peanuts = \(\frac{94}{200}\) X 100
= 47 %
Not exactly the half of the fans purchased the peanuts but approximately half that is 3% less than 50 % fans puchased the peanuts which implies => 47 % fans purchased peanuts.
#SPJ4
please help!!! I need this and I also don't understand

Answers
Answer:
ABGE is a parallelogram because it has congruent sides
Step-by-step explanation:
:-)
the manager of a computer retails store is concerned that his suppliers have been giving him laptop computers with lower than average quality. his research shows that replacement times for the model laptop of concern are normally distributed with a mean of 3.7 years and a standard deviation of 0.6 years. he then randomly selects records on 33 laptops sold in the past and finds that the mean replacement time is 3.5 years.assuming that the laptop replacement times have a mean of 3.7 years and a standard deviation of 0.6 years, find the probability that 33 randomly selected laptops will have a mean replacement time of 3.5 years or less.
Answers
The probability of 33 randomly selected laptops having a mean replacement duration of 3.5 years or fewer is roughly 0.0287, or 2.87%.
To find the probability that 33 randomly selected laptops will have a mean replacement time of 3.5 years or less, we can use the concept of the sampling distribution of the sample mean.
Given that the population means replacement time is 3.7 years and the standard deviation is 0.6 years, and assuming that the distribution is approximately normal, we can use the formula for the standard error of the mean:
Standard Error (SE) = σ / √n
where n is the sample size and σ is the population standard deviation.
In this case, σ = 0.6 years and n = 33. Plugging these values into the formula, we get:
SE = 0.6 / √33 ≈ 0.1045
Next, we need to calculate the z-score for the sample mean of 3.5 years. The z-score formula is:
z = (x - μ) / SE
where x represents the sample mean, μ represents the population mean, and SE represents the standard error.
Plugging in the values, we have:
z = (3.5 - 3.7) / 0.1045 ≈ -1.91
Now, we can use a standard normal distribution table to find the probability associated with this z-score. The probability represents the area under the curve to the left of the z-score.
Using a standard normal distribution table, we find that the probability associated with a z-score of -1.91 is approximately 0.0287.
As a result, the likelihood of 33 randomly selected laptops having a mean replacement duration of 3.5 years or fewer is roughly 0.0287, or 2.87%.
Learn more about Standard Error:
https://brainly.com/question/30402690
#SPJ4
A plane that carries mail makes a round trip each day from Chicago to New York. It makes 2 intermediate stops on the way to New York and 3 intermediate stops on the way back to Chicago. Suppose you make a graph of the altitude of the plane for one day, with time on the horizontal axis and altitude on the vertical axis. How many times will the graph touch the horizontal axis?
A.8
B.13
C.5
D.7
Answers
Answer:
Step-by-step explanation:
7(d)
Evaluate. 0 0 O 8 0 -8 4eI need help with this question

Answers
PLZZ HELP FOR BRAINLIEST
What is the y-intercept of the graph?
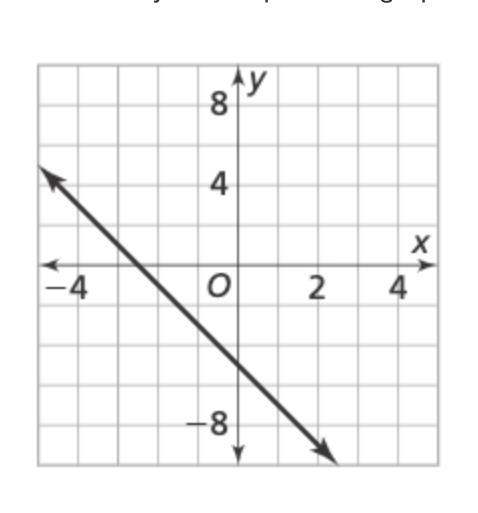
Answers
Answer:
-5
Step-by-step explanation: