Which relation below is NOT a function?
A. {(-2, 4), (1,3), (0,4)}
B. {(5,5), (4,4), (3,3) }
C. {(-4,0), (-7,0), (11, 0)}
D. {(1,4), (2,5) (1,7)}
Answers
D has two possible values of y when x = 1 therefore it is NOT a function
Related Questions
How would I start this?

Answers
Answer:
(0, ∞)
Step-by-step explanation:
A good place to start is by visualizing what the graph looks like on a number line.
For x > 0, it is an open circle at x=0, and shading to the right extending to infinity.
__
So, the left end of the interval is 0, but 0 is not included in the interval.
The right end of the interval is infinity, but there is no such number, so "infinity" is not included in the interval.
"Not included" means you use round brackets ( ) for the corresponding end of the interval. ("Included" would mean you use square brackets [ ].)
So, the interval 0 < x < ∞ is written in interval notation as ...
(0, ∞)
The graph represents a relation where x represents the independent variable and y represents the dependent variable.
A coordinate plane with points at negative 4 comma 4, negative 2 comma 0, 0 comma negative 3, 3 comma 1, and 5 comma negative 2.
What is the domain of the relation?
{−4, −3, −2, 0, 1, 3, 4, 5}
{−4, −2, 0, 3, 5}
{−3, −2, 0, 1, 4}
{0, 3, 4, 5}
Answers
The domain of the relation of the graph representing a relation where x represents the independent variable and y represents the dependent variable is {−4, −2, 0, 3, 5}.
How to determine domain relation?The domain of a relation is the set of all possible input values (independent variable) for which the relation is defined.
Looking at the given points, the x-coordinates are -4, -2, 0, 3, and 5. So, the possible input values are -4, -2, 0, 3, and 5.
Therefore, the domain of the relation is {−4, −2, 0, 3, 5}.
Hence, the correct option is {−4, −2, 0, 3, 5}.
Find out more on domain here: https://brainly.com/question/26098895
#SPJ1
BRAINLIEST TO CORRECT

Answers
Answer:
2 4/9
Step-by-step explanation:
Get common denominators:
1/3= 3/9
Then subtract:
7/9-3/9=4/9
8-6=2
Then add:
2+4/9= 2 4/9
Hope this helps! :)
Pls mark brainliest if correct:)
What’s the correct answer answer asap for brainlist

Answers
Answer:
your answer is B
Step-by-step explanation:
Germany, Austria-Hungary, Bulgaria, and the Ottoman Empire
How large must a group of people be in order to guarentee that there are at least two people in the group whose birthdays fall in the same month
Answers
Answer:
13
Step-by-step explanation:
This problem is an example of pigeonhole principle which states that If n+ 1 objects are placed into n boxes, then some box contains at least 2 objects.
Here no. of months in a year are boxes n = 12.
Therefore number of objects( people) = n+1= 13.
Then,at least two people in the group whose birthdays fall in the same month.
Tanner is 2 years younger than his brother. Tanners age t in years is 2 years less than his brothers age b
Answers
Answer:is his brother 4 or 8
Step-by-step explanation:
I don't know for sure
The relationship between Tanner's age and his brother's age can be represented by the equation:
t = b - 2
This equation states that Tanner's age (t) is equal to his brother's age (b) minus 2 years.
help me solve this queston

Answers
TJohn's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
To represent the given problem as a system of equations, we can use the following information:
John is 70 years younger than Sharon: j = s - 70
Sharon is 4 times as old as John: s = 4j
Let's plot the graph for this system of equations:
First, let's solve equation (2) for s:
s = 4j
Now substitute this value of s in equation (1):
j = s - 70
j = 4j - 70
3j = 70
j = 70/3
Substitute the value of j back into equation (2) to find s:
s = 4j
s = 4(70/3)
s = 280/3
The solution to the system of equations is j = 70/3 and s = 280/3
In the graph d, the solution to the system of equations is represented by the point (70/3, 280/3), which is approximately (23.33, 93.33) on the graph.
Therefore, John's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
Learn more about system of equations click;
https://brainly.com/question/20067450
#SPJ1

Solve for X.
The solution is X _ _

Answers
Step-by-step explanation:
x is lesser or equal to negative 6

Factor the expression
(x+2)^2-25y^4
Answers
Answer:
(x+2-5y^2) (x+2+5y^2)
Step-by-step explanation:
......,....................
This is the right answer.
PLease help, this is due tomorrow by 1 pm.

Answers
Note that the parameters of the graph a and graph b are given below.
Graph A - y=2(x-1)²
See graph attached.
Graph B - y = 1/2x² + 3
Vertex: The vertex of the function is (0, 3).
Axis of symmetry: The axis of symmetry is the vertical line passing through the vertex, which is x = 0.
Y-intercept: The y-intercept is the point where the graph intersects the y-axis. It is (0, 3).
Minimum or maximum: The coefficient of x² is positive, which means the parabola opens upwards, and therefore the function has a minimum value. The minimum value is 3.
Solutions: To find the solutions or roots of the quadratic equation, we need to set y or f(x) equal to zero and solve for x.
0 = 1/2 x² + 3
Subtracting 3 from both sides, we get:
-3 = 1/2 x²
Multiplying both sides by -2, we get:
6 = -x²
Taking the square root of both sides, we get:
x = ±√(-6)
Since the square root of a negative number is not a real number, the function has no real roots.
Minimum or maximum value: The minimum value of the function is 3.
Range: The range of the function is y ≥ 3, because the function has a minimum value of 3.
Domain: The domain of the function is all real numbers, because there are no restrictions on the values of x for which the function is defined.
Stretch/Shrink/Standard: The coefficient of x^2 is positive and less than 1, which means that the graph of the function is narrower than the graph of y = x². This is an example of a standard quadratic function that has been vertically compressed by a factor of 1/2.
See graph attached.
Learn more about graphs at:
https://brainly.com/question/17267403
#SPJ1


One end of a wire is attached to the top of a 24-foot pole; the other end of the wire is anchored to the ground
18 feet from the bottom of the pole. If the pole makes an angle of 90° with the ground, find the length of the
wire.
Answers
Answer:
30 feet
Step-by-step explanation:
We can use Pythagorean theorem for this question because the pole and the wire that is anchored to the ground forms an right triangle because the pole makes an angle of 90 degrees.
One side of the right triangle formed is equal to 24 feet, and because the wire that is anchored to the ground is 18 feet from the bottom of the pole, another side is 18 feet.
Pythagorean theorem states that \(a^{2} +b^{2} =c^{2}\). With a and b being the sides of the right triangle and c being the hypotenuse. In this problem, the length of the wire is equal to the hypotenuse of the triangle.
a=24 and b =18. 24 squared is equal to 576, and 18 squared is equal to 324. We add 576 and 324, which is 900. This means that \(c^{2}\) =900. To find c, we find the square root of 900, which is 30. Therefore, the length of the wire is 30 feet.
Answer:
30 feet
Step-by-step explanation:
1. The 24-foot pole and the 18 feet from the bottom of the pole form a right angle, meaning that when you add the length of the wire, a right triangle forms.
2. "24-foot pole" is the height, and "18 feet from the bottom of the pole" is the base. The length of the wire is the hypotenuse.
3. To find the hypotenuse of a right triangle, we can use the Pythagorean theorem to solve it: \(a^2 + b^2 = c^2\), where a = leg of triangle, b = leg of triangle, and c = hypotenuse (or in this case, the wire).
4. Now, let's apply the formula:
\(18^2 + 24^2 = c^2\)Step 1: Simplify both sides of the equation.
\((18*18)+(24*24)=c^2\) \(324 + 576 = c^2\) \(900 = c^2\)Step 2: Take square root of both sides.
\(\sqrt{900} =\sqrt{c^2}\) \(30 = c\)Step 4: Check if solution is correct.
\((18*18)+(24*24)=(30*30)\) \(324 + 576 = 900\) \(900 = 900\)Therefore, the length of the wire is 30 feet.
What is the common ratio of the geometric sequence below?
625, 125, 25, 5, 1,
Answers
The common ratio is 1/5. By dividing each word by the term before it, we may find the geometric progression's common difference.
How to find common ratio ?The common ratio in geometric progression is the ratio of any term in the sequence to divided by the first term.
The Formula to calculate the common ratio in geometric progression, a, ar, ar2, ar3, ar4, ar5… is,
Common ratio = ar/ a = ar2/ ar = ……. = an/ an-1
As stated in the definition, we can compute the common difference of a geometric progression by dividing any term by its preceding term.
Given, the geometric sequence is 625, 125, 25, 5, 1,....
We have to find the common ratio of the given geometric sequence.
In geometric sequence, a, b, c, d, … the common ratio r is given by
r = b/a = c/b = d/c.
So, r = 125/625 = 25/125 = 5/25 = 1/5;
r = 1/5
Therefore, the common ratio is r = 1/5.
To learn more about common ratio refer :
https://brainly.com/question/26509106
#SPJ1
Answer:
B. 25/125
Step-by-step explanation:
Please answer 2-5Drag a statement or reason to each box to complete this proof. If−2(x+1)=8, thenx=−5

Answers
The given equation is
\(-2(x+1)=8\)2. Division Property of Equality.
3. x+1=-4
4. Subtraction Property of Equality.
5. x=-5
Find the LCM of 6,12 and 15
Answers
LCM=2×2×3×5=2×6×5=2×30=60

Step-by-step explanation:
\(\large \boldsymbol{} \sf 6=\bold3\cdot \underline2 \\\\12=\bold3\cdot \underline2\cdot 2\\\\15=5\cdot\bold 3 \\\\ LCM(6 ; 12 ; 15) =\bold{3\cdot 2}\cdot 2\cdot 5=60\)
Number of points scored in each basketball game: 28,16,38,44,21,38,35,48,33,29,37,39,18,38,42,37,32
Answers
Answer:
unm okay? is there anything more to the question?
I need help with this PLEASE!!!

Answers
Answer:
See the image for marked congruences.
1. JM ≅ LM | Given
2. △JML is isosceles | definition of isosceles
3. ∠MJL ≅ ∠MLJ | isosceles triangle theorem
4. m∠MJL = m∠MLJ | definition of ≅
5. JK ≅ LK | Given
6. △JKL is isosceles | definition of isosceles
7. m∠KJL = m∠KLJ | isosceles triangle theorem
8. m∠MJL + m∠KJM = m∠KJL | adjacent angle theorem
9. m∠MLJ + m∠KMJ = m∠KLJ | adjacent angle theorem
10. m∠MJL + m∠KJM = m∠MLJ + m∠KLM | transitive property of =
11. m∠MJL + m∠KJM = m∠MJL + m∠KLM | substitution
12. m∠KJM = m∠KMJ | subtraction
13. ∠KJM ≅ ∠KLM | definition of ≅
14. △KJM ≅ △KLM | SAS theorem
15. ∠JKM ≅ ∠LKM | CPCTC
16. KM bisects ∠JKL | definition of bisector

g Four distinct numbers are to be selected from the list {−5, −4, −3, −2, −1, 1, 2, 3, 4}. In how many ways can this selection be done so that the product of the four numbers is positive?
Answers
Answer: 66 possible combinations.
Step-by-step explanation:
To have a positive product we have 3 situations.
The 4 numbers are positive:
if the "order" of the selection does not matter, then we have only one solution here:
1, 2, 3 and 4.
Second case, we have two negative numbers and two positive numbers.
Here we can use the fact that in a group of N objects, the number of different combinations of K objects (where K ≤ N) is:
\(C = \frac{N!}{(N -K)!*K!}\)
Here we have 5 negative numbers and we want to make groups of 2, so the possible combinations are:
\(C = \frac{5!}{3!*2!} = \frac{5*4}{2*1} = 2*5 = 10\)
And we have exactly the same for the other two positive numbers, but in this case we have N = 4 and K = 2.
\(C = \frac{4!}{2!*2!} = 6\)
The total number of combinations is the product of those two:
C = 10*6 = 60 combinations
Now, the last option is that the 4 numbers are negative numbers, so here we have 5 negative numbers and we want to make groups of 4.
\(C = \frac{5!}{1!*4!} = 5\)
So in total, we have: 1 + 60 + 6 = 66 possible combinations.
Please help me thank you

Answers
substitute the value in x ...
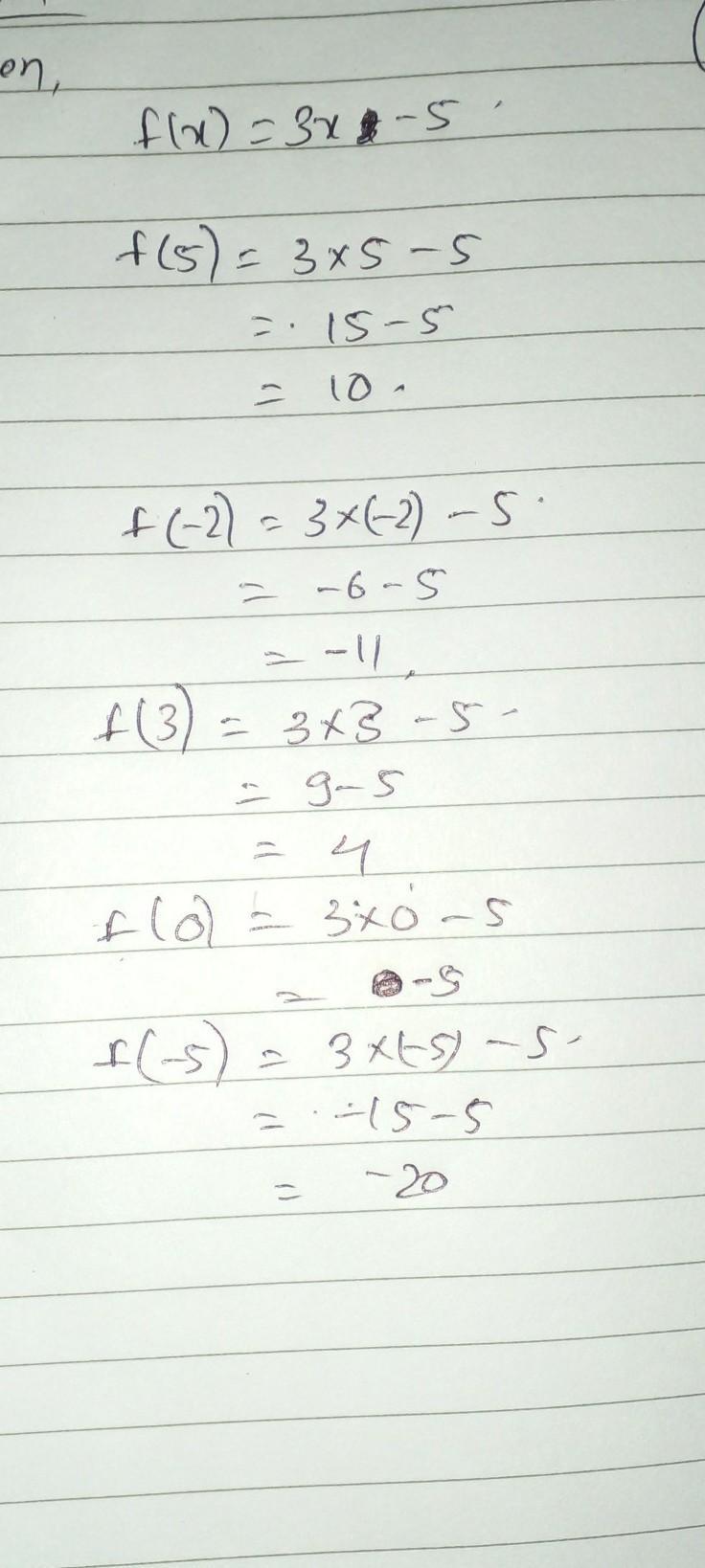
Where does the normal line to the paraboloid z = x2 + y2 at the point (1, 1, 2) intersect the paraboloid a second time?
Answers
Answer:
the intersection point is ( -5/4, -5/4, -9/8)
Step-by-step explanation:
F(x,y,z) = x² +y² -z= 0
Then find differential of each terms then we have
∀f(x)=2x
∀f(y)=2y
∀f(z)=-1
The partial differential which is the director vector is at F(x,y,z)= (1,1,2)
Vf(1,1,2) = (2,2,-1)
But the given point is ( 1.1,2)
Then the parametric equation of normal line will be
x= 1+2t
y= 1+2t
z= 2 -t
The parametric equation can be formed as
(1+2t)² + (1+2t)² - (2-t)= 0
If we expand the expression above we have,
2(1+4t+4t²) - 2+t= 0
0= 8t² + 9t
t= 0 or t= -9/8
Substitute the value of t into the parametric equation above
At t=0
x= 1+2t; x= 1+2(0)=1
y= 1+2t; y= 1+2(0)=1
z=2 -t ; z= 2-(0)= 2
At =0 , we have (1,1,2)
At t= -9/8
x= 1+2t; x= 1+2(-9/8)=-5/4
y= 1+2t; y= 1+2(-9/8)=-5/4
z=2 -t ; z= 2-(-9/8)= -9/8
Therefore, the intersection point is ( -5/4, -5/4, -9/8)
The normal intersects the paraboloid at \((-\frac{5}{4},-\frac{5}{4},\frac{25}{8} )\)
Paraboloid:A surface all of whose intersections by planes are either parabolas and ellipses or parabolas and hyperbolas.
Given function is,
\(z = x^2 + y^2\)
We can write the given function as,
\(F(x,y,z)=x^2+y^2-z\)
Compute the gradient \(F\) by using the formula,
\(\nabla F(x,y,z)=\left\langle 2x,2y,-1\right\rangle\)
At (1,1,2) we get,
\(\nabla F(x,y,z)=\left\langle 2,2,-1\right\rangle\)
The equation of the tangent plane at (1,1,2) is,
\(2(x-1)+2(y-1)-(z-2)=0\\2x+2y-z-2=0\\\frac{x-1}{2}=\frac{y-1}{2}=\frac{z-2}{-1}=t\\ x=2t+1,y=2t+1,z=-t+2\)
Replace the values of \(x,y,z\) in \(z = x^2 + y^2\) and then solve for \(t\) then,
\(-t+2=(2t+1)^2+(2t+1)^2\\8t^2+9t=0\\t=0,-\frac{9}{8}\)
Substituting the value into the parametric equations,
\(x=2(-\frac{9}{8} )+1,y=2(-\frac{9}{8} )+1,\ and \ z=-(-\frac{9}{8} )+2\\x=-\frac{5}{4}, \ y= -\frac{5}{4} ,z=\frac{25}{8}\)
Therefore, the normal intersects the paraboloid at \((-\frac{5}{4},-\frac{5}{4},\frac{25}{8} )\)
Learn more about the topics paraboloid:
https://brainly.com/question/17593461
The table represents a linear relationship
X—2 0 4
Y-4 3 1
Which equation represents the table
Y=1/2x+5
y=-1/2x+3
Y=2x-3
Y=-4x+2
Answers
The linear relationship illustrated in the provided table can be effectively described by the equation Y = -4x + 2. Option D.
To determine the equation that represents the given table with the values of x and y, we can observe the pattern and find the equation of the line that fits these points.
Given the table:
X: 2 0 4
Y: -4 3 1
We can plot these points on a graph and see that they form a straight line.
Plotting the points (2, -4), (0, 3), and (4, 1), we can see that they lie on a line that has a negative slope.
Based on the given options, we can now evaluate each equation to see which one represents the line:
Y = 1/2x + 5
When we substitute the x-values from the table into this equation, we get the following corresponding y-values: -3, 5, and 6. These values do not match the given table, so this equation does not represent the table.
Y = -1/2x + 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: 4, 3, and 2. These values also do not match the given table, so this equation does not represent the table.
Y = 2x - 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -4, -3, and 5. These values do not match the given table, so this equation does not represent the table.
Y = -4x + 2
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -6, 2, and -14. Interestingly, these values match the y-values in the given table. Therefore, the equation Y = -4x + 2 represents the table.
In conclusion, the equation Y = -4x + 2 represents the linear relationship described by the given table. So Option D is correct.
For more question on equation visit:
https://brainly.com/question/29174899
#SPJ8
y less than two thirds times x plus 2 (0, 3) (−3, 1) (3, 5) (1, 2)
Answers
As per the given statement, the inequality will be equal to y<2/3x+2.
What is an inequality?Inequalities are mathematical expressions where neither side is equal. In inequality, as opposed to equations, we compare the two values. Less than (or less than and equal to), larger than (or greater or equal to), or not similar to signs are used in place of the equal sign in between.
here, we have,
As per the data provided in the question,
The statement is,
y is less than 2/3 times of x, that is = y<(2/3)x and,
then it is plus two is added to the equation,
y<(2/3)x+2
To know more about inequality:
brainly.com/question/28823603
#SPJ1
(5 + 16) = 7 + (4 x 7) =
Bidmass
Answers
Answer:
(5 + 16)=7 + (4 x 7)
Step by step - explanation:
Solve:
Add the numbers
(5 + 16)= 21.
(4 x 7) = 28 + 7 = 35.
So the result is 21 = 35.
Hope that helps. x
Answer:
Step-by-step explanation:
(5+16)=7+(4.7)
(21)=7+(4.7)
21=7+(4.7)
21=7+(28)
21=7+28
21=35
Answer: 21=35
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the curves x=√y, x=0, and y=4 about the x-axis.
Answers
The volume generated by rotating the region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) about the x-axis using the method of cylindrical shells is \($4\pi$\) cubic units.
What is the formula for the volume of the cylinder?The formula for the volume of a cylinder is V = πr²h, where V is the volume, r is the radius, and h is the height.
According to given information :To find the volume generated by rotating the region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) about the x-axis using the method of cylindrical shells, we need to follow these steps:
Sketch the region and the axis of rotation. The region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) is a quarter-circle with radius 2 centered at the origin. The axis of rotation is the x-axis.
Choose a vertical strip with width $\Delta x$ that runs parallel to the y-axis and intersects the region. The height of this strip is given by the equation $y = 4 - x^2$.
Imagine rotating this strip around the x-axis to form a cylindrical shell with thickness \($\Delta x$\), height \($4 - x^2$\), and radius \($x$\).
The volume of this cylindrical shell is given by the formula \($V = 2\pi x(4-x^2)\Delta x$\).
To find the total volume of the solid, we need to add up the volumes of all the cylindrical shells. This can be done by taking the limit as the width of the strips $\Delta x$ approaches zero and summing up the volumes of the resulting shells. This gives us the integral:
\($V = \int_{0}^{2} 2\pi x(4-x^2) dx$\)
We can simplify this integral by expanding the expression inside the parentheses, which gives us:
\($V = \int_{0}^{2} 8\pi x - 2\pi x^3 dx$\)
We can then integrate each term separately to get:
\($V = [4\pi x^2 - \frac{1}{2}\pi x^4]_{0}^{2}$\)
\($V = (4\pi \cdot 2^2 - \frac{1}{2}\pi \cdot 2^4) - (4\pi \cdot 0^2 - \frac{1}{2}\pi \cdot 0^4)$\)
\($V = 8\pi - 4\pi = 4\pi$\)
Therefore, the volume generated by rotating the region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) about the x-axis using the method of cylindrical shells is \($4\pi$\) cubic units.
To learn more about the volume of the cylinder visit:
brainly.com/question/6204273
#SPJ1
Graph the arithmetic sequence.
$4,\ 12,\ 20,\ 28,\ ...$
Keyboard Instructions
Initial graph state
The horizontal axis goes from -0.8 to 6 with ticks spaced every 1 unit(s).
The vertical axis goes from -2 to 30 with ticks spaced every 4 unit(s).
Answers
The graph of the arithmetic sequence is added as an attachment
How to graph the arithmetic sequence?From the question, we have the following parameters that can be used in our computation:
Sequence: 4, 12, 20, 28....
The above sequence is an arithmetic sequence with the following parameters
First term, a = 4
Common difference, d = 8
So, the x-th term is
f(x) = a + (x - 1) * d
Substitute the known values in the above equation, so, we have the following representation
f(x) = 4 + (x - 1) * 8
This gives
f(x) = 8x - 4
So, the equation to plot is f(x) = 8x - 4
See attachment for the graph
Read more about sequence at
https://brainly.com/question/6561461
#SPJ1

50 Pts!!! Please answer without links or I won't give you brainliest!
Completely solve how to get the graph of this equation without using a calculator.
|x + 7| - 2
Answers
Select all the correct answers.
Consider the circle represented by this equation.
X^2+4x+y^2-2y-4=0
Which features are features of the circle?
center at (-2, 1)
radius of 1
radius of 3
radius of 9
center at (2,-1)
center at (-4, 2)
Answer ASPA
Answers
Based on the calculations, the features which are features of the circle include the following:
center at (-2, 1).radius of 9.What is a circle?A circle can be defined as a closed, two-dimensional curved geometric shape with no edges or corners. Also, a circle refers to the set of all points in a plane that are located at a fixed distance (radius) from a fixed point (central axis).
The equation of a circle.Mathematically, the standard form of the equation of a circle is given by;
(x - h)² + (y - k)² = r²
Where:
h and k represents the coordinates at the center.r represents the radius of a circle.Given the following equation:
x² + 4x + y² - 2y - 4 = 0
x² + 4x + y² - 2y = 4
Next, we would evaluate the equation by using completing the square method:
x² + 4x + 4 + y² - 2y + 1 = 4 + 5
(x² + 2x + 2x + 4) + (y² - y - y + 1) = 9
(x + 2)² + (y - 1)² = 3²
By comparing the above equation with the standard form of the equation of a circle, we have:
Center, h = -2.Center, k = 1.Radius, r = 3.Read more on equation of a circle here: https://brainly.com/question/24810873
#SPJ1
5 Some friends made a 12-piece quilt for the State Fair in Dallas. Inez sewed 2 4 of the quilt. Billy sewed 12 of the quilt, and Cass sewed 2 pieces. Who sewed the most pieces? A. Cass B. C. D. Billy Inez Inez and Billy, equally
Answers
Inez and Billy sewed the most pieces equally which is 6 pieces each.
What is an equation?An equation is an expression that shows how numbers and variables are related using mathematical operations. Equations can be linear, quadratic, cubic and so on.
Some friends made a 12-piece quilt for the State Fair in Dallas. Inez sewed 2/4 of the quilt. Billy sewed 1/2 of the quilt, and Cass sewed 2 pieces.
Hence:
Number of quilt sewed by Inez = (2/4) * 12 piece = 6 pieces
Number of quilt sewed by Billy = (1/2) * 12 piece = 6 pieces
Number of pieces sewed by Cass = 2 pieces
Inez and Billy sewed the most pieces.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
The population of a city decreases by 2.5% per year. If this year's population is 237,000, what will next year's population be, to the nearest individual?
Answers
Ejemplo: catalina compro una piscina para
ponerla en el jardín de su casa.
-Piscina cilíndrica 206cm de diámetro y 60cm
de profundidad además construirá una zona de
cemento y cerco de seguridad alrededor de la
piscina.
¿Cuál es el volumen máximo de agua que
puede contener la piscina? (considere T=3)
¿cuál es la extensión del cerco de seguridad?
(considere П=3)
Answers
The length of the fence must be 618cm
The volume that it can hold is 1,909,620 cm³
How to find the volume and the length of the fence?First, the fence is just equal to the circumference of the cylinder, remember that the circumfernce of a circle of diameter D is:
C = П*D
Here we use П = 3, then:
C = П*206cm
C = 3*206cm = 618cm
Now the volume, for a cylinder of diameter D and height H, the volume is:
V = П*(D/2)²*H
Replacing the values that we know we will get:
V = 3*(206cm/2)²*60cm = 1,909,620 cm³
Learn more about cylinders at:
https://brainly.com/question/9554871
#SPJ1
243, 81, 27, 9, 3, 1
Which of the following is the next term in the geometric sequence show above?
A. \\\ -3
B. \\\\ -1
C. \ -1/3
D. \\\\\\\ 0
E. \\\\\\ 1/3
Answers
Answer:
E. 1/3
Step-by-step explanation:
In this sequence, the numbers are descending and are 1/3 of the previous number.
243 / 3 = 81
81 / 3 = 27
9 / 3 = 3
3 / 3 = 1
1 / 3 = 1 / 3 (the next term)