Which property of equality is used to solve m+18= -9
Answers
Answer:
m=-27
Step-by-step explanation:

Related Questions
Use zero through third-order taylor series expansion to predict f(3) for
f(x)= 25x^3-6x^2+7x-88
Using a base point at x=1. compute the true percent relative error epsilon for each approximation.
Answers
The predicted value of f(3) is 108 using the third-order Taylor series expansion, and the true percent relative error for each approximation is ε₀ = 134.83%, ε₁ = 32.02%, ε₂ = 40.45%, and ε₃ = 39.33%.
The Taylor series expansion of the given function f(x) = 25x³ - 6x² + 7x - 88 about a base point x = 1 is given by:
Taylor series expansion for a function is given as:
f(x) = f(a) + f'(a)(x - a) + (f''(a)/2!)(x - a)² + (f'''(a)/3!)(x - a)³ + ... + Rn(a)
Where, a = 1, f(a) = 25(1)³ - 6(1)² + 7(1) - 88 = -62.
The first three derivatives of the function are:
f'(x) = 75x² - 12x + 7
f''(x) = 150x - 12f'''(x) = 150
The zeroth-order approximation is the same as f(1), i.e., -62.
The first-order approximation is given by:
f₁(x) = f(a) + f'(a)(x - a)f₁(3) = -62 + [75(1)² - 12(1) + 7](3 - 1) = 121
The second-order approximation is given by:
f₂(x) = f(a) + f'(a)(x - a) + (f''(a)/2!)(x - a)²
f₂(3) = -62 + [75(1)² - 12(1) + 7](3 - 1) + [150(1) / 2!](3 - 1)² = 106
The third-order approximation is given by:
f₃(x) = f(a) + f'(a)(x - a) + (f''(a)/2!)(x - a)² + (f'''(a)/3!)(x - a)³
f₃(3) = -62 + [75(1)² - 12(1) + 7](3 - 1) + [150(1) / 2!](3 - 1)² + [150 / 3!](3 - 1)³= 108
The true value of the function f(3) = 25(3)³ - 6(3)² + 7(3) - 88 = 178
The true percent relative error, ε is given by:
ε = |(Approximate value - True value) / True value| × 100
For zeroth-order approximation, ε₀ = |(-62 - 178) / 178| × 100 = 134.83%
For first-order approximation, ε₁ = |(121 - 178) / 178| × 100 = 32.02%
For second-order approximation, ε₂ = |(106 - 178) / 178| × 100 = 40.45%
For third-order approximation, ε₃ = |(108 - 178) / 178| × 100 = 39.33%
Hence, the predicted value of f(3) is 108 using the third-order Taylor series expansion, and the true percent relative error for each approximation is ε₀ = 134.83%, ε₁ = 32.02%, ε₂ = 40.45%, and ε₃ = 39.33%.
learn more about Taylor series expansion here:
https://brainly.com/question/32622109
#SPJ11
Find the value of x. Show your work, please!

Answers
The value of x is 10.
Given triangle is a right-angled triangle.
Let the lengths of not mentioned lengths be 2p(hypotenuse) and 2q (other side).
There are two triangles in the given picture.
Consider the smaller triangle.
Apply Pythagoras theorem to that i.e.,
\(p^{2}\) = \((3x)^{2} + q^{2}\)
(Here, total hypotenuse is 2p length and the smaller triangle has half of its length. So, length is p. Similarly in case of q)
\(p^{2} = 9x^{2} + q^{2}\) (Equation 1)
Now, consider the large triangle.
Apply Pythagoras theorem to that i.e.,
\((2p)^{2} = (4x + 20)^{2} + (2q)^{2}\)
\(4p^{2} = (16x^{2} + 160x + 400) + 4q^{2}\)
Substitute \(p^{2}\) from Equation 1
\(4(9x^{2} + q^{2} ) = 16x^{2} + 160x + 400 + 4q^{2}\\\)
\(36x^{2} + 4q^{2} = 16x^{2} + 160x + 400 + 4q^{2}\)
\(36x^{2} = 16x^{2} + 160x + 400\) (\(4q^{2}\) from both sides got cancelled)
\(20x^{2} - 160x - 400 = 0\)
Solving the quadratic equation,
\(20x^{2} - 200x + 40x - 400 = 0\)
\(20x(x - 10) + 40(x - 10) = 0\)
\((20x+ 40)(x - 10) = 0\)
So, 20x + 40 = 0 or x - 10 = 0
i.e., x = -2 or 1o
But \(x \neq -2\) because angles cannot be negative.
So, x is 10.
Learn more about right-angled triangles at -
brainly.com/question/21691679
A rectangular prism has whole number dimensions It has a height of 24 inches, a square base, and a surface area of 306 inches squared. What are the dimensions of the base of the prism?
Answers
Therefore, the prism's base can be either 9 x 9 inches, 6 x 6 inches, or
4 x 4 inches in size.
.
The Surface area is what?The amount of space that an object's surface takes up in total is measured by its surface area. It is usually expressed in square units, such as square inches or square metres.The surface area of a three-dimensional object can be determined by adding up the areas of all of its faces.
For instance, the surface area of a rectangular prism can be calculated using the formula below:
A = lw + lh + lw
The formula SA = 2lw + 2lh + 2wh, where l is the prism's length, w is its width, and h is its height, determines the surface area of a rectangular prism. Inputting the values provided yields:
306 is equal to 2l + 2(24) + 2(24) + 48
306 - 48l = 2w(l+24) 153 - 24
l = wl + 48w 153 - 48w = l(w+24) 153 - 24l - 48w = wl
We can identify all potential values of l and w that meet this equation because they are both whole numbers. Since it is a rectangular prism with a square base, we know that l > w. Given that the surface area cannot be more than 306, we also know that l(w+24) 153. We may therefore begin by identifying all variables of (153-48w) bigger than w.and equal to or less than 12 (since w cannot be greater than 12). We get:
W=1, L=9, L=2, L=6, and L=3
Therefore, the prism's base can be either 9 x 9 inches, 6 x 6 inches, or 4 x 4 inches in size.
To know more about surface area visit:
brainly.com/question/29298005
#SPJ1
150 is 75% of what number?
Answers
Answer:
200
Step-by-step explanation:
0.75X = 150
X = 200
so 200 is the answer
Answer:
200
150 is 75% of 200
Step-by-step explanation:
150 is 75% of what number
we can change this so it is simpler to understand.
150 = 75% of x
whenever it says "of" it is telling you to multiply
150 = 75% * x
now we simplify
150 = 75/100 * x
150 = 75x/100
*100 *100
15000 = 75x
/75 /75
200 = x
150 is 75% of 200
the function g(x) represents f(x)=9 cos (x-pi/2)+3 after translating pi/6 units left and 4 units up. which equation represents g(x)?
g(x)= 9 cos (x - 2pi/ 3) -1
g(x)= 9 cos (x - 2pi/3) +7
g(x)= 9 cos (x - pi/3) +7
g(x)= 9 cos (x - pi/3) -1
Answers
Answer:
g(x)= 9 cos (x - \(\frac{\pi}{3}\)) +7
Step-by-step explanation:
What is given is f(x) = g cos (x - pi/2) + 3
Note that the standard form of cosine function is a cos (bx + c) + d
a= amplitude
-c/b = phase shift
d = vertical shift
After moving pi/6 to the left --
x = pi/2 - pi/6 = pi/3
once moving pi/6 left, it is at pi/3
moving 4 units up just means adding 4 + 3, and that equals 7, that would be the vertical shift once applied.
So the equation that represents g(x) is C. 9 cos (x - pi/3) + 7
The equation that represents the function g(x) is \(g(x)=9 \cos (x- \frac{\pi}{3})+7\)
The function is given as:
\(f(x)=9 \cos (x-\frac{\pi}{2})+3\)
The function f(x) is first translated \(\frac{\pi}{6}\) units left.
The rule of this translation is:
\((x,y) \to (x + \frac{\pi}{6},y)\)
So, we have:
\(f'(x)=9 \cos (x+ \frac{\pi}{6}-\frac{\pi}{2})+3\)
Take LCM
\(f'(x)=9 \cos (x+ \frac{\pi - 3\pi}{6})+3\)
\(f'(x)=9 \cos (x- \frac{2\pi}{6})+3\)
Divide 2 by 6
\(f'(x)=9 \cos (x- \frac{\pi}{3})+3\)
Next, we translate f'(x) 4 units up.
The rule of this translation is:
\((x,y) \to (x,y+4)\)
So, we have:
\(g(x)=9 \cos (x- \frac{\pi}{3})+3 +4\)
\(g(x)=9 \cos (x- \frac{\pi}{3})+7\)
Hence, the equation that represents the function g(x) is \(g(x)=9 \cos (x- \frac{\pi}{3})+7\)
Read more about function transformation at:
https://brainly.com/question/1548871
Find the value of the variable in each expression

Answers
Answer:
they're all 0
Step-by-step explanation:
N/A
Please help me my teacher hasn't been helping me I really need your help

Answers
Answer:
550.5323531336038
Step-by-step explanation:
I have a hint: if you ever need help with triangle trigonometry questions go to carbside depot trigonometry calculator it is a literal life savor
A project is graded on a scale of 1 to 5. If the random variable, X, is the project grade, what is the mean of the probability distribution below? A probability distribution is shown. The probability of 1 is 0. 1; 2 is 0. 2; 3 is 0. 4; 4 is 0. 2; 5 is 0. 1. 0. 2 0. 4 1 2003.
Answers
Probability of an event is the measure of its chance of occurrence. The mean of the given probability distribution is 3
How to calculate the expectation(also called mean) of a discrete random variable?Expectation can be taken as a weighted mean, weights being the probability of occurrence of that specific observation.
Thus, if the random variable is X, and its probability mass function is given as: f(x) = P(X = x), then we have:
\(E(X) = \sum_{i=1}^n( f(x_i) \times x_i)\)
(n is number of values X takes)
For the given case, we have:
X = project grade (from 1 to 5, thus, 1, 2,3,4, or 5 as its values.)
The probability distribution of X is given as:
\(\begin{array}{cc}x&P(X = X)\\1&0.1\\2&0.2\\3&0.4\\4&0.2\\5&0.1\end{array}\)
Using the aforesaid definition, we get the mean of random variable X as:
\(E(X) = \sum_{i=1}^n( f(x_i) \times x_i)\\\\E(X) = 1 \times 0.1 + 2 \times 0.2 + 3 \times 0.4 + 4 \times 0.2 + 5 \times 0.1\\E(X) = 0.1 + 0.4 + 1.2 + 0.8+0.5 = 3\)
Thus, the mean of the given probability distribution is 3
Learn more about expectation of a random variable here:
https://brainly.com/question/4515179
the velocity-time graph for a cycle is shown
Answers
Answer:
its not shwon btw
Step-by-step explanation:
Answer:
Step-by-step explanation:
Do you have a picture I can see?
joey, chloe and their daughter zoe all have the same birthday. joey is year older than chloe, and zoe is exactly year old today. today is the first of the birthdays on which chloe's age will be an integral multiple of zoe's age. what will be the sum of the two digits of joey's age the next time his age is a multiple of zoe's age?
Answers
The following time Joey's age is greater than Zoe's, his two numbers add up to 11 years.
Consider Chloe to be c years old and Joey to be c+1 years old. After n years, Chloe and Zoe will be n + c and n + 1 respectively.
Based on the given conditions,
(n + c) ÷ (n + 1) = 1 + [(c - 1) ÷ (n + 1)]
n is an integer for 9 non-negative integers.
C – 1 hence has 9 positive divisors.
Either \(p^{8}\) or \(p^{2} q^{2}\) is the prime factorization of c-1 < 100
Since c - 1 < 100, is
c - 1 = \(2^{2} *3^{2}\)
c - 1 = 36,
c = 36 + 1
We can calculate the coefficient,
c = 37
We can infer that Joey is 38 years old as of right now.
Assume that after k years, Joey's age is multiplied by Zoe's age, making Joey and Zoe k + 38 and k + 1 years old, respectively.
So,
We can write,
(k + 38) ÷ (k + 1) = 1 + [(38 - 1) ÷ (k + 1)]
K is an integer for some positive integers.
Since 37 can be divided by k + 1,
k = 36 is the only viable option.
Using the assumption that Joey will be k + 38 = 74 years old, the result is 7 + 4 = 11.
Therefore,
11 years is the sum of Joey's two digits the next time his age is a multiple of Zoe's age.
To learn more about information visit Age problems :
brainly.com/question/841829
#SPJ4
which table of values can be defined by the function y =6x - 2?
Answers
i need help with this question too! :(
Answer:
the answer is A
Step-by-step explanation:
Which of the following graphs is described by the function given below?
y = x^2 - 6x - 16
A. Graph A
B. Graph B
C. Graph C
D. Graph D
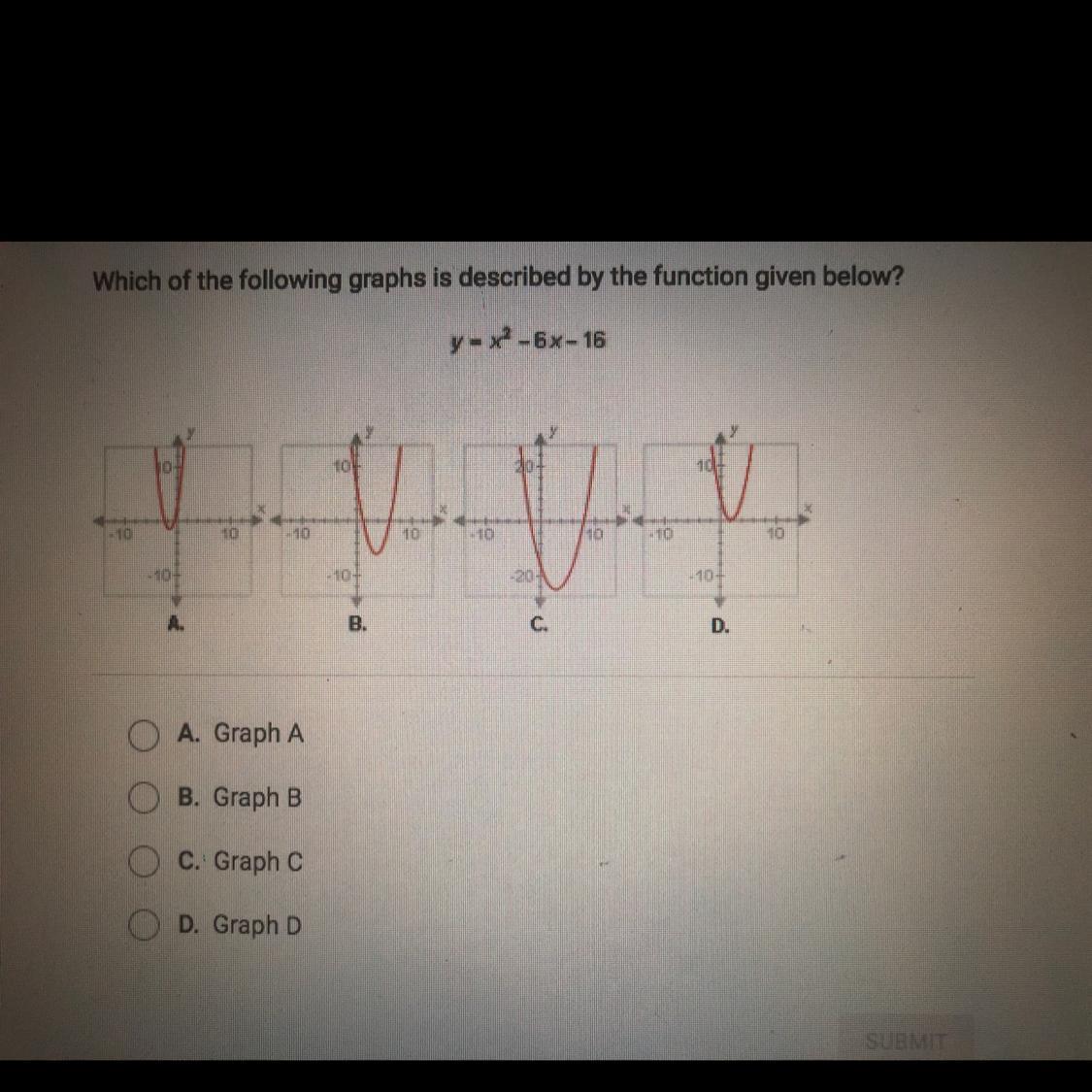
Answers
Answer:
(C).Graph C
Step-by-step explanation:
Given △abc ~ △xyz, what is the value of cos(z)? five-thirteenths five-twelfths twelve-thirteenths twelve-fifths
Answers
The value of cos(Z) is 12/13.
Since both triangles are similar, △ABC ~ △XYZ, the corresponding angles are congruent. It means:
m∠C = m∠Z, and
cos C = cos Z
The ratio for cosine is adjacent/hypotenuse. In a right triangle, the hypotenuse is the longest side, while an opposite side is the one across from a given angle, and an adjacent side is the one next to a given angle.
Since the side marked 12 is adjacent to angle C and 13 is the hypotenuse of this triangle; so, we know that:
cos C = 12/13
Thus, because of the angles and cosines for C and Z will be the same, it makes:
cos Z = cos C = 12/13
Hence, the value of cos(Z) is 12/13.
Learn more about cosines in triangle at: https://brainly.com/question/17289163
#SPJ4

What time does the clock show?
Please help I didn’t get to learn this.

Answers
Answer:
The clock shows 8:18
Step-by-step explanation:
Answer:
8:18
Step-by-step explanation:
The 16 oz jar costs per oz. and the 12oz. Jar costs per oz. Slgmund should buy the lar of mayonnaise.
Answers
Based on the given information, the cost per ounce of the 16 oz jar and the 12 oz jar is not provided. Therefore, it is not possible to determine which jar of mayonnaise Sigmund should buy.
In order to compare the cost of the two jars of mayonnaise and determine which one Sigmund should buy, we need to know the price per ounce for each jar. Without this information, we cannot make a conclusive decision.
The cost per ounce is essential because it allows us to compare the prices accurately. For example, if the 16 oz jar costs $3 and the 12 oz jar costs $2.50, we can calculate the cost per ounce for each jar. The cost per ounce for the 16 oz jar would be $3 divided by 16 oz, which is $0.1875 per ounce. Similarly, the cost per ounce for the 12 oz jar would be $2.50 divided by 12 oz, which is approximately $0.2083 per ounce.
With this information, we can determine that the 16 oz jar is more cost-effective as it has a lower cost per ounce compared to the 12 oz jar. However, without the specific prices per ounce provided in the given information, it is impossible to determine which jar of mayonnaise Sigmund should buy.
Learn more about ounce here:
https://brainly.com/question/29374025
#SPJ11
Find the slope of the line containing the pair of points.
(-3,9) and (11,10)
Answers
up one over 14 or 1/14
Complete the statements to find the measurements of La and Lb.

Answers
Answer:
see explanation
Step-by-step explanation:
∠ a and 150° are a linear pair and sum to 180° , then
∠ a + 150° = 180° ( subtract 150° from both sides )
∠ a = 30°
the sum of the 3 angles in a triangle = 180° , then
∠ b + ∠ a + 60° = 180° , that is
∠ b + 30° + 60° = 180°
∠ b + 90° = 180° ( subtract 90° from both sides )
∠ b = 90°
Ryan and Sarah collect baseball cards. Ryan has 150 baseball cards and collects 10 cards per week. Sarah has 233 baseball cards and collects 5 cards per week. After about how many weeks will Ryan and Sarah have the same number of cards?
Answers
Answer:
About 17 weeks
Step-by-step explanation:
Given
Ryan:
\(Initial = 150\)
\(Additional = 10\) (weekly)
Sarah:
\(Initial = 233\)
\(Additional = 5\) (weekly)
Required
Determine the number of weeks they have the same cards
Represent the number of weeks with w:
For Both individuals, number of card at any given week is:
\(Initial + Additional * w\)
So,
For Ryan, the expression is:
\(150 + 10 * w\)
\(150 + 10w\)
For Sarah, the expression is:
\(233 + 5 * w\)
\(233 + 5 w\)
To determine the number of weeks, we have to equate both equations:
\(150 + 10w= 233 + 5 w\)
Collect Like Terms
\(10w - 5w = 233 - 150\)
\(5w = 83\)
Solve for w
\(w = 83/5\)
\(w = 16.6\)
16.6 implies about 17 weeks, because 16.6 approximates to 17
Conclusively, Ryan and Sarah will have the same number of balls in about 17 weeks
The volume of a cone is 36piin to the power of 3. What is the volume of a cylinder with the same base and height as the cone?

Answers
Answer:
108πin³
Step-by-step explanation:
The volume of a cone = ⅓ of the volume of a cylinder
Thus, volume of cylinder = 2πr²h
Where, r = radius, h = height of cylinder.
Volume of cone = ⅓×πr²h
So therefore, the volume of a cone given = ⅓ of the volume of a cylinder with the same height and and base of the cone
Thus,
If Volume of cone = 36πin³ , volume of cylinder would be 3 × 36πin³
Volume of cylinder = 108πin³
I need help, this teacher isn't explaining things like she is supposed to

Answers
Answer:
3 and 4
Step-by-step explanation:
13 is between the perfect squares of 9 and 16, which are 3^2 and 4^2 respectively.
a closed cylindrical can has a fixed surface area s. find the ratio of its height to the diameter of its base that maximizes its volume.
Answers
The ratio of the height to the diameter that maximizes the volume of the cylindrical can is: 0.886 approximately.
Let the radius of the cylindrical can be denoted by r, and its height by h. The surface area of the can is given by:
S = 2π\(r^2\)+ 2πrh
Simplifying this expression, we get:
h = (S - 2π\(r^2\))/(2πr)
The volume of the cylindrical can is given by:
V = π\(r^2\)h
Substituting the expression for h obtained earlier, we get:
V = π\(r^2\)(S - 2π\(r^2\))/(2πr)
Simplifying this expression, we get:
V = (S/2π - \(r^2\))πr
To maximize the volume of the cylindrical can, we need to find the value of r that maximizes the above expression. We can do this by differentiating the expression with respect to r, setting it equal to zero, and solving for r:
dV/dr = (S/2π - \(2r^2\))π = 0
Solving for r, we get:
r = √(S/4π)
Substituting this value of r back into the expression for h, we get:
h = (S - 4π\(r^2\))/(4πr) = (S - S/2)/(2√(S/4π)) = √(Sπ)/2
Therefore, the ratio of the height to the diameter that maximizes the volume of the cylindrical can is:
h/2r = (√(Sπ)/2)/(2√(S/4π)) = √(π/4) = 0.886 approximately.
To learn more about cylindrical visit: https://brainly.com/question/28231934
#SPJ11
In classification analysis, we are determining the probability of an observation ________.
Answers
In classification analysis, we are determining the probability of an observation belonging to a specific class or category.
In classification analysis, we aim to assign observations to predefined classes or categories based on their features or characteristics. This analysis involves training a model on a labeled dataset, where each observation is associated with a known class.
During the training phase, the classification model learns patterns and relationships in the input data to make predictions about the class labels of unseen observations. The model estimates the probability of an observation belonging to each class based on the learned patterns.
To determine the probability of an observation belonging to a specific class, the classification model calculates a score or probability value for each class. These scores indicate the model's confidence in the prediction. The probability values are often derived from a probabilistic algorithm or a mathematical function such as logistic regression or a decision tree.
To know more about classification analysis,
https://brainly.com/question/31171180
#SPJ11
What is the surface area

Answers
Answer:
red) area = 59.2 km²
Step-by-step explanation:
area of bottom 4 x 4 = 16
area of 4 sides = 4 (1/2)(4)(5.4) = 43.2
16 + 432 = 59.2 km²
Answer:
Step-by-step explanation:
lateral area = 2(base)(slant height) = 2·4·2 = 16 km²
base area = base² = 4² = 16 km²
surface area = 16 + 16 = 32 km²
On a number line, a number, b, is located the same distance from 0 as another number, a, but in the opposite directior
The number b varies directly with the number a. For example b
22 whena=-2Which equation represents this
direct variation between a and b?
Ob=-a
Ob--a
Ob-a=0
O b-a) =0
Answers
Answer:
b=-a
Step-by-step explanation:
Becaude when b is positive a will be negative
And when b is negative a will be positive.
In order to look at specific differences between groups in a one-way ANOVA, you need to conduct: An omnibus test Post hoc comparisons A follow-up correlation O A follow-up regression Previous NE No new data to save. If you perform multiple t-tests, which of the following is true? Type I error increases Type I error decreases Type I error is not impacted 10% chance of committing Type I error Previous
Answers
If you perform multiple t-tests, the Type I error increases.
When conducting multiple t-tests, each individual test has a certain probability of committing a Type I error, which is the probability of incorrectly rejecting the null hypothesis when it is actually true. The standard threshold for Type I error is typically set at 5% (or 0.05).
However, when multiple tests are performed, the probability of committing at least one Type I error across all the tests increases. This is known as the problem of multiple comparisons or multiple testing.
The more tests you perform, the higher the likelihood of observing a significant result by chance alone, leading to an increased Type I error rate.
To address this issue, it is common to adjust the significance level (e.g., using Bonferroni correction) or conduct post hoc comparisons using methods such as Tukey's test or Bonferroni adjustment.
These methods help control the overall Type I error rate when multiple comparisons are made.
To know more about probability click here
brainly.com/question/15124899
#SPJ11
someone please help me asap. Im giving brainliest!

Answers
Answer:
C
4y=20
Hope this helped
Answer:
c
Step-by-step explanation:
need help asap pls!
Find the radius, diameter, area, and circumference of the circle
shown:

Answers
Step-by-step explanation:
Diameter =30
radius=30/2=15
area =πr²
=π×15²
= π×(15)(15)
=225π cm² or 706.95cm²
circumference C=πD
C=3.142×30cm
C=30πcm or 94.26cm
Construct both a 98% and a 80% confidence interval for B₁. B₁=46, s=5.7, SSzz = 57, n = 12 98%:
Answers
To construct a 98% confidence interval for B₁, we can use the t-distribution since the sample size is small (n = 12).
Given the sample mean (B₁ = 46), sample standard deviation (s = 5.7), and sum of squares (SSzz = 57), we can calculate the confidence interval.
The formula for a confidence interval is:
Confidence Interval = Sample Mean ± (Critical Value * Standard Error)
For a 98% confidence level and n = 12, the critical value is approximately 2.681 (obtained from a t-distribution table).
The standard error is calculated as the sample standard deviation divided by the square root of the sample size (s / √n).
Plugging in the values:
Standard Error = 5.7 / √12 ≈ 1.647
Confidence Interval = 46 ± (2.681 * 1.647)
Therefore, the 98% confidence interval for B₁ is approximately (42.21, 49.79).
In conclusion, we can be 98% confident that the true value of B₁ falls within the range of 42.21 to 49.79 based on the given sample data.
To know more about confidence interval visit :
https://brainly.com/question/15712887
#SPJ11
PLEASE HELP NO LINKS!!!!

Answers
Answer:
42 units^2
Step-by-step explanation:
the area of the triangle is 7x12/2 = 42
Find the surface area of the regular pyramid 6 cm 4cm help
Answers
The surface area of the given regular pyramid is 84 cm^2.
To find the surface area of a regular pyramid, we need to calculate the area of each face and add them together. A regular pyramid has a base that is a regular polygon, and its lateral faces are triangles that meet at a common vertex. We can use the Pythagorean theorem to find the slant height of the pyramid, which is the height of each lateral face.
Let's assume that the base of the regular pyramid is a square with side length 6 cm, and the slant height is 4 cm.
First, we need to find the area of the base of the pyramid:
Area of the base = (side length)^2
= 6 cm x 6 cm
= 36 cm^2
Next, we need to find the area of each triangular lateral face. Since the pyramid is a regular pyramid, all the triangular faces are congruent.
We can find the area of each triangular face using the formula:
Area of a triangle = (1/2) x base x height
The base of each triangular face is equal to the side length of the square base, which is 6 cm. The height of each triangular face is equal to the slant height, which is 4 cm.
Area of each triangular face = (1/2) x 6 cm x 4 cm
= 12 cm^2
Since the pyramid has 4 triangular faces, we need to multiply the area of one triangular face by 4 to get the total area of all the triangular faces:
Total area of the triangular faces = 4 x 12 cm^2
= 48 cm^2
Finally, we can find the total surface area of the pyramid by adding the area of the base and the area of the triangular faces:
Total surface area = Area of the base + Total area of the triangular faces
= 36 cm^2 + 48 cm^2
= 84 cm^2
To know more about surface area refer to
https://brainly.com/question/16519513
#SPJ11