Which expressions have a quotient of 3/5
Answers
Answer:
3/5 = 3/5
= 0.6
Related Questions
solve the inequality
2c + 1 >7
—-
3

Answers
Answer:
c > 9
Step-by-step explanation:
\(\frac{2c}{3} +1 > 7\)
To solve this, first subtract 1 from both sides
\(\frac{2c}{3} +1 > 7\\\frac{2c}{3} > 6\)
multiply both sides by 3
2c > 18
divide both sides by 2
c > 9
Hope this helps! :)
Answer:
c > 9
Step-by-step explanation:
Find the 13th term in the following
arithmetic sequence :
2, 10, 18, 26, ...
Answers
Answer:
98
Step-by-step explanation:
It goes up 8 every time.
I need help because need to bring my math grade
Mr. Anderson took Mrs. Anderson out
for a nice steak dinner. The food bill
came out to $89.25 before tax and tip.
If tax is 6% and tip is 15%, what is
the total cost?
Answers
Answer:
$108.80
Step-by-step explanation:
89.25x0.06 = $5.36 tax
89.25 + 5.36= 94.61
94.61 x 0.15 = 14.91 tip
94.61 + 14.91 = 108.80 total
A faster way: 89.25*1.06*1.15=108.80
for a test of hypotheses to compare two means based on independent samples, what happens to the likelihood of rejecting the null hypothesis for the action/change below, holding all other ideas/terms constant? b. decrease the sample sizes
Answers
The larger the Type I error, or alpha, for a test of hypotheses comparing two means based on independent samples, the more likely we are to reject the null hypothesis.
A smaller sample size will result in a bigger standard error and smaller test statistic, which will increase the p-value and decrease the likelihood that the null hypothesis will be accepted.
We are less likely to reject the null hypothesis as the sample standard deviation rises because the bigger the standard error, the lower the test statistic, and the larger the p-value. Using sample data, hypothesis testing is done to determine if a claim is plausible.
The test offers proof that the hypothesis is plausible in light of the available facts. A random sample of the population being studied is measured and examined by statistical analysts in order to test a hypothesis.
To learn more about hypothesis
https://brainly.com/question/17173491
#SPJ4
Determine whether the following statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement. Because there are 3 feet in one yard, there are also 3 square feet in one square yard. Question content area bottom Part 1 Choose the correct answer below. A. The statement is true. B. The statement is false. Because there are 3 feet in one yard, there are 27 square feet in one square yard. C. The statement is false. Because there are 3 feet in one yard, there are 6 square feet in one square yard. D. The statement is false. Because there are 3 feet in one yard, there are 9 square feet in one square yard.
Answers
The correct option regarding the scale factor and the statement in this problem is given as follows:
D. The statement is false. Because there are 3 feet in one yard, there are 9 square feet in one square yard.
How to obtain the correct scale factor?The scale factor between the length dimensions of the yard are given as follows:
3 feet = 1 yard.
(as these length dimensions are given in yards).
Then for the square units, the correct scale factor is found applying the proportion as follows:
(3 feet)² = (1 yard)².
9 feet squared = 1 square yard.
Hence the statement given in this problem, that because there are 3 feet in one yard, there are also 3 square feet in one square yard, is false, and the correct option is given by option D.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Given: rho_e (x,y,z)=2x+3y−4z(C/m) find the charge on the line segment extending from (2,1,5) to (4,3,6)
Answers
The charge on the line segment extending from (2,1,5) to (4,3,6) is determined by finding the line integral of the electric field along that line.
This line integral can be calculated by parameterizing the line segment and computing the integral using the formula:∫_a^b E·dswhere E is the electric field, s is the position vector along the line, and a and b are the starting and ending points of the line.
To parameterize the line segment, we can use the equation:r(t)=(2,1,5)+t(2,2,1)where 0 ≤ t ≤ 1. This gives us a point on the line for each value of t, and the vector (2,2,1) gives us the direction of the line. We can then calculate the electric field at each point along the line .
To know more about charge visit:
https://brainly.com/question/13871705
#SPJ11
A rocket is launched from the ground. It reaches a maximum height of 45 meters in 3 seconds and then lands back on the ground after 6 seconds. What is the function, written in standard form,
that models the trajectory of the rocket? (use shift 6 for the power and no spaces)
f(x) = type your answer...
Answers
Check the picture below.
so from the provided information, we can say that the parabola has a vertex at (3 , 45) and it has a zero at (6 , 0) or we can say is just another point at (6 , 0)
\(~~~~~~\textit{vertical parabola vertex form} \\\\ y=a(x- h)^2+ k\qquad \begin{cases} \stackrel{vertex}{(h,k)}\\\\ \stackrel{a~is~negative}{op ens~\cap}\qquad \stackrel{a~is~positive}{op ens~\cup} \end{cases} \\\\[-0.35em] ~\dotfill\)
\(\begin{cases} h=3\\ k=45\\ \end{cases}\implies y=a(~~x-3~~)^2 + 45\hspace{4em}\textit{we also know that} \begin{cases} x=6\\ y=0 \end{cases} \\\\\\ 0=a(6-3)^2+45\implies -45=9a\implies \cfrac{-45}{9}=a\implies -5=a \\\\\\ ~\hfill {\Large \begin{array}{llll} y=-5(x-3)^2 + 45 \end{array}} ~\hfill\)

Si un triángulo tiene una hipotenusa de 15 cm y un cateto que mide 12 cm, ¿cual es la longitud del otro cateto?
A) 81 m
B) 19.2 cm
C) 6 cm
¡AYUDA!
Answers
Answer:
9cm
Explicación:
El teorema de pitagoras nos dice que la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado:
\(c^{2} =a^{2} + b^{2}\)
Donde c es la hipotenusa y a y b son los catetos.
Por lo cual, podemos reemplazar c por 15cm y a por 12cm :
\(15^{2} =12^{2} +b^{2}\)
Finalmente , debemos resolver la ecuación para b, así que b es igual a :
\(225=144+b^{2} \\225-144=144+b^{2} -144\\81=b^{2} \\\sqrt{81} =b\\9=b\)
Por lo tanto, la longitud del otro cateto es 9 cm
21 meters is the same as how many feet?
Hint: 1 m ≈ 3.3 ft
Round your answer to the nearest tenth.
Answers
Answer:
69
Step-by-step explanation:
3.3x21=69.3
The owner of two grocery stores recorded the number of shoppers at each store for 10 days. On day 5, Store B had a sale. The number of shoppers per day at the stores are shown in the table.

Answers
Answer:
Step-by-step explanation:
IIncrease decrease decrease
If the population of a small town satisfies the exponential model A = 100.01), where is measured in years, how long will it take for the town's population to increasefrom 10,500 to 13,650? Round your answer to two decimal placesAnswerKeypad

Answers
We know that the expression for the population is given by:
\(A=A_0e^{0.015t}\)We want to know how long it takes to increase the population from 10500 to 13650. This means that we need to find the time it takes for the population to increase 3150; since this does not depends on the initial population but just in the exponential rate we have:
\(\begin{gathered} e^{0.015t}=3150 \\ 0.015t=\ln3150 \\ t=\frac{1}{0.015}\ln3150 \\ t=537.01 \end{gathered}\)Therefore, it will take 537.01 years to increase the population.
a college professor conducted a survey in order to assess how much money nursing majors spend on course material compared to all other majors. to do so, she selected a random sample of 34 students. each student was classified as a nursing major or as a non-nursing major. they were then asked how much they spent on books and other materials required for their courses this semester. here are parallel boxplots summarizing the responses.
Answers
Option D. The median cost of course materials for nursing majors is over $300 more than the median cost of course materials for non-nursing majors.
The given boxplots show the circulation of the expense obviously materials for nursing majors and non-nursing majors. From the plots, we can reason that the scope of the circulation of the expense obviously materials for nursing majors is like that of non-nursing majors, as the most extreme and least qualities are around at a similar level. We can likewise infer that the most extreme expense for non-nursing majors is more prominent than the middle expense for nursing majors.
Also, the inconstancy of the expense obviously materials for the center half of nursing majors is more noteworthy than the fluctuation of the center half for non-nursing majors, as the cases for nursing majors are more extensive. In any case, we can't reason that the middle expense obviously materials for nursing majors is more than $300 more than the middle expense obviously materials for non-nursing majors, as the medians are not straightforwardly named and their division isn't plainly shown. At last, we can see that the study included 17 nursing majors and 17 non-nursing majors.
To learn more about statistics and data analysis, refer:
https://brainly.com/question/18351121
#SPJ4
The complete question is:
A college professor conducted a survey in order to assess how much money nursing majors spend on course material compared to all other majors. To do so, she selected a random sample of 34 students. Each student was classified as a nursing major or as a non-nursing major. They were then asked how much they spent on books and other materials required for their courses this semester. Shown above are parallel boxplots summarizing the responses. Based upon the boxplots, which of the following statements cannot be concluded?
A. The range of the distribution of the cost of course materials for nursing majors is about the same as that of non-nursing majors.
B. The maximum cost for non-nursing majors is greater than the median cost for nursing majors.
C. The variability of the cost of course materials for the middle 50% of nursing majors is greater than the variability of the middle 50% for non-nursing majors.
D. The median cost of course materials for nursing majors is over $300 more than the median cost of course materials for non-nursing majors.
E. The boxplots reveal that 17 students are nursing majors and 17 students are non-nursing majors
Please answer A,B,C &D. Question is in the pic.

Answers
Answer:
A. same point.
b. in center
c. triangle centroid
d. single point
Which value of x makes the equation 1.25(4x - 10) = 7.5 true
Answers
Answer: x = 4
Step-by-step explanation:
1.25(4x-10)=7.5
5x-12.5 = 7.5
5x = 20
x = 4
Answer:
x=4
Step-by-step explanation:
1.25(4(4)-10)=7.5
1.25(16-10)=7.5
1.25(6)=7.5
7.5=7.5
TRUE
Find three consecutive positive odd integers such
that the square of the smallest exceeds twice the
largest by 7.
Answers
Answer:
5, 7, 9
Step-by-step explanation:
You want three consecutive positive odd integers such that the square of the smallest exceeds twice the largest by 7.
SetupLet x represent the middle of the integers. Then x-2 is the smallest, and x+2 is the largest. The given relation is ...
(x -2)² -2(x +2) = 7
SolutionEliminating parentheses gives ...
x² -4x +4 -2x -4 = 7
x² -6x -7 = 0 . . . . . . . . . subtract 7, simplify
(x -7)(x +1) = 0 . . . . . . . factor
Values of x that make the factors zero are solutions to this equation:
x -7 = 0 ⇒ x = 7
x +1 = 0 ⇒ x = -1
The positive odd numbers are 5, 7, 9.
__
Check
5² -2(9) = 25 -18 = 7 . . . . as required
2.
Q. 24,000 grams
=
kilograms
Answers
Answer:
24 kilograms
Step-by-step explanation:
one kilogram is 1000 grams
The zeroes of t' are - 3. 1, and 4 so the local extrema are located at these points. Choose the correct answer below. O A. True. The zeros of f' are local extrema so long as the denominator is nonzero at those points. OB. False. The zeros of f' are the inflection points of f. OC. True The zeros off' are the local extrema off. OD. False. A zero off' is a critical point and is a local extremum so long as f'(x) changes sigh Take, for example, the function f(x)=(x + 3)º(x-1)*(x-4)
Answers
The correct answer is: OC. True. The zeros of f' are the local extrema of f.
By the first derivative test, if f'(x) changes sign from positive to negative at a critical point, then there is a local maximum at that point. If f'(x) changes sign from negative to positive at a critical point, then there is a local minimum at that point.
In this case, the zeros of f' are -3, 1, and 4, which are the critical points of f. Therefore, by the first derivative test, there are local extrema of f at these points.
Option A is incorrect because the denominator of f' is not relevant in determining the local extrema of f. Option B is incorrect because the zeros of f' are not necessarily inflection points. Option D is incorrect because a zero of f' is not necessarily a local extremum unless f'(x) changes sign at that point.
Learn more about zeros here:
https://brainly.com/question/29120033
#SPJ11
PLEASEEE HELP!!!!
!!!ILL GIVE >>BRAINLIST<

Answers
Answer:
Step-by-step explanation:

a dataset has mean and standard deviation and median m. we transform the dataset by calculating the following value for each datapoint with value xi: (a and b are both positive numbers.) what is the variance of the new dataset? group of answer choices
Answers
Our new measures of central tendency and spread are Mean: (9+9+13+15+19)/5=13(9+9+13+15+19)/5=13.
What is mean?In mathematics and statistics, the concept of mean is crucial. The most typical or average value among a group of numbers is called the mean.It is a statistical measure of a probability distribution's central tendency along the median and mode. It also goes by the name "expected value."There are different ways of measuring the central tendency of a set of values. There are multiple ways to calculate the mean. Here are the two most popular ones:Arithmetic mean is the total of the sum of all values in a collection of numbers divided by the number of numbers in a collection.acc to our question-
Median: 1313Mode: 99Range: 19-9=1019−9=10learn more about mean click here:
brainly.com/question/1136789
#SPJ4
how do you convert fractions to decimals?
Answers
Answer:
divide the fractions
Step-by-step explanation:
lets say we have 23/5
we can divide 23 by 5 and get a decimal of 4.6
or lets say we got 1/5
divide 1 by 5 and you will get 0.2
7. outliers are defined as data values that are above the right fence q3 1.5(iqr) or below the left fence q1 - 1.5(iqr), where iqr is the interquartile range. find the probability that when a value is randomly selected from a normal distribution, it will be counted as an outlier. Round your answers to 3 decimal places. Hint. Consider the standard normal distribution. Find P(Z> right fence or Z< left fence).
Answers
When a value is randomly selected from a normal distribution, find the probability that it will be counted as an outlier. Rounded to three decimal places, the answer is 0.007.
Consider the standard normal distribution. To find P(Z > right fence or Z < left fence), we must first find the value of the right and left fences. Outliers are defined as data values that are above the right fence q3 1.5(iqr) or below the left fence q1 - 1.5(iqr), where iqr is the interquartile range. The interquartile range can be calculated using the following formula:IQR = Q3 – Q1where Q3 and Q1 are the 75th and 25th percentiles, respectively.To calculate the right fence, we use the formula:
Right fence = Q3 + 1.5(IQR).
To calculate the left fence, we use the formula:
Left fence = Q1 - 1.5(IQR).
Since the problem only provides information about the standard normal distribution, we will use Z-scores to find the probability that a value is an outlier. We use the Z-score formula:
Z = (x - μ) / σ where x is the observed value, μ is the mean, and σ is the standard deviation. Because we are using the standard normal distribution, the mean is zero and the standard deviation is one.We now have all of the information we need to calculate the probability of an outlier.
P(Z > right fence or Z < left fence) = P(Z > right fence) + P(Z < left fence).We first calculate P(Z > right fence):P(Z > right fence) = P(Z > (Q3 + 1.5(IQR) - μ) / σ) = P(Z > (Q3 + 1.5(IQR)))
Using the standard normal distribution table, we look up the value of Z for (Q3 + 1.5(IQR)) to get: P(Z > right fence) = P(Z > 2.698) = 0.0034. Next, we calculate P(Z < left fence): P(Z < left fence) = P(Z < (Q1 - 1.5(IQR) - μ) / σ) = P(Z < (Q1 - 1.5(IQR))). Using the standard normal distribution table, we look up the value of Z for (Q1 - 1.5(IQR)) to get:P(Z < left fence) = P(Z < -2.698) = 0.0034. Therefore, P(Z > right fence or Z < left fence) = 0.0034 + 0.0034 = 0.0068, which, rounded to three decimal places, is 0.007.
Learn More About Standard Deviation: https://brainly.com/question/4079902
#SPJ11
To find the probability that a value randomly selected from a normal distribution will be counted as an outlier, we need to convert the values of the fences into z-scores using the standard normal distribution.
The formula for finding the z-score of a value x is:
z = (x - μ) / σ
where μ is the mean and σ is the standard deviation of the distribution.
For the right fence, we have:
right fence = Q3 + 1.5(IQR)
We can convert Q3 and IQR into z-scores using the formula above, since they are also measures of central tendency and dispersion.
z(Q3) = (Q3 - μ) / σ
z(IQR) = IQR / σ
Using the properties of quartiles and the fact that the normal distribution is symmetric, we know that Q3 is located at approximately z = 0.67.
To find IQR, we need to calculate the difference between the 75th and 25th percentiles:
IQR = Q3 - Q1
Since the normal distribution is symmetric, we can assume that Q1 is located at approximately z = -0.67.
Therefore:
z(Q3) = (0.67 - 0) / 1 = 0.67
z(IQR) = (0.67 - (-0.67)) / 1 = 1.34
z(right fence) = z(Q3) + 1.5 * z(IQR) = 0.67 + 1.5 * 1.34 = 2.67
Similarly, we can calculate the z-score for the left fence:
left fence = Q1 - 1.5(IQR)
z(left fence) = z(Q1) - 1.5 * z(IQR) = -0.67 - 1.5 * 1.34 = -3.00
Now that we have the z-scores for the fences, we can use the standard normal distribution table or calculator to find the probabilities:
P(Z > 2.67) = 0.003
P(Z < -3.00) = 0.001
The probability of randomly selecting a value that is an outlier is therefore:
P(Z > 2.67 or Z < -3.00) = P(Z > 2.67) + P(Z < -3.00) = 0.003 + 0.001 = 0.004
Therefore, the probability of randomly selecting a value from a normal distribution that will be counted as an outlier is 0.004, rounded to 3 decimal places.
To learn more about ''outliers are defined as data values'' visit : https://brainly.com/question/27836059
#SPJ11
Find the slope of the line y=1/6+3/2
Answers
Answer:
1/6 if you meant to put an X afterwards. If not, there is no slope.
Step-by-step explanation:
Find A U { }. If A is any given set
Answers
Answer:
A U { } = A
Step-by-step explanation:
Union is one of the operations that are performed on sets. In union, the elements of involved sets are combined and repetitive elements are removed (written only once)
Given
A U { } = ?
Whenever union will be taken of any set and empty set the answer will be the set.
Similarly, when union of set A will be taken with empty set the result will be set A.
Hence,
A U { } = A
I really need help Please

Answers
Answer:
The tree was 5 feet when he bought it and it grew one foot every year.
I believe the equation would be h=t+5
Step-by-step explanation:
The answer would be h=t+5 because the height equals the year plus five.
Find the Least Common Multiple of 4 and 16.
A.16
B.2
C.4
D.8
Answers
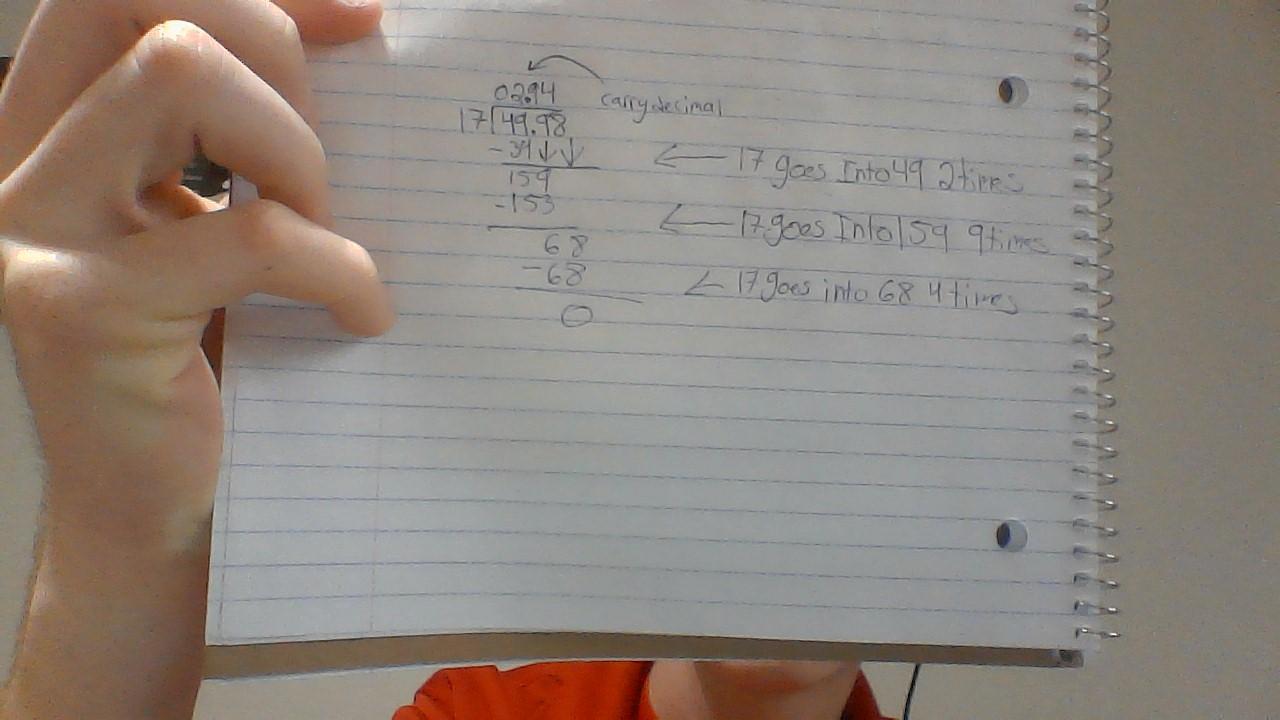
49.98 ÷ 17 = ? (show ur work)
Answers
Answer:
2.94
Step-by-step explanation:
In the picture below
What is the value of m, when 2⁶ x 4 = 418
Answers
Answer:
The answer should be 3.3/4
Step-by-step explanation:
Suppose a normally distributed set of data with 2400 observations has a mean of 162 and a standard deviation of 11. Use the 68-95-99.7 Rule to determine the number of observations in the data set expected to be below a value of 195. Round your result to the nearest single observation. Hint: This problem is asking for how many observations, not the percent. Answer= Tip: Don't round any probabilities or percentages in your calculations. Keep all decimal places and round at the END of the problem. Suppose a normally distributed set of data with 4000 observations has a mean of 137 and a standard deviation of 19. Use the 68-95-99.7 Rule to determine the number of observations in the data set expected to be above a value of 118. Round your answer to the nearest whole value. Hint: This problem is asking for how many observations not the percent.
Answers
Rounding to the nearest whole value, we get the estimated number of observations above 118 as 2940.
To determine the number of observations expected to be below a certain value using the 68-95-99.7 Rule, we need to find the area under the normal distribution curve up to that value.
For the first scenario:
Mean (μ) = 162
Standard deviation (σ) = 11
Value to evaluate (x) = 195
We want to find the area under the curve to the left of x = 195. This corresponds to the cumulative probability of a value being less than 195 in a normal distribution.
Using a standard normal distribution table or a calculator, we can find that the cumulative probability for x = 195 is approximately 0.961. This means that about 96.1% of the observations are expected to be below 195.
To find the number of observations, we multiply the cumulative probability by the total number of observations:
Number of observations = 0.961 * 2400 = 2306.4
Rounding to the nearest single observation, we get the estimated number of observations below 195 as 2306.
For the second scenario:
Mean (μ) = 137
Standard deviation (σ) = 19
Value to evaluate (x) = 118
We want to find the area under the curve to the right of x = 118. This corresponds to the cumulative probability of a value being greater than 118 in a normal distribution.
Using the same approach, we can find that the cumulative probability for x = 118 is approximately 0.735. This means that about 73.5% of the observations are expected to be above 118.
To find the number of observations, we multiply the cumulative probability by the total number of observations:
Number of observations = 0.735 * 4000 = 2940
learn more about whole value here
https://brainly.com/question/12086644
#SPJ11
A submarine dives below the surface, heading downward in two moves. If each move downward was 355 feet, where is the submarine after it is finished diving?
Answers
Answer: The submarine would be 710 feet below the surface after it is finished diving.
Step-by-step explanation:
Given: Each move downward was of 355 feet
If the submarine dives below the surface, heading downward in two moves.
Then, the total distance moved by submarine = 2 (355) feet
= 710 feet
Therefore, the submarine would be 710 feet below the surface after it is finished diving.
Which processing conditions are required for a rapid sintering densification with high final density? Lütfen birini seçin: A. High green density and Small pore size distribution O B. Low green density and Wide particle size distribution O C. Small pore size and Agglomerated powder O D. Low packing density and Narrow particle size distribution
Answers
The processing conditions required for rapid sintering densification with high final density are high green density and small pore size distribution. Option (A) is the correct choice.
To achieve rapid sintering densification with high final density, certain processing conditions need to be met. One important factor is green density, which refers to the density of the compacted powder before sintering. High green density provides a higher starting point for densification during sintering and allows for more efficient pore elimination. Therefore, high green density is preferred over low green density.
Another crucial factor is the pore size distribution. Small pore size distribution is desirable because it allows for easier elimination of pores during sintering. Small pores can be more readily closed off and eliminated, resulting in higher final density.
Options (B), (C), and (D) do not satisfy the requirements for rapid sintering densification with high final density. Low green density, wide particle size distribution, agglomerated powder, and narrow particle size distribution can impede the densification process and result in lower final density.
Therefore, option (A) - high green density and small pore size distribution - is the correct choice for achieving rapid sintering densification with high final density.
Learn more about distribution here:
https://brainly.com/question/29664127
#SPJ11