Answers
Answer:
x=20
3x= 3(20)=60
4x= 4(20)=80
Step-by-step explanation:
The angles CD is 90 degrees because the small square indicates
it. Angles AD are a straight angle, therefore all the other angles within A to D, must equal 180 degree. (straight line/angle=180 degrees).
so AB + 70+ 90= 180 degrees
AB= 180 -70-90
AB=20
x=20
3x= 3(20)=60
4x= 4(20)=80
Answer:
Step-by-step explanation:
x + 3x + 4x + 70° + 90° = 360° ( being complete turn )
8x + 160° = 360°
8x = 360° - 160°
8x = 200°
x = 25°
3x = 3 * 25°= 75°
4x = 4 * 25° = 100°
Related Questions
Which of the following refers to the type of statistical methods used to draw conclusions about the population based on a sample?
Population methods
Sampling methods
Descriptive statistics
Inferential statistics
Answers
The type of statistical methods used to draw conclusions about the population based on a sample is called inferential statistic.
Statistical inference refers to the process of generating inferences about a population from a sample or subset of the data. The goal of inferential statistics is to extrapolate from sample data to the population as a whole by comparing the parameters of multiple samples. Two major categories of inferential statistics use distinct strategies to extrapolate information from samples of the population. These are regression analysis and hypothesis testing. Inferential statistics, including hypothesis testing, examines sample data to draw conclusions about the whole population. It entails establishing a null hypothesis and an alternative hypothesis, then doing a statistical test of significance to determine which one is more likely to be correct. The impact of one variable on another can be measured with the use of regression analysis.
To learn more about inferential statistics, click here:
https://brainly.com/question/28352023
#SPJ4
To find the x-value of the midpoint, you add half the difference between the
x-values of (1, 7) and (3, 11) to 1, which is the smaller of the two x-values. The
complete expression for the x-value is 1 + __
1
2(3 − 1). What expression do you get
if you add half the difference between the y-values of (1, 7) and (3, 11) to 7 to
find the y-value of the midpoint?
Answers
The x and the y values of the midpoint are 2 and 9, respectively
How to determine the x and the y values of the midpoint?The points are given as:
(1, 7) and (3, 11)
The rules to determine the x and the y values of the midpoint are given as:
Add half the difference between the x-values or y values of (1, 7) and (3, 11) to the smaller of the two x-values or y values
So, we have:
x value
Midpoint = 1/2(3 - 1) + 1
Evaluate
Midpoint = 2
y value
Midpoint = 1/2(11 - 7) + 7
Evaluate
Midpoint = 9
Hence, the x and the y values of the midpoint are 2 and 9, respectively
Read more about midpoints at:
https://brainly.com/question/16866169
#SPJ1
What is the correct value of x
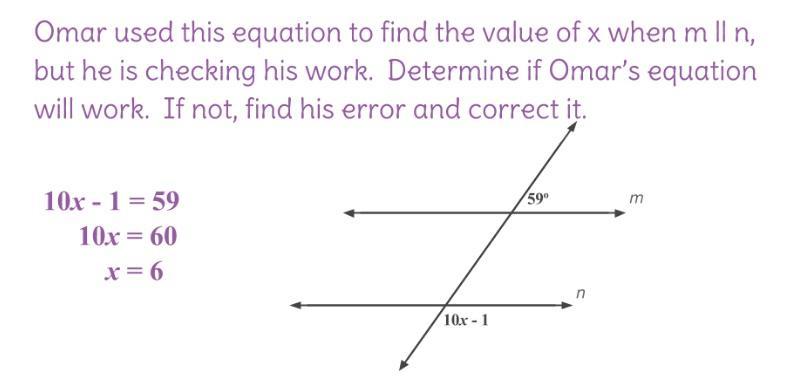
Answers
Answer:
he looks right
_________________
Fill in the blank to find the y-intercept.
(0,_____)

Answers
Answer:
-2
Step-by-step explanation:
Answer:
-2
Step-by-step explanation:
the y intercept is the point on the graph where the line crosses the x axis
Let f be the function defined by f(x)=ax2+bx+22x2−8, where a and b are constants. The graph of f has a horizontal asymptote at y=3, and f has a removable discontinuity at x=2.
Show that a=6 and b=−13.
Answers
The value of a and b are 6 and -13.
What is a function?A function is defined as a relation between a set of inputs having one output each.
We have,
f(x) = ax² + bx + 2 / 2x² - 8
f(x) horizontal asymptote:
y = 3
f(x) has a removable discontinuity:
x = 2
Now,
f(x) has a horizontal asymptote if:
Degree of the denominator = Degree of the numerator
It is given by:
y = coefficient of higher x of the numerator ÷ coefficient of higher x in the denominator
We have,
y = a / 2
3 = a / 2
a = 6
Removable discontinuity at x = 2 means:
Numerator of f(x) = 0
We have,
ax² + bx + 2 = 0
6 x (2)² + b x 2 + 2 = 0
24 + 2b + 2 = 0
2b = -26
b = -13
Thus the value of a and b are 6 and -13.
Learn more about functions here:
https://brainly.com/question/13240157
#SPJ1
Aris and Josiah are reading a 50-page book for their ELA class. Aris wants to know what page Josiah is reading. Josiah gives her two hints: 1. The product of the two page numbers he can see is 930. 2. The page he is reading is an odd numbered page.
Answers
Answer:
31
Step-by-step explanation:
Let x and (x + 1) be the page numbers Josiah can see
Hint 1: x(x + 1) = 930
⇒ x² + x = 930
⇒ x² + x - 930 = 0
Using quadratic formula,
\(x = \frac{-b\pm\sqrt{b^2 -4ac} }{2a}\)
a = 1, b = 1 and c = -930
\(x = \frac{-1\pm\sqrt{1^2 -4(1)(-930)} }{2(1)}\\\\= \frac{-1\pm\sqrt{1 +3720} }{2}\\\\= \frac{-1\pm\sqrt{3721} }{2}\\\\= \frac{-1\pm61 }{2}\\\)
\(x = \frac{-1-61 }{2}\;\;\;\;or\;\;\;\;x= \frac{-1+61 }{2}\\\\\implies x = \frac{-62 }{2}\;\;\;\;or\;\;\;\;x= \frac{60 }{2}\\\\\implies x = -31\;\;\;\;or\;\;\;\;x= 30\)
Sice x is a page number, it cannot be negative
⇒ x = 30 and
x + 1 = 31
The two pages Josiah can see are pg.30 and pg.31
Hint 2: The page he is reading is an odd number
Out of the pages 30 and 31, 31 is an odd number
Thereofre, Josiah is reading page 31
Ashley mixes two types of soft drinks with different types of concentration: one soft drink has 20% sugar and the other drink has 45% sugar.
Each can has 250 milliliters of soda drink .
What is the sugar concentration of the mixed soft drink
Answers
Answer:
32.5% sugar
Step-by-step explanation:
You want to know the sugar concentration in the mix of two 250-mL cans of soft drink, one of which is 20% sugar, and the other of which is 45% sugar.
Weighted averageThe fraction of sugar in the mix is the weighted average of the fractions in the contributors. The weights are the volumes. Since the volumes are equal, the weights are equal, so the fraction in the final mix is simply the average of the two fractions:
(20% +45%)/2 = 65%/2 = 32.5%
The sugar concentration of the mixed soft drink is 32.5%.
HELPP I DONT UNDERSTAND THIS

Answers
Answer:
5/14
Step-by-step explanation:
1/7 = 2/143/14 = 3/14Add them together: 2/14 + 3/14 = 5/14I hope this helps!
I need help with this math

Answers
Answer:
500 and 4.3
Step-by-step explanation:
A decigram is one-tenth of a gram and a kilometer is one-thousandth of a meter. Using this information, we must multiply the given amounts by the values.
5000 × 0.1 = 500
4300 × 0.001 = 4.3
Thus, the answers [in order] are 500 and 4.3
Hope this helps and feel free to ask any questions.
Help solve the question please.

Answers
Answer:
\(v = \sqrt{\dfrac{a -cb}{c\sqrt{2}} } = \dfrac{\sqrt{ a -cb}}{\sqrt{c}\sqrt[4]{2} }\)
Step-by-step explanation:
\(c = \dfrac{a}{b+\sqrt{2v} }\)
The equation for \(v\) will be
\(c = \dfrac{a}{b+\sqrt{2v} } \implies c(b+\sqrt{2v}) = a \implies cb + c\sqrt{2v} = a\)
Once \(\sqrt{2v} = \sqrt{2} \sqrt{v}\)
\(cb + c\sqrt{2}\sqrt{v} = a \implies c\sqrt{2}\sqrt{v} = a -cb \implies \sqrt{v} =\dfrac{a -cb}{c\sqrt{2}}\)
Square both sides
\(\sqrt{v} =\dfrac{a -cb}{c\sqrt{2}} \implies v = \sqrt{\dfrac{a -cb}{c\sqrt{2}} } = \dfrac{\sqrt{ a -cb}}{\sqrt{c}\sqrt[4]{2} }\)
Step-by-step explanation:
Multiply both sides of the equation by \(b + \sqrt{2\nu}\) to get
\(cb + c\sqrt{2\nu} = a\)
Put the cb term to the right hand side and then divide by c to get
\(\sqrt{2\nu} = \dfrac{a - cb}{c}\)
Taking the square of the equation, we get
\(2\nu = \left(\dfrac{a - cb}{c}\right)^2\)
Finally, dividing the equation by 2 and we get an equation for \(\nu.\)
\(\nu = \dfrac{1}{2}\left(\dfrac{a - cb}{c}\right)^2\)
√3 + (4 + √x + 3)² / 6 = 3

Answers
Answer: x = 1
Step-by-step explanation:
To find the factors of a polynomial from its graph, follow this rule: if the number ___ is a root of a polynomial, then x-c is a factor. (FILL IN THE WORD QUESTION)

Answers
Solution
if the number _C__ is a root of a polynomial, then x-c is a factor.
Whenever we have a polynomial
Example
\(undefined\)
Please help :solve the inequality: 6p-20>-36+10p

Answers
Answer:
c.p<-1
Step-by-step explanation:
im good at math
g(t)=−(t−1)
2
+5g, left parenthesis, t, right parenthesis, equals, minus, left parenthesis, t, minus, 1, right parenthesis, squared, plus, 5
What is the average rate of change of
�
gg over the interval
−
4
≤
�
≤
5
−4≤t≤5minus, 4, is less than or equal to, t, is less than or equal to, 5?
Answers
The average rate of change over is 1.
Given that;
the function is,
⇒ g (t) = - (t - 1)² + 5
Hence, We need to determine the average rate of change over the interval - 4 ≤ t ≤ 5.
The value of G(-4):
The value of G(-4) can be determined by substituting t = -4 in the function
⇒ g (t) = - (t - 1)² + 5
Thus, we have,
⇒ g (t) = - (-4 - 1)² + 5
⇒ g (t) = - 20
Thus, the value of G(-4) = -20
The value of G(5):
The value of G(5) can be determined by substituting t = 5 in the function , we get,
⇒ g (t) = - (t - 1)² + 5
⇒ g (t) = - (5 - 1)² + 5
⇒ g (t) = - 11
Thus, the value of G(5) is, -11
Now, Average rate of change:
The average rate of change can be determined using the formula,
⇒ G(b) - G (a) / (b - a)
where, a = - 4 and b = 5
Substituting the values, we get,
⇒ G(5) - G (-4) / (5 - (-4))
⇒ ( - 11 - (- 20)) / 9
⇒ 9/9
⇒ 1
Thus, the average rate of change over the interval is. 1.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ1
To find the slope of a curve at a given point, we simply differentiate the equation of the curve and find the first derivative of the curve, i.e., dy/dx.
Answers
To find the slope of the curve, first differentiate the equation of the curve and substitute the value of x in the result
The slope of the curve is the change in y coordinates with respect to the change in x coordinates of the line
To find the slope of the curve at a given point
First differentiate the given equation of the curve with respect to x
That is dy / dx.
The derivative of the equation of the curve is the slope of the curve.
In next step substitute the value of x in the slope of the curve
The result will be the slope of the curve at a given point
Therefore, these are the steps to find the slope of the curve
I have answered the question in general, as the given question is incomplete
The complete question is:
How to find the slope of a curve at a given point?
Learn more about slope of the curve here
brainly.com/question/4748565
#SPJ4
Using the scientific calculator or graphing calculator find the inverse tangent of the ratio. Round to the nearest degree. 3/1

Answers
Given:
The ratio is \(\dfrac{3}{1}\).
To find:
Inverse tangent of the given ratio.
Solution:
We know that,
Inverse tangent of the ratio \(\dfrac{3}{1}\) = \(\tan^{-1}\dfrac{3}{1}\)
= \(\tan^{-1}3\)
Using scientific or graphing calculator, we get
Inverse tangent of the ratio \(\dfrac{3}{1}\) = \(71.565^\circ\)
Round to the nearest degree
Inverse tangent of the ratio \(\dfrac{3}{1}\approx 72^\circ\)
Therefore, the correct option is C.
Which of the following is the product of (3x − 5) and (3x + 5)?
Answers
Answer:
\( {9x}^{2} - 30x + 25\)
\(\huge\underline\bold\blue{ƛƝƧƜЄƦ}\)
(3x + 5)(3x - 5)
By using identity
(a + b)(a - b) = a² - b²
3x² - 5²
9x² - 25
Find the circumference of c

Answers
Answer:
47.12
Step-by-step explanation:
find the area of the Shaded region below in all of the smaller squares are identical in size

Answers
Area of the shaded region = 80 in²
Explanation:The outer diagram is a square
Area of the square = length × length
length = 12in
Area of the square = 12in × 12in
Area of the square = 144in²
There are 3 smaller squares in each row and column:
The length in each row and colum = 12
the length o fone small box = 12/3 = 4
Area of the smaller box = 4in × 4in = 16 in²
There are 4 boxes unshaded
Area of 4 unshaded boxes = 4 × 16 in² = 64in²
Area of the shaded region = Area of the outer box - area of the unshaded boxes
Area of the shaded region = 144 - 64
Area of the shaded region = 80 in²
Solve the following exponential equation. Express irrational solutions in exact form and as a decimal rounded to three decimal places.What is the exact answer? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.(Simplify your answer. Type an exact answer.)What is the answer rounded to three decimal places? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.(Simplify your answer. Type an integer or decimal rounded to three decimal places as needed.)

Answers
To solve the exponential equation, we apply natural logarithm from both sides of it:
\(\begin{gathered} 4^{1-9x}=5^x \\ \ln (4^{1-9x})=\ln (5^x) \end{gathered}\)Now, we apply the power rule of the logarithms:
\(\log _b(M^p)=p\cdot\log _b(M)\Rightarrow\text{ Power rule}\)\(\begin{gathered} \ln (4^{1-9x})=\ln (5^x) \\ (1-9x)\ln (4^{})=x\ln (5^{}) \end{gathered}\)Now, we apply the distributive property on the left side of the equation:
\(\begin{gathered} 1\cdot\ln (4)-9x\cdot\ln (4^{})=x\ln (5^{}) \\ \ln (4)-9x\ln (4^{})=x\ln (5^{}) \end{gathered}\)Now, we subtract xln(5) from both sides of the equation:
\(\begin{gathered} \ln (4)-9x\ln (4^{})-x\ln (5)=x\ln (5^{})-x\ln (5) \\ \ln (4)-9x\ln (4^{})-x\ln (5)=0 \end{gathered}\)Now, we subtract ln(4) from both sides:
\(\begin{gathered} \ln (4)-9x\ln (4^{})-x\ln (5)-\ln (4)=0-\ln (4) \\ -9x\ln (4^{})-x\ln (5)=-\ln (4) \end{gathered}\)Now, we factor x on the left side:
\(\begin{gathered} x(-9\ln (4^{})-\ln (5))=-\ln (4) \\ \text{ Divide by }-9\ln (4)^{}-\ln (5)\text{ from both sides} \\ \frac{x(-9\ln(4^{})-\ln(5))}{(-9\ln(4^{})-\ln(5))}=\frac{-\ln(4)}{(-9\ln(4^{})-\ln(5))} \\ x=\frac{-\ln(4)}{(-9\ln(4^{})-\ln(5))} \\ x=\frac{-\ln(4)}{-(9\ln(4^{})+\ln(5))} \\ x=\frac{\ln(4)}{9\ln(4^{})+\ln(5)} \end{gathered}\)Thus, the exact solution is:
\($$\boldsymbol{x=\frac{\ln(4)}{9\ln(4^{})+\ln(5)}}$$\)And the solution rounded to three decimal places is:
\($$\boldsymbol{x=0.098}$$\)The volume of a sphere is 4500cm. What is the surface area of the sphere to the nearest whole number?
Answers
The surface area of the sphere, to the nearest whole number, is 1318 cm².
How to determine the surface area of a sphere?A sphere is simply a three-dimensional geometric object that is perfectly symmetrical in all directions.
The volume of a sphere is expressed as:
Volume = (4/3)πr³
The surface area of a sphere is expressed as:
SA = 4πr²
Where r is the radius of the sphere and π is the mathematical constant pi.
Given that the volume V is 4500 cm³.
First, we solve for the radius:
Volume = (4/3)πr³
4500 = (4/3)πr³
4500 × 3 = 4πr³
13500 = 4πr³
r³ = 13500/4π
r = ∛( 13500/4π )
Now that we have the radius, we can calculate the surface area of the sphere using the formula:
SA = 4πr²
Substituting the radius we found:
SA = 4 × π × ∛( 13500/4π )²
SA = 1318 cm²
Therefore, the surface area is approximately 1318 cm².
Learn more about volume of hemisphere here: brainly.com/question/22886594
#SPJ1
The radius of inscribed circle is 10 what is the perimeter of square cabd
Answers
Answer:
P=80
Step-by-step explanation:
R= 10
P = R*2 *4
P of a square = 10*2 *4 = 80
Just divide by any fraction of the squares ratio.
ie) if square = 2/3 of the length of the circle then 80 x 2/3 = 53.333...
ie) if square = 3/4 of the length of the diameter of the circle then 80 x 3/4 = 60
As 3/4 pf 10 = 7.5
7.5 * 2 = 15
15* 4 = 60
Howver the square is outside of the circle as described circle inscribed exactly how much if it fits exactly then the length will be same as circles diameter = 10*2 = D;20.
20 *4 = 80. P;80
Etc.
express the following ratio as fraction and reduce them to their simplest form 200 meters : 1.4 kilometre
Answers
Step-by-step explanation:
200m:1.4km
200m:1400m
1:7
Two cars leave towns 850 kilometers apart at the same time and travel toward each other. One car's rate is 16 kilometers per hour less than the other's. If they meet in 5 hours, what is the rate of the slower car? Do not do any rounding.
Answers
Answer:9.5
Step-by-step explanation:
Complete the table and fill in the last

Answers
Answer:
Its will be 2/3
Step-by-step explanation:
hope it helps you
Answer:
3/5…...........….........
Help help math math math

Answers
\(y=-6x+12\\\\\text{When}~ x = -1\\\\y=-6(-1)+12 = 6+12 = 18\)
Select all the intervals where f is decreasing

Answers
One Answer: Choice C) 0 < x < 1
==================================================
Explanation:
Let's go through the answer choices one at a time.
Choice A represents an increasing interval since the graph goes uphill as we move from left to right. The line through the points (-2, f(-2)) and (-1.5, f(-1.5)) has a positive slope. We can rule out choice A.Choice B is a similar story to choice A. The graph goes uphill when we move from x = -1 to x = 0, so the graph is increasing on the interval -1 < x < 0. We can rule out choice B.In contrast, choice C is a decreasing interval. Going from x = 0 to x = 1 has us move downhill. Choice C is the only answer.Choice D is false because choice C was shown to be true.The correct option is C
What is a decreasing function?A function whose value decreases as the independent variable increases over a given range is called a decreasing function.
Considering the options :
A) it represents an increasing interval since the graph goes uphill as we move from left to right. The line through the points (-2, f(-2)) and (-1.5, f(-1.5)) has a positive slope. We can rule out choice A.
B) It is a similar story to choice A. The graph goes uphill when we move from x = -1 to x = 0, so the graph is increasing on the interval -1 < x < 0. We can rule out choice B.
In contrast, C is a decreasing interval. Going from x = 0 to x = 1 has us move downhill. Choice C is the only answer.
Hence, the correct option is 0 < x < 1
Learn more about decreasing function, click;
https://brainly.com/question/14330051
#SPJ5
Multiple choice (you can choose more than one)

Answers
Answer:
A and D
Step-by-step explanation:
Lucy invested for 15 years at 2.8%, compounded annually and ended with an account balance of $2250. What was her initial deposit?
Answers
Answer:1244
Step-by-step explanation:
Answer:
Step-by-step explanation:
Use the formula for calculating compound interest PN=P0(1+rk)Nk where N is the unknown, PN=2250, k=1, N=15, and r=0.028. Substitute the values into the formula and simplify.
2250=P(1+0.0281)1⋅15
2250=P(1.028)15
2250=P(1.5132...)
1486.91=P
Rounded to the nearest dollar, Lucy's initial deposit was $1487.
The length of a rectangle is six times its width. The area of the rectangle is 384 square centimeters. Find the dimensions of the rectangle.
Answers
Answer:
Width = 8 cm
Length = 48 cm
Step-by-step explanation:
Area of a Rectangle Formula: A = lw
Step 1: Write out expression:
l = 6w
w = w
Step 2: Plug in known variables
384 = 6w(w)
Step 3: Solve for w
385 = 6w²
w² = 64
w = 8
Step 4: Find l
l = 6(8)
l = 48
the length is 48
