Answers
Answer:
infinitely many solutions
Step-by-step explanation:
Related Questions
The areas of the bases of similar rectangular prisms are 25 square inches and 64 square inches.
What is the ratio of the volumes of the rectangular prisms?
5 to 8
15 to 24
75 to 192
125 to 512
Answers
Answer:
D. 125 to 512Step-by-step explanation:
The ratio of the areas of the bases:
25/ 64This is a square of the scale factor:
k² = 25/64The scale factor is:
k = √25/64 = 5/8The ratio of the volumes is the cube of the scale factor:
k³ = (5/8)³ = 125 / 512Correct choice is D
ratio of areas
25/64Ratio of sides
√25/645/8Ratio of volumes
(5/8)³125/512Option D
Solve the rational equation:
2x
x-3
2x-5
X-8x+15
-3
x-5*
==
A. x = 3, x = 5
B. There is no solution.
C. x = -3.09, x = 2.09
D. x = -0.41, x = 4.91
Answers
The solutions to the rational equation are; x = -0.41, 4.91.
Option B is the correct answer.
What are the solution of the rational equation?Given the rational equation in the question;
2x/x-3 - 2x-5/x²-8x+15 = -3/x-5
First, we factor the denominator x² - 8x + 15 using AC method
Replace x² - 8x + 15 with ( x - 5 )( x - 3 )
2x/x-3 - 2x-5/( x - 5 )( x - 3 ) = -3/x-5
Multiply each term in the equation by the LCD ( x - 5 )( x - 3 ) to eliminate the fractions
2x( x - 5 ) - (2x - 5) = -3( x - 3 )
Apply distributive property
2x² - 10x - 2x + 5 = -3x + 9
Add like terms
2x² - 12x + 5 = -3x + 9
2x² - 12x + 3x + 5 - 9 = 0
Add like terms
2x² - 9x - 4 = 0
Solve for x using the quadratic formula.
x = (-b±√(b² - 4ac)) / (2a)
a = 2,
b = -9
c = -4
x = (-(-9) ± √((-9)² - (4 × 2 × -4) )) / (2×2)
x = ( 9 ± √( 81 - (-32) )) / (4)
x = ( 9 ± √( 81 + 32 )) / (4)
x = ( 9 ± √( 113 ) ) / 4
x = ( 9 + √( 113 ) ) / 4, ( 9 - √( 113 ) ) / 4
x = 4.91, -0.41
To know more about the solution of the rational equation ,visit:
brainly.com/question/29148070
#SPJ1
Why is i squared equal to 1?
Answers
The square root of -1 is the definition of i. A square root is squared to eliminate the two and leave the original number.
Given that,
We have to find why i squared is equal to negative 1.
We know that,
The imaginary numbers are denoted as i.
We occasionally obtained negative integers in equations when using the radican (square root) symbol to solve them. When they realized this, some would halt and respond, "no actual solution," which is technically accurate. We can further simplify radicals by using the imaginary number I which is the square root of real numbers. We occasionally even manage to get rid of the fictitious element, which provides us with actual solutions.
The square root of -1 is the definition of i. A square root is squared to eliminate the two and leave the original number.
To learn more about square visit: https://brainly.com/question/29286039
#SPJ4
The proportion of children that catch a cold while at school is 0.49. As a school nurse explores options to help limit the spread of a virus in school, she sets up a study. For what sample size, n, will the sampling distribution of sample proportions have a standard deviation of 0.02? Provide your answer below:
children__
Answers
The sample size needed for the sampling distribution of sample proportions to have a standard deviation of 0.02 is approximately 628 children.
The formula for the standard deviation of the sampling distribution of sample proportions is:
\(σp = sqrt[p(1-p)/n]\)
Where p: population proportion (0.49 in this case) and n: sample size.
We are given that σp = 0.02. So, we can set up the equation:
\(0.02 = sqrt[0.49(1-0.49)/n]\)
Simplifying:
0.0004 = 0.24/n
n = 0.24/0.0004
n = 627.5 = 628
However, this is only an estimate because the sample size must be a whole number. Since we cannot have a fractional sample size, we round up to the nearest whole number:
n = 628
To calculate the sample size (n) needed to achieve a standard deviation of 0.02 for the sampling distribution of sample proportions, we'll use the formula:
\(Standard Deviation = sqrt[(P * (1 - P)) / n]\)
where P: proportion of children that catch a cold while at school (0.49), and n: sample size we want to find. We're given the desired standard deviation as 0.02. Now, let's solve for n:
\(0.02 = sqrt[(0.49 * (1 - 0.49)) / n]\)
Square both sides to get rid of the square root:
0.0004 = (0.49 * 0.51) / n
Now, solve for n:
n = (0.49 * 0.51) / 0.0004
n = 627.75
Since we can't have a fraction of a child, we'll round up to ensure the standard deviation is no greater than 0.02:
n = 628 children
Learn more about standard deviation here:
https://brainly.com/question/23907081
#SPJ11
10. A bank teller serves one customer in 5 minutes. Assuming the demand is 12 cust/hour, what is the utilization? A. 33.39 B. 50.0% C. 66.67% D. 100%
Answers
the utilization is approximately 1.67%, which is closest to option A. 33.39%.
Given:
- The bank teller serves one customer in 5 minutes.
- The demand is 12 customers per hour.
To find the average time per customer, we can invert the rate of serving customers per minute:
Average time per customer = 1 / (12 customers/hour 60 minutes/hour) = 1 / 720 customers/minute
Utilization is defined as the ratio of time spent serving customers to the total available time. Since the total available time is 60 minutes per hour, we can calculate the utilization as follows:
Utilization = (Time spent serving customers / Total available time) 100%
Time spent serving customers = Average time per customer Number of customers
Time spent serving customers = (1 / 720 customers/minute) (12 customers/hour)
Time spent serving customers = 12 / 720 hours
Utilization = (Time spent serving customers / Total available time) 100%
Utilization = (12 / 720 hours) / (1 hour) 100%
Utilization = 12 / 720 100%
Utilization = 1.67%
Therefore, the utilization is approximately 1.67%, which is closest to option A. 33.39%.
Learn more about Time Calculation here:
https://brainly.com/question/30895034
#SPJ11
Question 5 of 10
Which pair of functions are inverses of each other?
O A. f(x) = 2 + 15 and g(x) = 12x - 15
O B. f(x) = √3x and g(x) = () ³
O c. f(x) = 3 - 10 and g(x) = +10
3
D. f(x) = 11x-4 and g(x) = +4

Answers
The correct answer is D. f(x) = 11x - 4 and g(x) = (x + 4)/11
To determine which pair of functions are inverses of each other, we need to check if the composition of the functions results in the identity function, which is f(g(x)) = x and g(f(x)) = x.
Let's test each option:
Option A:
f(x) = x/2 + 15
g(x) = 12x - 15
f(g(x)) = (12x - 15)/2 + 15 = 6x - 7.5 + 15 = 6x + 7.5 ≠ x
g(f(x)) = 12(x/2 + 15) - 15 = 6x + 180 - 15 = 6x + 165 ≠ x
Option B:
f(x) = ∛3x
g(x) = (x/3)^3 = x^3/27
f(g(x)) = ∛3(x^3/27) = ∛(x^3/9) = x/∛9 ≠ x
g(f(x)) = (∛3x/3)^3 = (x/3)^3 = x^3/27 = x/27 ≠ x
Option C:
f(x) = 3/x - 10
g(x) = (x + 10)/3
f(g(x)) = 3/((x + 10)/3) - 10 = 9/(x + 10) - 10 = 9/(x + 10) - 10(x + 10)/(x + 10) = (9 - 10(x + 10))/(x + 10) ≠ x
g(f(x)) = (3/x - 10 + 10)/3 = 3/x ≠ x
Option D:
f(x) = 11x - 4
g(x) = (x + 4)/11
f(g(x)) = 11((x + 4)/11) - 4 = x + 4 - 4 = x ≠ x
g(f(x)) = ((11x - 4) + 4)/11 = 11x/11 = x
Based on the calculations, only Option D, where f(x) = 11x - 4 and g(x) = (x + 4)/11, satisfies the condition for being inverses of each other. Therefore, the correct answer is:
D. f(x) = 11x - 4 and g(x) = (x + 4)/11
for such more question on inverses
https://brainly.com/question/15066392
#SPJ8
The curve above is the graph of a sinusoidal function. It goes through the points (−4,−1) and (2,−1) . Find a sinusoidal function that matches the given graph. If needed, you can enter π=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits.
Answers
Given information: The curve above is the graph of a sinusoidal function. It goes through the points (−4,−1) and (2,−1) . We are to find a sinusoidal function that matches the given graph. So, the sinusoidal function that matches the given graph is y = sin [(π/3) (x - 4)] - 1.
The standard form of a sinusoidal function is given by y = a sin (bx - c) + d. Here, we have the two points: (-4, -1) and (2, -1). Since the y-coordinate is the same for both the points and it represents the amplitude, thus we have amplitude = 1
The x-coordinate of the midline of the sinusoidal function is the average of the x-coordinates of the two points and is given by(midline) = (−4 + 2)/2 = -1
The midline (horizontal line through the center of the sinusoidal function) is given by y = (midline) = -1
The distance between the two points is 6 units which represents the period (2π/b) of the sinusoidal function.
Thus, we have6 = (2π/b) => b = π/3We have the point (-4, -1), substituting it in the equation y = a sin (bx - c) + d-1 = a sin (b(-4) - c) + d...equation (1)
We have the point (2, -1), substituting it in the equation y = a sin (bx - c) + d-1 = a sin (b(2) - c) + d...equation (2)
We have two equations and two unknowns (a and c). By subtracting equation (1) from equation (2), we get0 = a(sin(2b - c) - sin(-4b - c))
The formula for difference of sines is given by2 sin [(A-B)/2] cos [(A+B)/2]
Applying the formula, we get 0 = 2a cos(5π/6 - c) sin(-3π/6 - c) => cos(5π/6 - c) = 0Since cos (5π/6) = -sqrt(3)/2, thus we have-c = 5π/6 + π/2 = 7π/6
Also, from equation (1), substituting c = 7π/6, we get-1 = a sin (-4b - 7π/6) + d
Since sin(-x) = -sin(x), thus we have-1 = -a sin (4b + 7π/6) + d => 1 = a sin (4b + 7π/6) - d
Now, we need to find the value of d. Since the midline is given by y = (midline) = -1
We have,1 = a sin (4b + 7π/6) + 1 => a sin (4b + 7π/6) = 0=> sin (4b + 7π/6) = 0 (since amplitude a is non-zero)=> 4b + 7π/6 = nπ, where n is an integer=> b = (nπ - 7π/6)/4
We have b = π/3, substituting this, we get nπ/4 - 7π/24 = π/3 => n = 3/2
Thus, we haven = nπ/4 - 7π/24 = (3π/2)/4 - 7π/24 = 5π/12
Substituting the values of a, b, c, and d, we have y = a sin (bx - c) + d= 1 sin (π/3 x - 7π/6) - 1 = sin [(π/3) (x - 4)] - 1. Hence, the sinusoidal function that matches the given graph is y = sin [(π/3) (x - 4)] - 1.
For more questions on: sinusoidal function
https://brainly.com/question/29529184
#SPJ8
Thirty students were surveyed about the number of siblings they have. Their results were recorded and placed on a card face down.
Outcome Frequency
1 6
2 12
3 9
4 or more 3
Determine P(2) when picking a random card.
40%
60%
70%
90%
Answers
Answer:40
Step-by-step explanation: 40 present
Answer:
90%
Step-by-step explanation:
8. A landowner digs a 15-meter-deep well with a diameter of 2.8 meters. The landowner spreads the dirt dug out of the hole to form a flat platform 31.5 meters by 6 meters. Find the height in centimeters of the platform. Enter your answer in centimeters rounded to the nearest tenth.
Answers
The height in centimeters of the platform is 48.9 centimeters.
To find the height in of the platform formed by spreading the dirt dug out of a well is;
Step 1: Calculate the volume of the well.
The well is in the shape of a cylinder, so we can use the formula for the volume of a cylinder: V = πr^2h, where V is the volume, r is the radius, and h is the height (depth in this case). The diameter is 2.8 meters, so the radius is half of that, which is 1.4 meters.
V = π(1.4^2)(15)
V ≈ 92.4 m^3
Step 2: Calculate the volume of the platform.
Since the volume of the dirt in the well is equal to the volume of the dirt used to form the platform, we can set up an equation to find the height (h) of the platform.
Volume of the platform = Length x Width x Height
92.4 = 31.5 x 6 x h
Step 3: Solve for the height (h).
92.4 = 189h
h ≈ 0.489 meters
Step 4: Convert the height to centimeters and round to the nearest tenth.
0.489 meters = 48.9 centimeters
So, the height of the platform is approximately 48.9 centimeters.
Know more about height here:
https://brainly.com/question/12446886
#SPJ11
SQUARE ROOT OF 21316 WITH STEP BY STEP SOLUTION THANKS
Answers
Answer:
146
Step-by-step explanation:
\( = \sqrt{21316 } \)
\( = \sqrt{4 \times 5329} \)
\( = 2 \sqrt{5329} \)
\( = 2 \sqrt{73 \times 73} \)
\( = 2 \times 73\)
\( = 146\)
Which one of the following is a function?
O4x - 2y² = 9
O4x² - 2y² = 9
O4x - 2y = 9
Answers
Write a story that can be represented using the equation y=x+1/5x
Answers
A story that can be represented using the equation y=x+1/5x is "John has an apple and he cut another apple into 5 equal parts and took on part. What's the rural fraction of apple that he has?
How to illustrate the equation?An equation is the statement that illustrates the variables given. In this case, two or more components are taken into consideration to describe the scenario. It is vital to note that an equation is a mathematical statement which is made up of two expressions that are connected by an equal sign.
In this case, if John has an apple and he cut another apple into 5 equal parts and took on part.
This can be illustrated as:
y = x + 1/5x
Learn more about equations on:
brainly.com/question/2972832
#SPJ1
Please help, I only have 1 attempt left to get it right, there is also no need to show your work if you don't want to.
How many pounds of $1.75/lb trail mix should a grocer combine with 3 lb of $3.75/lb trail mix to get $2.95/lb trail mix?
Answers
Answer:
1/2 lb
Step-by-step explanation:
(1)1.75 + 3(3.75) - 4 = 23.5/4
23.5x/4 = 2.95
23.5x = 11.8
x = 0.5
Answer:
2lb
I don't know what to write here but this is the answer
a bus drives for 3 and a half hours at an average speed of 56mph how far does the bus drive?
Answers
Answer:
196 miles
Step-by-step explanation:
distance (D) is calculated as
D = S × T ( S is average speed and T is time in hours )
here T = 3 and a half hours = 3.5 hours and S = 56 , then
D = 56 × 3.5 = 196 miles
Consider the parabola y = 2(x − 1)^2 + k. Find the value of k if the y-intercept is 8
Answers
Answer:
6
Step-by-step explanation:
if y-intercept is 8, means when x = 0, y = 8
8 = 2(− 1)^2 + k
8 = 2 + k
k = 6
Martina has 16 cars available to rent. let c be the number of cars she would have left after renting r of them. write an equation relating c to r. then use this equation to find the number of cars she would have left after renting 14 of them.
Answers
If Martina has 16 cars available to rent, and if c is the number of cars she would have left after renting r of them, then the equation relating c to r will be c = 16 - r, and the number of cars she would have been left with after renting 14 of them is calculated to be 2.
An algebraic expression is a type of expression consisting of both numerals and letters.
If Martina has a total of 16 cars available to rent, then the equation or algebraic expression relating c to r is,
c = total number of cars available to rent - r
c = 16 - r
After renting 14 of the total cars available, then the number of cars left can be calculated using this equation,
c = 16 - r
c = 16 - 14
c = 2
Thus, the number of cars she would have been left with is calculated to be 2.
To learn more about algebraic expressions, click here:
https://brainly.com/question/4344214
#SPJ4
a quantity of interest that can take on different values is known as a(n)
Answers
a quantity of interest that can take on different values is known as a(n)
variable.
To know more about variable refer here:
https://brainly.com/question/17344045
#SPJ11
What is the image of (12,-12) after a dilation by a scale factor of 1/3 centered at the origin?
Answers
The image of (12,-12) after a dilation by a scale factor of 1/3 centered at the origin is (4, -4).
What is dilation at origin?
On the coordinate plane, figures can be magnified. The centre of dilation is frequently the origin. The coordinates of the points in the preimage can be multiplied by the scale factor to get the points in the image if you are distorting a figure that is centered at the origin.
We have to find the image of (12,-12) after a dilation by a scale factor of 1/3 centered at the origin.
To find the image after dilation multiply both coordinates (12, -12) by 1/3 which is the same as dividing by 3.
⇒ (12, -12)*1/3 = (4, -4)
Hence, the image of (12,-12) after a dilation by a scale factor of 1/3 centered at the origin is (4, -4).
To know more about dilation, click on the link
https://brainly.com/question/17403117
#SPJ1
K(x)=12(1+1)^x,k(3)
Show how you got the answer step by step
Answers
Find the measure of the indicated angle to the nearest degree.
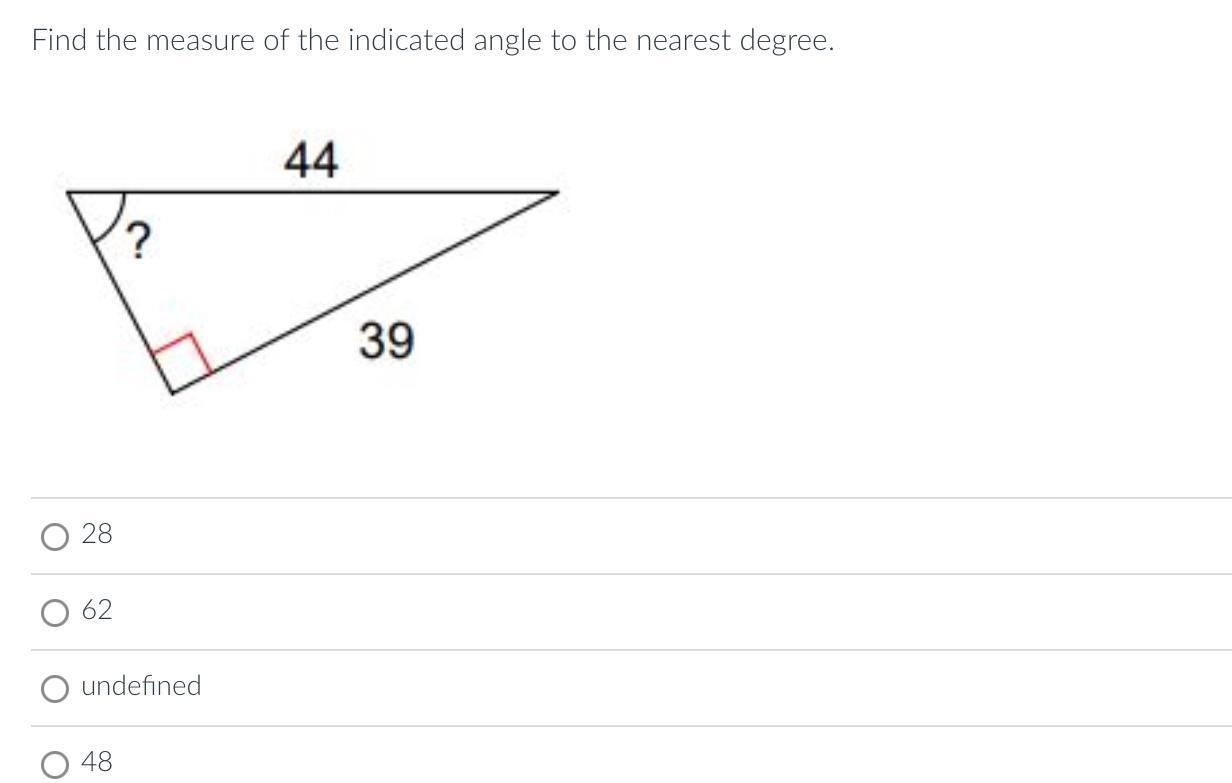
Answers
Answer:
62°
Step-by-step explanation:
We use the fact that the ratio of the sides of the triangle to the angles opposite them is given by the Law of Sines:
"In any triangle, the ratio of a side length to the sine of its opposite angle
is the same for all three sides"
\(\frac{a}{sinA} = \frac{b}{sinb} =\frac{c}{sinC}\)
where A is the is the angle opposite side a, B the angle opposite to side b, C is the angle opposite to side c
For the given triangle we get
44/sin90 = 39/sin?
sin90 is 1 so we get 44/1 = 39/sin?
or cross-multiplying,
sin? = 39/44 = 0.886363..
? = sin⁻¹ (0.886363) = 62.42° ≈ 62° answer
Answer:
? ≈ 62°
Step-by-step explanation:
using the sine ratio in the right triangle
sin? = \(\frac{opposite}{hypotenuse}\) = \(\frac{39}{44}\) , then
? = \(sin^{-1}\) ( \(\frac{39}{44}\) ) ≈ 62° ( to the nearest degree )
Ayuden por favor, no entiendo este problema

Answers
We will get that the angle theta is:
θ = β/2
How to find the value of theta?Remember that the sum of the interior angles of any triangle must be equal to 180°.
Now, looking at the triangle in the left, we can see that the top angle is equal to:
180 - 2α
The right angle is equal to:
180 - 2β
And the left angle is α
Then we can write:
α + (180 - 2α) + (180 - 2β) = 180
-α - 2β = -180
α = 180 - 2β
Now we can go to the other triangle, where theta is, and write:
α + β + 2θ = 180
Replacing what we found above, we get:
180 - 2β + β + 2θ = 180
-β + 2θ = 0
θ = β/2
That is the best simplification we can get with the given diagram.
Learn more about interior angles at:
https://brainly.com/question/24966296
#SPJ1
Is 0. 19
a rational or irrational? Explain
Answers
Answer:
It's rational, because it can be converted into a reasonable fraction.
➯ Hope this helps!
the probability that an observation taken from a standard normal population will have a z value less than 0.5 and greater than ‒1.5, i.e., p(‒1.5
Answers
The probability that an observation taken from a standard normal population will have a z-value less than 0.5 and greater than -1.5, i.e., P(-1.5 < Z < 0.5), is approximately 0.6247.
Determine the probability.
To find the probability P(-1.5 < Z < 0.5), where Z represents a standard normal random variable, we can use the standard normal distribution table or statistical software.
The standard normal distribution table provides the cumulative probabilities for various values of Z. By looking up the probabilities for -1.5 and 0.5 individually and subtracting them, we can find the desired probability.
Alternatively, using statistical software or a calculator, we can calculate the probability directly by subtracting the cumulative probability of -1.5 from the cumulative probability of 0.5.
In this case, the probability P(-1.5 < Z < 0.5)
P(-1.5 < z < 0.5) = P(z < 0.5) - P(z < -1.5)
= 0.6915 - 0.0668
= 0.6247
This means that there is a 0.6247, or 62.47%.chance of obtaining a Z-value between -1.5 and 0.5 in a standard normal distribution.
To know more about probability, refer here:
https://brainly.com/question/29381779#
#SPJ4
There are 5 Kit Kats and 4 Snickers in a bag. If there are 24 snickers, how many Kit Kats are there?
Answers
Answer: 30 Kit Kats
Step-by-step explanation:
The ratio of Kit Kats to Snickers is 5:4 or \(\frac{5}{4}\)
Let us name Kit Kats as "k", if there are 24 Snickers:
we need to find the number of Kit Kats that keeps ratio constant
\(\frac{5}{4} = \frac{k}{24}\) ... crossmultiply
5 * 24 = 4 * k
120 = 4k
k = 30
The tax rate increased from 25% to 40%.a. What is the absolute change in percentage points? b. What is the relative change?
Answers
Answer:
a. 15%
b. 60%
Explanation:
Part a.
The absolute change in percentage points can be calculated as
\(\text{ Absolute change = Final value - Initial value}\)So, by replacing the final value with 40% and the initial value with 25%, we get
\(\text{ Absolute change = 40\%-25\% = 15\%}\)Therefore, the absolute change is 15%
Part b.
The relative change can be calculated as
\(\text{ Relative change = }\frac{\text{ Final value - Initial Value}}{\text{ Initial value}}\times100\)Replacing the final value with 40% and the initial value with 25%, we get
\(\begin{gathered} \text{ Relative change = }\frac{\text{ 40\% - 25\%}}{\text{ 25\%}}\times100 \\ \\ \text{ Relative change =}\frac{\text{ 15\%}}{\text{ 25\%}}\times100 \\ \\ \text{ Relative change = 0.6}\times100 \\ \text{ Relative change = 60\%} \end{gathered}\)Therefore, the relative change is 60%
An inscribed angle is an angle whose vertex is a point on a circle and whose sides are two _____ of the circle
Answers
An inscribed angle is formed by two chords of a circle that intersect at a vertex located on the circle.
The angle itself is formed by the two sides of the angle, which are the line segments connecting the vertex to the endpoints of the chords. The property that makes inscribed angles interesting is that the measure of an inscribed angle is half the measure of the intercepted arc on the circle.
This relationship holds true for any inscribed angle in a circle, making it a useful concept in geometry for solving problems involving angles, arcs, and circles.
To know more about geometry visit-
brainly.com/question/30283669
#SPJ11
Which graph repreWhich value can fill in the blank in the function f(x) = ____|x| to make its graph wider than that of the parent function, f(x) = |x|?
–1
1
4sents the function f(x) = |x| – 4?
Answers
Answer:
the answer is -1
Step-by-step explanation:
I took the quiz
Triangle ABC is dilated by a scale factor of 2 with a center of dilation at the origin to create A'B'C'. What are the coordinates of the verticles of A'B'C'? EXPLAIN HOW YOU GOT THE ANSWER, Please help I will mark you brainliest.

Answers
The coordinates of A'B'C' are given as follows:
D. A'(4,4), B'(8,8), C'(-8,4).
What is a dilation?A dilation happens when the coordinates of the vertices of an image are multiplied by the scale factor, changing the side lengths of a figure.
The coordinates of the original triangle ABC are given as follows:
A(2,2), B(4,4), C(-4,2).
The scale factor for the dilation is given as follows:
k = 2.
Hence the coordinates of A'B'C' are obtained multiplying the coordinates of ABC by the scale factor of two, as follows:
A'(4,4), B'(8,8), C'(-8,4).
More can be learned about dilation at brainly.com/question/3457976
#SPJ1
in a certain country, the car number plate is formed by 4 digits from the digits 1, 2, 3, 4, 5, 6, 7, 8 and 9 followed by 3 letters from the alphabet. how many number plates can be formed if neither the digits nor the letters are repeated? show the necessary steps.
Answers
The license plates can be formed if neither the digits nor the letters are repeated is 78,624,000 , this can be calculated by using permutation and combination.
What are permutation and combination?
A permutation is an act of arranging the objects or elements in order. Combinations are the way of selecting objects or elements from a group of objects or collections, in such a way the order of the objects does not matter.
Main Body:
In a certain country, the car license plate is formed by 4 numbers from the digits 1-9 followed by 3 letters from the alphabet.
There are 10 numbers.
And there is 26 alphabet.
The license plates can be formed if neither the digits nor the letters are repeated will be
⇒(numbers) (alphabet)
⇒ (9*8*7*6)(26*25*24)
⇒ 78,624,000
Hence, The license plates can be formed if neither the digits nor the letters are repeated is 78,624,000.
More about the permutation and the combination link is given below.
https://brainly.com/question/11732255
#SPJ4
Two less than the quotient of a number and 8 is 1/4.Find the number
Answers
For the given problem:
Let the number = x
Two less than the quotient of a number and 8 is 1/4
so, we can write the following expression:
\(\frac{x}{8}-2=\frac{1}{4}\)Now, solve the equation to find (x)
Multiplying by (8) to eliminate the denominators:
\(\begin{gathered} 8\cdot(\frac{x}{8}-2)=8\cdot\frac{1}{4} \\ \\ 8\cdot\frac{x}{8}-8\cdot2=\frac{8}{4} \\ x-16=2 \end{gathered}\)Add (6) to both sides:
\(\begin{gathered} x-16+16=2+16 \\ x=18 \end{gathered}\)So, the answer will be the number is 18
