What the next pattern of A, C, E, G, I

The last one. Indeed : the couple (x,y) = (-3,2)

Lets replace the values :

2*(-3) + 4*2 = 2

-6 + 8 - 2 = -8 + 8 = 0

And -2*(-3) + 2*2 = 10

6+4 -10 = 10-10 = 0

Good Luck

The point (-3, 2) is a solution to the pair of equations: 2x + 4y = 2 and -2x + 2y = 10. Option D

We know that the solution would yield the value at the RHS when we substitute it thus we have that;

Substituting x = -3 and y = 2 into the first equation:

2(-3) + 4(2) = -6 + 8 = 2 (Satisfied)

Substituting x = -3 and y = 2 into the second equation:

-2(-3) + 2(2) = 6 + 4 = 10 (Not satisfied)

Since the point (-3, 2) satisfies the first equation, but not the second, it is not a solution to this pair of equations.

Learn more about simultaneous equation:https://brainly.com/question/20627346

#SPJ3

9514 1404 393

Answer:

  n^2 +n +4

Step-by-step explanation:

Since the divisor has only one term, the quotient is formed by dividing the terms one at a time.

  \(\dfrac{4n^4+4n^3+16n^2}{4n^2}=\dfrac{4n^4}{4n^2}+\dfrac{4n^3}{4n^2}+\dfrac{16n^2}{4n^2}=\boxed{n^2 +n +4}\)

__

Your long division tableau will subtract n^2×4n^2 = 4n^4 to form the new dividend 4n^3+16n^2. Then you will subtract n×4n^2 = 4n^3 to get the new dividend of 16n^2. The final quotient term is 4, and you will subtract 4×4n^2 to get a remainder of 0. You will have written the quotient as n^2+n+4.

The Trigonometric Expression can be written as  :

cos⁴ x = 18(3 + 4cos2x + cos4x)

Power:

In mathematics, a power defines a base number raised to an exponent. The base is the factor multiplied by itself, and the exponent is the number of times the same base is multiplied.

Reducing / Lowering Power:

Power identities are trigonometric identities, allowing us to rewrite trigonometric expressions raised to powers in terms of simpler trigonometric expressions.

According to the question:

cos2x = 2cos²x -1

⇒ cos²x = 1/2 (1 + cos2x)

⇒ cos²2x = 1/2 (1 + cos4x)

⇒ cos⁴ x = (cos²x)²  

          = 1/4(1 + 2cos2x+cos²2x)

⇒ cos⁴ x = 1/4( 1 + 2cos2x + 1/2(1+cos4x))

⇒ cos4x = 1/8(3 + 4cos2x+cos4x)

Learn more about Trigonometric Expression:

https://brainly.com/question/11659262

#SPJ4

Answer:

Can you put the answer?

Step-by-step explanation:

well, he has left only 6 oz.

now, if we take the 16(origin amount) to be the 100%, what is 6 off of it in percentage?

\(\begin{array}{ccll} amount&\%\\ \cline{1-2} 16 & 100\\ 6& x \end{array} \implies \cfrac{16}{6}~~=~~\cfrac{100}{x} \\\\\\ \cfrac{ 8 }{ 3 } ~~=~~ \cfrac{ 100 }{ x }\implies 8x=300\implies x=\cfrac{300}{8}\implies x=\cfrac{75}{2}\implies x=37.5\)

Answer:

-6

Step-by-step explanation:

-1(3) + 1 / 4(3)

-3+1/12

-2/12 = -6

if that's what you mean

Answer:

There are 3 lie detectors each of which accurate 70% of time what is the

Step-by-step explanation:

There are 3 lie detectors each of which accurate 70% of time what is the combined accuracy of the three lie detectors put together? (In the case where two lie detector predict one result and the third predicts an opposite result the result of the two detector giving same result will be considered )

Answer:

-----------------------------

Given function:

Graph it first (see attached).

Test the graph for symmetry.

We know the odd degree parent function y = x³ has an origin symmetry, whilst even degree functions may have axis symmetry.

The given function is a translation of cubic function 5 units up so the center of symmetry has translated as well. Therefore correct answer is 4.

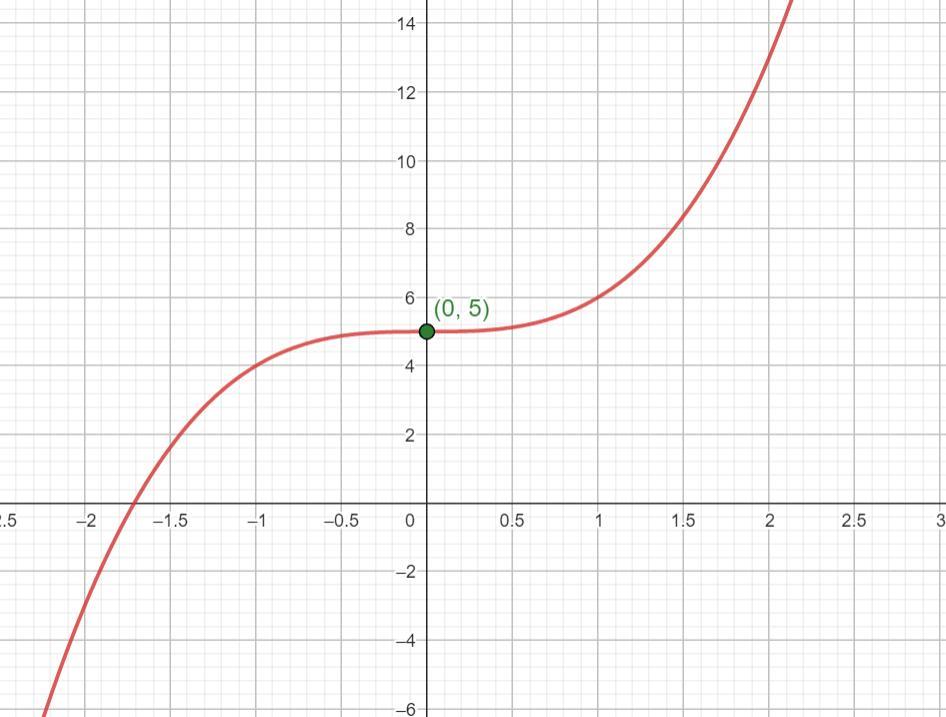
Answer:

4. no origin symmetry

Step-by-step explanation:

Functions are symmetric with respect to the x-axis if for every point (a, b) on the graph, there is also a point (a, −b) on the graph:

To determine if a graph is symmetric with respect to the x-axis, replace all the y's with (−y).  If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the x-axis.

\(\begin{aligned}&\textsf{Given}: \quad &y &= x^3 + 5\\&\textsf{Replace $y$ for $(-y)$}: \quad &-y &= x^3 + 5\\&\textsf{Simplify}: \quad &y &= -x^3 - 5\end{aligned}\)

Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the x-axis.

--------------------------------------------------------------------------------------------------

Functions are symmetric with respect to the y-axis if for every point (a, b) on the graph, there is also a point (-a, b) on the graph:

To determine if a graph is symmetric with respect to the x-axis, replace all the x's with (−x).  If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the y-axis.

\(\begin{aligned}&\textsf{Given}: \quad &y&=x^3+5\\&\textsf{Replace $x$ for $(-x)$}: \quad &y&=(-x)^3+5\\&\textsf{Simplify}: \quad &y&=-x^3+5\end{aligned}\)

Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the y-axis.

--------------------------------------------------------------------------------------------------

Functions are symmetric with respect to the origin if for every point (a, b) on the graph, there is also a point (-a, -b) on the graph:

To determine if a graph is symmetric with respect to the origin, replace all the x's with (−x) and all the y's with (-y).  If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the origin.

\(\begin{aligned}&\textsf{Given}: \quad &y&=x^3+5\\&\textsf{Replace $x$ for $(-x)$ and $y$ for $(-y)$}: \quad &(-y)&=(-x)^3+5\\&\textsf{Simplify}: \quad &-y&=-x^3+5\\&&y&=x^3-5\end{aligned}\)

Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the origin.

Answer:

\(2x + 3x = 180 \\ because \: they \: are \: o n \: one \: line \\ 5x = 180 \\ x = 180 \div 5 = 36\)

a) There are 2400 animals on the farm.

b) The number of sheep on the farm is 700.

c) The percentage of rabbits in relation to the total number of animals is 37.5%.

d) The angle that represents the number of pigs is 75 degrees.

a) To determine the total number of animals on the farm, we add up the number of rabbits, sheep, cattle, and pigs:

Total number of animals = 900 (rabbits) + 700 (sheep) + 300 (cattle) + 500 (pigs) = 2400 animals.

b) The number of sheep on the farm is given as 700.

c) To calculate the percentage of rabbits in relation to the total number of animals, we divide the number of rabbits by the total number of animals and multiply by 100:

Percentage of rabbits = (900 / 2400) * 100 = 37.5%.

d) To calculate the angle that represents the number of pigs, we need to find the proportion of the total number of animals that pigs make up, and then convert it to an angle on the pie chart.

Proportion of pigs = 500 / 2400 = 0.2083.

To find the angle in degrees, we multiply the proportion by 360 degrees:

Angle representing pigs = 0.2083 * 360 = 75 degrees.

for such more question on percentage

https://brainly.com/question/24877689

#SPJ8

right

L shaped angles are right angles

Acute angles are angles below 90 degrees, so think of a really skinny V shape

Obtuse angles are over 90 degrees, so wider than an L

Answer:D

Step-by-step explanation:

Answer:

28

Step-by-step explanation:

28/2=14

28/4=7

28/7=4

28 is an even number

Step-by-step explanation:

28 is the answer

28 is a number between 20 and 30

and divisible by

28/2=14

28/4=7

28/7=4

Answer:

Solve for x, y, and z. 1st Equation: 2x + 2y + 4z = 48. 2nd Equation: 2x + 9y + 7z = 105. 3rd Equation: x + 4y + z = 37. Subtract the 2nd Equation from the 1st Equation. This will eliminate the variable “x”.

Step-by-step explanation:

Answer:

Step-by-step explanation:

A, B, E

Given statement solution is :- It  would cost $680 to install tile in the dining room and $315 to install carpet in the bedroom.

To find the cost of installing tile in the dining room and carpet in the bedroom, we need to calculate the areas of both rooms first.

Given:

Every 2 centimeters on the floor plan represents 1 meter of the house.

Dining Room:

On the floor plan, the dining room is 8 cm by 10 cm.

Converting this to meters, the dimensions of the dining room are 8 cm / 2 = 4 meters by 10 cm / 2 = 5 meters.

The area of the dining room is 4 meters * 5 meters = 20 square meters.

Bedroom:

On the floor plan, the bedroom is 6 cm by 10 cm.

Converting this to meters, the dimensions of the bedroom are 6 cm / 2 = 3 meters by 10 cm / 2 = 5 meters.

The area of the bedroom is 3 meters * 5 meters = 15 square meters.

Now, let's calculate the costs.

Cost of Tile:

The cost of installing tile is $34 per square meter.

The area of the dining room is 20 square meters.

Therefore, the cost of installing tile in the dining room is 20 square meters * $34/square meter = $680.

Cost of Carpet:

The cost of installing carpet is $21 per square meter.

The area of the bedroom is 15 square meters.

Therefore, the cost of installing carpet in the bedroom is 15 square meters * $21/square meter = $315.

Therefore, it would cost $680 to install tile in the dining room and $315 to install carpet in the bedroom.

For such more questions on Cost of tile and carpet.

https://brainly.com/question/29574063

#SPJ8

When a mass of 3 kg is hanged to it, the string will stretch 7.5 cm.

Given,

The length of the spring attached to the ceiling = 10 cm

The quantity of the mass hanged in the spring = 2 kg

The amount of stretching happened in the spring = 15 cm

We have to find the stretching of string when a mass of 3 kg is hanged to it;

Here,

Given that the force applied to the spring by the 2.0 kg is equal to the mass's weight:

F = mg = 2 kg × 9.8 m/s² = 19.6 N

Additionally, the stretching of:

Δx = 15 cm - 10 cm = 5 cm

So, applying Hooke's law:

F = kΔx

To determine the spring constant, k;

k = F/Δx = 19.6/5 = 3.92  N/ cm

The spring is now coupled to a new mass of m = 3.0 kg; the force this mass exerts on the spring equals

F = mg = 3 kg × 9.8 m/s² = 29.4 N

Thus, we may apply Hooke's law once more to determine the new stretching:

Δx = F/k = 29.4/3.92 = 7.5 cm

Therefore,

The string will be stretched 7.5 cm when a mass of 3 kg is hanged to it.

Learn more about stretching of string here;

https://brainly.com/question/12803029

#SPJ4

We know that:

Then:

Therefore:

Simplifying the above result we get:

Answer:

Answer:

35 degrees is the third angle's value.

Based on the given assumptions and calculations, the net present value (NPV) of the investment in the new piece of equipment is -$27,045.76, indicating that the investment is not favorable.

To calculate the after-tax cash flows for each year and evaluate the investment decision, let's use the following information:

Assumptions:

Tax depreciation is straight-line over five years.

Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4.

Tax on salvage value is 30% of the difference between salvage value and book value of the investment.

The cost of capital is 12%.

Given:

Initial investment cost = $50,000

Useful life of the equipment = 5 years

To calculate the depreciation expense each year, we divide the initial investment by the useful life:

Depreciation expense per year = Initial investment / Useful life

Depreciation expense per year = $50,000 / 5 = $10,000

Now, let's calculate the book value at the end of each year:

Year 1:

Book value = Initial investment - Depreciation expense per year

Book value \(= $50,000 - $10,000 = $40,000\)

Year 2:

Book value = Initial investment - (2 \(\times\) Depreciation expense per year)

Book value \(= $50,000 - (2 \times$10,000) = $30,000\)

Year 3:

Book value = Initial investment - (3 \(\times\) Depreciation expense per year)

Book value = $50,000 - (3 \(\times\) $10,000) = $20,000

Year 4:

Book value = Initial investment - (4 \(\times\) Depreciation expense per year)

Book value \(= $50,000 - (4 \times $10,000) = $10,000\)

Year 5:

Book value = Initial investment - (5 \(\times\) Depreciation expense per year)

Book value \(= $50,000 - (5 \times $10,000) = $0\)

Based on the assumptions, the salvage value is $10,000 in Year 5.

If the asset is scrapped in Year 4, the salvage value is $15,000.

To calculate the tax on salvage value, we need to find the difference between the salvage value and the book value and then multiply it by the tax rate:

Tax on salvage value = Tax rate \(\times\) (Salvage value - Book value)

For Year 5:

Tax on salvage value\(= 0.30 \times ($10,000 - $0) = $3,000\)

For Year 4 (if scrapped):

Tax on salvage value\(= 0.30 \times ($15,000 - $10,000) = $1,500\)

Now, let's calculate the after-tax cash flows for each year:

Year 1:

After-tax cash flow = Depreciation expense per year - Tax on salvage value

After-tax cash flow = $10,000 - $0 = $10,000

Year 2:

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $0 - $0 = $0

Year 3:

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $0 - $0 = $0

Year 4 (if scrapped):

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $15,000 - $1,500 = $13,500

Year 5:

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $10,000 - $3,000 = $7,000

Now, let's calculate the net present value (NPV) using the cost of capital of 12%.

We will discount each year's after-tax cash flow to its present value using the formula:

\(PV = CF / (1 + r)^t\)

Where:

PV = Present value

CF = Cash flow

r = Discount rate (cost of capital)

t = Time period (year)

NPV = PV Year 1 + PV Year 2 + PV Year 3 + PV Year 4 + PV Year 5 - Initial investment

Let's calculate the NPV:

PV Year 1 \(= $10,000 / (1 + 0.12)^1 = $8,928.57\)

PV Year 2 \(= $0 / (1 + 0.12)^2 = $0\)

PV Year 3 \(= $0 / (1 + 0.12)^3 = $0\)

PV Year 4 \(= $13,500 / (1 + 0.12)^4 = $9,551.28\)

PV Year 5 \(= $7,000 / (1 + 0.12)^5 = $4,474.39\)

NPV = $8,928.57 + $0 + $0 + $9,551.28 + $4,474.39 - $50,000

NPV = $22,954.24 - $50,000

NPV = -$27,045.76

The NPV is negative, which means that based on the given assumptions and cost of capital, the investment in the new piece of equipment would result in a net loss.

Therefore, the investment may not be favorable.

Please note that the calculations above are based on the given assumptions, and additional factors or considerations specific to the business should also be taken into account when making investment decisions.

For similar questions on assumptions.

https://brainly.com/question/15424356  

#SPJ8

The complete question may be like :

Assumptions: Tax depreciation is straight-line over five years. Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4. Tax on salvage value is 30% of the difference between salvage value and book value of the investment. The cost of capital is 12%.

You are evaluating an investment in a new piece of equipment for your business. The initial investment cost is $50,000. The equipment is expected to have a useful life of five years.

Using the given assumptions, calculate the after-tax cash flows for each year and evaluate the investment decision by calculating the net present value (NPV) using the cost of capital of 12%.

Answer:

The average rate of change = 4

Step-by-step explanation:

Given the function

\(f\left(x\right)\:=\:2x^2\:-\:4\)

x₁=-2, x₂=4

f(x₁) = f(-2) = 2x²-4 = 2(-2)²-4 = 8-4 = 4

f(x₂) = f(4) = 2x²-4 = 2(4)²-4 = 32-4 = 28

The average rate of change = f(x₂) - f(x₁) / x₂ - x₁

                                                = (28-4)/(4-(-2))

                                                = 24/6

                                                = 4

Thus, the average rate of change = 4

Answers:

==========================================================

Explanation:

For the theoretical probability, we ignore the table completely. We just consider that each card has an equal chance of showing up. We have 5 cards total (1 through 5), and exactly one card shows the value "4". The theoretical probability of picking this card is 1/5 = 0.20 = 20%

Now we'll consider the table when it comes to computing the experimental probability (aka empirical probability). The table says that the card labeled "4" shows up exactly 48 times out of 200 total. Therefore, we get an experimental probability of 48/200 = 0.24 = 24%

We see that the theoretical probability is less than the experimental probability. If we did more trials (eg: say 1000 trials instead of 200), then the experimental probability should get closer to 20% based on the law of large numbers. The theoretical probability will stay the same no matter how many trials you do. In a sense, the theoretical probability is the target we aim for while the experimental probability is where we actually land on the dart board.

The expected total dollar net operating Income for next year = $70,000

1) The contribution format income statement for the game last year, and the degree of operating leverage is computed below:

Contribution format income statement for the game last year Sales (15,000 × $20) = $300,000

Variable expenses (15,000 × $6) = $90,000

Contribution margin = $210,000

Fixed expenses = $182,000Net operating income = $28,000

Degree of operating leverage = Contribution margin / Net operating income= $210,000 / $28,000= 7.5 2)

The expected percentage increase in net operating income for next year:

The expected sales in next year = 18,000

games selling price per game = $20

Therefore, Total sales revenue = 18,000 × $20 = $360,000

Variable expenses = 18,000 × $6 = $108,000

Fixed expenses = $182,000

Expected net operating income = Total sales revenue – Variable expenses – Fixed expenses

= $360,000 – $108,000 – $182,000= $70,000

The expected percentage increase in net operating income = (Expected net operating income - Last year's net operating income) / Last year's net operating income*100= ($70,000 - $28,000) / $28,000*100= 150%

The expected total dollar net operating income for next year = $70,000

To know more about Income.

https://brainly.com/question/30467914

#SPJ8

Answer:

\(4fg^{2}\)

Step-by-step explanation:

1) Remove parentheses.

\(fg^{2} *4\)

2) Regroup terms.

\(4fg^{2}\)

Answer:

The correct answer is...

Step-by-step explanation:

"F^4g^8" Hope this helps!

Answer:

Raspberry: 30%

Strawberry: 15%

Apple: 20%

Lemon: 35%

Step-by-step explanation:

18 + 9 + 12 + 21 = 60 (there are 60 gummy worms)

18 out of 60 = 30%

9 out of 60 = 15%

12 out of 60 = 20%

21 out of 60 = 35%

Please mark Brainliest

Hope this helps

Answer:

Raspberry Worms: 30%

Strawberry Worms: 15%

Apple Worms: 20%

Lemon Worms: 35%

Step-by-step explanation:

Raspberry Worms: \(\frac{18}{18+9+12+21}=\frac{18}{60}=\frac{30}{100}\) or 30%

Strawberry Worms: \(\frac{9}{18+9+12+21}=\frac{9}{60} =\frac{15}{100}\) or 15%

Apple Worms: \(\frac{12}{18+9+12+21} =\frac{12}{60} =\frac{20}{100}\) or 20%

Lemon Worms: \(\frac{21}{18+9+12+21} =\frac{21}{60} =\frac{35}{100}\) or 35%

Answer:

Yes

Step-by-step explanation:

8 + y = 4x is a linear equation in two variables ( x and y) .

Answer:

0.05

Step-by-step explanation:

In the given right triangle,

BC=5

AC=12.

Hypotenuse of the triangle, AB=13.

Now, the ratio of sin A can be expressed as,

The opposite side to angle A is BC.

Hence,

The ratio of cos A can be expresssed as,

The side adjacent to angle A is AC.

Hence,

The ratio tan A can be expressed as,

Therefore, sin A=5/13, cos A=12/13 and tan A=5/12.

First it helps to list out the multiples of 474

When computing 7÷474, we'll have 7 under the division bar when it comes to the long division process. Treat the 7 underneath the bar as 7.0 and think of it like the number 70

Now ask yourself how many times does 474 go into 70? The answer is "0 times". So we'll have 0.0 so far in the quotient above the bar.

Then ask "how many times does 474 go into 700?" The answer would be 1 time based on the list of multiples I showed above. We have 474*1 = 474 smaller than 700. The next multiple 474*2 = 948 is too big.

The next digit in the quotient decimal value is 1, so we have 0.01 so far.

That digit 1 multiplies with 474 to get 474 under the 7.00

Check out the diagram below to see what I mean. Then 700-474 = 226 and then we pull down a zero to get 2260, and restart the cycle over again. This process repeats indefinitely depending how many decimal digits you want in the final answer.

7÷474 = 0.014769 approximately