what is the square root of 139?
Answers
the square root of 139 is 11.78
Related Questions
Mary would like to join the track team. At the end of the first week of practice, Mary could run a lap in 2 minutes and 5 seconds. At the end of the second week of practice, Mary could run a lap in 1 minute and 58 seconds. After another week of practice, Mary could run a lap in 1 minute and 51 seconds. Mary continued to practice.
Answers
Answer:
1 minute and 44 seconds... 1 minute and 37 seconds. a pattern of -7 seconds
ryosuke is picking up his friend from work. the odometer reads $74,568$ when he picks his friend up, and it reads $74,592$ when he drops his friend off at his house. ryosuke's car gets $28$ miles per gallon and the price of one gallon of gas is $\$4.05$. what was the cost of the gas that was used for ryosuke to drive his friend back home from work? (express your answer in dollars and round to the nearest cent.)
Answers
To calculate the cost of the gas used by Ryosuke to drive his friend back home from work, we need to determine the distance traveled and then calculate the corresponding fuel consumption and cost.
Given that the odometer reading increased from 74,568 to 74,592, and the car gets 28 miles per gallon, we can calculate the distance traveled as 24 miles. Multiplying the distance by the fuel consumption rate, we find that Ryosuke used approximately 0.857 gallons of gas. Multiplying this by the price of one gallon ($4.05), we determine that the cost of the gas used is approximately $3.47.
To calculate the distance traveled by Ryosuke, we subtract the initial odometer reading from the final odometer reading: 74,592 - 74,568 = 24 miles.
Since Ryosuke's car gets 28 miles per gallon, we can determine the fuel consumption by dividing the distance traveled by the fuel efficiency: 24 miles / 28 miles per gallon = 0.857 gallons.
To calculate the cost of the gas used, we multiply the fuel consumption by the price per gallon: 0.857 gallons * $4.05 per gallon = $3.47.
Therefore, the cost of the gas used for Ryosuke to drive his friend back home from work is approximately $3.47, rounded to the nearest cent.
To learn more about subtract click here:
brainly.com/question/13619104
#SPJ11
PLEASE HELP AND PLEASEEEE SOLVE WITH EXPLANATION PLEASE OR I WILL REPORT LIKE FOR THE 18TH TIME PLEASE

Answers
Answer:
The surface area of the given cylinder is 803.8 in² to the nearest tenth.
Step-by-step explanation:
The formula for the surface area of a cylinder is:
\(\boxed{SA = 2\pi r^2 + 2\pi rh}\)
where r is the radius of the circular base, and h is the height of the cylinder.
From inspection of the given diagram:
r = 8 inh = 8 inπ = 3.14Substitute these values into the formula and solve for SA:
\(\begin{aligned}\implies SA&=2\pi r^2 + 2\pi rh\\&=2 \cdot 3.14 \cdot 8^2+2 \cdot 3.14 \cdot 8 \cdot 8\\&=2 \cdot 3.14 \cdot 64+2 \cdot 3.14 \cdot 8 \cdot 8\\&=401.92+401.92\\&=803.84\\&=803.8\; \sf in^2\;\;(nearest \; tenth)\end{aligned}\)
Therefore, the surface area of the given cylinder is 803.8 in² to the nearest tenth.
Question :-
What is the surface area of the cylinder that has a radius of 8 in and a height of 8 in?Answer :-
The surface area of the cylinder is 803.8 in². Thus, the 3rd option makes it the correct answer.\( \rule{180pt}{3pt}\)
Diagram :-
\(\setlength{\unitlength}{1mm}\begin{picture}(5,5)\thicklines\multiput(-0.5,-1)(26,0){2}{\line(0,1){40}}\multiput(12.5,-1)(0,3.2){13}{\line(0,1){1.6}}\multiput(12.5,-1)(0,40){2}{\multiput(0,0)(2,0){7}{\line(1,0){1}}}\multiput(0,0)(0,40){2}{\qbezier(1,0)(12,3)(24,0)\qbezier(1,0)(-2,-1)(1,-2)\qbezier(24,0)(27,-1)(24,-2)\qbezier(1,-2)(12,-5)(24,-2)}\multiput(18,2)(0,32){2}{\sf{8 \: in}}\put(9,17.5){\sf{8 \: in}}\end{picture}\)
Solution :-
As per the provided information in the given question, we have been given that the radius of the cylinder is 8 in. The height of the cylinder is 8 in. We have been asked to find or calculate the surface area of the cylinder.
To calculate the surface area of the cylinder, we will use the formula below :-
\(\bigstar \:\:\:\boxed{\sf{\:\:Surface \: Area_{(Cylinder)} = 2\pi r^2 + 2\pi rh \:\:}}\)
Substitute the given values into the above formula and solve for surface area:
\(\sf:\implies Surface \: Area_{(Cylinder)} = 2\pi r^2 + 2\pi rh\)
\(\sf:\implies Surface \: Area_{(Cylinder)} = (2)(3.14)(8 \: in)^2 + (2)(3.14)(8\:in)(8\:in) \)
\(\sf:\implies Surface \: Area_{(Cylinder)} = (2)(3.14)(64 \: in^2) + (2)(3.14)(64\:in^2) \)
\(\sf:\implies Surface \: Area_{(Cylinder)} = (2)(200.96 \: in^2) + (2)(200.96 \: in^2) \)
\(\sf:\implies Surface \: Area_{(Cylinder)} = 401.92 \: in^2 + 401.92 \: in^2 \)
\(\sf:\implies \bold{Surface \: Area_{(Cylinder)} = 803.84 \: in^2}\)
Therefore :-
The surface area of the cylinder is 803.8 in². Thus, the 3rd option makes it the correct answer.\(\\\)
Learn more about the surface area of the sphere at https://brainly.com/question/28988747
Have a great day! <33
One effect of glasnost was that Responses A. governments in Eastern Europe introduced reforms. B. people in Western Europe protested against their governments. C. factories in the Soviet Union became more efficient. D. governments in Eastern Europe remained communist.
Answers
One effect of glasnost was that A) governments in Eastern Europe introduced reforms.
The correct response is A) governments in Eastern Europe introduced reforms.
Glasnost, meaning "openness" in Russian, was a policy introduced in the Soviet Union by Soviet leader Mikhail Gorbachev in the 1980s. It aimed to promote transparency, political openness, and freedom of expression. While Glasnost primarily affected the Soviet Union, its impact also extended to Eastern European countries under Soviet influence.
As a result of Glasnost, governments in Eastern Europe began introducing reforms. The policy led to a loosening of restrictions on freedom of speech, press, and political dissent. It created an atmosphere of increased openness and public discussion, which facilitated demands for political and social change.
In countries such as Poland, Hungary, Czechoslovakia, and East Germany, the push for reform gained momentum. Popular movements and protests emerged, advocating for greater political rights, democracy, and economic reforms. This eventually led to significant political transformations, including the fall of communist governments in some Eastern European countries.
Therefore, the effect of Glasnost was that governments in Eastern Europe introduced reforms, marking a shift away from the rigid communist system and towards more democratic and open societies.
To learn more about Eastern Europe here:
https://brainly.com/question/31732912
#SPJ4
3) (2 Marks) Find the range and codomain of the matrix transformation T A
, where A= \( {\left[\begin{array}{cc}1 & 2 \\ 1 & -2 \\ 0 & 1\end{array}\right] \). Is the result true if the functions are not linear? Justify your \( } \) answer.
Answers
T A can be seen as a linear transformation from R^2 to R^3.
To find the range and codomain of the matrix transformation T A, we need to first determine the matrix T A . The matrix T A is obtained by multiplying the input vector x by A:
T A (x) = A x
Therefore, T A can be seen as a linear transformation from R^2 to R^3.
To determine the range of T A , we need to find all possible outputs of T A (x) for all possible inputs x. Since T A is a linear transformation, its range is simply the span of the columns of A. Therefore, we can find the range by computing the reduced row echelon form of A and finding the pivot columns:
A = (\left[\begin{array}{cc}1 & 2 \ 1 & -2 \ 0 & 1\end{array}\right]) ~ (\left[\begin{array}{cc}1 & 0 \ 0 & 1 \ 0 & 0\end{array}\right])
The pivot columns are the first two columns of the identity matrix, so the range of T A is spanned by the first two columns of A. Therefore, the range of T A is the plane in R^3 spanned by the vectors [1, 1, 0] and [2, -2, 1].
To find the codomain of T A , we need to determine the dimension of the space that T A maps to. Since T A is a linear transformation from R^2 to R^3, its codomain is R^3.
If the functions were not linear, it would not make sense to talk about their range or codomain in this way. The concepts of range and codomain are meaningful only for linear transformations.
Learn more about linear from
https://brainly.com/question/2030026
#SPJ11
Please help me. I have so much late work I need this asap;

Answers
Answer: 7, 6 ,7
Step-by-step explanation:
School fees for a popular high school have been increasing by 9.5% per year. When Antoinette started the school, the annual fees were $6230. By the time Antoinette leaves the school 8 years later, how much have her parents paid in school fees in total? Give your answer to the nearest $100.
Answers
Answer:
Antoinette's parents paid $ 70000 by the time she left the school.
Step-by-step explanation:
Antoinette's parents paid at the beginning (\(t = 0\)) $ 6230, and each year paid annual fees including increases seven times. (\(0 <t \leq 7\)) We find that annual fee paid at a given year is represented by the following formula:
\(C(t) = C_{o}\cdot \left(1+\frac{r}{100} \right)^{t}\)
Where:
\(C_{o}\) - Initial annual fees, measured in US dollars.
\(C(t)\) - Current annual fees, measured in US dollars.
\(r\) - Yearly increase rate, dimensionless.
If we know that \(C_{o} = \$\,6230\) and \(r =9.5\), first 8 annual fees paid by Antoinette's parents are:
\(C(0) = \$\,6230\)
\(C(1) =\$\,6821.85\)
\(C(2) = \$\,7469.93\)
\(C(3) = \$\,8179.57\)
\(C(4) = \$\,8956.63\)
\(C(5) = \$\,9807.51\)
\(C(6) = \$\,10739.22\)
\(C(7) = \$\,11759.45\)
Now, we sum each yearly fees to determine the total paid by Antoinette's parents when she leaves the school at the end of the 8th year.
\(C_{T} = C(0) +C(1)+C(2) + C(3)+C(4)+C(5)+C(6)+C(7)\)
\(C_{T} = \$\,6230+\$\,6821.85+\$\,7469.93+\$\,8179.57+\$\,8956.63+\$\,9807.51+\$\,10739.22+\$\,11759.45\)
\(C_{T} = \$\,69964.16\)
Antoinette's parents paid $ 70000 by the time she left the school.
is 1/5-x equivalent to x-1/5
Answers
some children were asked to name their favourite flavour of ice cream the pie chart and table show some information about their answers

Answers
Answer:
mint ----> 6
strawberry ----> 105
chocolate -----> 16
Step-by-step explanation:
90° ------> 12
so , 15° -----> 2
mint ---> 45° --> 15°× 3 ---> 2×3 --> 6
strawberry ---> 14 ---> 2×7 ---> 15° × 7 -->105°
chocolate ---> 120° ---> 8×15° --> 8×2 ---> 16
Yes, the pie chart and table show some information about the children's favorite ice cream flavors.
The pie chart shows that the most popular flavor is chocolate, with 30% of the children choosing it. Vanilla is the second most popular flavor, with 25% of the children choosing it. Strawberry is the third most popular flavor, with 20% of the children choosing it. The other flavors are less popular, with each receiving less than 10% of the votes.
The table shows the number of children who chose each flavor. There were 15 children who chose chocolate, 12 children who chose vanilla, 10 children who chose strawberry, 4 children who chose mint, 3 children who chose cookies and cream, and 2 children who chose coffee.
The pie chart and table together provide a good overview of the children's favorite ice cream flavors. Chocolate is the clear favorite, followed by vanilla and strawberry. The other flavors are less popular, but they still have some fans.
Here is a table that summarizes the information from the pie chart and table:
Flavor Number of Children Percentage
Chocolate 15 30%
Vanilla 12 25%
Strawberry 10 20%
Mint 4 10%
Cookies and cream 3 7.5%
Coffee 2 5%
To learn more about pie chart here:
https://brainly.com/question/29148468
#SPJ2
Is 3 times the same as 300%?
Answers
Answer: no
Step-by-step explanation: 3 is the same as 0.03% and 300% is the same as 3%.
PLEASE HELP
Lateena solved the equation below. Is her solution correct? Explain why or why not.
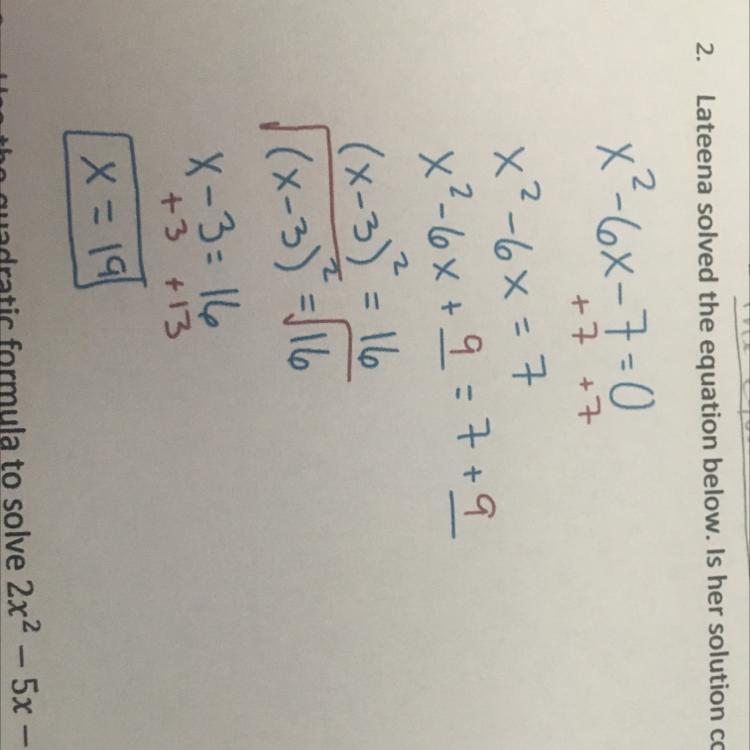
Answers
Answer:
it isn't correct
\(x {}^{2} - 6x - 7 = 0 \\ d = 36 + 28 = 64 \\ x1 = \frac{6 - 8}{2} = - 1 \\ x2 = \frac{6 + 8}{2} = 7\)
Answer:
her solution isn't correct .
because she had done a slight mistake in her calculation.
i.e.
\(\sqrt{16}=4 \:\:not \:\:16\)
Step-by-step explanation:
solution given:
x²-6x-7=0
making it a perfect square
we must make it on the form of (a+b)²or(a-b)²
so
x²-2*3*x+3²-3²-7=0
(x-3)²-9-7=0
(x-3)²-16=0
adding 16 on both aide
(x-3)²=16
doing square root on both side
\(\sqrt{(x-3)²}=\sqrt{16}\)
x-3=±4
taking positive
x-3=4
adding 3 on both side
x=7
and.
taking negative
x-3=-4
adding 3 on both side
x=-4+3
x=-1
x=-1 or 7
Now, let us convert a machine code to a MIPS instruction. Locate address 0x00400010 from the Text
Segment window.
a. What is the machine code at this address in hex? Convert this code into binary.
b. From the binary version of this machine code. What is the instruction type? How can you tell? How
many fields are there in this instruction type? What are the names of these fields?
c. According to the binary machine code, what is the value of each field in hex?
d. Refer to the MIPS sheet, what operation is this instruction? How can you tell? What is the mapping
of the registers being used in this instruction?
e. What is the final MIPS instruction? Is it the same as the Source Column in the Text Segment
window?
Answers
The final MIPS instruction is lw $0, 0($4). This is the same as the Source Column in the Text Segment window. To answer this question, we should first locate the address 0x00400010 in the Text Segment window, which will show you the machine code at this address in hexadecimal format.
a. Next, convert this hexadecimal code to binary.
b. After obtaining the binary version of the machine code, you need to determine the instruction type by examining the opcode (the first 6 bits of the binary code). Based on the opcode, you can identify whether it is an R-type, I-type, or J-type instruction. The number of fields and their names differ for each instruction type:
- R-type: 6 fields (opcode, rs, rt, rd, shamt, funct)
- I-type: 4 fields (opcode, rs, rt, immediate)
- J-type: 2 fields (opcode, address)
c. To find the value of each field in hexadecimal, first identify the binary bits corresponding to each field based on the instruction type determined in step b. Then, convert each field from binary to hexadecimal.
d. To identify the operation and mapping of the registers, refer to the MIPS reference sheet. Match the opcode and (if applicable) the funct code to the corresponding operation. For R-type instructions, also identify the source registers (rs, rt) and the destination register (rd). For I-type instructions, identify the source register (rs), the target register (rt), and the immediate value. For J-type instructions, there is no register mapping.
e. The final MIPS instruction can be determined by combining the operation and register mappings obtained in step d. Compare this instruction to the one in the Source Column of the Text Segment window to verify if they are the same.
a. The machine code at address 0x00400010 in hex is 0x8fa40000. Converting this to binary gives us 10001111101001000000000000000000.
b. From the binary version of the machine code, we can see that this is an I-type instruction. We can tell because the first six digits (100011) correspond to the opcode for an I-type instruction. There are three fields in this instruction type: opcode, rs, and immediate.
c. The value of each field in hex is opcode (0x8), rs (0x14), and immediate (0x0).
d. According to the MIPS sheet, this instruction is an lw (load word) operation. We can tell because the opcode (0x8) corresponds to lw on the sheet. The mapping of registers being used in this instruction is: $4 (rs) and $0 (rt) are being used, and the immediate value (0x0) is being added to the value in $4 to get the memory address to load from.
e. The final MIPS instruction is lw $0, 0($4). This is the same as the Source Column in the Text Segment window.
Learn more about hexadecimal here: brainly.com/question/28875438
#SPJ11
The Nearly Normal condition is met in one of either of two ways: the sample size is large or...
a.the population (and sample) distribution are already normal distribtuions.
b.we know the standard deviation of the population.
c.if the units we are measuring can only be positive (e.g. weights of chickens).
d.the two samples are independent.
Answers
The correct answer is b. we know the standard deviation of the population.
The Nearly Normal condition, also known as the Central Limit Theorem, states that the sampling distribution of the sample mean tends to be approximately normal, even if the population distribution is not normal, under certain conditions. One way to meet the Nearly Normal condition is by knowing the standard deviation of the population.
When the standard deviation of the population is known, the sample size does not have to be large for the sampling distribution of the sample mean to be approximately normal. This is because the standard deviation provides information about the variability of the population, allowing for a more accurate estimation of the sample mean distribution.
While the other options (a, c, and d) may be relevant in specific scenarios, they are not directly related to meeting the Nearly Normal condition as defined by the Central Limit Theorem.
To learn more about deviation click here:brainly.com/question/31835352
#SPJ11
A baseball card that was valued at $200 in 1980 has increased in value by 7% each year. Write a function to model this situation, then find the value of the card in 2016
Answers
Answer:
$2284.6
Step-by-step explanation:
Given data
Principal= $200
Rate= 7%
Time= 1980-2016= 36 years
The expression for the exponential model is given as
A= P(b)^t
b=1+r-----------because will are dealing with increase
A= P(1+r)^t
A=200(1+0.07)^36
A= 200(1.07)^36
A= 200*11.423
A=$2284.6
The value of the card is $2284.6
The area of a square is 81 cm 2 . Find the perimeter of the square.
PLEASE ANSWER!!!
Answers
Answer:
36
Step-by-step explanation:
9 times 4 buddy
area = 81 so side length ^2 = 81
square root each side
side length = 9
perimeter of square = 4 x side length
= 4 x 9 = 36cm
La suma de dos números es 15 y la suma de sus cuadrados es 113. ¿Cuáles son los números?
Answers
La suma de dos números es 15 y la suma de sus cuadrados es 113. Por lo tanto, los dos números son 7 y 8.
Para resolver este problema, podemos utilizar el método de sustitución. Si llamamos a los dos números "x" e "y", podemos plantear dos ecuaciones con la información que nos dan:
x + y = 15 (ecuación 1)
x² + y² = 113 (ecuación 2)
De la primera ecuación, podemos despejar a "y" para obtener:
y = 15 - x
Ahora, podemos sustituir este valor de "y" en la segunda ecuación:
x² + (15 - x)² = 113
Expandiendo y simplificando:
x² + 225 - 30x + x² = 113
2x^2 - 30x + 112 = 0
Esta es una ecuación cuadrática que podemos resolver utilizando la fórmula general:
x = (-b ± sqrt(b² - 4ac)) / 2a
Donde:
a = 2
b = -30
c = 112
Sustituyendo:
x = (-(-30) ± sqrt((-30)² - 4(2)(112))) / 2(2)
x = (30 ± sqrt(900 - 896)) / 4
x = (30 ± 2) / 4
Esto nos da dos posibles valores para "x":
x₁ = 8
x₂ = 7
Para encontrar los valores correspondientes de "y", podemos utilizar la ecuación que obtuvimos antes:
y = 15 - x
Así que:
y₁ = 15 - 8 = 7
y₂ = 15 - 7 = 8
Por lo tanto, los dos números son 7 y 8.
To learn more about cuadrática refer here:
https://brainly.com/question/24999712
#SPJ11
you need to add lines, segments, and angles to create your ultimate circle. you need to incorporate specific theorems. Each problem must ask for a missing measure(an arc measure, segment length or angle measure. Provide information that someone would need to solve at the top of the puzzle could include angle measures, arc measures, tangent lines, parallel ect. You must list which problem number is used for each listed theorem show all work.

Answers
Some information that someone might use to solve problems related to a circle design is the Tangent Arc theorem.
What is the tangent arc theorem?The tangent arc theorem states that if an angle is formed by two secants, one secant, one tangent, or two tangents, and also intersects in a space outside of the circle, then the value obtained will be equal to the difference of the values of the intercepted arcs divided by one and a half.
Also, note that angles outside a circle are those whose vertex or arc is pointed outwards and their sides are either secants or tangents. With this information, it will be possible to solve problems related to tangent lines and arc measures.
Learn more about the tangent arc theorem here:
https://brainly.com/question/29239907
#SPJ1
As it is used in line 19, the phrase paid out most nearly
means:
F. dispensed.
G. ascertained.
H. suggested.
J. compensated.
Answers
Answer:
Dispensed
Step-by-step explanation:
Determine whether the planes are parallel, perpendicular or neither. 2x â 4y + 3z = 5, x + 8y + 10z = 3
Answers
The given two planes 2x + 4y + 3z = 5 and x + 8y + 10z = 3 are perpendicular to each other.
According to the given question.
We have two planes
2x - 4y + 3z = 5
and,
x + 8y + 10z = 3
Since, two planes are perpenicular if
\(a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0\)
Where \(a_{1}\), \(b_{1}\) and \(c_{1}\) and \(a_{2}\), \(b_{2}\) and \(c_{2}\) are the direction ratios of planes.
And the two planes are parallel to each other if
\(\frac{a_{1} }{a_{2} } =\frac{b_{1} }{b_{2} } = \frac{c_{1} }{c_{2} }\)
Here, the direction ratios of plane 2x + 4y + 3z = 5 are 2, -4, and 3 and the direction ratios of plane x + 8y + 10z = 3 are 1, 8, and 10
Now,
2(1) + (-4)(8) + 3(10)
= 2 - 32 + 30
= 0
Since, the sum of the product of the direction ratios of the two palnes is 0. Therefore, the given two planes 2x + 4y + 3z = 5 and x + 8y + 10z = 3 are perpendicular to each other.
Find out more information about perpendicular and parallel planes here:
https://brainly.com/question/19580509
#SPJ4
Sally is planning the school picnic and needs to decide what food vendor to use. She asks 800 students whether they would rather have a taco truck or a fruit smoothie cart. The results of the survey are shown in the table.What is the relative frequency of eighth graders who want fruit smoothies?A. 0.15B. 0.30C. 0.44D. 0.19

Answers
number of eighth-graders who want fruit smoothies: 150
total number of students: 800
relative frequency: 150/800 = 3/16 ≈ 0.19
33, 25, 42, 25, 31, 37, 46, 29, 38 what is the interquartile range of the data?
Answers
The interquartile range of the data will be 13
When arranged from lowest to highest, the IQR reflects the median 50% of values. To calculate the interquartile range (IQR), firstly compute the median (middle value) of the data's lower and upper halves. All those are quartile 1 (Q1) and quartile 3 (Q3) values (Q3). The interquartile range is the difference between quarters three and then one.
first, let us sort the data from lowest to highest
25,25,29,31,33,37,38,42,46
Q1- median of the lower half of the data=(29+25)/2=27
Q3-median of the upper half of the data=(38+42)/2=40
the interquartile range of the data will be Q3-Q1
40-27= 13
Learn more about interquartile range here:https://brainly.com/question/17083142
#SPJ4
PLEASE HELP FAST!!! Find the surface area of the composite figure. Round your answer to the nearest tenth if necessary.

Answers
The surface area of the composite figure is 524 square meters
Surface area of a figureThe given composite figure is made up of a triangular prism and a rectangular prism. The surface area of the figure is given as:
Surface area = 2(16*5+5*4+16*4) + (16*6) + 2(50)
Take the sum
Surface area = 2(80+20+64) + 96 + 100
Surface area = 2(164) +196
Surface area = 328 + 196
Surface area = 524 square meters
Hence the surface area of the composite figure is 524 square meters
Learn more on surface area here: https://brainly.com/question/1297098
#SPJ1
If a fair die is rolled 7 times, what is the probability, rounded to the nearest thousandth, of getting at most 2 twos?
Answers
Answer:
0.904
Step-by-step explanation:
Using the binomial distribution, it is found that there is a 0.905 = 90.5% probability of getting at most 2 twos.
For each time the die is rolled, there are only two possible outcomes, either the result is a 2, or it is not. The result on a roll is independent of any other roll, which means that the binomial distribution is used to solve this question.
Binomial probability distribution
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes. n is the number of trials. p is the probability of a success on a single trial.In this problem:
The die is rolled 7 times, hence \(n = 7\).One out of the 6 sides is a 2, hence \(p = \frac{1}{6} = 0.1667\)The probability is:
\(P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)\)
Hence:
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{7,0}.(0.1667)^{0}.(0.8333)^{7} = 0.279\)
\(P(X = 1) = C_{7,1}.(0.1667)^{1}.(0.8333)^{6} = 0.391\)
\(P(X = 2) = C_{7,2}.(0.1667)^{2}.(0.8333)^{5} = 0.235\)
Then:
\(P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.279 + 0.391 + 0.235 = 0.905\)
0.905 = 90.5% probability of getting at most 2 twos.
A similar problem is given at https://brainly.com/question/24863377
What is 4.5pi minus pi/0.5?
Answers
Answer:
≈ 7.8598
Step-by-step explanation:
Let's round pi to 3.14159. First, we multiply 3.14159 by 4.5, which is around 14.13716. Then, we divide 3.14159 by 0.5, which is around 6.28318. So, 14.13716 - 6.28318 = 7.8598
What is remainder when x3 2x² X 1 is divided by x 1?
Answers
When x^3+2x^2+x+1 is divided by (x+1) then remainder is 1.
In the given question, we have to find what is remainder when x^3+2x^2+x+1 is divided by (x+1).
To find the remainder there are two ways. First we divide the x^3+2x^2+x+1 by (x+1). Second we find the value of from (x+1) by equating (x+1) equal to zero. The put the value of x in the expression x^3+2x^2+x+1.
In this we ca easily find the remainder.
Now we firstly find the value of x;
(x+1) = 0
Subtract 1 on both side we get;
x= −1
Now put x= -1 in the expression x^3+2x^2+x+1.
x^3+2x^2+x+1 = (−1)^3+2(−1)^2+(−1)+1
x^3+2x^2+x+1 = −1+2−1+1
x^3+2x^2+x+1 = 1
Hence, when x^3+2x^2+x+1 is divided by (x+1) then remainder is 1.
To learn more about division of polynomial link is here
brainly.com/question/29718477
#SPJ4
The right question is:
What is remainder when x^3+2x^2+x+1 is divided by (x+1)?
You have 2 positive numbers. One number is one-fifth of the other number. The difference between the two numbers is 228, find the numbers.
Answers
Hey there! I'm happy to help!
Let's call these numbers x and y and model the information we have.
x=1/5y
y-x=228 (we see that x is smaller than y in the first equation, so we put it second )
We see that x is equal to 1/5y. We can switch the x in the second equation with 1/5y and solve for y.
y-1/5y=228
4/5y=228
We divide both sides by 4/5.
y=285
We know that x is 1/5 of y, so we divide by 5.
285/5=57
x=57
So, our numbers are 57 and 285.
Have a wonderful day! :D
The 2 positive numbers are 285 and 57 and they have a difference of 228.
EquationAn equation is an expression used to show the relationship between two or more numbers and variables.
Let x represent the bigger positive number and y the smaller number. Hence:
y = (1/5)x y - (1/5)x = 0 (1)Also:
x - y = 228 (2)Solving equation 1 and 2 simultaneously gives:
x = 285, y = 57
The 2 positive numbers are 285 and 57 and they have a difference of 228.
Find out more on equation at: https://brainly.com/question/13763238
the qualified applicant pool for four management trainee positions consists of nine women and seven men. (a) how many different groups of applicants can be selected for the positions? (b) how many different groups of trainees would consist entirely of women? (c) probability extension: if the applicants are equally qualified and the trainee positions are selected by drawing the names at random so that all groups of four are equally likely, what is the probability that the trainee class will consist entirely of women? (round your answer to four decimal places.)
Answers
There are 1820 different groups of applicants for 4 management trainee positions, 126 different groups of trainees consisting entirely of women, and a 0.0692 probability that the trainee class will consist entirely of women.
The number of different groups of applicants that can be selected for the four management trainee positions can be calculated using the combination formula:
nCr = n! / (r! * (n-r)!)
where n is the total number of applicants (16 in this case) and r is the number of positions to be filled (4 in this case).
So the number of different groups of applicants that can be selected is:
16C4 = 1820
Therefore, there are 1820 different groups of applicants that can be selected for the four management trainee positions.
The number of different groups of trainees that would consist entirely of women can be calculated using the combination formula again, but this time we are selecting all 4 positions from the 9 female applicants:
9C4 = 126
Therefore, there are 126 different groups of trainees that would consist entirely of women.
Assuming that all groups of four are equally likely to be selected, the probability that the trainee class will consist entirely of women can be calculated by dividing the number of different groups of trainees that consist entirely of women (126) by the total number of different groups of applicants (1820):
Probability = 126 / 1820 = 0.0692
So the probability that the trainee class will consist entirely of women is 0.0692 (rounded to four decimal places).
To know more about Probability:
https://brainly.com/question/11234923
#SPJ4
Find the measure of the are or angle indicated. Assume that lines which appear tanget are tangents
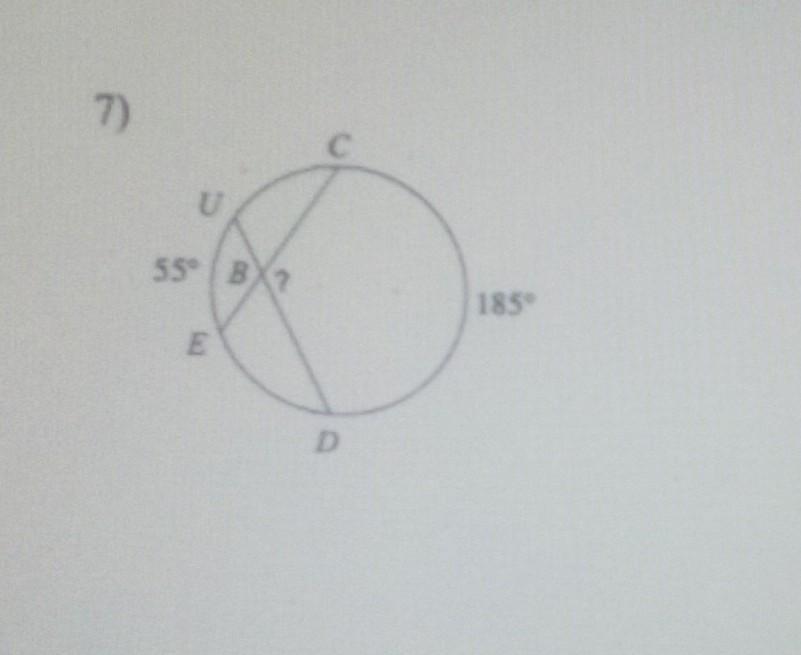
Answers
Given:
In a circle, two chords CE and DU intersect each other inside the circle at B.
Measure of arc CD = 185 degrees.
Measure of arc EU = 55 degrees.
To find:
The measure of angle CBD.
Solution:
Intersecting chords theorem: According to this theorem, if two chords intersect each other inside the circle then the measure of angle on the intersection is half of the sum of intercepted arcs.
Using Intersecting chords theorem, we get
\(m\angle CBD =\dfrac{1}{2}(arcCD+arcEU)\)
\(m\angle CBD =\dfrac{1}{2}(185^\circ +55^\circ )\)
\(m\angle CBD =\dfrac{1}{2}(240^\circ )\)
\(m\angle CBD =120^\circ\)
Therefore, the measure of angle CBD is 120 degrees.
Compare 0.79 and 0.789.
Answers
Answer:
0.79 greater than 0.789 by 0.001
Step-by-step explanation:
\({ \tt{ \delta x + 0.79 = 0.789}} \\ { \tt{ \delta x = 0.001}}\)
Find the pattern rule for 3, 3, 2, 1
Answers
Answer:
add 0, subtract 1, subtract 1
then the pattern restarts
Step-by-step explanation:
Hope this helps