Answers
Answer: the slope is 2
Step-by-step explanation:
It goes up 2 and over 1
y/x
rise over run= rise/run
Related Questions
Question 11 of 25
Company A charges a $120 annual fee plus $7 per hour car share fee.
Company B charges $100 plus $9 per hour. What is the minimum number of
hours that a car share needs to be used per year to make company A a better
deal?
A. 12
B. 11
O C. 10
D. 9
Answers
Answer: is A
Step-by-step explanation:
Divide round your answer to the nearest hundredth 5608.67÷7
Answers
Answer:
5608.67 ÷ 7 = 801.24
3. A car is traveling at a speed of 60 miles per hour. What's the dependent variable in this situation?
A. The speed at which the car travels
B. The age of the car
C. The number of hours the car has traveled
D. The distance the car has traveled
Answers
Answer:
The answer is A) the speed at which the car has traveled
Step-by-step explanation:
Determine what type of quadrilateral ABCD is, given the points. A(2,0) B(3,5) C(5,0) D(6,5) Rhombus Parallelogram Rectangle I know you find the distance formula, but I’m actually confuse in how to KNOW which quadrilateral it is.
Answers
Answer:
Brainliest!!!
Step-by-step explanation:
quadrilateral
is
DescriptionIn Euclidean plane geometry, a quadrilateral is a polygon with four edges and four vertices or corners.
In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length.
In Euclidean geometry, a parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure.
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal. It can also be defined as a parallelogram containing a right angle
Answer:
Parallelogram
Step-by-step explanation:
A quadrilateral is a shape with only 4 lines.
Such as: Square, Kite, Rhombus etc

A square has an area of 4 ft?. What is the length of each side?
Answers
Answer:
2
Step-by-step explanation:

A square has an area of 4 square feet. Then the side length of the square will be 2 feet.
What is the area of the square?Let a be the side length of the square.
Then the area of the square will be
Area of the square = a² square units
A square has an area of 4 square feet.
Then the side length of the square will be
A = a²
4 = a²
a = √4
a = 2 feet
More about the area of the square link is given below.
https://brainly.com/question/1658516
#SPJ2
Evaluate the following functions.
Help

Answers
And you do the same thing for the second equation except this has -1 for x so you get 2(-1)^2+4(-1)+9 which equals 2-4+9=7. Make sense? Hope this helps
8 ft
10 ft
Find the perimeter of this figure to
the nearest hundredth.
Use 3.14 to approximate .
P = [?] ft
Notice that only half of the circle is included in the figure!
Answers
The perimeter of the figure is 4(π + 9)ft.
What is perimeter?A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length.
Given is a 2 - D figure as shown in the figure attached.
We can write the perimeter as -
P = P{rectangle} + P{semicircle}
P = 2(10 + 8) + (4π)
P = (4π) + (36)
P = 4(π + 9)
Therefore, the perimeter of the figure is 4(π + 9)ft.
To solve more questions on Perimeter, visit the link below -
https://brainly.com/question/14996609
#SPJ1
![8 ft10 ftFind the perimeter of this figure tothe nearest hundredth.Use 3.14 to approximate .P = [?] ftNotice](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/dFiczUV1VJQw8I5GGyu3EvpqmHvY45W3.png)
4x + 3c = -2 ... solve for X
Answers
Answer:
Step-by-step explanation:
4x + 3c = -2
4x = -2 - 3c
x = (-2 - 3c)/4
Missing numbers
, 9.8 , 9.1
Answers
Answer:
10.5
Step-by-step explanation:
Missing number, 9.8, 9.1
We see that each time it subtracts 0.7
We take
9.8 + 0.7 = 10.5
So, the missing number is 10.5
Fran is training for her first marathon, and she wants to know if there is a significant difference between the mean number of miles run each week by group runners and individual runners who are training for marathons. She interviews 38 randomly selected people who train in groups, and finds that they run a mean of 49.5 miles per week. Assume that the population standard deviation for group runners is known to be 1.1 miles per week. She also interviews a random sample of 33 people who train on their own and finds that they run a mean of 48.5 miles per week. Assume that the population standard deviation for people who run by themselves is 2.6 miles per week. Test the claim at the 0.01 level of significance. Let group runners training for marathons be Population 1 and let individual runners training for marathons be Population 2.
Required:
Draw a conclusion and interpret the decision.
Answers
Answer:
conclude that there is no significant evidence to support the claim that difference exists between the mean number of miles run by the two groups.
Step-by-step explanation:
H0 : μ1 = μ2
H0 : μ1 ≠ μ2
The test statistic :
(x1 - x2) / √(s1²/n1) + (s2²/n2)
(49.5 - 48.5) / √(1.1²/38) + (2.6²/33)
1 / √0.2366905
Test statistic = 2.055
Using the Pvalue from Tstatistic calculator :
df = (smaller sample - 1) = 33 - 1 = 32
Pvalue from Test score calculator = 0.048
Pvalue > α ; Fail to reject the null ;
Hence, conclude that there is no significant evidence to support the claim that difference exists between the mean number of miles run by the two groups.
I need help so bad somebody please help me with math ;-;:
what is the answer?
X 2 4 8 10 16
Y 1 2 4 5 8
1.y = 2 x
2.y = 1 x
3.y = x - 1
4.y = x ÷ 2
Answers
Answer:
y=x/2 (x divided by 2)
Step-by-step explanation:
2/1=1,4/2=2,8/2=4,10/2=5,16/2=8
What is the cost of 6 pencils at 60 cents a dozen
Answers
To determine the cost of 6 pencils at 60 cents a dozen, we need to convert the price per dozen to the price per pencil. We know that a dozen is equal to 12, so we can use the following formula:
Price per pencil = (Price per dozen) / (Number of items per dozen)
So, in this case:
Price per pencil = (60 cents) / (12 pencils)
To convert cents to dollars, we divide by 100.
Price per pencil = (60/100) $ = 0.6 $
To find the total cost for 6 pencils we multiply the price per pencil by the number of pencils
Cost of 6 pencils = 6 * 0.6 = 3.6 $
So the cost of 6 pencils at 60 cents a dozen is 3.6 $.
can u help me I really need the help so please help me
Answers
Answer:
what's the question?
A summary of the two stocks is shown.
Name of Stock Symbol Closing Price Day 1 Closing Price Day 2 Closing Price Day 3
Metropolis, Ltd MTP 17.95 18.25 18.28
Suburbia, Inc SBR 5.63 4.98 5.25
Suppose you purchase 65 shares of Metropolis stock and 50 shares of Suburbia stock on Day 1 at the closing price. Which day, during the following two days, would be the best to sell both stocks and by how much?
Day 2 is the best by $13.00.
Day 3 is the best by $13.00.
Day 2 is the best by $2.45.
Day 3 is the best by $2.45.
Answers
The day, from the following two days, which would be the best to sell both stocks with the closing price is day 3 by an amount of $2.45.
Given are the closing prices of two stocks in three days.
If you purchase 65 shares of Metropolis stock and 50 shares of Suburbia stock on Day 1 at the closing price,
Amount invested = (65 × 17.95) + (50 × 5.63) = $1448.25
If the stock is sold in day 2,
Amount received = (65 × 18.25) + (50 × 4.98) = $1435.25
Profit = $1435.25 - $1448.25 = -$13
If the stock is sold in day 3,
Amount received = (65 × 18.28) + (50 × 5.25) = $1450.7
Profit = $1450.7 - $1448.25 = $2.45
The profit is more for day 3 than day 2.
Hence it is best to sell on day 3 by $2.45.
Learn more about Stocks here :
https://brainly.com/question/14270259
#SPJ1
. Why is the following arrangment of squares not an array?
Answers
When it comes to arrays in mathematics, it usually involves objects or numbers that are arranged in rows and columns.In order for a set of squares to be considered an array, it must meet certain requirements. These requirements are:All rows must have the same number of squares. All columns must have the same number of squares. Squares must be organized in an orderly manner. A set of squares that does not meet these requirements is not an array.
An array is a set of objects or values that are organized in a specific order. It is used in programming, mathematics, and other fields to make data manipulation and analysis easier.
When it comes to arrays in mathematics, it usually involves objects or numbers that are arranged in rows and columns.In order for a set of squares to be considered an array, it must meet certain requirements. These requirements are:All rows must have the same number of squares. All columns must have the same number of squares. Squares must be organized in an orderly manner. A set of squares that does not meet these requirements is not an array.
For example, if a set of squares is arranged in a random or disorganized manner, it cannot be considered an array because it does not meet the orderly requirement. Additionally, if the number of squares in each row or column is different, it cannot be considered an array because it does not meet the uniformity requirement.
Overall, it is important to remember that an array is a specific type of organization and cannot be applied to any random set of objects or values.
For more such questions on arrays, click on:
https://brainly.com/question/28061186
#SPJ8
A recent study reported that 73% of Americans could only converse in one language. A random sample of 130 Americans was randomly selected. What is the probability that 100 or fewer of these Americans could only converse in one language?
Answers
Answer:
Probability that 100 or fewer of these Americans could only converse in one language is 0.8599.
Step-by-step explanation:
We are given that a recent study reported that 73% of Americans could only converse in one language.
A random sample of 130 Americans was randomly selected.
Let \(\hat p\) = sample proportion of Americans who could only converse in one language.
The z score probability distribution for sample proportion is given by;
Z = \(\frac{\hat p-p}{\sqrt{\frac{\hat p(1-\hat p)}{n} } }\) ~ N(0,1)
where, p = population proportion of Americans who could only converse in one language = 73%
\(\hat p\) = sample proportion = \(\frac{100}{130}\) = 0.77
n = sample of Americans = 130
Now, probability that 100 or fewer of these Americans could only converse in one language is given by = P( \(\hat p\) \(\leq\) 0.77)
P( \(\hat p\) \(\leq\) 0.77) = P( \(\frac{\hat p-p}{\sqrt{\frac{\hat p(1-\hat p)}{n} } }\) \(\leq\) \(\frac{0.77-0.73}{\sqrt{\frac{0.77(1-0.77)}{130} } }\) ) = P(Z \(\leq\) 1.08) = 0.8599
The above probability is calculated by looking at the value of x = 1.08 in the z table which has an area of 0.8599.
if Penelope's car has an average fuel consumption of 3 miles per gallon and she uses 9.5 gallons how far did she drive
Answers
Answer:
approximately 3.16 repeated
Step-by-step explanation:
Given parameters:
Average fuel consumption of Penelope's car = 3miles per gallon
Amount of fuel used = 9.5 gallons
Unknown:
Distance of her drive = ?
Solution:
Since her rate of fuel consumption per miles is known, we can simply solve for the distance she covers.
Distance covered = Rate of fuel consumption per miles x amount of fuel used
Distance covered = 3 x 9.5 = 28.5miles
The distance covered by Penelope's car is 28.5miles
PLEASE HELP!!!
Solve this exercise using the fact that the sum of the measures of the three angles of a triangle is 180° In a triangle, the measures of the three angles are x, x + 7, and x - 13. What is the measure of each angle?

Answers
Answer:
The sides are 62, 69, and 49
Step-by-step explanation:
x + (x + 7) + (x - 13) = 180
3x - 6 = 180
3x = 186
x = 62
Side and angle properties of a parallelogram level 2. Find x, y, and z. NO LINKS!!!
Part 2

Answers
Answer:
Solution given:
x=121°[opposite angle of a parallelogram are equal]
<Z=19°
we have
y+z+121°=180°[co interior angle]
y=180-121-19
y=40°
:.x=121°,y=40°& z=19°
Answer:
x=121°y=40°z=19°Step-by-step explanation:
Here the angle A=Angle C
so,
x=121°
z=19°
so,
180=y+z+121180-121=y+1959=y+19y=59-19y=40°dentify on which quadratic function is positive.
Y = 2x^2 - 17x + 30
Identify on which quadratic function is negative.
Y = - x^2 - 6x - 8
A explanation on the answers would be appreciated!
(Lots of points!)
Answers
Step-by-step explanation:
Let us identify which quadratic function is positive. Yeah, let's start.
Y = \({ \red{ \sf{2 {x}^{2} - 17x + 30}}}\)
By using factorisation method,
\({ \red{ \sf{2 {x}^{2} - 12x - 5x + 30}}}\)
Take common factors
\({ \red{ \sf{2x(x - 6) - 5(x - 6)}}}\)
\({ \red{ \sf{(2x - 5)}}} \: \: \: \: \: \: \: || \: \: \: \: \: { \red{ \sf{(x - 6)}}}\)
\({ \red{ \sf{2x - 5 = 0}}} \: \: || \: \: { \red{ \sf{x - 6 = 0}}}\)
\({ \red{ \sf{2x = 5}}} \: \: \: \: \: \: \: \: \: || \: \: \: \: { \red{ \boxed{ \green{ \sf{x = 6}}}}}\)
\({ \red{ \sf{{ \frac{ \cancel2}{ \cancel2}x}}}} = { \red{ \sf{ \frac{5}{2}}}}\)
\({ \red{ \boxed{ \green{ \sf{x = \frac{5}{2}}}}}} \)
____________________________________
Y = \({ \blue{ \sf {{ - x}^{2} - 6x - 8}}}\)
By using factorisation method,
\({ \blue{ \sf{ - {x}^{2} - 2x - 4x - 8}}}\)
Take common factors
\({ \blue{ \sf{ - x(x + 2) - 4(x + 2)}}}\)
\({ \blue{ \sf{( - x - 4)}}} \: \: \: \: \: || \: \: \: \: \: { \blue{ \sf{(x + 2)}}}\)
\({ \blue{ \sf{- x - 4 = 0}}} \: \: \: \: \: || \: \: \: \: \: { \blue{ \sf{x + 2 = 0}}}\)
\({ \blue{ \boxed{ \green{ \sf{x = -4}}}}} \: \: \: \: \: || \: \: \: \: \: { \blue{ \boxed{ \green{ \sf{x = -2}}}}}\)
Hence, the first quadratic function is positive and second quadratic function is negative.
Answer:
\(\textsf{$y = 2x^2 - 17x + 30$: \quad $\left(-\infty, \dfrac{5}{2}\right) \cup (6, \infty)$}\)
\(\textsf{$y = - x^2 - 6x - 8$: \quad $\left(-\infty, -4\right) \cup (-2, \infty)$}\)
Step-by-step explanation:
A function is positive when it is above the x-axis, and negative when it is below the x-axis.
---------------------------------------------------------------------------------
Given quadratic equation:
\(y = 2x^2 - 17x + 30\)
Factor the equation:
\(\implies y = 2x^2 - 17x + 30\)
\(\implies y = 2x^2 - 5x-12x + 30\)
\(\implies y=x(2x-5)-6(2x-5)\)
\(\implies y=(x-6)(2x-5)\)
The x-intercepts of the parabola are when y = 0.
To find the x-intercepts, set each factor equal to zero and solve for x:
\(\implies x-6=0 \implies x=6\)
\(\implies 2x-5=0 \implies x=\dfrac{5}{2}\)
Therefore, the x-intercepts are x = ⁵/₂ and x = 6.
The leading coefficient of the given function is positive, so the parabola opens upwards.
The function is positive when it is above the x-axis.
Therefore, the function is positive for the values of x less than the smallest x-intercept and more than the largest x-intercept:
\(\textsf{Solution: \quad $x < \dfrac{5}{2}$ \;and \;$x > 6$}\)\(\textsf{Interval notation: \quad $\left(-\infty, \dfrac{5}{2}\right) \cup (6, \infty)$}\)---------------------------------------------------------------------------------
Given quadratic equation:
\(y = - x^2 - 6x - 8\)
Factor the equation:
\(\implies y = - x^2 - 6x - 8\)
\(\implies y = -(x^2 +6x +8)\)
\(\implies y = -(x^2 +4x +2x+8)\)
\(\implies y = -((x(x+4)+2(x+4))\)
\(\implies y = -(x+4)(x+2)\)
The x-intercepts of the parabola are when y = 0.
To find the x-intercepts, set each factor equal to zero and solve for x:
\(\implies x+4=0 \implies x=-4\)
\(\implies x+2=0 \implies x=-2\)
Therefore, the x-intercepts are x = -4 and x = -2.
The leading coefficient of the given function is negative, so the parabola opens downwards.
The function is negative when it is below the x-axis.
Therefore, the function is negative for the values of x less than the smallest x-intercept and more than the largest x-intercept:
\(\textsf{Solution: \quad $x < -4$ \;and \;$x > -2$}\)\(\textsf{Interval notation: \quad $\left(-\infty, -4\right) \cup (-2, \infty)$}\)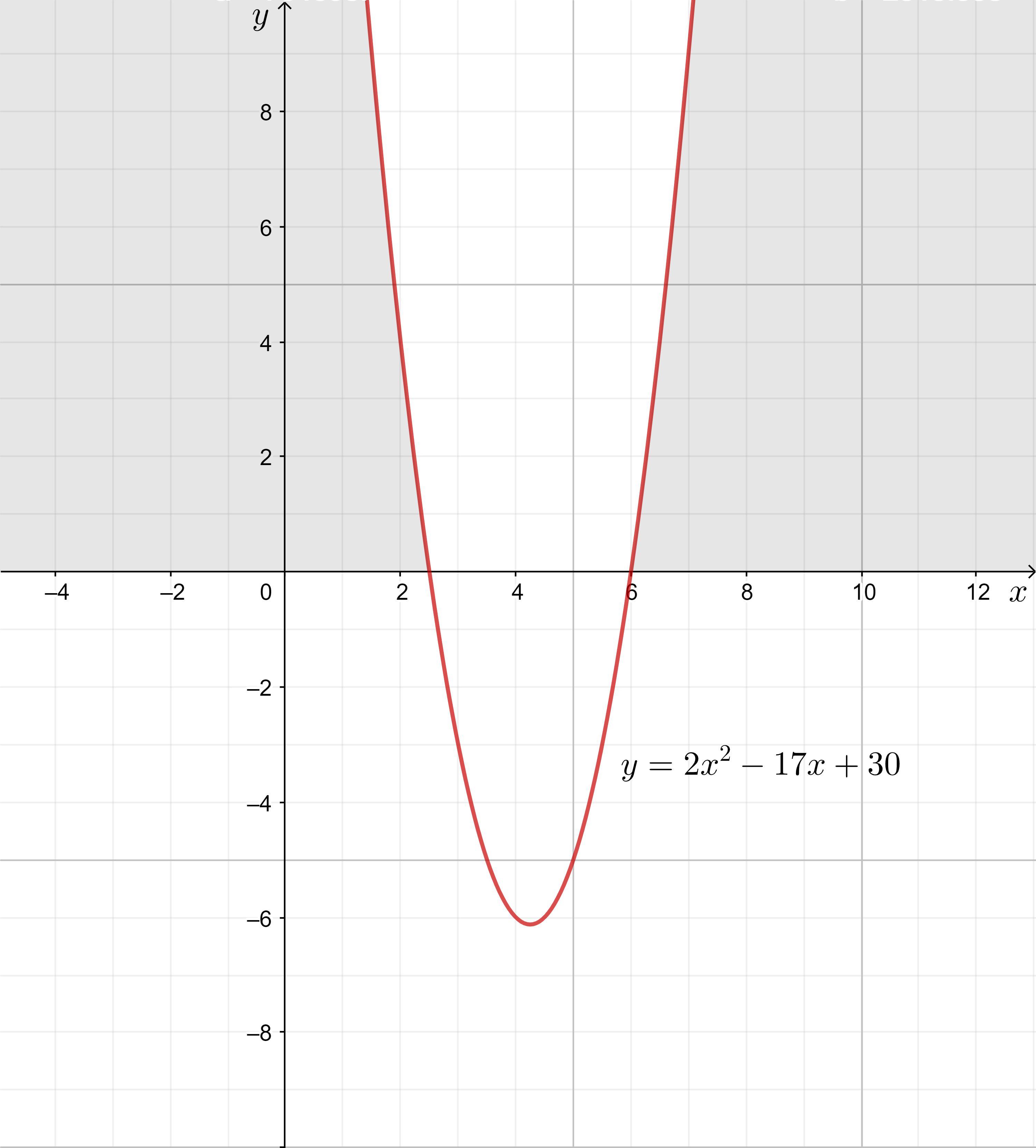

which elements in the following set are integers -8,3/4,-0.18,0,0.16,5,-2/7,6
Answers
Answer:
345
Step-by-step explanation:
A bag contains 3 blue marbles, 10 green marbles, 4 yellow marbles, and 8 red marbles. A marble is chosen at random, not replaced, then another marble is chosen. What is the probability that it is a red marble, then a blue marble? Write your answer as a fraction in simplest form.
Answers
Answer:
There are a total of 25 marbles in the bag.
The probability of choosing a red marble first is 8/25 since there are 8 red marbles out of 25 marbles in the bag.
Since a marble is not replaced after the first selection, there are now 24 marbles in the bag. There are still 3 blue marbles in the bag.
The probability of choosing a blue marble second, after a red marble has already been selected, is 3/24 or 1/8 since there are 3 blue marbles left out of 24 marbles in the bag.
To find the probability of both events occurring together, we multiply their individual probabilities:
8/25 x 1/8 = 1/25
Therefore, the probability that a red marble is chosen first, followed by a blue marble, is 1/25.
ASAP AND WILL GIVE BRAINLIEST
What is the range of the function y = e4*?
O y <0
O y > 0
O y <4
O y > 4

Answers
Answer:
y > 0
Step-by-step explanation:
\(y = e^{4x}\)
This is an exponential function;
Consider as x → ∞, y → ∞;
If x = 0. y = e⁰ = 1;
As x → -∞, y → 0;
y ranges from 0 to ∞ therefore, i.e. y > 0
Find the volume of this sphere.
Use 3 for T.
d=6in
V ~ [?]in3
V = Tr3
![Find the volume of this sphere.Use 3 for T.d=6inV ~ [?]in3V = Tr3](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/hMqymRLuuQiGIZsDQw73uYcWN2DK5eOI.png)
Answers
Answer:
V = 108 in³
Step-by-step explanation:
Given:
Volume of sphere = ⁴/3πr³
π = 3
d = 6 in.
r = ½(6) = 3 in.
Required:
Volume of sphere
Solution:
V = ⁴/3πr³
Plug in the values
V = ⁴/3 * 3 * 3³
V = ⁴/3 * 3 * 27
V = 4 * 27
V = 108 in³
look at the screenshot x

Answers
Answer:
31.01
Step-by-step explanation:
A= πr^2= π · 3.142 ≈31.01432
ANSWER CORRECT FOR BRAINLIEST - 10 POINTS
Which step in the software development life cycle analyzes the scope of work?
Coding
Design
Planning & Analysis
Testing
Answers
Simplify the following expression:
√-36+√-100+ 7
O A. 7+ 16i
OB. 7+√136i
O C. 16
C. 16 - 7i
O D. 23 + 0i
Answers
√-36 + √-100 + 7
To simplify this expression, we need to first remove the negative radicals. We can do this by squaring both sides of the equation:
√-36 = -6
√-100 = -10
Substituting these values back into the expression, we get:
-6 + -10 + 7 = -19 + 7 = -12
So, the simplified expression is:
-12
Since the expression is already in its simplified form, there is no need to factor it further.
If the area of a rectangle was 30m square and the length was 10m what is the perimeter of the rectangle
Answers
Answer:
26
Step-by-step explanation:
10*3 is 30, so 10+10+3+3
PLEASE HELP
Two projectiles are shot vertically upward at the same instant.
Projectile A's height in feet, f(t), is represented in the table, where t is the seconds since the projectile was shot off
Projectile B's height at any time t is modeled by the function
h (t)=-16t^2 +96t
How do the times at which the projectiles begin their descents compare?
SEE PHOTO

Answers
Projectile B begins its descent 1 seconds before Projectile A does.
What is y-intercept?In Mathematics and Geometry, the y-intercept of any graph or table such as a quadratic equation or function, generally occurs at the point where the value of "x" is equal to zero (x = 0).
By critically observing the table shown in the image attached above, we can reasonably infer and logically deduce the following y-intercept of Projectile A:
y-intercept = (0, 44).
Maximum height = (4, 300).
When t = 0, the y-intercept of Projectile B can be calculated as follows;
h(t) = -16t² + 96t
h(0) = -16(0)² + 96(0)
h(0) = 0.
For the maximum height, we have:
h(t) = -16t² + 96t
h'(t) = -32t + 96
32t = 96
t = 96/32
t = 3
Difference in time = 4 - 3
Difference in time = 1 seconds.
Read more on time and maximum height here: https://brainly.com/question/30145152
#SPJ1
Caroline can ride her bike 5 miles in 25 minutes. At this rate, how long would it take her to bike 8 miles?
Answers
Answer:
40 min.
Step-by-step explanation:
5/25=1/5
1/5=0.2
8/0.2=40
Answer:
40 mins
Step-by-step explanation:
do 25 divided by 5 and you get 5, which means she can ride one mile in 5 mins, so then multiply 5 and 8 and you get the product of 40.
