what is the length of the diagnal of a cube with a side length of 5 cm
Answers
Answer:
d≈8.66cm
Step-by-step explanation:
Related Questions
imagine you are on a game show. in front of you there are ten boxes, one of which contains a prize. you do not know which box contains the prize, but you are allowed to ask the game show host any number of yes-or-no questions to determine its position. however, you must submit these questions ahead of time, and the host will answer your questions in a random order so that you do not know which answer corresponds to which question. what is the fewest number of questions you can ask to ensure you can determine the position of the prize? what are these questions?
Answers
The questions are:
Is the prize in the first five boxes?
Is the prize in the first two and a half boxes?
Is the prize in the first or second box?
To find the prize with the fewest number of questions, we can use the binary search algorithm.
The algorithm works as follows:
Ask if the prize is in the first five boxes or the last five boxes.
Based on the answer, eliminate half of the boxes from consideration.
Repeat this process until only one box remains.
The fewest number of questions you can ask is log base 2 of the number of boxes, which in this case is log base 2 of 10, or approximately 3 questions.
The questions are:
Is the prize in the first five boxes?
Is the prize in the first two and a half boxes?
Is the prize in the first or second box?
Note that the exact wording of the questions may differ depending on the specific rules of the game show, but the principle remains the same.
For more questions on binary search algorithm
https://brainly.com/question/15190740
#SPJ4
Santana has already downloaded 8 songs and will continue to download 3 songs per hour.
Answers
EX:
1st: 11
2nd: 14
3rd: 17
4th: 20
5: 23
So on…
A linen service is delivering clean tablecloths to restaurants on its list of clients. A delivery is made to a restaurant in Oak Grove and then another in Newberry. On a map, these two are 9 inches apart; in real life, the distance is 3 miles. What is the map's scale?Use integer numbers.
Answers
To find the map's scale, use the formula below:
\(\text{map scale = }\frac{\text{ map distance}}{\text{ distance on the ground}}\)In this exercise,
map distane = 9 inches
distance on the ground = 3 miles.
So, the map scale is:
\(\begin{gathered} \text{map scale = }\frac{\text{9 inches}}{\text{ 3 miles}} \\ \end{gathered}\)Dividing both numerator and denominator by 3:
\(\begin{gathered} \text{map scale = }\frac{\text{9/3 inches}}{\text{ 3/3 miles}} \\ \text{map scale = }\frac{3\text{ inches}}{\text{ 1 miles}} \end{gathered}\)The map scale is: 3 inches : 1 mile.
The price of a computer was decreased by 7% to £500. What was the price before the decrease? Give your answer to the nearest penny.
Answers
Answer:
537.64
Step-by-step explanation:
some things you can put as notes for fitness
Answers
Here are some suggestions:
The exercise you're doing.
How frequent are you exercising.
The duration of exercise.
Fitness goals.
Location.
Time.
etc
Given the following formula, solve for I.
P = 2(1 + b)
A
P - 0
4
OB. 1 = 4(P + b)
= P =
P - 26
OD. I =P
P – 5
OC. 1 =
2

Answers
answer: c. l =p-2b/2
step by step:
p=2(1-b)
p=2l-2b
p+2b/2=2l/2
l =p-2b/2
A variable, other than the independent variable, that appears to have influenced the dependent variable in a study is referred to as Question 2 options: a covariate. an extraneous variable. a redundant variable. an inverse bias.
Answers
In research studies, an extraneous variable refers to a variable other than the independent variable that seems to have influenced the dependent variable.
These variables are sometimes also called "confounding variables" as they can create confusion or distortion in the relationship between the independent and dependent variables.
Extraneous variables can arise due to various factors such as measurement errors, participant characteristics, or environmental conditions. They have the potential to introduce bias and obscure the true effect of the independent variable on the dependent variable. To ensure accurate and valid results, researchers need to identify and control for these extraneous variables.
One common approach is to use statistical techniques such as regression analysis to account for the effects of extraneous variables by including them as covariates in the analysis. By doing so, researchers can isolate the specific impact of the independent variable on the dependent variable, while holding constant the influence of extraneous variables.
Overall, recognizing and managing extraneous variables is crucial in research to establish a clear cause-and-effect relationship between the independent and dependent variables and enhance the internal validity of the study.
Learn more about dependent variable here:
https://brainly.com/question/29430246
#SPJ11
Which of the following statements is true?
The probability of the union of two events can exceed one.
When events A and B are mutually exclusive, then P(A intersection b) = P(A) + P(B).
The union of events A and B consists of all outcomes in the sample space that are contained in both event A and B.
When two events A and B are independent, the joint probability of the events can be found by multiplying the probabilities of the individual events
Answers
The statement "When two events A and B are independent, the joint probability of the events can be found by multiplying the probabilities of the individual events" is true.
When two events A and B are independent, it means that the occurrence of one event does not affect the probability of the other event. In such cases, the joint probability of both events can be found by multiplying their individual probabilities. Mathematically, this can be expressed as P(A ∩ B) = P(A) * P(B). This rule holds true for independent events and is a fundamental concept in probability theory.
Now, let's examine the other statements:
1. The probability of the union of two events can exceed one:
This statement is false. The probability of an event is always between 0 and 1, inclusive. When you consider the union of two events, the probability of their combined occurrence cannot exceed 1. It is possible for the sum of the individual probabilities of the two events to exceed 1, but the probability of their union will never be greater than 1.
2. When events A and B are mutually exclusive, then P(A ∩ B) = P(A) + P(B):
This statement is false. Mutually exclusive events are events that cannot occur at the same time. If events A and B are mutually exclusive, their intersection (A ∩ B) will be an empty set, and therefore, the probability of their intersection is 0 (P(A ∩ B) = 0). The correct statement for mutually exclusive events is P(A ∪ B) = P(A) + P(B), where P(A ∪ B) represents the probability of the union of events A and B.
3. The union of events A and B consists of all outcomes in the sample space that are contained in both event A and B:
This statement is false. The union of events A and B, denoted as A ∪ B, consists of all outcomes that belong to either event A or event B or both. In other words, it includes all outcomes that are in A, in B, or in both A and B. The intersection of events A and B (A ∩ B) represents the outcomes that are contained in both A and B.
Learn more about joint probability here:
brainly.com/question/30224798
#SPJ11
HELP 15 POINTS
Write a rule for the nth term of the sequence. Then find a20 -
51,48,45,42

Answers
Answer:
45 because it is what I think
Find X
1. (10 marks) \( A=\left(\begin{array}{cc}2 & 1 \\ -4 & -3\end{array}\right) \) and \( B=\left(\begin{array}{ll}2 & 2 \\ 6 & 4\end{array}\right) \), find \( X \) so that \( A X=B \).
Answers
To find \(\(X\)\) such that \(\(AX = B\)\), where \(\(A\) and \(B\)\) are given matrices, we can use the formula \(\(X = A^{-1}B\), where \(A^{-1}\)\) represents the inverse of matrix \(\(A\)\).
To find \(\(X\)\), we need to multiply matrix \(\(A\) with \(X\)\) such that the result is matrix \(\(B\)\). In other words, we are looking for a matrix \(\(X\)\) that satisfies the equation \(\(AX = B\)\).
To solve this equation, we can multiply both sides by the inverse of matrix \(\(A\)\). The inverse of a matrix \(\(A\)\) is denoted as \(\(A^{-1}\)\) and has the property that \(\(A^{-1}A = I\)\), where \(\(I\)\) is the identity matrix.
By multiplying both sides of the equation \(\(AX = B\) by \(A^{-1}\)\)0
\(\(A^{-1}(AX) = A^{-1}B\)\)
Since \(\(A^{-1}A = I\)\), the left side simplifies to:
\(\(I(X) = A^{-1}B\)\)
Therefore, we have:
\(\(X = A^{-1}B\)\)
By evaluating the matrices \(\(A\) and \(B\)\) and finding the inverse of matrix \(\(A\)\), we can perform the matrix multiplication to find the value of \(\(X\)\) that satisfies the equation \(\(AX = B\)\).
Learn more about matrices here:
https://brainly.com/question/30646566
#SPJ11
A distribution is given as X ~ Exp(0. 75). Find P(x < 4)
Answers
The probability of P(x < 4) is 0.6922 or approximately 69.22%.
The exponential distribution is often used to model the time between events that occur randomly and independently at a constant rate over time. The probability density function of the exponential distribution with parameter λ is given by f(x) = λe^(-λx) for x ≥ 0.
In this case, X ~ Exp(0.75) means that the parameter λ is 0.75. To find P(x < 4), we need to calculate the area under the curve of the probability density function to the left of 4. This can be done by integrating the function from 0 to 4 as follows
P(x < 4) = ∫₀⁴ λe^(-λx) dx
= [-e^(-λx)]₀⁴
= -e^(-0.75 * 4) + 1
= 0.6922
Therefore, the probability that X is less than 4 is 0.6922 or approximately 69.22%.
To know more about probability here
https://brainly.com/question/31493532
#SPJ4
Home plate for professional baseball has the dimensions shown below. What is the area of home plate, in square inches?
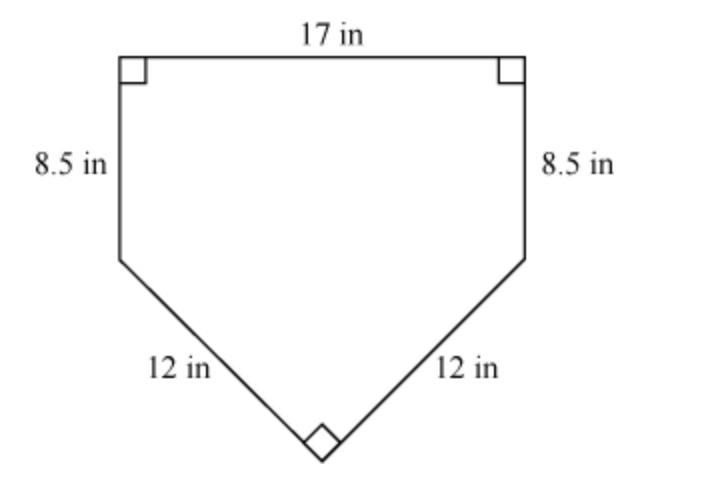
Answers
Answer:
Hi! The answer to your question is 176,868 Square Inches
Step-by-step explanation:
\(Area = Length * Width\)
\(8.5 * 12 * 12 *8.5 * 17 = 176,868\)
☆*: .。.。.:*☆☆.*: .。..。.:*☆☆*: .。.。.:*☆☆.*: .。..。.:*☆
☁Brainliest is greatly appreciated!☁
Hope this helps!!
- Brooklynn Deka
HI I really need help with this its in the picture

Answers
Explanation:
The blue rectangle has area of 4a^2*6a^2 = 24a^4
The red rectangle has area 4a^2*9a = 36a^3
The green rectangle has area 4a^2*3 = 12a^2
The total area is 24a^4 + 36a^3 + 12a^2
suppose that the lifetime of a transistor is a gamma random variable x with mean of 24 weeks and standard deviation of 12 weeks. what is the probability that the transistor will last between 12 and 24 weeks?
Answers
The probability that the transistor will last between 12 and 24 weeks is 0.424
X= lifetime of the transistor in weeks E(X)= 24 weeks
O,= 12 weeks
The anticipated value, variance, and distribution of the random variable X were all provided to us. Finding the parameters alpha and beta is necessary before we can discover the solutions to the difficulties.
X~gamma(\(\alpha ,\beta\))
E(X)= \(\alpha \beta\) \(\beta\)= \(12^{2}/24\)=6 weeks
V(x)= \(\alpha \beta ^{2}\) \(\alpha\)=24/6= 4
Now we can find the solutions:
The excel formula used to create Figure one is as follows:
=gammadist(X, \(\alpha\), \(\beta\), False)
P(\(12\leq X\leq 24\))
P(\(12/6\leq G\leq 24/6\))
P(\(2\leq G\leq 4\))
P= 0.424
Therefore, probability that the transistor will last between 12 and 24 weeks is 0.424
To learn more about probability click here:
brainly.com/question/11234923
#SPJ4
Answer:
Step-by-step explanation:
0.424 is the probability that the transistor will last between 12 and 24 weeks.
X= lifetime of the transistor in weeks E(X)= 24 weeks
Standard deviation= 12 weeks
Finding the parameters alpha and beta X~gamma(αβ)
E(X)= αβ β =6 weeks
V(x)=αβ^2 α =24/6= 4
Now we can find the solutions:
The excel formula used to create Figure one is as follows:
=gammadist(X,α,β,False)
P(12≤X≤24)
P(12/6≤G≤24/6)
P= 0.424
Therefore, probability that the transistor will last between 12 and 24 weeks is 0.424
To learn more about probability click here:
https://brainly.com/question/28944433
#SPJ4
The probability distribution histogram shows the number of trees in yards in a certain neighborhood.
What is the probability that a randomly selected yard will have 6 or more trees?

Answers
Answer:
45%
Step-by-step explanation:
Here, we want to know the probability of a randomly selected yard having 6 or more than 6 trees
To get this, we simply add up the probability of 6 yards and above
That is the probability of 6, 8 , 10 and 12 yards
This is obtainable from the histogram
We then proceed to add up from the graph
What we have is;
0.05 + 0.25 + 0.10 + 0.05
= 0.10 + 0.10 + 0.25 = 0.45
This is same as 45/100 which is otherwise 45%
The probability that a randomly selected yard will have 6 or more trees is 45%.
Probability of having 0-2 tree = 0.35
Probability of having 2-4 tree = 0.20
Probability of having 4-6 tree = 0.05
Probability of having 6-8 tree = 0.20
Probability of having 8-10 tree = 0.10
Probability of having 10-12 tree = 0.05
What is the probability?Probability is to quantify the possibilities or chances.
So, probability of having 6 or more trees
= (2*0.05 + 2*0.25 + 2*0.10 + 2*0.05)/(0.35*2+0.20*2+2*0.05 + 2*0.25 + 2*0.10 + 2*0.05)
=0.9/2
=0.45
=45%
So, probability of having 6 or more trees =45%
Therefore, the probability that a randomly selected yard will have 6 or more trees is 45%.
To get more about probability visit:
https://brainly.com/question/24756209
1. What is the prime factorization of 402? *
Your answer
Answers
Answer:
Step-by-step explanation:
Prime factorization requires dividing by primes starting with smallest prime number
402/2=201
201/3=67, 67 is prime so we cannot go further so the prime factorization of 402 is
2X3X67
a population of scores has µ = 80. in this population, a score of x = 86 corresponds to z = 2.00. what is the population standard deviation?
Answers
A population of scores has µ = 80. in this population, a score of x = 86 corresponds to z = 2.00. The population standard deviation is 03.
In statistics, the standard deviation is a measure of the variability or spread of an outcome. [1] A low standard deviation indicates that the value is close to the mean of the cluster (also called the expected value), while a high standard deviation indicates that the results are very interesting.
The standard deviation can be abbreviated as SD and is often used in mathematics and equations with the Greek letter σ (sigma) for population standard deviation or the Latin letter s for different sample sizes.
The standard deviation of a variable, such as a population, a data set, or a probability, is the basis of its variance. Algebraically it is easier than the mean absolute difference, but in practice, it is lower than the mean absolute difference. The useful feature of standard deviation is that it is expressed in the same unit as the data, unlike the difference.
Here we can use the Z-score formula:
Z = (X - µ) / σ
where Z is the Z-score, X is the individual score, µ is the population mean, and σ is the population standard deviation. In this case, we are given Z = 2.00, X = 86, and µ = 80. We need to find σ.
2.00 = (86 - 80) / σ
Now, solve for σ:
σ = (86 - 80) / 2.00 = 6 / 2.00 = 3
The population standard deviation (σ) is 3.
Learn more about Standard Deviation:
brainly.com/question/23907081
#SPJ11
Can someone help me find the property tax? I've tried the formulas my teacher gave me and they arent working. Please help.


Answers
Answer:
see attached
Step-by-step explanation:
The formulas given work perfectly.
It might help you to think of the tax rate as a percentage. For example, $2.37 per $100 is a rate of 2.37/100 = 0.0237 = 2.37%
Each dollar value is the product of the previous two columns.
$400,000 × 0.19 = $76,000; $76,000 × 0.0237 = $1801.20 (tax)
$235,000 × 0.10 = $23,500; $23,500 × 0.0993 = $2333.55 (tax)
$215,000 × 0.15 = $32,250; $32,250 × 0.1240 = $4000.00 (tax)
__
Where the rates are missing (as on the third line), they can be found by dividing the dollar value on the right of it by the dollar value on the left of it.
32,250/215,000 = 0.15 = 15%
4000/32,250 = 0.1240 = $12.40 per $100
_____
Additional comment
To get a tax of exactly $4000 on the last line, the tax rate needs to be specified to 4 decimal places: $12.4031 per $100. Otherwise the value rounds to something less than $4000.

A particle is described by the normalized wave function (x, y, z) = = Ae¯a(z²+y² +2²) where A and a are real positive constants. (a) Determine the probability of finding the particle at a distance between r and r+dr from the origin. Hint: use the volume of the spherical shell centered on the origin with inner radius r and thickness dr. (b) Calculate value of r at which the probability in part (a) have its maximum value. Is this the same value of r for which y(x, y, z)|² is a maximum? Explain any differences
Answers
(a) To determine the probability of finding the particle at a distance between r and r+dr from the origin, we need to calculate the volume of the spherical shell centered at the origin with an inner radius of r and a thickness of dr.
The volume of a spherical shell can be calculated as V = 4πr²dr, where r is the radius and dr is the thickness.
In this case, the wave function is given as (x, y, z) = Ae^(-a(z²+y²+x²)), and we need to find the probability density function |ψ(x, y, z)|².
|ψ(x, y, z)|² = |Ae^(-a(z²+y²+x²))|²
= |A|²e^(-2a(z²+y²+x²))
To find the probability of finding the particle at a distance between r and r+dr from the origin, we need to integrate |ψ(x, y, z)|² over the volume of the spherical shell.
P(r) = ∫∫∫ |ψ(x, y, z)|² dV
= ∫∫∫ |A|²e^(-2a(z²+y²+x²)) dV
Since the wave function is spherically symmetric, the integral simplifies to:
P(r) = 4π ∫∫∫ |A|²\(e^{-2a}\)(r²)) r² sin(θ) dr dθ dφ
Integrating over the appropriate ranges for r, θ, and φ will give us the probability of finding the particle at a distance between r and r+dr from the origin.
(b) To find the value of r at which the probability in part (a) has its maximum value, we can differentiate P(r) with respect to r and set it equal to zero:
dP(r)/dr = 0
Solving this equation will give us the value of r at which the probability has a maximum.
However, the value of r at which the probability has a maximum may not be the same as the value of r for which |ψ(x, y, z)|² is a maximum. This is because the probability density function is influenced by the absolute square of the wave function, but it also takes into account the volume element and the integration over the spherical shell. So, while the maximum value of |ψ(x, y, z)|² may occur at a certain r, the maximum probability may occur at a different r due to the integration over the spherical shell.
To know more about equation visit:
brainly.com/question/29538993
#SPJ11
What property of adaptive immunity allows a person to have the chicken pox when he or she is six years old and still be immune to chicken pox at age 45?
Answers
The property of adaptive immunity enables a person to have the chicken pox when he or she is six years old and still be immune to chicken pox at age 45 exists Memory.
What is adaptive immunity?Specificity and memory are two crucial properties that determine adaptive immunity. Both specificity and memory pertain to the adaptive immune system's capacity to recognize and attack certain diseases, as well as to promptly react to pathogens to which it has already been exposed.
Adaptive immunity can offer an enduring defense, perhaps for the duration of a person's lifespan. In certain circumstances, such as with chickenpox, it does not confer permanent protection; for instance, a person who recovers from measles is now protected against measles for the rest of their life.
Specificity, diversity, specialization, memory, and self/non-self identification are the immunologic characteristics that define adaptive immunity, and these cells both create and show antigen-binding cell surface receptors.
The property of adaptive immunity enables a person to have the chicken pox when he or she is six years old and still be immune to chicken pox at age 45 exists Memory.
To learn more about adaptive immunity refer to:
https://brainly.com/question/15446299
#SPJ4
Please hellp
(05.02)A farmer has decided to divide his land area in half in order to plant soy and corn. Calculate the area of the entire area so he knows how much soil is needed.
A parallelogram with a height of 6 yards and side length 9 yards. The height forms a triangle with the slanted side of the rhombus with a base of 2.5 yards. Rhombus is split into a soy half and a corn half.
Each bag of soil covers 40 square yards. How many bags should the farmer purchase?
1 bag
2 bags
3 bags
4 bags
Answers
Answer:
he needs 3 bags i did this test
Step-by-step explanation:
Answer:
3
Step-by-step explanation:
Jenny invests £8500 for 3 years in a savings account. She gets 2.3% per year simple interest. (this is where you calculate the profit for ONE year and just add it on... NOT compound interest) How much money will Jenny have in her savings account at the end of 3 years?
Answers
Answer:
£9095
Step-by-step explanation:
Given data
P=£8500
T= 3 years
R= 2.3%
The compound interest formula is
A= P(1+r)^t
substitute
A=8500(1+0.023)^3
A=8500(1.023)^3
A=8500*1.07
A=£9095
Hence the savings after 3 years is £9095
Зу + 5.2 = 2- 5y
What is the answer for this??

Answers
8y = 7.2
Y = 0.9
Answer:
The answer is y=0.4
Evaluate the expression using a calculator. Round your answer to two decimal places when appropriate.
Square root 5^32,768 =

Answers
The value of the equation is A = ⁵√32,768 is A = 8
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Substituting the values in the equation , we get
A = ⁵√32,768 be equation (1)
On simplifying the equation , we get
A = 8 x 8 x 8 x 8 x 8 = 32,768
So , the 5th root of ( 32,768 ) is 8
Therefore , the value of A = 8
Hence , the equation is A = 8
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
The point (-5,-4)
is rotated 90
counterclockwise .
Answers
Answer:
4,5
Step-by-step explanation:
I hope this helps
Make r the subject of the formula t = r
_
r - 3

Answers
We will try to leave the letter \(r\) alone by modifying the given equation.
\(t=\frac{r}{r-3}\)\(\frac{1}{t}=\frac{r-3}{r}\)\(\frac{1}{t}=1-\frac{3}{r}\)\(\frac{1}{t}-1=-\frac{3}{r}\)\(1-\frac{1}{t}=\frac{3}{r}\)\(\frac{1}{3}-\frac{1}{3t}=\frac{1}{r}\)\((\frac{t-1}{3t} )^{-1}=(\frac{1}{r} )^{-1}\)\(\frac{3t}{t-1}=r\)This equation is defined with the following expressions.
\(t\neq 1\)\(r\neq 3\)Ans: \(r=\frac{3t}{t-1}\)
-
?% of $8,000,000 = $1,600,000
Answers
Answer:
20%
Step-by-step explanation:
To solve, we can calculate how much 1,600,000 is of 8,000,000 as a decimal and then solve from there.
Let's say our missing value is x.
x of 8,000,000 = 1,600,000
"x of something", in this case, can be rephrased as "x * something", so we have
x * 8,000,000 = 1,600,000
divide both sides by 8,000,000 to isolate x
x = 1,600,000/8,000,000 = 0.2
to convert from a decimal to percentage, multiply by 100
0.2 * 100 = 20
20% is our answer
Can you help plss and thank you

Answers
Answer:
Step-by-step explanation:
The area formula for a parallelogram is the same as the area formula for a rectangle or square. A = bh.
Our base is 5 1/4 and the height, which drops perpendicular to the base, is 4 1/5. So the formula for the area is
\(A=(4\frac{1}{5})(5\frac{1}{4})\)
Choice D
Two players each flip a fair coin. The probability that they get the same result can be expressed as ab where a and b are coprime positive integers.
What is the value of a+b ?
Answers
There are four outcomes that can occur when two players flip fair coins: both coins must be heads (HH), both must be tails (TT), or one coin must be heads and the other must be tails (HT or TH).
Because these are the only outcomes in which both players receive the same outcome, the probability that they will have the same outcome is equal to the sum of the probabilities of getting HH and TT. The likelihood of receiving HH or TT is:
HH or TT, where P(HH) = P(HH) + P(TT) = 1/4 + 1/4 = 1/2
As a result, the likelihood that they arrive at the same conclusion can be expressed as 1/2, a fraction with a coprime denominator and numerator.
As a result, a+b has the value:
a + b = 1 + 2 = 3
So, the response is 3.
To Learn More About probability click
https://brainly.com/question/11234923
#SPJ4
through: (-4,-3), parallel to y=2x+4
Whts this in slope int form

Answers
Answer:
y=2(x+4)-3
Step-by-step explanation:
To make it parallel to y=2x+4, the slope needs to be the same
Point-slope form is: y=m(x-x1)+y1
In this case,
m = 2
x1 = -4
y1 = -3
So when put into point-slope form, it is y=2(x+4)-3