What expression in terms of x can be used to represent the area of parallelogram PQRS?

Answers
Answer:
C. (5x√2)² = 50x²
Step-by-step explanation:
Area of parallelogram = QR²
QR = √((5x)² + (5x)²) ---› pythagorean theorem
QR = √(25x² + 25x²) =
QR = √(50x²)
QR = √(25*2*x²)
QR = 5x√2
✔️Area of parallelogram = QR²
= (5x√2)² = 25x² × 2 = 50x²
Related Questions
the length of a basketball pitch can be divided into 12 parts which 25 centimetres on how much parts it's 20 centimetres long can be obtained from the pitch
Answers
Answer:
the number of parts is going to be
= 15 parts
Step-by-step explanation:
A basketball pitch can be divided into twelve(12) parts , each part of equal length of twenty five (25) centimeters.
The initial and total length of the basketball pitch = 12*25
The initial and total length of the basketball pitch = 12*25
The initial and total length of the basketball pitch = 300 cm
So if it's now divided into parts of each 20 cm ,
the number of parts is going to be
= 300/20
the number of parts is going to be
= 15 parts
(ALREADY ANSWERED) Which system of inequalities represents the graph?
Responses
⎧⎩⎨⎪⎪3x+5y≥10−x+y<−5y−6<−5x
First inequality. 3 x plus 5 y greater than or equal to 10. Second inequality. negative x plus y less than negative 5. Third inequality. y minus 6 less than negative 5 x.
⎧⎩⎨⎪⎪3x+5y≤10−x+y>−5y−6>−5x
First inequality. 3 x plus 5 y less than or equal to 10. Second inequality. negative x plus y greater than negative 5. Third inequality. y minus 6 greater than negative 5 x.
⎧⎩⎨⎪⎪5y−10≥−3xy+5>xy+5x>6
First inequality. 5 y minus 10 greater than or equal to negative 3 x. Second inequality. y plus 5 greater than x. Third inequality. y plus 5 x greater than 6.
⎧⎩⎨⎪⎪5y−10≤−3xy+5
First inequality. 5 y minus 10 less than or equal to negative 3 x. Second inequality. y plus 5 less than x. Third inequality. y plus 5 x less than 6.

Answers
After plotting the inequalities, we see that the second set satisfies the graph provided.
How can we graph inequalities?
A linear or quadratic inequality can be graphed in a manner similar to that of an equation. The distinction is that an inequality displays a range of values greater than or less than, thus your graph will display more than just a dot on a number line or a line on a coordinate plane. You can figure out which numbers are part of an inequality solution by utilizing algebra and evaluating the inequality sign.
Let the first inequality be \(3x+5y\leq 10\).
When we plot the equality, we see that it covers the portion including the origin.
Next inequality is \(-x+y > -5\).
When plotting this one, we again see that it covers the portion including the origin.
The last equality is \(y-6 > -5x\).
While plotting it, we see that this line overlaps the other 2 lines making a common space of the triangle that is shown in the figure.
Hence the second set of inequalities represent the graph.
To learn more about inequalities, visit the following link:
https://brainly.com/question/29227973
#SPJ1
After plotting the inequalities, we see that the second set satisfies the graph provided.
How can we graph inequalities?
To graph inequalities, you can use a number line or a coordinate plane. Here's an example of how to graph an inequality on a number line:
First, determine the inequality symbol: >, <, ≥, or ≤.
Next, determine the value of the inequality.
Plot the value on the number line, using an open circle for > or <, and a closed circle for ≥ or ≤.
Shade in the region on one side of the plotted point, according to the inequality symbol. For example, if the inequality is x > 3, then you would shade in the region to the right of 3, since values greater than 3 satisfy the inequality.
Here's an example of how to graph an inequality on a coordinate plane:
First, determine the inequality symbol: >, <, ≥, or ≤.
Next, rewrite the inequality in the form "y > f(x)" or "y < f(x)" by isolating the y term on one side of the inequality.
Plot the function f(x) on the coordinate plane.
Shade in the region above or below the plotted function, depending on the inequality symbol. For example, if the inequality is y > f(x), then you would shade in the region above the plotted function, since values of y greater than f(x) satisfy the inequality.
Let the first inequality be \(3x+5y\leq 10\)
When we plot the equality, we see that it covers the portion including the origin.
Next equality is \(-x+y > -5\)
When plotting this one, we again see that it covers the portion including the origin.
The last equality is \(y-6 > -5x\)
While plotting it, we see that this line overlaps the other 2 lines making a common space of the triangle that is shown in the figure.
Hence the second set of inequalities represent the graph.
To learn more about inequalities follow link:
https://brainly.com/question/29227973
#SPJ1
Question 2 For the following matrix Then [340]
A= [-127]
[-2-44]
(Please use a comma between two numbers.)
(a) The minors M13, M23, M33= 8,-4,10
(b)The cofactors C13, C23,C33= 8,4,10 (c) The determinant det(A) = 68
Answers
For the given matrix A, the minors M13, M23, M33 are 8, -4, and 10 respectively. The cofactors C13, C23, C33 are 8, 4, and 10 respectively. The determinant det(A) is 68.
To find the minors of a matrix, we need to find the determinants of the submatrices obtained by removing the row and column corresponding to the element of interest. In this case, the minors M13, M23, and M33 correspond to the determinants of the 2x2 submatrices obtained by removing the first row and the third column, second row and third column, and third row and third column, respectively.
To find the cofactors, we multiply each minor by a positive or negative sign based on its position in the matrix. The signs alternate starting with a positive sign for the top left element. In this case, the cofactors C13, C23, and C33 correspond to the minors M13, M23, and M33 respectively.
Finally, the determinant of a 3x3 matrix can be found by using the formula det(A) = a11C11 + a12C12 + a13C13, where a11, a12, and a13 are the elements of the first row of the matrix and C11, C12, and C13 are their corresponding cofactors. In this case, the determinant det(A) is 68.
Therefore, the minors M13, M23, M33 are 8, -4, and 10 respectively. The cofactors C13, C23, C33 are 8, 4, and 10 respectively. And the determinant det(A) is 68.
Learn more about submatrices here:
https://brainly.com/question/31669133
#SPJ11
what dose this mean :(me need to draw line

Answers
Because OP only asked for a clarification of the problem statement:
You are asked to find the green area. (Hint: divide the green area into rectangles and right triangles, because you know their area.)
A bridge hand contains 13 cards from a standard deck. Find the probability that a bridge hand will contain all 13 cards of the same suit. What The Flush !!!! a) 1/(52 13) b) 4/(52 13) c) 13/(52 13) d) (13 4) /(52 13)
Answers
The probability will be b) 4/(52 13)
In a standard deck, there are four suits (hearts, diamonds, clubs, and spades), each containing 13 cards. To find the probability of obtaining a bridge hand with all 13 cards of the same suit, we need to determine the number of favorable outcomes (hands with all 13 cards of the same suit) and divide it by the total number of possible outcomes (all possible bridge hands).
Calculate the number of favorable outcomes
There are four suits, so for each suit, we can choose 13 cards out of 13 in that suit. Therefore, there is only one favorable outcome for each suit.
Calculate the total number of possible outcomes
To determine the total number of possible bridge hands, we need to calculate the number of ways to choose 13 cards out of 52. This can be represented as "52 choose 13" or (52 13) using the combination formula.
Calculate the probability
The probability is given by the ratio of the number of favorable outcomes to the total number of possible outcomes. Since there is one favorable outcome for each suit and a total of 4 suits, the probability is 4 divided by the total number of possible outcomes.
Therefore, the probability that a bridge hand will contain all 13 cards of the same suit is 4/(52 13).
Learn more about probability
brainly.com/question/31828911
#SPJ11
Sally has three tiles each tile has a number on it sally puts the three tiles down to make a number each number is made with all three tiles how many different numbers can sally make
Answers
Answer:
6
Step-by-step explanation:
123
132
213
231
312
321
which totals to 6 overall combinations
1. (1 point) Let x be a real number. Show that a (1 + x)2n > 1+ 2nx for every positive integer n.
Answers
For a real number x, by using mathematical induction it is shown that a\((1 + x)^{2n}\) > 1 + 2nx for every positive integer n.
To prove the inequality a\((1 + x)^{2n}\) > 1 + 2nx for every positive integer n, we will use mathematical induction.
The inequality holds true for n = 1, and we will assume it is true for some positive integer k.
We will then show that it holds for k + 1, which will complete the proof.
For n = 1, the inequality becomes a\((1 + x)^2\) > 1 + 2x.
This can be expanded as a(1 + 2x + \(x^2\)) > 1 + 2x, which simplifies to a + 2ax + a\(x^2\) > 1 + 2x.
Now, let's assume the inequality holds true for some positive integer k, i.e., a\((1 + x)^{2k}\) > 1 + 2kx.
We need to prove that it holds for k + 1, i.e., a\((1 + x)^{2(k+1)}\) > 1 + 2(k+1)x.
Using the assumption, we have a\((1 + x)^{2k}\) > 1 + 2kx.
Multiplying both sides by \((1 + x)^2\), we get a\((1 + x)^{2k+2}\) > (1 + 2kx)\((1 + x)^2\).
Expanding the right side, we have a\((1 + x)^{2k+2}\) > 1 + 2kx + 2x + 2k\(x^2\) + 2\(x^2\).
Simplifying further, we get a\((1 + x)^{2k+2}\) > 1 + 2(k+1)x + 2k\(x^2\) + 2\(x^2\).
Since k and x are positive, 2k\(x^2\) and 2\(x^2\) are positive as well.
Therefore, we can write a\((1 + x)^{2k+2}\) > 1 + 2(k+1)x + 2k\(x^2\) + 2\(x^2\) > 1 + 2(k+1)x.
This proves that if the inequality holds for some positive integer k, it also holds for k + 1.
Since it holds for n = 1, it holds for all positive integers n by mathematical induction.
Therefore, we have shown that a\((1 + x)^{2n}\) > 1 + 2nx for every positive integer n.
Learn more about mathematical induction here:
https://brainly.com/question/29503103
#SPJ11
A fair six sided die (sides of 1,2,3,4,5, and 6, and each side is equally likely) is to be thrown 5 (five) times. The throws are independent of one another. What is the probability that you roll an even number in at least one of the throws
Answers
The probability of rolling an even number in at least one of the throws is 31/32 or approximately 0.969.
The probability of not rolling an even number in a single throw is 1/2, since there are three odd numbers and three even numbers on the die. Therefore, the probability of not rolling an even number in five independent throws is (1/2)^5 = 1/32.
The probability of rolling an even number in at least one of the throws is the complement of the probability of not rolling an even number in any of the five throws. So:
P(rolling an even number in at least one of the throws) = 1 - P(not rolling an even number in any of the five throws)
= 1 - (1/32)
= 31/32
Therefore, the probability of rolling an even number in at least one of the throws is 31/32 or approximately 0.969.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
3х + бу
бу =
18 and Зу = - 5х + 9
do these have one solution,ims,or no solution
Answers
Answer:
The solution of the system of equations will be:
\(x=0,\:y=3\)
And the system of equations has ONLY ONE solution.
Step-by-step explanation:
Given the system of the equations
\(\begin{bmatrix}3x+6y=18\\ 3y=-5x+9\end{bmatrix}\)
Arrange equation variables for elimination
\(\begin{bmatrix}3x+6y=18\\ 5x+3y=9\end{bmatrix}\)
\(\mathrm{Multiply\:}3x+6y=18\mathrm{\:by\:}5\:\mathrm{:}\:\quad \:15x+30y=90\)
\(\mathrm{Multiply\:}5x+3y=9\mathrm{\:by\:}3\:\mathrm{:}\:\quad \:15x+9y=27\)
\(\begin{bmatrix}15x+30y=90\\ 15x+9y=27\end{bmatrix}\)
\(15x+9y=27\)
\(-\)
\(\underline{15x+30y=90}\)
\(-21y=-63\)
so the system of the equations becomes
\(\begin{bmatrix}15x+30y=90\\ -21y=-63\end{bmatrix}\)
solve -21y = -63
\(-21y=-63\)
\(\mathrm{Divide\:both\:sides\:by\:}-21\)
\(\frac{-21y}{-21}=\frac{-63}{-21}\)
\(y=3\)
\(\mathrm{For\:}15x+30y=90\mathrm{\:plug\:in\:}y=3\)
\(15x+30\cdot \:3=90\)
\(15x+90=90\)
subtract 90 from both sides
\(15x+90-90=90-90\)
\(15x=0\)
Divide both sides by 15
\(\frac{15x}{15}=\frac{0}{15}\)
\(x = 0\)
as
\(x = 0\), \(y=3\)
so, the system of equations contains only one solution.
Therefore, the solution of the system of equations will be:
\(x=0,\:y=3\)
And the system of equations has ONLY ONE solution.
PRETEST: The Number System
What is the fractional equivalent of the repeating decimal 0.2?
0339
off
O
O
6/N
27
5 of 13 QUESTIONS
SUBMIT
Answers
The fractional equivalent of the repeating decimal 0.2 is 2/9
How to determine the fractional equivalent of the repeating decimalFrom the question, we have the following parameters that can be used in our computation:
Repeating decimal = 0.2
Represent properly
So, we have
Repeating decimal = 0.2222
Express as fraction
So, we have
Fraction = 2/(10 - n)
In this case
n = 1
So, we have
Fraction = 2/(10 - 1)
Evaluate
Fraction = 2/9
Hence, the fractional equivalent is 2/9
Read more about repeating decimal at
https://brainly.com/question/12407250
#SPJ1
What is the slope of the line that goes through the points (1, -5) and (4, 1)

Answers
Answer:
D) 2
Step-by-step explanation:
Use the following slope formula:
m (slope) = (y₂ - y₁)/(x₂ - x₁)
Let:
(x₁ , y₁) = (4 , 1)
(x₂ , y₂) = (1 , -5)
Plug in the corresponding numbers to the corresponding variables:
m = (-5 - 1)/(1 - 4)
Simplify. Remember to follow PEMDAS. First subtract, then divide:
m = (-5 - 1)/(1 - 4)
m = (-6)/(-3)
m = 2
D) 2 is your answer.
~
how would i write the x and y values
Answers
2. Find the length of the hypotenuse.
45°
3√2
Answers
The triangle is an isosceles right-angle triangle. Then the hypotenuse of the triangle will be 3 units.
What is a right-angle triangle?It's a form of a triangle with one 90-degree angle that follows Pythagoras' theorem and can be solved using the trigonometry function.
The measure of one angle of right-angle is 45°. Then the right triangle is an isosceles right-angle triangle.
Then the hypotenuse is given by the sine of angle 45°. Then the equation is given as,
sin 45° = 3√2 / H
1/√2 = 3√2 / H
H = 3√2 x (1 / √2)
H = 3 units
The triangle is an isosceles right-angle triangle. Then the hypotenuse of the triangle will be 3 units.
More about the right-angle triangle link is given below.
https://brainly.com/question/3770177
#SPJ9
Consider the given pseudo code. Write the function T(n) in terms of the number of operations, and then give the asymptotic (big Oh) complexity of the algorithm, show all the work you do. [ write the summation formula and solve it, or use the "Look for pattern"method. a. Matrix Multiplication
Answers
The function T(n) in terms of the number of operations is:
T(n) = 2n^3 + 3n^2 + 2n + 1 and the asymptotic complexity of the matrix multiplication algorithm is O(n^3).
To analyze the provided pseudo code for matrix multiplication and determine the function T(n) in terms of the number of operations, we need to examine the code and count the number of operations performed.
The pseudo code for matrix multiplication may look something like this:
```
MatrixMultiplication(A, B):
n = size of matrix A
C = empty matrix of size n x n
for i = 1 to n do:
for j = 1 to n do:
sum = 0
for k = 1 to n do:
sum = sum + A[i][k] * B[k][j]
C[i][j] = sum
return C
```
Let's break down the number of operations step by step:
1. Assigning the size of matrix A to variable n: 1 operation
2. Initializing an empty matrix C of size n x n: n^2 operations (for creating n x n elements)
3. Outer loop: for i = 1 to n
- Incrementing i: n operations
- Inner loop: for j = 1 to n
- Incrementing j: n^2 operations (since it is nested inside the outer loop)
- Initializing sum to 0: n^2 operations
- Innermost loop: for k = 1 to n
- Incrementing k: n^3 operations (since it is nested inside both the outer and inner loops)
- Performing the multiplication and addition: n^3 operations
- Assigning the result to C[i][j]: n^2 operations
- Assigning the value of sum to C[i][j]: n^2 operations
Total operations:
1 + n^2 + n + n^2 + n^3 + n^3 + n^2 + n^2 = 2n^3 + 3n^2 + 2n + 1
Therefore, the function T(n) in terms of the number of operations is:
T(n) = 2n^3 + 3n^2 + 2n + 1
To determine the asymptotic (big O) complexity of the algorithm, we focus on the dominant term as n approaches infinity.
In this case, the dominant term is 2n^3. Hence, the asymptotic complexity of the matrix multiplication algorithm is O(n^3).
To know more about asymptotic complexity refer here:
https://brainly.com/question/30214690#
#SPJ11
A researcher wants to test that the mean age of bus drivers in Chicago is 56.4 years old What are the appropriate nul and alternate hypotheses? O
A. H0= 58A, H1:mu < 56A B. H0. TU = 58A, H1:mu> 56A C. H0.mu.19.56A, H1 = 56A D. H0. = 56.A. H1mu.ne.56A
Answers
The appropriate nul and alternate hypotheses is option ( D) H0: μ = 56.4, H1: μ ≠ 56.4.
In hypothesis testing, the null hypothesis (H0) is the statement that there is no significant difference between the population parameter (in this case, the mean age of bus drivers in Chicago) and a specified value (in this case, 56.4 years old). The alternative hypothesis (H1) is the statement that there is a significant difference between the population parameter and the specified value.
The appropriate null and alternative hypotheses for the given scenario can be stated as follows
H0: μ = 56.4 (the population mean age of bus drivers in Chicago is 56.4 years old)
H1: μ ≠ 56.4 (the population mean age of bus drivers in Chicago is not equal to 56.4 years old)
Therefore, the correct option is (D) H0: μ = 56.4, H1: μ ≠ 56.4.
Learn more about hypothesis testing here
brainly.com/question/30588452
#SPJ4
Indicate below weather the equation in the box is true or false

Answers
Answer:
False
Step-by-step explanation:
4/8 equals to 1/2 but 6/10 equals to 3/5. Correct would be if it was 5/10
please help me!!!!!!!!!!!!!

Answers
Answer:
I'm not positive on this but I think the answer might be C 27 sin (39)/ sin (51)
Step-by-step explanation:
Write an equation of the line given

Answers
Slope is positive 2(up 2, right 1)
First point/ y intercept is -3
Answer: y=2x+1
Step-by-step explanation:
What is the solution set of (x-2)(x-3) = 2?
O (1.4)
O (2, 3)
O [4,5)
Answers
(1,4)
Answer:
I think A but i'm not sure
Step-by-step explanation:
Which ordered pair makes both inequalities true?
y > –3x + 3
y > 2x – 2
On a coordinate plane, 2 straight lines are shown. The first solid line has a positive slope and goes through (0, negative 2) and (1, 0). Everything to the left of the line is shaded. The second dashed line has a negative slope and goes through (0, 3) and (1, 0). Everything to the right of the line is shaded.
(1,0)
(–1,1)
(2,2)
(0,3)
Answers
Answer:
its (2,2)
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
solve the quadratic equation giving your answer to 3dp 3x^2+9x-10=0
please show workings out
Answers
Answer:
d= -1/px + 10/9px^2
Step-by-step explanation:

4. The quotient of x and 7 is 5 more than three times x.

Answers
Well,
it says The quatient of x and seven is 5 more than three times x
The quotient = x/7
three times x = 3x
x/7 = 3x + 5 This is the answer
Please help me solve the question from below. It is from IM3 Algebra

Answers
The equation log₂(x - 1) = x³ - 4x has one solution at x = 2.
To determine the solutions to the equation log₂(x - 1) = x³ - 4x, we can set the two expressions equal to each other:
log₂(x - 1) = x³ - 4x
Since we know that the graphs of the two functions intersect at the points (2, 0) and (1.1187, -3.075), we can substitute these values into the equation to find the solutions.
For the point (2, 0):
log₂(2 - 1) = 2³ - 4(2)
log₂(1) = 8 - 8
0 = 0
The equation holds true for the point (2, 0), so (2, 0) is one solution.
For the point (1.1187, -3.075):
log₂(1.1187 - 1) = (1.1187)³ - 4(1.1187)
log₂(0.1187) = 1.4013 - 4.4748
-3.075 = -3.0735 (approx.)
The equation is not satisfied for the point (1.1187, -3.075), so (1.1187, -3.075) is not a solution.
Therefore, the equation log₂(x - 1) = x³ - 4x has one solution at x = 2.
Learn more about Logarithm here:
https://brainly.com/question/30226560
#SPJ1
. adapt the bubble sort algorithm so that it stops when no interchanges are required. express this more efficient version of the algorithm in pseudocode.
Answers
Modification makes the algorithm more efficient because if the array is already sorted, it will exit the loop early without unnecessary iterations.
How can we determine algorithm ?
The efficient version of the bubble sort algorithm uses a boolean variable to check whether any interchanges have been made.
The modified Bubble Sort algorithm that stops when no interchanges are required:
1. Set n to be the size of the array
2. Repeat the following steps until no interchanges are required:
a. Set swapped to false
b. For i = 0 to n-2 do the following:
i. If array[i] > array[i+1] then swap array[i] and array[i+1], set swapped to true
c. If swapped is still false, then exit the loop
3. The sorted array is now in the original array
In this modified algorithm, we first set swapped to false, which indicates that no interchanges have been made yet. We then go through the array and compare each adjacent pair of elements.
If the elements are out of order, we swap them and set swapped to true to indicate that an interchange has been made.
If, after going through the entire array, no interchanges have been made (swapped is still false), we exit the loop, as the array is already sorted.
This modification makes the algorithm more efficient because if the array is already sorted, it will exit the loop early without unnecessary iterations.
Learn more about algorithm
brainly.com/question/22984934
#SPJ11
Write an expression for the cost per person if five friends share the cost of a dinner equally.
Answers
Answer:
Let c=cost of dinner, 5=the # of people, and P=the cost of person
P=C/5
b. P = (1000)/5
P = 200
Step-by-step explanation:
Find the equation of the line shown.

Answers
Answer:
y = mx + b
y = 1/4x + 2
Step-by-step explanation:
m(slope) = rise/run = 1/4
b(y intercept) = 2
find the value of x of triangle
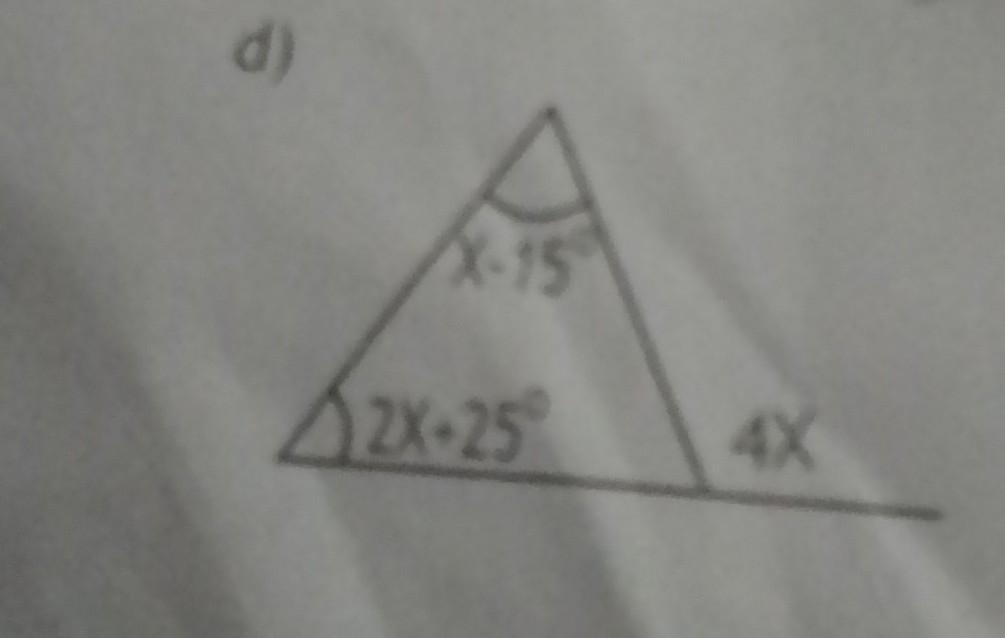
Answers
Answer:
By the math, x = 10°
Here's my issue though, the top angle is x - 15°. That would be an angle of -5° which is impossible.
Step-by-step explanation:
x - 15 + 2x + 25 + 180 - 4x = 180°
combine like terms:
3x - 4x + 190 = 180°
-x = -10°
x = 10°
Let V be the vector space of all real 2x2 matrices and let A = -(2) be the diagonal matrix. 0 Calculate the trace of the linear transformation L on V defined by L(X) = (AX + XA).
Answers
To calculate the trace of the linear transformation L on V defined by L(X) = (AX + XA), we need to find the matrix representation of L and then compute the sum of the diagonal elements of that matrix.
Let's start by expressing the matrix A and an arbitrary 2x2 matrix X:
A = [a b]
[c d]
X = [x1 x2]
[x3 x4]
Now, we can calculate AX and XA:
AX = [ax1 + bx3 ax2 + bx4]
[cx1 + dx3 cx2 + dx4]
XA = [x1a + x2c x1b + x2d]
[x3a + x4c x3b + x4d]
Adding AX and XA, we get:
AX + XA = [ax1 + bx3 + x1a + x2c ax2 + bx4 + x1b + x2d]
[cx1 + dx3 + x3a + x4c cx2 + dx4 + x3b + x4d]
Simplifying, we obtain:
AX + XA = [(2a + a)x1 + (b + 2c)x2 (a + 2b)x3 + (2d + c)x4]
[(c + 2d)x1 + (d + 2a)x2 (b + 2c)x3 + (c + 2d)x4]
The matrix representation of the linear transformation L is:
[2a + a b + 2c]
[c + 2d 2d + a]
Now, we can calculate the trace by summing the diagonal elements:
Trace(L) = (2a + a) + (2d + a)
= 3a + 2d
Therefore, the trace of the linear transformation L is 3a + 2d.
Learn more about linear here
https://brainly.com/question/2030026
#SPJ11
The blades of a windmill turn on an axis that is 35 feet above the ground. The blades are 10 feet long and complete two rotations every minute. Which of the following equations can be used to model h, the height in feet of the end of one blade, as a function of time, t, in seconds
Answers
The correct option is (c) h = 10sin(π15t)+35.
The equations can be used to model h, the height in feet of the end of one blade, as a function of time, t, in seconds is h = 10sin(π15t)+35.
How do windmills rotate?The blades of a turbine, which resemble propellers and function much like an airplane wing, capture the wind's energy.
A pocket of low-pressure air develops on one side of the blade when the wind blows. The blade is subsequently drawn toward the low-pressure air pocket, which turns the rotor.
Calculation for the equation of the model height-
Let's now review each choice individually and select the best one.
The blade is horizontal at time t = 0. As a result, h = 35 at t = 0 is valid for all of the possibilities in this situation.
They accomplish two spins in a minute. The blades will so complete one rotation in 30 seconds. and they will complete a quarter rotation in 15/2 seconds. Because of this, the blade will be vertically up from time t = 0 to t = 15/2. Its height in this instance should be 35 + 10 = 45 ft. Let's now examine the available possibilities.
If we put t=15/2 in the options
Option (a) gives h = 25
Option (b) gives h = -10sin(15/2) + 35
Option (c) gives h = 45
Option (d) gives h = 10sin(15/2) + 35
Therefore, the correct equation is given in option c.
To know more about windmill, here
https://brainly.com/question/2031508
#SPJ4
The complete question is -
The blades of a windmill turn on an axis that is 35 feet above the ground. The blades are 10 feet long and complete two rotations every minute. Which of the following equations can be used to model h, the height in feet of the end of one blade, as a function of time, t, in seconds? Assume that the blade is pointing to the right, parallel to the ground at t = 0 seconds, and that the windmill turns counterclockwise at a constant rate.
a) h = −10sin(π15t)+35
b) h = −10sin(πt)+35
c) h = 10sin(π15t)+35
d) h = 10sin(πt)+35
Use integration to find the position function for the given velocity function and initial condition. (Rubric 10 marks) \[ v(t)=3 t^{3}+30 t^{2}+5 ; s(0)=3 \]
Answers
Answer:
\(\displaystyle s(t)=\frac{3}{4}t^3+10t^3+5t+3\)
Step-by-step explanation:
Integrate v(t) with respect to time
\(\displaystyle \int(3t^3+30t^2+5)\,dt\\\\=\frac{3}{4}t^4+10t^3+5t+C\)
Plug-in initial condition to get C
\(\displaystyle s(0)=\frac{3}{4}(0)^3+10(0)^3+5(0)+C\\\\3=C\)
Thus, the position function is \(\displaystyle s(t)=\frac{3}{4}t^3+10t^3+5t+3\) given the velocity function and initial condition.