What equation is equal to 2y= 2x + 2?
Answers
Answer:
y = x+1
Step-by-step explanation:
2y = 2x+2 ( divide both sides of the equation with 2)
y = x + 1
Related Questions
The entire seventh-grade class at Hobbes Junior High is having an ice cream party. The school conducted a survey about which kind of ice cream the students want for the party, with the choices of chocolate, vanilla, strawberry, and mint. The circle graph below shows the percentage of the class who voted for each flavor.
Approximately what percentage of the class voted for strawberry ice cream?
A. 30%
B. 60%
C. 20%
D. 10%

Answers
Answer:
Step-by-step explanation:
From the given circle graph, it can be observed that the "strawberry" wedge is approximately one-fourth (or 25%) of the entire circle.
Therefore, approximately 25% of the class voted for strawberry ice cream.
So, the closest option is A) 30%, but the more precise answer will be 25%.
precalculus problem need help

Answers
1. <C= 90 degree
AC = 13.25 unit
<B= 60 degree
2. <C= 90 degree
AC = 13.
<B= 60 degree
1. Using Sine law
sin C/4 = sin 30/2 = sin B/ AC
so, sin C/4 = 1/4
sin C = 1
C= 90 degree
and, <B= 180 - 30- 90= 60 degree
So, sin 30/2 = sin 60/ AC
1/4 AC = √3/2
AC = 2√3
2. Using Sine law
sin 30/ 7.65 = sin B / 15.3
1/15.3 = sin B/15.3
sin B= 1
B = 90 degree
and, <C= 180 - 90 - 30 = 60
So, 1/15.3 = sin 60/ C
C = 13.25
Learn more about Sine law here:
https://brainly.com/question/17289163
#SPJ1
90.10 rounded to the nearest whole number?
Answers
Answer:
it would be 90 because it has o be a 5 to 9 to round up but is a 1so you can round up
Step-by-step explanation:
Choose the most reasonable Celsius temperature for a snowy day.
17°C 26°C -6°C
Choose the most reasonable Celsius temperature for a snowy day.
O A. 26°C
OB. 17°C
C. -6°C
Answers
The most reasonable temperature for a snowy day is given as follows:
C. -6°C
How to obtain the most reasonable temperature?Considering that it snows, the temperature is either negative or very low positive, as snow only happens on temperatures close to freezing (like 2º C) or negative.
17ºC and 26ºC are far from cold enough to generate snow, hence the most reasonable temperature for a snowy day is given as follows:
C. -6°C
More can be learned about snow at https://brainly.com/question/18520972
#SPJ1
If the function y=sin(x) is transformed to y = sin(2x), how does the graph change?
It is stretched vertically.
It is compressed vertically.
It is stretched horizontally.
It is compressed horizontally..
Answers
Step-by-step explanation:
The transformation y = sin(2x) affects the graph of y = sin(x) by compressing it horizontally.
The function y = sin(2x) has a coefficient of 2 in front of the x variable. This means that for every x value in the original function, the transformed function will have half the x value.
To see the effect of this transformation, let's compare the graphs of y = sin(x) and y = sin(2x) by plotting some points:
For y = sin(x):
x = 0, y = 0
x = π/2, y = 1
x = π, y = 0
x = 3π/2, y = -1
x = 2π, y = 0
For y = sin(2x):
x = 0, y = 0
x = π/2, y = 0
x = π, y = 0
x = 3π/2, y = 0
x = 2π, y = 0
As you can see, the y-values of the transformed function remain the same as the original function at every x-value, while the x-values of the transformed function are compressed by a factor of 2. This means that the graph of y = sin(2x) appears narrower or more "squeezed" horizontally compared to y = sin(x).
Therefore, the correct statement is: It is compressed horizontally.
Dave is 4 years older than Colin. Ruth is three times as old as Dave. The total of their three ages is 56 Work out Ruth's age.
Answers
Answer:
Ruth is 36 years old
Step-by-step explanation:
let Colin's age be x , then
Dave's age is x + 4
Ruth's age is 3(x + 4) = 3x + 12
sum their ages and equate to 56
x + x + 4 + 3x + 12 = 56
5x + 16 = 56 ( subtract 16 from both sides )
5x = 40 ( divide both sides by 5 )
x = 8
Then
Ruth's age = 3x + 12 = 3(8) + 12 = 24 + 12 = 36
The age of Ruth is 36 years while Dave is 12 years old and Colin is 8 years old.
What is an equation?The equation is defined as mathematical statements that have a minimum of two terms containing variables or numbers that are equal.
Using variables to represent the ages of Colin and Dave:
C = Colin's age
D = Dave's age
From the given statement,
D = C + 4 (Dave is 4 years older than Colin)
We know that Ruth's age is three times Dave's age:
R = 3D (Ruth is three times as old as Dave)
Now, the sum of their ages is 56:
C + D + R = 56
Substituting the expressions for D and R in terms of C, we get:
C + (C + 4) + 3(C + 4) = 56
Simplifying and solving for C:
5C + 16 = 56
5C = 40
C = 8
So Colin is 8 years old. Using the expression for Dave's age in terms of C, we get:
D = C + 4 = 8 + 4 = 12
So, Dave is 12 years old.
Ruth's age in terms of D:
R = 3D = 3(12) = 36
Therefore, Ruth is 36 years old.
Learn more about the equations here:
brainly.com/question/10413253
#SPJ2
is -4 an even or odd numnber?
Answers
Answer:
An even number
Step-by-step explanation:
Integers which are multiples of 2, are even numbers.
Integers which aren't multiples of 2, are odd numbers.
As integers can be positive and negative both, odd and even numbers also can be positive and negative.
Assume that a sample is used to estimate a population proportion p. Find the margin of error E that corresponds to
the given statistics and confidence level. Round the margin of error to four decimal places
98% confidence; the sample size is 800. of which 40% are successes
Answers
The error E = ± 4.04 %
Sample data = ( p ).
success p = success percentage = 40 %
confidence interval CI = 98%
sample size n = 800
margin of error E:
The margin of error "E" for estimation of population proportion ( p ) is given by:
E = z - critical √(p(1-p)/n)
P ( Z < Z-critical ) = a/
a = 1 - CI
P ( Z < Z-critical ) = (1 - 0.98) / 2
P ( Z < Z-critical ) = 0.01
Z-critical = 2.33
The error E = ± 4.04 %
Thus, the correct answer is E=± 4.04 %
Learn more about margin of error:
brainly.com/question/13031441
#SPJ1
During the first couple weeks of a new flu outbreak, the disease spreads according to the equation I(t) = 3900e^0.0514, where I(t) is the number of infected people t days after the outbreak was first identified. Find the rate at which the infected population is growing after 8 days and select the appropriate units.
Answers
The rate at which the infected population is growing after 8 days of the outbreak is approximately 1096.57 people per day, as determined by the derivative of the given function with respect to time.
To find the rate at which the infected population is growing after 8 days, we need to take the derivative of the given function I(t) with respect to t:
\(dI/dt = 3900(0.0514)e^(0.0514t)\)
At t=8, the rate at which the infected population is growing is:
\(dI/dt = 3900(0.0514)e^(0.0514*8) = 1096.57\)
Therefore, the rate at which the infected population is growing after 8 days is approximately 1096.57 people per day.
It is important to note that this rate of growth is an instantaneous rate at t=8, and it will likely change as time passes and the outbreak progresses. Furthermore, the rate of growth of the infected population depends on various factors such as the transmission rate of the virus, the effectiveness of preventive measures, and the availability of healthcare resources.
In conclusion, the rate at which the infected population is growing after 8 days of the outbreak is approximately 1096.57 people per day, as determined by the derivative of the given function with respect to time. This result provides insight into the early stages of a flu outbreak, but further analysis is required to understand the longer-term dynamics of the outbreak and the factors that affect the spread of the disease.
To know more about instantaneous rate refer here:
https://brainly.com/question/18235056
#SPJ11
\( \rm\int_0^{\pi/2} \ln(1+4\sin^4 x)\text{ d}x \\ \)
Answers
The integration of the function; ∫In( 1 + 4sin⁴x) dx between the boundaries π/2 and 0 is; 0.0966
How to integrate trigonometric functions?
We want to carry out the integration of the function;
∫In( 1 + 4sin⁴x) dx
We want to integrate this between the boundaries π/2 and 0.
Thus;
∫In( 1 + 4sin⁴x) dx = [In (sin (4x)) - 8 sin(2x) + 44x)]/32
Now, between the given boundaries, we have;
[In (sin (4π/2)) - 8 sin(2*π/2) + 44*π/2)]/32 - [In (sin (4*0)) - 8 sin(2*0) + 44*0)]/32
= [In (sin (2π)) - 8 sin(π/) + 22π)]/32
= [In(22)]/32 = 0.0966
Read more about Integration at; https://brainly.com/question/28156093
#SPJ1
A normally distributed data set has a mean of 0 and a standard deviation of 0.5. Which is closest to the percent of values between –1 and 1?
34%
50%
68%
95%
Answers
As a result, 68% of the data falls into the range of values between -1 and 1, which is one standard deviation from the mean. The closest estimate of the solution is 68%.
What is equation?A mathematical equation is a formula that connects two claims and uses the equals symbol (=) to denote equivalence. An equation in algebra is a mathematical statement that establishes the equivalence of two mathematical expressions. For instance, in the equation 3x + 5 = 14, the equal sign places a space between the variables 3x + 5 and 14. The relationship between the two sentences that are written on each side of a letter may be understood using a mathematical formula. The symbol and the single variable are frequently the same. as in, 2x - 4 equals 2, for instance.
For a normally distributed data set with a mean of 0 and a standard deviation of 0.5, the proportion of values between -1 and 1 is most closely related to 68%.
Approximately 68% of the data in a normal distribution lies within one standard deviation of the mean, which explains why. One standard deviation below the mean is -0.5, and one standard deviation above the mean is 0.5 since the mean is 0 and the standard deviation is 0.5. As a result, 68% of the data falls into the range of values between -1 and 1, which is one standard deviation from the mean. The closest estimate of the solution is 68%.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
A student's height is measured as 66 in. to the nearest inch. What are the
student's minimum and maximum possible heights?
Answers
Dad is twice as old as Junior. Gramps is twice as old as Dad. The sum of the three ages is 140. How old is Gramps?
Answers
Answer:
80
Step-by-step explanation:
We can start of with Junior's age. Then if dad is twice as old as Junior, then we add 2 parts and get 3 parts. Then Gramps is twice as old as Dad so we add 4 parts and get 7 parts. Now we divided 140 by 7. We get 20. This is Junior's age. By looking at that, we know Dad is 40, and Gramps is 80.
Gramps is 80 years old.
Hi! I'm happy to help!
We can say that Junior is x years old. This would mean that Dad is 2x years old, and Gramps is 4x years old. All together, their age is 7x. We can write an equation to solve.
7x=140
Divide both sides by 7 to find out x.
x=20
This means that Junior is 20 years old. Dad is double that, so he is 40 years old. And Gramps is double that so he is 80 years old.
To check our answer we can add all of them together.
20+40+80
140
This means that Gramps is 80 years old.
I hope this was helpful, keep learning! :D
Toby rode his bike 7 miles each day for
26 weeks. Wendy rode 200 miles each month for 6 months.
Who rode their bike farther? How much farther? Explain.
Answers
Answer:
Toby rode his bike further. He rode 74 miles further than Wendy.
Step-by-step explanation:
7 miles per day for 26 weeks is, 7 times 7 times 26, which is a total of 1274 miles. 200 miles each month for 6 months is 6 times 200, which equals 1,200 miles. Toby rode more miles.
Which of the equations below could be the equation of this parabola?
OA y--¹x²
OB. x--²
C. x-²
D. y - x²
10
(0,0)
Vertex
10
Answers
An equation that could be the equation of this parabola include the following: C. x = 1/12(y²).
How to determine the equation of a parabola?In Mathematics, the standard equation of the directrix lines for any parabola that opens to the right is represented by this mathematical expression:
x = a(y - k)² + h.
Where:
h and k represent the vertex.a represent the leading coefficient.By critically observing the graph which models the equation of this parabola, we can logically deduce that the vertex is at point (0, 0) and as such, we have the following:
h = 0
k = 0
a = positive.
x = a(y - k)² + h.
x = a(y - 0)² + 0.
x = ay²
Therefore, a possible equation is x = 1/12(y²).
Read more on parabola here: https://brainly.com/question/7700497
#SPJ1

A recent food drive distributed 6,298 pounds of stoneground cornmeal to 1,007 people. Approximately how many pounds did each person receive? Round to the hundredths.
Answers
Answer: 6.25
Step-by-step explanation: Here, you want to find how much of 6,298 pounds of food each person got. You can do this by dividing. 6,298/1,007 should get you the answer because it shows how the 6,298 pounds were distributed amongst the 1,007 people.
What is an example of "A one-to-one function of P onto Q is an isomorphism of P and Q "?

Answers
An example of a one-to-one function that is an isomorphism between sets P and Q is the function f: P -> Q defined as f(x) = 2x, where P and Q are the sets of integers.
How to Identify a One-to-One Function?An example of a one-to-one function that is an isomorphism between sets P and Q is the function f: P -> Q defined as f(x) = 2x, where P and Q are the sets of integers.
This function is one-to-one because for every element x in P, there is a unique element 2x in Q. It is onto because every element y in Q has a preimage x in P such that f(x) = y (e.g., y/2 = x).
Furthermore, this function preserves the group structure between P and Q, as it satisfies the properties of an isomorphism. In this case, the group structure is addition, and the function f preserves addition: f(x + y) = 2(x + y) = 2x + 2y = f(x) + f(y) for all x, y in P.
Therefore, the function f: P -> Q defined as f(x) = 2x is an example of a one-to-one function that is an isomorphism between sets P and Q.
Read more about One-to-One Function at: https://brainly.com/question/30563810
#SPJ1
which ordered pair (x,y) is the solution to the given system of linear equations 3x + 3y = -3-2x + y = 2
Answers
Joel, this is the solution:
3x + 3y = -3
-2x + y = 2
____________
Step 1: Isolating x on the 1st equation:
3x + 3y = -3
3x = - 3 - 3y
Dividing by 3 at both sides:
3x/3 = -3/3 - 3y/3
x = -1 - y
Step 2: Substituting x on the 2nd equation and solving for y:
-2x + y = 2
-2(-1 - y) + y = 2
2 + 2y + y = 2
3y = 2 - 2
3y = 0
y = 0
Step 3: Substituting y on the 1st equation and solving for x:
3x + 3y = -3
3x + 3 * 0 = -3
3x + 0 = -3
Dividing by 3 at both sides:
3x/3 = -3/3
x = -1
Now, Joel, we can select the correct choice:
A. (-1, 0)
Find R. Round to the nearest tenth.

Answers
Answer:
letter R rounded off to the nearest tenth is 40
15 is the answer because this is the nearest
Find the parametric equation of
X=4sin(5t)
Y=-48sin^2(5t)+8sin(5t)-3
Answers
The parametric equations for the curve are X = 4 sin(5t), Y = -48 sin²(5t) + 8 sin(5t) + 45
Describe Parametric Equation?A parametric equation is a set of equations that express the coordinates of a point as functions of one or more parameters. These equations define a curve or a surface in a space and are commonly used in mathematics, physics, engineering, and computer graphics to model and analyze various phenomena.
Parametric equations can be useful in many applications, such as modeling the motion of particles, designing curves and surfaces, and creating computer animations. They also allow for the visualization of complex shapes and curves that may be difficult to describe using traditional equations.
To find the parametric equation of the given curve, we need to express the coordinates x and y in terms of a parameter t. We can use the trigonometric identities to simplify the given equations and get:
X = 4 sin(5t)
Y = -48 sin²(5t) + 8 sin(5t) - 3
Let's start with Y. We can use the identity sin²(θ) + cos²(θ) = 1 to rewrite -48 sin²(5t) as -48 (1 - cos²(5t)) = -48 cos²(5t) + 48. Substituting this into the equation for Y, we get:
Y = -48 cos²(5t) + 8 sin(5t) - 3
Now, we can use another trigonometric identity, sin²(θ) + cos²(θ) = 1, to rewrite cos²(5t) as 1 - sin²(5t). Substituting this into the equation for Y, we get:
Y = -48 (1 - sin²(5t)) + 8 sin(5t) - 3
Y = -48 sin²(5t) + 8 sin(5t) + 45
So, the parametric equations for the curve are:
X = 4 sin(5t)
Y = -48 sin²(5t) + 8 sin(5t) + 45
This is the final answer.
To know more about curve visit:
https://brainly.com/question/28537985
#SPJ1
What is the slope of the line shown below?
10
(-5, -1)
10
-10
y
10
5
(5, 11)
10
15
O
A.
B.
O C.
O D.
96

Answers
The slope of the line is C) \(\frac{6}{5}\).
What is slope?
Calculated using the slope of a line formula, the ratio of "vertical change" to "horizontal change" between two different locations on a line is determined. The difference between the line's y and x coordinate changes is known as the slope of the line. Any two distinct places along the line can be used to determine the slope of any line.
Here the given point is \((x_1,y_1)=(-5,-1)\) and \((x_2,y_2)=(5,11)\)
Now using slope formula then,
=> Slope m = \(\frac{y_2-y_1}{x_2-x_1}\)
=> Slope m = \(\frac{11-(-1)}{5-(-5)}\)
=> slope m = \(\frac{11+1}{5+5}\)
=> slope m = \(\frac{12}{10}\)
=> slope m = \(\frac{6}{5}\)
Hence the slope of the line is C) \(\frac{6}{5}\).
To learn more about slope refer the below link
https://brainly.com/question/16949303
#SPJ1
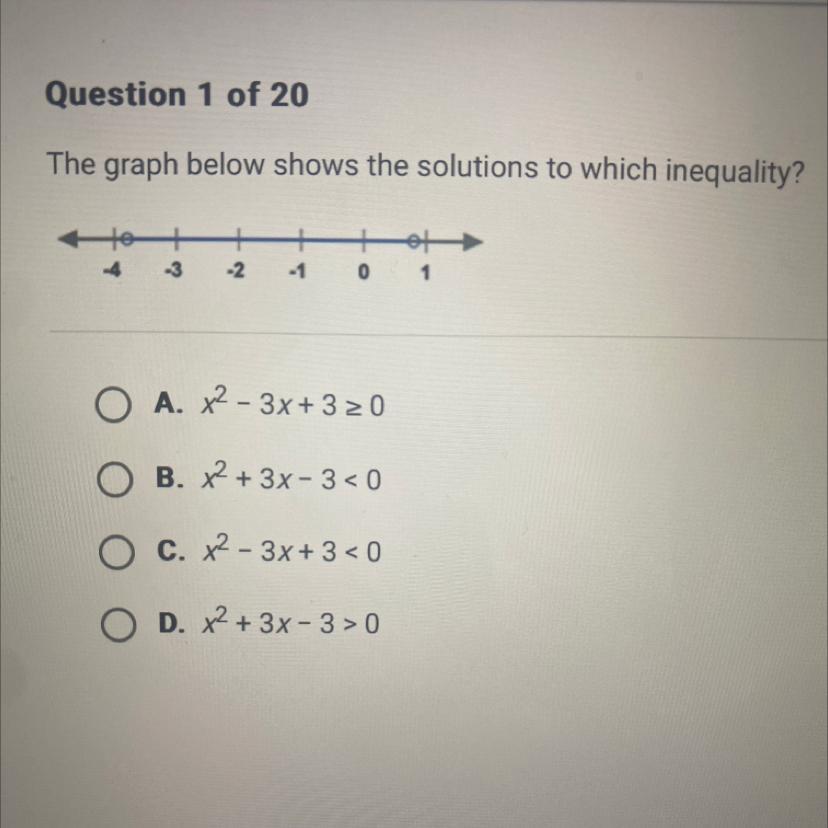
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
Beginning with the graph of f(x) = x2, what transformations are needed to form g of x equals one third times the quantity x plus 3 end quantity squared minus 3 question mark?
Answers
To transform f(x) into g(x) we need to use addition, subtraction and multiplication.
Given f(x)=\(x^{2}\) and g(x)=\(x/3+3(x^{2} -3)\)
We need to transform function f(x)into g(x).
A function refers to a relation which expresses relationship between two variables. It contains one value for each value of x. If there are more than one value for one value of x then it is not said to be a function.
f(x)=\(x^{2}\), g(x)=\(x/3+3(x^{2} -3)\)
To transform f(x) into g(x) we need to follow the following steps:
First subtract 3 from f(x).Then multiply the expression received from above step by 3.Next step is to add x/3 to the expression received from the above step.Now we will get the g(x)=\(x/3+3(x^{2} -3)\).Hence we have to use addition, subtraction and multiplication for transformation.
Learn more about function at https://brainly.com/question/10439235
#SPJ10
The graph of g(x) is wider than f(x) and is shifted to the left 4 units and down 3 units.
Step-by-step explanation:
fill in the missing values.
help!!

Answers
it is 4 3 2 1 5 6 4 3 3. 6 5 3 3 5 5 3 4 5 4
Would appreciate some math help!

Answers
Answer:
\( - \sqrt{ \frac{2}{3} } \)
what's the 9th term of the fibonacci sequence
Answers
Answer:
21
Step-by-step explanation:
i hope this helps :)
Answer:
.where is the explanation?
The regular price of a chair is $175.90. Find the sale price of the chair
If the regular price is reduced by 10 %, and the new price is then reduced by 15%
Answers
Answer:
134.56
Step-by-step explanation:
I believe the sale price for the chair would be 134.56 hope this helps
Answer:
$ 134.56
Step-by-step explanation:
Regular price = $175 .90
Reduction = 10% of 175.90
= 17.59
Price after reduction = 175.90 - 17.59 = $ 158.31
Second reduction = 15% of 158.31
= 0.15 * 158.31
= 23.7465
= $ 23.75
New price = 158.31 - 23.75
= $ 134.56
Please help me w this hehehehehh

Answers
Answer:
-25x-45y, because if we have got + and -, so we will write minus.
One-sixth of the sum of x and 3 minus the product of 9 and p
Answers
Hey there! I'm happy to help!
We have the sum of x and 3.
x+3
One-sixth of that.
1/6(x+3)
Minus the product of 9 and p
1/6(x+3)-9p
Have a wonderful day! :D
Select the best answer for the question.
4. Multiply 3/4 * 16/9
A. 4/3
B.3/4
C. 64/27
D. 27/64
Answers
Answer:
A. 4/3
3/4 *16/9 =
(3*16)/ (4*9) =
48/36 =
12*4/12*3 =
4/3