Use the trapezoidal approximation to estimate he distance the turtle traveled from 0 to 10 seconds.

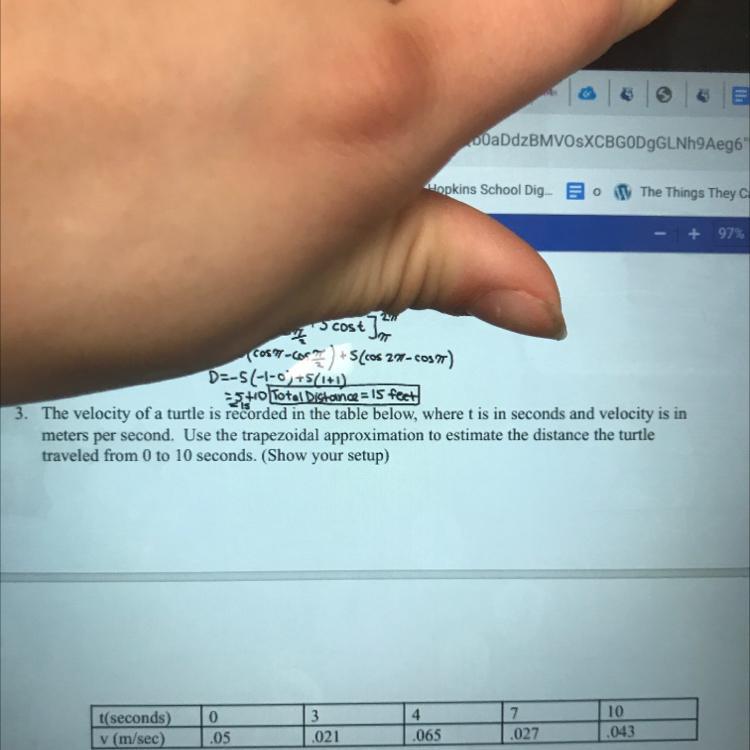
Answer:

Step-by-step explanation:

First, you could factor 2 out of the whole thing.  The result would be 2(x^2-4x-45). Now we find the factors of 45 which are 1, 45, 5, 9, 15, 3. We have to find the pair that adds up to 4, and multiply to get 45. After some guess and check, we can find that 5 and 9 are those numbers. Now we have to get the right signs. Since the result is a negative number for -8k, and -90, the number that is a negative must be less than the other negative. -9<-5, so the answer would be 2(x-9)(x+5)

At a price of $3, the total revenue will be the greatest, and the company will sell 3 units at that price.

To find the total revenue at each price, we can multiply the price by the corresponding quantity.

Price        Quantity          Total Revenue

$6                0                      $0

$5                 1                       $5

$4                 2                       $8

$3                 3                        $9

$2                 4                         $8

$1                  5                          $5

To find the price at which total revenue is the greatest, we look for the highest value in the Total Revenue column.

In this case, the highest total revenue is $9, which occurs when the price is $3.

At a price of $3, the company will sell 3 units (as indicated in the Quantity column).

To learn more on Revenue click:

https://brainly.com/question/14952769

#SPJ1

Answer:

Step-by-step explanation:

4/5 - 9/12 = 48/60 - 45/60 = 3/60 = 1/20

Answer:

-2

Step-by-step explanation:

Answer:

Step-by-step explanation:

Select a pair that has two angles and the included side marked

Correct choice is B

Given

Rectangle area is the product of its sides.

Side MN is 5 as per difference in x- coordinates.

The other side has length of 20/5 = 4 units.

Side KL is side MN elevated 4 units up.

So the point L has coordinates (0,4) and K has coordinates of (5, 4)

Correct choice is B

hope this helps

by

aman10we

The value of x after solving this equation is 2

Polynomial is made up of two terms, namely Poly (meaning “many”) and Nominal (meaning “terms.”). A polynomial is an expression composed of variables, constants, and exponents, combined using mathematical operations such as addition, subtraction, multiplication, and division (No division operation by a variable). Based on the number of terms present in the expression, it is classified as monomial, binomial, and trinomial. For example P(x) = x2-5x+11

Given here, the equation as : (4x - 5)^4 = 81.​

(4x - 5)^4 = 3⁴.​

4x - 5    = 3

      x     = 2

Hence, the value of x is equal to 2

Learn more about polynomials here:

https://brainly.com/question/11536910

#SPJ2

The area is 108yd2(square yards).

In the given triangle a base

24yd and the corresponding height of 6 yds are given, so to calculate the area we can use:

A=12×b×h

If we substitute the given numbers we get:

A=\(\frac{1}{2}\)×24×18

=12×9

=108

The units of base and height are the same (yards), so the calculated area is in yd2

The area is the quantity that expresses the extent of a region on the plane or on a curved surface. the world of a plane region or plane area refers to the area of a shape or planar lamina, while area refers to the area of an open surface or the boundary of a three-dimensional object. The area is often understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the quantity of paint necessary to cover the surface with a single coat. it's the two-dimensional analog of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept).

To  learn more about the area from the given link:

brainly.com/question/27683633

#SPJ9

Alexander is utilizing a scale of 1 inch : 300 feet for his map.

The Alexander's triangle has a height of 4 inches in inches.

When comparing the initial dimensions as used by alexander, the scale of the map may be determined.

The scale is 1 inch: 300 feet since he used 10 inches to symbolize 3000 feet, this is gotten by diving both sides by 10

Using the scale factor 1 inch: 300 feet, the height of 1200 feet would be.

300 feet per inch, then ? inch is 1200 feet

? * 300 = 1200 * 1

? = 1200 / 300

? = 4 inches

Read more on scale factor here:

brainly.com/question/8159270

#SPJ1

Answer:

Brand A  Costs 37.38 per ounce and Brand B cost 31.19 per ounce hope this helped ^-^

Answer: 2xy • (4x - 5y)

Step-by-step explanation:

STEP 1:

Equation at the end of step 1

 ((8 • (x2)) • y) -  (2•5xy2)

STEP 2:

Equation at the end of step 2:

 (23x2 • y) -  (2•5xy2)

STEP 3:

STEP 4:

Pulling out like terms

4.1     Pull out like factors :

  8x2y - 10xy2  =   2xy • (4x - 5y)

Final result :

 2xy • (4x - 5y)

there you go i think

Answer:

-4.5,  -0.5, 0.3, 0.7, 2.3

Step-by-step explanation:

The 3 parts of a parabola are the vertex ,the focus and the directrix . Other parts includes  the axis (parallel to the y axis),the focal length , the semi-latus rectum etc.

Parabola's vertex

In addition to serving as the parabola's opening point, the vertex also serves as a location indicator. Typically, the point V of the vertex is used to represent it.

Directrix

The directrix of the parabola is a straight line that, together with the focus (a point), is used in one of the most common definition of parabolas.

Focus

The focus of a parabola is a fixed point on the interior of a parabola used in the formal definition of the curve.

To learn more about parabolas

https://brainly.com/question/21685473

#SPJ4

Answer:

70 ft

Step-by-step explanation:

To find the height of the building, we can use the trigonometric relationship between the angle of elevation, the distance from the object, and the height of the object.

In this case, we have a right triangle formed by the observer, the top of the building, and the base of the building. Therefore, we can use the tangent trigonometric ratio, since the height of the building is the opposite the angle of elevation, and the distance between the observer and the building is the side adjacent the angle.

\(\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=\dfrac{O}{A}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}\)

Let "x" be the height of the building.

Let "d" be the initial distance from the observer to the building.

The angle of elevation changes from 15° to 30° as the observer advances 140 feet toward the building.

(See the attachment for a visual representation).

Based on this information, we can set up the following equations:

\(\tan 15^{\circ}=\dfrac{x}{d}\)

\(\tan 30^{\circ}=\dfrac{x}{d-140}\)

Rearrange both equations to isolate d:

\(d=\dfrac{x}{\tan 15^{\circ}}\)

\(d=\dfrac{x}{\tan 30^{\circ}}+140\)

Solve this system of equations by the method of substitution.

\(\dfrac{x}{\tan 15^{\circ}}=\dfrac{x}{\tan 30^{\circ}}+140\)

\(\dfrac{x}{\tan 15^{\circ}}-\dfrac{x}{\tan 30^{\circ}}=140\)

\(\dfrac{x\tan 30^{\circ}-x \tan 15^{\circ}}{\tan 30^{\circ}\tan 15^{\circ}}=140\)

\(\dfrac{x(\tan 30^{\circ}- \tan 15^{\circ})}{\tan 30^{\circ}\tan 15^{\circ}}=140\)

\(x=\dfrac{140\tan 30^{\circ}\tan 15^{\circ}}{\tan 30^{\circ}- \tan 15^{\circ}}\)

\(x=\dfrac{140\cdot \frac{\sqrt{3}}{3}(2-\sqrt{3})}{\frac{\sqrt{3}}{3}- (2-\sqrt{3})}\)

\(x=\dfrac{\dfrac{140(2\sqrt{3}-3)}{3}}{\dfrac{4\sqrt{3}-6}{3}}\)

\(x=\dfrac{140(2\sqrt{3}-3)}{2(2\sqrt{3}-3)}\)

\(x=\dfrac{140}{2}\)

\(x=70\)

Therefore, the height of the building is exactly 70 feet.

The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.

To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.

Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.

To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:

P(x) = x(24 - x)

This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.

The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.

To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.

Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.

So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.

Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.

To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]

For more such question on function. visit :

https://brainly.com/question/11624077

#SPJ8

Answer: D

Step-by-step explanation: 3 goes in to 57, 19 times and 19 goes into 57, 3 times. No other components other than 1 and 59

Answer:

D

Step-by-step explanation:

T4L 2021

Yes, 7/56 and 6/48 are proportional because 7×48 = 56×6. Therefore, the correct answer is option B.

Given that, a truck needs 7 gallons of fuel to travel 56 miles.

The truck travel 48 miles with 6 gallons of fuel.

Here, the proportion is

7:56::6:48

We know that, the proportion is product of extremes = product of means

7×48 = 56×6

336 = 336

Therefore, the correct answer is option B.

To learn more about the proportional relationship visit:

brainly.com/question/12917806.

#SPJ1

We have to calculate how much is the annual premium per week

If the employer deducts the 50% from her paycheck, then

243.42 (0.5) = $121.71

(a) There are 2 sequences of length 1 that fit the bill: 0 and 1. So if \(b_n\) is the number of permissible sequences, then \(b_1=2\).

To the sequence 0, we can attach either 0 or 1 at the end, while the sequence 1 must be followed by 0. Then the permissible sequences of length 2 are 00, 01, and 10, so \(b_2=3\).

Now consider a sequence of length n + 1, of which there are \(b_{n+1}\).

• If the last digit is 0, then we got this sequence by simply joining 0 to one of \(b_n\) sequences. In other words, there are \(b_n\) permissible sequences of length n + 1 that end in 0.

• If the last digit is 1, then the previous digit must have been 0. Put another way, we join 01 to a permissible sequence of length n - 1 (there are \(b_{n-1}\) of them). So there are \(b_{n-1}\) permissible sequences of length n + 1 that end in 1.

These cases are mutually exclusive, so the number of (n + 1)-length permissible sequences is given by

\(\begin{cases}b_1 = 2 \\ b_2 = 3 \\ b_{n+1} = b_n + b_{n-2} & \text{for }n\ge2\end{cases}\)

(b) The reasoning for a permissible ternary sequence is similar. Let \(t_n\) be the number of sequences of length n not containing 11.

We first note that \(t_1 = 3\), since we can have 0, 1, or 2; and \(t_2 =  8\), since we can have 00, 01, 02, 10, 12, 20, 21, or 22.

Consider a sequence of length n + 1 (\(t_{n+1}\) of these).

• If the last digit is 0, then we joined 0 to a permissible sequence of length n. So there are \(t_n\) permissible sequences of length n + 1 ending in 0.

• If the last digit is 1, then the last two digits must be either 01 or 21. Since there are 2 choices for the n-th digit, there are \(2t_{n-1}\) permissible sequences of length n + 1 ending in 1.

• If the last digit is 2, then we essentially have the same situation as if the sequence ended in 0, so there are \(t_n\) sequences of length n + 1 ending in 2.

Then the recurrence for ternary permissible sequences is

\(\begin{cases}t_1 = 3 \\ t_2 = 8 \\ t_{n+1} = 2t_n + 2t_{n-1} & \text{for }n\ge2\end{cases}\)

A uniform random variable's density function is f(y) = 1 for y 1 and 0 otherwise. F(y) = 0 for y 0, F(y) = y for 0 y 1, and F(y) = 1 for y > 1 define the distribution function.

A uniform random variable's density function is f(y) = 1 for y 1 and 0 otherwise. Accordingly, the likelihood of any specific outcome of y is the same, and the likelihood of any range of outcomes is equal to the length of the range. F(y) = 0 for y 0, F(y) = y for 0 y 1, and F(y) = 1 for y > 1 define the distribution function. Accordingly, the length of the range multiplied by the likelihood of any specific occurrence yields the cumulative probability of any range of outcomes. Since the likelihood of any specific result in that range is 1 and the range's length is 0.5, for instance, the cumulative probability of 0 y 0.5 is 0.5. Since the likelihood of any given result within that range is still 1, but the range's length is 0.5, the cumulative probability of 0.5 y 1 is 0.75. The chance of any range of outcomes for y1 and y2 if they are independent random variables both having the uniform(0,1) distribution is just the sum of their respective cumulative probabilities.

Learn more about variable here

brainly.com/question/29583350

#SPJ4

Answer:

Axis of symmetry =1

vertex =(1,2)

y intercept =0

min/max= -6,2

domain= 0,1,2

range =y≥1,2

Answer:

-3

Step-by-step explanation:

i sarched it up

The volume of cone is 175 m³

Firstly,

Volume of Pyramid.

The volume (V) of a pyramid is  

V = ⅓Ah

Data:

V = 175m³

Calculation:

175 = ⅓× A× h

Ah = 175*3

Ah = 525m³

Secondly,

The volume (V) of a cone is

V = ⅓Ah

Data:

Ah = 525 m³

Calculation:

V = ⅓ A× h

V = 175 m³

Know more about volumes,

https://brainly.com/question/17101095

#SPJ1

The correct statement is: On a coordinate plane, an absolute value graph has a vertex at (0, 1).

The function p(x) = |x - 1| represents an absolute value function. The vertex of an absolute value function in the form f(x) = |x - h| + k is given by the point (h, k). In this case, the function p(x) = |x - 1| has a vertex at (1, 0).

Therefore, none of the provided options accurately represents the vertex of the function p(x) = |x - 1|. The correct vertex for this function is (1, 0), which means the vertex is at x = 1 and y = 0 on the coordinate plane. It is important to note that the vertex is located at (h, k) where h represents the x-coordinate and k represents the y-coordinate.

For more such questions on graph

https://brainly.com/question/19040584

#SPJ8

The probability of being a male and derive from a group of employees were asked whether they drive or walk to work is equal to 0.27.

From the table representing the probabilities of a group of employees.

Employees divided into two groups,

One is male .

Second is female.

While going for work there are two ways .

Derive to walk.

Walk to work.

Different probabilities are as follow,

Male and derive 0.27

Male and walk = 0.27

Female and derive = 0.23

Female and walk = 0.23

The required probability of being a male and derive

= 0.27.

Therefore, the probability of derive and male is equal to 0.27.

learn more about probability here

brainly.com/question/30034780

#SPJ1

Answer:

33 , 39

Step-by-step explanation:

given

9 , 15 , 21 , 27

there is a common difference between consecutive terms, that is

15 - 9 = 21 - 15 = 27 - 21 = 6

to obtain terms in the sequence add 6 to the preceding term

27 + 6 = 33

33 + 6 = 39

the next two terms are 33 and 39

The standard form of the equation for the circle is\((x - 4)^2 + (y - 3)^2 = 2.\)

To find the standard form of the equation for the circle, we need to determine the center and radius of the circle using the given information.

The center of the circle can be found by taking the average of the x-coordinates and the y-coordinates of points A and B.

Center:

x-coordinate = (3 + 5) / 2 = 4

y-coordinate = (2 + 4) / 2 = 3

The center of the circle is (4, 3).

Next, we need to find the radius of the circle.

The radius is the distance between the center of the circle and any point on its circumference.

In this case, we can use the distance formula between the center (4, 3) and point B (5, 4).

Radius:

\(r = \sqrt{((5 - 4)^2 + (4 - 3)^2)}\)

= \(\sqrt{(1 + 1)}\)

\(=\sqrt{(2)}\)

The radius of the circle is \(\sqrt{(2).}\)

Now we can write the standard form of the equation for the circle, which is:

\((x - h)^2 + (y - k)^2 = r^2\)

Plugging in the values we found:

\((x - 4)^2 + (y - 3)^2 = 2\)

For similar question on standard form.

https://brainly.com/question/19169731  

#SPJ8

The function m(x) = 2tan(3x+4) is obtained by applying a sequence of transformations to the parent tangent function.

To determine the sequence of transformations, let's break down the given function:

1. Inside the tangent function, we have the expression (3x+4). This represents a horizontal compression and translation.

2. The coefficient 3 in front of x causes the function to compress horizontally by a factor of 1/3. This means that the period of the function is shortened to one-third of the parent tangent function's period.

3. The constant term 4 inside the parentheses shifts the function horizontally to the left by 4 units. So, the graph of the function is shifted to the left by 4 units.

4. Outside the tangent function, we have the coefficient 2. This represents a vertical stretch.

5. The coefficient 2 multiplies the output of the tangent function by 2, resulting in a vertical stretch. This means that the graph of the function is stretched vertically by a factor of 2.

In summary, the sequence of transformations applied to the parent tangent function to create the function m(x) = 2tan(3x+4) is a horizontal compression by a factor of 1/3, a horizontal shift to the left by 4 units, and a vertical stretch by a factor of 2.

Example:
Let's consider a point on the parent tangent function, such as (0,0), which lies on the x-axis.

After applying the transformations, the corresponding point on the function m(x) = 2tan(3x+4) would be:
(0,0) -> (0,0) (since there is no vertical shift in this case)

This example helps illustrate the effect of the transformations on the graph of the function.

For more question on expression

https://brainly.com/question/1859113

#SPJ8