Use an element argument to prove the statement. (Assume that all sets are subsets of a universal set U.)
Statement: For all sets A, B, and C, (A − B) ∩ (C − B) = (A ∩ C) − B.
Answers
Answer and Step-by-step explanation:
Solution:
Given:
A, B and C are sets.
We have to prove that:
(A − B) ∩ (C − B) = (A ∩ C) − B.
Use an element x,
Let x Є (A – B), by the definition of difference:
X Є A and x ∉ B.
And
X Є A ∩ C and x ∉ B
X Є (A ∩ C) – B
Now let x Є C – B
By the definition of difference:
X Є C and x ∉ B
By definition of intersection: x Є C and x Є( A ∩ C)
By definition of difference, using that x Є(A ∩ C) And x ∉ B:
X Є ( A ∩ C) – B
We know that: x Є (A – B) ∩ ( C – B)
Is equivalent to x Є A – B and x Є C – B
So, ( x Є A and x ∉ B)
And (x Є C and x ∉ B)
From this we know that x Є (A ∩ C) – B.
Related Questions
1 1/2 = 2x
what is the answer?
Answers
Answer:
3/4
Step-by-step explanation:
Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] f(x) = 4 cos(x), a = 7π
Answers
Answer:
The Taylor series of f(x) around the point a, can be written as:
\(f(x) = f(a) + \frac{df}{dx}(a)*(x -a) + (1/2!)\frac{d^2f}{dx^2}(a)*(x - a)^2 + .....\)
Here we have:
f(x) = 4*cos(x)
a = 7*pi
then, let's calculate each part:
f(a) = 4*cos(7*pi) = -4
df/dx = -4*sin(x)
(df/dx)(a) = -4*sin(7*pi) = 0
(d^2f)/(dx^2) = -4*cos(x)
(d^2f)/(dx^2)(a) = -4*cos(7*pi) = 4
Here we already can see two things:
the odd derivatives will have a sin(x) function that is zero when evaluated in x = 7*pi, and we also can see that the sign will alternate between consecutive terms.
so we only will work with the even powers of the series:
f(x) = -4 + (1/2!)*4*(x - 7*pi)^2 - (1/4!)*4*(x - 7*pi)^4 + ....
So we can write it as:
f(x) = ∑fₙ
Such that the n-th term can written as:
\(fn = (-1)^{2n + 1}*4*(x - 7*pi)^{2n}\)
In this exercise we must calculate the Taylor series for the given function in this way;
\(f_n= (-1)^{2n+1}(4)(x-7\pi)^{2n}\)
The Taylor series of f(x) around the point a, can be written as:
\(f(x) = f(a) + f'(a)(x-a)+\frac{1}{2!} f''(a)(x-a)^2+....\)
Here we have:
\(f(x) = 4cos(x)\\a = 7\pi\)
Then, let's calculate each part:
\(f(a) = 4cos(7\pi) = -4\\df/dx = -4sin(x)\\(df/dx)(a) = -4sin(7\pi) = 0\\(d^2f)/(dx^2) = -4cos(x)\\(d^2f)/(dx^2)(a) = -4cos(7\pi) = 4\)
Here we already can see two things:
1) The odd derivatives will have a sin(x) function that is zero when evaluated in \(x=7\pi\).
2) We also can see that the sign will alternate between consecutive terms.
So we only will work with the even powers of the series:
\(f(x) = -4 + (1/2!)*4*(x - 7\pi)^2 - (1/4!)*4*(x - 7\pi)^4 + ....\)
So we can write it as:
\(f(x)=\sum f_n\)
Such that the n-th term can written as:
\(f_n= (-1)^{2n+1}(4)(x-7\pi)^{2n}\)
See more abour Taylor series at: brainly.com/question/6953942
six fifths, eight ninths, 0.5, forty percent?
Answers
Answer:
I'm assuming this is a greatest to least, but in case it was not, I put least to greatest, too.
Step-by-step explanation:
Greatest to least:
6/5, 8/9, 0.5, 40%
Least to greatest:
40%, 0.5, 8/9, 6/5
Hope this helps!
determine the quotient of 1 1/3÷ 3/5

Answers
Answer:
c
Step-by-step explanation:
4/3
3/5
keep change fli[
20/9=2 2/9
Geometry Section 58C/School Year/
For the three-part question that follows, provide your answer to each part in the given workspace. Identify each part with a coordinating response. Be sure to clearly label each part of your response as Part A
Part B, and Part C
Part A: How many triangles can be formed if the measurements of a triangle are a 27,6-15, A-557
Part B: Explain how to determine the answer to Part A
Part C: Find all possible solutions for this triangle.
BiFont Family -AA-A
11
P Type here to search
ii
LE
8
DELL
I
PREVIOUS
19 of 23
NEXT
nomad
SAVE & EXT
3:00 PM
3/14/2023

Answers
1. Triangle inequality theorem.
3. The missing lengths and angles are:
<B = 27.07, <C = 98 and c = 32.64.
1. According to triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
2. To determine the number of triangles that can be formed, we can use the given measurements and check if the triangle inequality theorem is satisfied.
3. We have,
a = 27, b = 15, and A = 55°,
Using the Law of Sines,
sin A/ a = sin B/ b
sin 55 /27 = sin B / 15
0.81915204428 / 27 = sin B /15
0.4550844690444 = sin B
<B = 27.07
Now, <C = 180 - <A - <B = 180 - 55 - 27.07 = 98
Now, Using the Law of Sines
sin A/ a = sin C/ C
0.81915204428 / 27 = sin 98 / c
0.030338964602963 = 0.99026807 /c
c = 32.64
Learn more about Sine Law here:
https://brainly.com/question/13098194
#SPJ1
Find an equation of the plane that passes through the point (1, 2,3) and cuts off the smallest volume in the first octant. [This one is a little tricky.]
Answers
Answer and Step-by-step explanation:
Solution:
The equation is given by:
z – z0 = a(x – x0) + b(y – y0).
The point (1, 2, 3) is given , substitute them for x0, y0 and z0:
Z – 3 = a (x – 1) + b(y-2)
Both a and b should be negative, because normal vector to point in the negative x and y direction so that plane will enclose a tetrahedron with finite area in the first octant.
This will only happen if z becomes smaller as we move towards the positive x and y directions.
To find expressions for V, firstly find expression for x, y and z intercepts.
X – Intercepts (y and z = 0) : 2b +a -3 / a
y- Intercepts (x, z = 0): 2b + a- 3 / b
z – Intercepts( x, y = 0): 3 – a – 2b
The base is = (2b+a-3)2/ 2ab
Volume is 1/3 base x height, so
V (a, b) = - (2b+a-3)3 / 6ab
The gradient vector:
ΔV (a, b) = |- (3(2b+a-3)2 ab-b (2b+a-3)3)/6a2b2, (6(2b+a-3)2 ab-a(2b+a-3)3)/6a2b2| = 0
b (2b+a-3)2 [ (2b+a-3) -3a] = 0
a (ab + a-3)2 [(2b +a -3) – 6b] = 0
Where a, b not equal to 0.
We cannot solve for 2b +a-3 = 0 because, that will lead to V = 0, which is impossible.
Therefore, we only solve for second halves equations, which are system of linear equations:
-2a + 2b = 3 and a – 4b = 3
Which gives a = -3 and b = -3/2
Put in equation:
Z – 3 = -3 (x-1) – 3/2 (y-2)
3x +3/2 y +z = 9
Multiplying by 2:
6x + 3y + 2z = 18.
here is an inequality: -3x > 18 list some values for x that would make this inequality true
Answers
Step-by-step explanation: First, we need to solve this inequality.
When you're asked to solve an inequality like -3x > 18, your goal should be the same as it was when solving equations, to get x by itself on one side.
In this problem since x is being multiplied by -3 on the left side of the inequality, to get x by itself, we divide both sides by -3 but here is the rule you have to watch out for when solving inequalities.
When you divide both sides of an inequality by a negative number, you must switch the direction of the inequality sign. So this greater than in our original problem becomes less than in our second step.
On the left side, the -3's cancel and we're left with
x and on the right side, 18 divided by -3 is -6.
So we have x < -6.
Now, we are asked to state some solutions to the inequality.
The inequality x < -6 means that any number
less than -6 is a solution to the inequality.
For example, -7 is a solution because -7 is less than -6.
-8 is also a solution because -8 is less than -6.
Other possible solutions include -23, -98, -982, and so on.
Any number less than -6 will be a solution.
Match the numbers with the correct label.
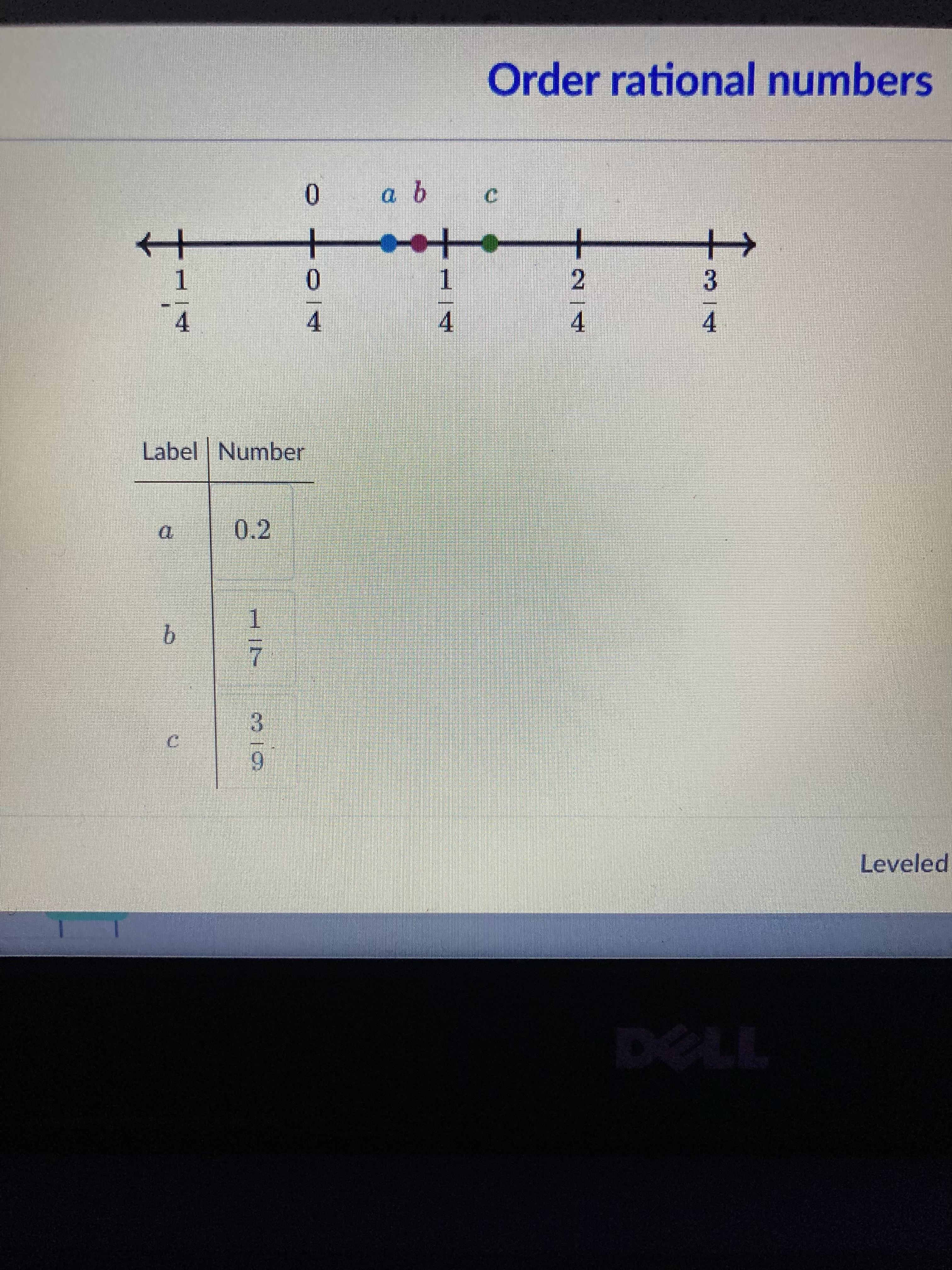
Answers
Answer:
a = 1/7b = 0.2c = 3/9Step-by-step explanation:
Converting all fractions to decimal (for easier comparison) :
0.21/7 = 0.143/9 = 0.33Hence,
First point (a) = 1/7Second point (b) = 0.2Third point (c) = 3/9The figure shows four box-and-whisker plots. These represent variation in travel time for four different types of transportation from the beginning to the end of one route.
Conrad is at one end of the route. He is trying to decide how to get to an appointment at the other end. His appointment is in 30 minutes. Which type of transportation is LEAST likely to take more than 30 minutes?
Select one:
a.
bus
b.
car
c.
subway
d.
train

Answers
Comparing the median of each box-and-whisker plot, the type of transportation that is LEAST likely to take more than 30 minutes is: d. train.
How to Interpret a Box-and-whisker Plot?
In order to determine the transportation that is LEAST likely to take more than 30 minutes, we have to compare the median of each data set represented on the box-and-whisker plot for each transportation.
The box-and-whisker plot that has the lowest median would definitely represent the the transportation that is LEAST likely to take more than 30 minutes, since median represents the typical minutes or center of the data.
Therefore, from the box-and-whisker plots given, the one for train has the lowest median. Therefore train would LEAST likely take more than 30 minutes.
Learn more about box-and-whisker plots on:
brainly.com/question/27849170
#SPJ1
If I had 60 units needed and units per case was 14 how many full cases and additional items are needed to fufill the order
Answers
60 units / 14 units per case ≈ 4.29 cases
Since you can't have a fractional number of cases, you would need to round up to the nearest whole number of cases. Therefore, you would need 5 full cases.
To determine the number of additional items needed to fulfill the order, you can subtract the number of units in the full cases from the total number of units:
60 units - (5 cases * 14 units per case) = 10 additional items
So, in total, you would need 5 full cases and 10 additional items to fulfill the order of 60 units.
What is the surface area of a box with a length of 6 ft, a width of 3 ft, and a height of 2½ ft?
Answers
Answer:
Step-by-step explanation:
Remark
The surface area is the area of all six sides when the object is a box.
Formula
SA = 2*L*w + 2*L*h + 2*w*h
Givens
L = 6 ft
w= 3 ft
h = 2.5 feet
Substitute and Solution
SA = 2*6*3 + 2*6*2.5 + 2*3*2.5
SA = 36 + 30 + 15
SA = 81
Oreana's 150 g bag of trail mix is x% raisins. Brandon's 250 g bag of trail mix is y% raisins. They combine the two mixes together in one bowl.
Write an expression which shows how many grams of raisins are in the bowl
Answers
The expression which shows how many grams of raisins are in the bowl will be
(0.01x) * 150 + (0.01y) * 250
What is the expression that shows the raisin?An expression is simply used to show the relationship between the variables that are provided or the data given regarding an information. In this case, it is vital to note that they have at least two terms which have to be related by through an operator. Some of the mathematical operations that are illustrated in this case include addition, subtraction, etc.
The expression which shows how many grams of raisins are in the bowl will be:
= (x% × 150) + (y% × 250)
= (0.01x) * 150 + (0.01y) * 250
This equation represents the total grams of raisins in the bowl by multiplying the weight of the Oreana's bag by the percentage of raisins in it, and adding that to the product of the weight of Brandon's bag and the percentage of raisins in it. The "0.01" is used to convert the percentages from x and y to decimal form.
Learn more about expressions on:
https://brainly.com/question/723406
#SPJ1
Three pizza are shared equally among 12 people.what fraction of a pizza will each person get?
A
4/1
B
3/1

Answers
Answer:
d) 1/12
Step-by-step explanation:
What happens if you can write a function as a composite in different ways? Do you get the same derivative each time? The Chain Rule says you should. Find
dy/dx if y=x by using the Chain Rule with y as a composite of the following functions. Complete parts (a) and (b) below.

Answers
Using the Chain Rule, we have: dy/dx = f'(g(x)) * g'(x) = 1 * 1 = 1.The derivative of y with respect to x is 1.
When we compose a function, it may be possible to write it in a variety of different ways. Differentiating such functions can result in different derivatives, but the Chain Rule indicates that the derivatives of the compositions should be the same regardless of how the function is written, if the function is continuous and differentiable.For instance, consider the function f(x) = sin(x²). It can be written as f(g(x)) where g(x) = x² and f(x) = sin(x). Furthermore, it can be written as f(h(x)) where h(x) = x² and f(x) = sin(x). These are both compositions of functions, but they are different compositions that lead to different derivatives.However, if the function is a composite of differentiable functions, the Chain Rule tells us that the derivative of a composite function is the derivative of the outer function multiplied by the derivative of the inner function.
To find dy/dx if y = x using the Chain Rule with y as a composite of the following functions, we must first rewrite y as a composite function: y = f(g(x)) where g(x) = x and f(x) = x. This composite function can be written in a variety of different ways, such as y = f(h(x)) where h(x) = x and f(x) = x, or y = f(k(x)) where k(x) = x and f(x) = x. However, regardless of how we write it, the Chain Rule tells us that the derivative of y is equal to the derivative of the outer function (f(x) = x) multiplied by the derivative of the inner function (g(x) = x).
For more such questions on derivative
https://brainly.com/question/26369159
#SPJ8
26. What 5-digit number has the following features:
If we put the numeral 1 at the beginning, we get a number three times smaller than if
we put the numeral 1 at the end of the number?
In other words, if you think the answer is the number 34567, then you want the
number 134567 to be one third of 345671, but it isn't, so what's the number?
Answers
The equation that represents ⨀A is (x+1)2+(y−1)2=16. Determine whether point B(3,1) is on the circle.
Answers
Answer:
Step-by-step explanation:
center=(-1,1)
radius=√16=4
distance between (-1,1) and (3,1)=√[(3+1)²+(1-1)²]=√[16+0]=√16=4=radius
Hence point lies on the circle.
The area of the floor of a cubical room is 49square meter. Find the area of 4 walls of room.
Answers
Answer:
If the walls are the standard 8 feet tall and the room is square, then:
the wall length and width is both 7 feet.
The area of the walls would be 4x7x8 = 224 ft² (also providing there are no doors or windows)
Read the sentence.
This is an example of a
Brendan is playing in the backyard.
O simple sentence.
O compound sentence.
O complex sentence.
O compound-complex sentence.
Answers
Answer:
I think it's simple sentence
Select all the points that are on the graph of the line:
2x + 4y=20

Answers
Answer:
B=10
Step-by-step explanation:
worked it out on a graph on the internet
20 points!!Use what we know about the pythagorean theorem
to determine if this triangle is a right triangle. Write a
statement explaining why this is or is not a right
triangle. Show your work to justify your answer.

Answers
The triangle is a not right triangle because it does not follow the Pythagoras theorem
How to determine if the triangle is a right triangle?From the question, we have the figure that represents the parameter that can be used in our computation:
The sides of the triangles are
6, 8 and 9
For a triangle to be a right triangle, the side lengths must follow the Pythagoras theorem
The Pythagoras theorem states that
Longest side² = Sum of the squares of the other sides
So, we have
9² = 6² + 8²
Evaluate
81 = 100
The above equation is false
Hence, the triangle is not a right triangle
Read more about right triangle at
https://brainly.com/question/2437195
#SPJ1
many solutions or no solutions -2(x-2)-4x=3(x-1)-9x
Answers
∑ Hey, claudiavg2000 ⊃
Answer:
No solutions.
Step-by-step explanation:
Given:
-2(x-2)-4x=3(x-1)-9x
Solve:
-2 ( x - 2 ) - 4x : -6x + 4
3(x - 1) - 9x : -6x - 3
Now we have;
-6x + 4 = -6x - 3
Subtract 4 from both sides:
-6x + 4 - 4 = -6x - 3 - 4
-6x = -6x -7
Add 6x to both sides:
-6x + 6x = -6x - 7 + 6x
Simplifying:
0 = -7
As you can see the sides are not equal.
Hence, This problem has no solution.
xcookiex12
8/18/2022
Is this correct if not can someone give me the answer I will mark u brilliant

Answers
Answer: the first one is 735.75
the second one is 69
Step-by-step explanation:
THEY ARE BOTH CORRECT!
Answer: They are both correct. Good job! :)
Step-by-step explanation:
A metalworker has a metal alloy that is 15% copper and another alloy that is 70% copper. How many kilograms of each alloy should the metalworker combine to create 80 kg of a
48% copper alloy?
The metalworker should use kilograms of the metal alloy that is 15% copper and kilograms of the metal alloy that is 70% copper
(Type whole numbers.)
Answers
Answer:
18 kg of 15% copper alloy
62 kg of 70% copper alloy
Step-by-step explanation:
Step 1: Calculate the total amount of copper present in 80 kg of 48% copper alloy
Total Copper = 80 x 0.48 = 38.4 kg
Step 2: Calculate the amount of 15% copper alloy required
15% Copper Alloy = 38.4 / 0.15 = 256 kg
Step 3: Calculate the amount of 70% copper alloy required
70% Copper Alloy = (80 - 256) = -176 kg
Step 4: Since the amount of 70% copper alloy required is negative, the metalworker should use 256 kg of the 15% copper alloy and 0 kg of the 70% copper alloy to create 80 kg of 48% copper alloy.
Please help answer my question

Answers
Answer:
x = 6
Step-by-step explanation:
This is a bit of a tricky equation, and it's what we call an exponential equation since it involves some exponents. The way we begin to solve these kinds of problems is make the base on each side of the equals sign the same. On one side, we have 9 as our base, and on the other side, we have 3 as our base. 9 = 3², so we can rewrite our equation as shown below:
(3²)⁴ˣ⁻¹⁰ = 3⁵ˣ⁻²
From there, we can use the exponent rule (xᵃ)ᵇ = xᵃᵇ to simplify the left side of the equation.
3²⁽⁴ˣ⁻¹⁰⁾ = 3⁵ˣ⁻²
3⁸ˣ⁻²⁰ = 3⁵ˣ⁻²
Since our bases are now the same, we can take just the exponents and turn it into a new equation as shown below:
8x - 20 = 5x - 2
Hopefully at this point, this problem becomes easy for you, but I'll show how I solved this new equation below in case it doesn't make sense.
8x - 20 = 5x - 2
8x - 20 - 5x = 5x - 2 - 5x
3x - 20 = -2
3x - 20 + 20 = -2 + 20
3x = 18
3x/3 = 18/3
x = 6
Hopefully that's helpful! Let me know if you need more help. :)
9(2n+1) help please brooooooo
Answers
Answer:
18n + 9
Step-by-step explanation:
Distribute 9 into the expression.
9*2n = 18n
9*1 = 9
18n + 9
5a. find the value of a.

Answers
The logarithmic function f(x) = a·log₃(x - 4), passing through the points (13, 7), has the values;
5 a. The value of a is 3.5
b. Please find attached the graph of the function, f(x) = 3.5·log₃(x - 4), created with MS Excel
What is a logarithmic function?A logarithmic function is a function that contain and involves logarithm operation and it is the inverse of an exponential function
The function is f(x) = a·log₃(x - 4),
x > 4 and a > 0
The coordinates of a point on the graph of the function, f is A(13, 7)
5 a. The value of a can be found by plugging in the value of (13, 7) = (x, f(x)), as follows
f(13) = 7 = a·log₃(13 - 4) = a·log₃9 = a·log₃3²
7 = a·log₃3²
7 = 2·a·log₃3 = 2·a·1 = 2·a
2·a = 7
a = 7 ÷ 2 = 3.5
a = 3.5
5 b. The coordinates of the x-intercept of the graph = (5, 0)
The equation of the function is;
f(x) = 3.5·log₃(x - 4)
A third point on the graph is given when f(x) = 14 as follows;
f(x) = 14 = 3.5·log₃(x - 4)
log₃(x - 4) = 14 ÷ 3.5 = 4
3⁴ = x - 4
x = 3⁴ + 4 = 85
Which gives the point, (85, 14)
Similarly, we have the point (31, 10.5), (7, 3.5)
Please find attached the graph of f(x) created with MS Excel
Learn more about logarithmic functions here:
https://brainly.com/question/28033379
#SPJ1

20 drops = _______ teaspoon
Please help ASAP!
Answers
Answer:
76
Step-by-step explanation:
Answer:
0.2
Step-by-step explanation:
Please help me with this it is very important to my grade

Answers
Answer:
Option B is correct
Step-by-step explanation:
\( \sf \longmapsto \: \frac{{x}^{3} - {y}^{3} }{4} \\ \sf \longmapsto \: \frac{ {4}^{3} - {2}^{3} }{4} \\ \sf \longmapsto \: \frac{64 - 8}{4} \\ \sf \longmapsto \: \frac{56}{4} \: \: \: \: \: \: \: \: \\ \sf \longmapsto \: 14\)
HELP! HELP! HELP! HELP!:

Answers
Answer:b
Step-by-step explanation:
Answer:
c number is correct
Step-by-step explanation:
there is h-6= 10
the minus in six after going to other side makes the sign change into +
Please help answer this
