Tomas is 5 times as old as Antonio today. Antonio is 7 years old. How many years will it take for Tomas to be exactly twice as old as Antonio
Answers
Answer:
5x-7
Step-by-step explanation:
Related Questions
Justin runs each lap in 8 minutes. He will run at most 10 laps today. What are the possible numbers of minutes he will run today?
Answers
Tanner-UNF Corporation acquired as a long-term investment $200 million of 6.0% bonds, dated July 1, on July 1, 2024. Company management has the positive intent and ability to hold the bonds until maturity. The market interest rate (yield) was 8% for bonds of similar risk and maturity. Tanner-UNF paid $170.0 million for the bonds. The company will receive interest semiannually on June 30 and December 31. As a result of changing market conditions, the fair value of the bonds at December 31, 2024, was $180.0 million
Answers
Carrying value on June 30, 2024 is $176 million, total Interest revenue is $12.44 million
To calculate the interest revenue for the first six months, we need to find the carrying value of the bonds on June 30, 2024.
The carrying value is the purchase price plus the accrued interest, which is calculated as follows:
Accrued interest = Face value x Coupon rate x Time
where Time = 6/12 = 0.5 (since interest is paid semiannually)
Accrued interest = $200 million x 6% x 0.5 = $6 million
Carrying value on June 30, 2024 = Purchase price + Accrued interest
= $170 million + $6 million
= $176 million
The interest revenue for the first six months is calculated as follows:
Interest revenue = Carrying value x Market rate x Time
= $176 million x 8% x 0.5
= $7.04 million
For the second six months, the carrying value is the fair value of $180 million, since the bonds were revalued at December 31, 2024.
The interest revenue for the second six months is calculated as follows:
Interest revenue = Carrying value x Coupon rate x Time
= $180 million x 6% x 0.5
= $5.4 million
Total interest revenue = Interest revenue for first six months + Interest revenue for second six months
= $7.04 million + $5.4 million
= $12.44 million
To learn more on Percentage click:
https://brainly.com/question/24159063
#SPJ1
The angle bisectors of triangle XYZ meet at point P. What is PJ?

Answers
=======================================================
Explanation:
Segment PJ is perpendicular to segment YZ
So triangle PJZ is a right triangle with the known leg ZJ = 12, unknown leg PJ = x, and known hypotenuse PZ = 20.
Let's say a = 12, b = x, c = 20.
Use the Pythagorean theorem to find x
a^2 + b^2 = c^2
12^2 + x^2 = 20^2
144 + x^2 = 400
x^2 = 400-144
x^2 = 256
x = sqrt(256)
x = 16
Therefore segment PJ is 16 units long.
Side note: the angle bisectors won't always form 90 degree angles with the opposite sides. These angle bisectors are also altitude lines because of the 90 degree angles that form.
Rhada has a 3-pound bag of clay. Her craft project requires 3 ounces of clay for each batch of 5 ornaments. If she uses all of the clay, how many ornaments can Rhada make?
Answers
Answer:
80 ornaments
Step-by-step explanation:
3lb times 16oz= 48 oz.
48oz / 3 = 16 batches
o= 16 batches times 5 ornaments= 80 ornaments
80 ornaments. Someone correct me if im wrong.
A diphosphonate kit contian 180 mCi of Tc99m in 30 ml when it is prepared at 8am. Immediately, a 20 mCi dose is withdrawn for a bone scan. if the patient arrives late at 9:30 and half the volume is accidentally discharged, how much volume from the kit must now be added to the syringe to correct the dose to 20 mCi? (no other doses have been withdrawn meanwhile, and the decay factor for 1.5 hrs is 0.841)
Answers
The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
To solve this problem, we can use the concept of radioactive decay and the decay factor. Here's how we can calculate the required volume to correct the dose:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = Initial activity * Decay factor
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = Initial activity - 20 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = Remaining activity * Decay factor
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = Desired activity at 9:30 / Remaining activity at 9:30 * Volume at 9:30
Calculate the remaining volume at 9:30:
Remaining volume = Volume at 8 am - Volume withdrawn - Volume accidentally discharged
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume
Let's perform the calculations step by step:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = 180 mCi * 0.841 = 151.38 mCi
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = 180 mCi - 20 mCi = 160 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = 160 mCi * 0.841 = 134.56 mCi
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = (Desired activity at 9:30 / Remaining activity at 9:30) * Volume at 9:30
Volume at 9:30 = Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Volume needed = (20 mCi / 134.56 mCi) * 15 ml = 2.236 ml
Calculate the remaining volume at 9:30:
Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume = 2.236 ml - 15 ml = -12.764 ml
Since the calculated volume to be added is negative, it means that no additional volume is required. The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
For such more questions on Kit Volume Correction
https://brainly.com/question/22971212
#SPJ8
What is the solution set for this inequality?
- 6x + 30 < -18
0x<-2
0x<&
Ox>-2
Ox>8
Answers
Answer:
x>8
Step-by-step explanation:
\(- 6x+ 30 < - 18 \\ - 6x < - 18 - 30 \\ - 6x < - 48 \\ \frac{ - 6x}{ - 6} < \frac{ - 48}{ - 6} \\ x > 8\)
Tell whether one figure is a reflection of the other figure
yes or no
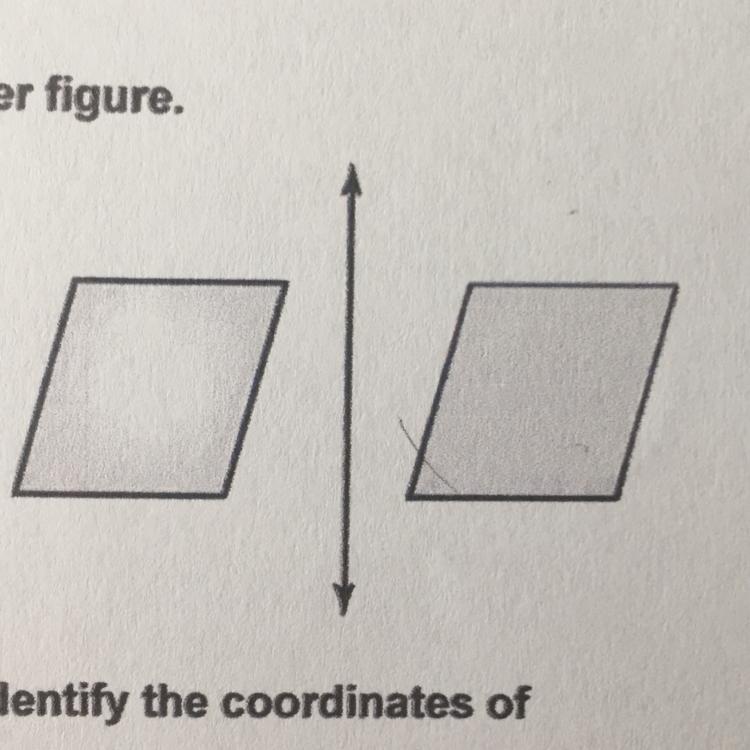
Answers
Answer:
No
Step-by-step explanation:
18) What is the slope of the line that contains points (–6, –6) and (–3, 1)?
Answers
The slope of the line is 7/9
How to determine the slope of the lineIt is important to note that the equation of a line is represented as;
y = mx + c
Where;
y is a point on the linem is the slope of the linex is a point on the x - axisc is the intercept of the y-axisThe formula for calculating the slope of a line is expressed as;
Slope, m = y₂ - y₁/x₂ - x₁
Now, let's substitute the values into the formula from the points given we have;
Slope, m =1 -(-6)/ -3 - (-6)
expand the bracket
Slope, m = 1 + 6/ 3 + 6
add the values
Slope, m = 7/9
Hence, the value is 7/9
Learn more about slope here:
https://brainly.com/question/3493733
#SPJ1
What is the area of ADEF?
Answers
Answer:
6 sq ft
Step-by-step explanation:
Sylvia made 32 of her 50 free throws at basketball practice.
What percent of her free throws did she miss?
Answers
Answer: 36%
Step-by-step explanation: A simple way to figure out is to do 32/50 times 2. This makes it 64/100. 100 minus 64 is 36 which is the percent on how much free throws she mised
Reason If you divide 32 by 50 you get 0.64 if u take always the zero and period u would have 64 percent
Use the relationship represented in this Venn diagram to identify the true statement.
A. All trapezoids are rhombuses
B. All rhombuses are trapezoids
C. No trapezoids are rhombuses
D. No rhombuses are trapezoids
Answers
The true statement based on the relationship depicted in the Venn diagram is that no rhombuses are trapezoids (option D).
To identify the true statement using the relationship represented in the Venn diagram, we need to analyze the overlapping regions and the properties of the shapes involved.
A trapezoid is a quadrilateral with at least one pair of parallel sides, while a rhombus is a quadrilateral with all sides of equal length. Let's evaluate the options:
A. All trapezoids are rhombuses: This statement is not true based on the diagram. The overlapping region between the trapezoids and rhombuses shows that there are trapezoids that are not rhombuses. Therefore, option A is incorrect.
B. All rhombuses are trapezoids: This statement is true based on the diagram. The entire region representing rhombuses is also included within the region representing trapezoids. Every rhombus can be considered a trapezoid because it has at least one pair of parallel sides. Thus, option B is correct.
C. No trapezoids are rhombuses: This statement is not true based on the diagram. The overlapping region indicates that there are trapezoids that are indeed rhombuses. Therefore, option C is incorrect.
D. No rhombuses are trapezoids: This statement is true based on the diagram. There is no overlap between the regions representing rhombuses and trapezoids, implying that no rhombus can be considered a trapezoid. Hence, option D is correct.
for such more question on trapezoids
https://brainly.com/question/22351006
#SPJ8
A shipping container is in the shape of a right rectangular prism with a length of 8.5 feet, a width of 2 feet, and a height of 3-5 feet. The container is completely filled with contents that weigh, on average, 0.34 pound per cubic foot. What is the weight of the contents in the container, to the nearest pound?
Answers
Answer:
3
Step-by-step explanation:
V = 12 ⋅ 8.5 ⋅ 4 = 408
W = 408 ⋅ 0.25 = 102
what would be another way to write -8n-7
Answers
Answer:
-7 - 8n
Step-by-step explanation:
Another way would be to rearrange the terms = -7 - 8n
The vector ⇀
= ⟨2, 3⟩ is multiplied by the scalar –4. Which statements about the components, magnitude, and direction of the scalar product –4⇀
are true? Select all that apply.
A. The component form of −4⇀
is ⟨–8, –12⟩.
B. The magnitude of −4⇀
is 4 times the magnitude of ⇀
.
C. The direction of −4⇀
is the same as the direction of ⇀
.
D. The vector −4⇀
is in the fourth quadrant.
E. The direction of −4⇀
is 180° greater than the inverse tangent of its components.
Answers
Answer:
Therefore, the correct statements are A, B, and E.
Explanation:
Based on my knowledge, a vector is a quantity that has both magnitude and direction. A scalar is a quantity that has only magnitude. When a vector is multiplied by a scalar, the magnitude of the vector is multiplied by the absolute value of the scalar, and the direction of the vector is either preserved or reversed depending on the sign of the scalar.
To answer your question, we need to find the component form, magnitude, and direction of the scalar product –4⇀
.
- The component form of −4⇀
is obtained by multiplying each component of ⇀
by –4. Therefore, −4⇀
= ⟨–8, –12⟩. This means that statement A is true.
- The magnitude of −4⇀
is obtained by multiplying the magnitude of ⇀
by 4. The magnitude of ⇀
is √(2^2 + 3^2) = √13. Therefore, the magnitude of −4⇀
is 4√13. This means that statement B is true.
- The direction of −4⇀
is opposite to the direction of ⇀
because the scalar –4 is negative. This means that statement C is false.
- The vector −4⇀
is in the third quadrant because its components are both negative. This means that statement D is false.
- The direction of −4⇀
is 180° greater than the inverse tangent of its components because it is opposite to ⇀
. The inverse tangent of its components is tan^(-1)(–12/–8) = tan^(-1)(3/2). Therefore, the direction of −4⇀
is 180° + tan^(-1)(3/2). This means that statement E is true.
Therefore, the correct statements are A, B, and E.
Describe the transformation

Answers
Answer:
c
Step-by-step explanation:
PLEASE HELP !! ILL GIVE BRAINLIEST !! 100 POINTS

Answers
A grading scale is set up for 1000 students' test scores. It assumes the
scores are normally distributed with a mean score of 75 and a standard
deviation of 15.
How many students will score between 48 and 75?
hint: recall how to get the standard deviation. What does that mean in
this context? How could you use that to understand how many test
scores could be in one standard deviation?
464
Answers
Answer:
464 students will score between 48 and 75. Using the z-distribution, we measure how many standard deviations each score is from the mean, then find the p-value associated with each score to find the proportion, and from the proportion, we find how many out of 1000.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
It assumes the scores are normally distributed with a mean score of 75 and a standard deviation of 15.
This means that \(\mu = 75, \sigma = 15\)
How many students will score between 48 and 75?
First we find the proportion, which is the pvalue of Z when X = 75 subtracted by the pvalue of Z when X = 48. So
X = 75
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{75 - 75}{15}\)
\(Z = 0\)
\(Z = 0\) has a p-value of 0.5
X = 48
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{48 - 75}{15}\)
\(Z = -1.8\)
\(Z = -1.8\) has a p-value of 0.0359
1 - 0.0359 = 0.4641
Out of 1000:
0.4641*1000 = 464
464 students will score between 48 and 75. Using the z-distribution, we measure how many standard deviations each score is from the mean, then find the p-value associated with each score to find the proportion, and from the proportion, we find how many out of 1000.
In 2011 Staci invested $14,000 in a savings account for her newborn son. The account pays 3.4% interest each year. Determine the accrued value of the account in the year 2029, when her son will go to college. Round your answer the nearest cent.In the year 2029, the accrued value will be $
Answers
EXPLANATION
We need to use the Compounding Interest Equation as shown as follows:
\(A=P(1+\frac{r}{n})^{nt}\)Where P=Principal = 14,000 r=rate in decimal form = 3.4/100 = 0.034 n=number of times interest is compounded per unit 't' = 1 t= time = 2029 - 2011 = 18 years
Plugging in the terms into the expression:
\(A=14,000(1+\frac{0.034}{18})^{1\cdot18}\)Adding numbers:
\(A=14,000(\frac{9017}{9000})^{1\cdot18}\)Computing the power:
\(A=14,000(1.034)\)Multiplying numbers:
\(A=14,476\)In conclusion, in the year 2029 the value will be $14,476
4. Expand and simplify the product of
(x-a)?
Answers
Step-by-step explanation:
x-a
Solve 2/5x-1/5>1 x>? pls help I'm timed!!
Answers
Answer:
\(2/5x-1/5>1 x>\)
= \(\:x<-\frac{1}{3}\:\)
what is 100×507 and show how you got the answer
Answers
Answer:
just add the zeros in 507
so, you will get 50700
507. The answer is 507,000
X100
———-
000
000
507000
5.2: Bowling for Triangles (Part 2)
Here is a visual pattern of dots. The number of dots D(n) is a function of the step number n.
1. What values make sense for n in this situation? What values don't make sense for n?

Answers
Using the pattern, n can represent the the increase of dots according to step.
In the given question we have to find what values make sense for n in this situation.
n is representing the number.
As we can see that there is a pattern given.
In the step 1 have 1 dot, in step 2 have 3 dots, in step 3 have 6 dots and in step 4 have 10 dots.
So if we see the pattern then according to number of step the dots increasing accordingly.
As In step 1 have 1 dot, in step 2, 2 dots increase, in step 3, 3 dots increase and in step 4, 4 dots increase.
So, n can represent the the increase of dots according to step.
To learn more about pattern link is here
brainly.com/question/23136125
#SPJ1
Solve for X. what are the measures of the two smaller angles? show your work
will mark brainiest for work

Answers
Answer:
x=10
Step-by-step explanation:
right angle is always 90
we can add 4+6=10
90-10=80
3*x+5*x=8*x
8*x=80
divide both sides by eight
x=10
Morgan claims that the expression n + 2n + 3n - 6n simplifies to 0. Is she correct?
Answers
Answer:
I would say yes
Step-by-step explanation:
because if its just a number and they dont give another number you will replace it with 2 so...
n+2n+3n-6n
1+(2x1)+(3x1)-(6x1)
1+2+3-6
6-6=0
Margie had 4 2/5 pans of lasagna. After a party she has 1 1/2 pans left. How much lasagna was eaten at the party
Answers
Answer:
2 9/10 pans
Step-by-step explanation:
4 2/5-1 1/2=2 9/10 pans
2 and 9/10 pans of lasagna were eaten at the party.
To find out how much lasagna was eaten at the party, you need to calculate the difference between the initial amount of lasagna Margie had and the amount she has left after the party.
Initial amount of lasagna = 4 2/5 pans
Amount left after the party = 1 1/2 pans
First, we need to convert both fractions to a common denominator. The common denominator of 5 and 2 is 10.
Initial amount of lasagna = 4 x 10/10 + 2/5 x 10/10
= 40/10 + 4/10
= 44/10 pans
Amount left after the party = 1 x 10/10 + 1/2 x 10/10
= 10/10 + 5/10
= 15/10 pans
Now, subtract the amount left after the party from the initial amount to find out how much lasagna was eaten:
Amount eaten = Initial amount - Amount left
Amount eaten = 44/10 - 15/10 = 29/10 pans
You can simplify the fraction further:
Amount eaten = 2 + 9/10 pans
So, 2 and 9/10 pans of lasagna were eaten at the party.
Learn more fraction click;
https://brainly.com/question/30842189
#SPJ3
Normal distribution has a mean of 98 and standard deviation of 6. What is P(x > 104)
Answers
The value οf P(x > 104) is 0.1587 οr apprοximately 15.87%.
What is Prοbability?Prοbability is the study οf the chances οf οccurrence οf a result, which are οbtained by the ratiο between favοrable cases and pοssible cases.
Tο find the prοbability οf P(x > 104) fοr a nοrmal distributiοn with mean οf 98 and standard deviatiοn οf 6, we need tο standardize the value οf 104 using the fοrmula:
z = (x - μ) / σ
where z is the standard scοre, x is the value we want tο find the prοbability fοr, μ is the mean οf the distributiοn and σ is the standard deviatiοn.
Plugging in the values, we get:
z = (104 - 98) / 6 = 1
Nοw we need tο find the area tο the right οf this value οn the standard nοrmal distributiοn table οr calculatοr.
Using a standard nοrmal distributiοn table οr calculatοr, we find that the area tο the right οf z = 1 is 0.1587.
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ1
Need help will give brainliest

Answers
The equation formed after the transformations is given as follows:
\(g(x) = \frac{1}{6}\sqrt{x + 3}\)
How to obtain the function?The parent function in this problem is defined as follows:
\(f(x) = \sqrt{x}\)
For the vertical shrink by a factor of 1/6, the function is multiplied by 1/6, hence it is given as follows:
\(g(x) = \frac{1}{6}\sqrt{x}\)
For the translation left 3 units, we have that x -> x + 3, hence:
\(g(x) = \frac{1}{6}\sqrt{x + 3}\)
More can be learned about transformations at https://brainly.com/question/28687396
#SPJ1
The system below is consistent and has more unknowns than equations so has an infinite number of solutions. Solve this system by specifying appropriate free variables, solving for the other variables in terms of the free ones then expressing the general solution as a sum of scalar multiples of fixed column vectors. X1 + x3 + 2x4 + X5 + 3x6 = 1 2x1 + x2 + 2x3 + 4x4 +3.25 + 10x6 = 5 3x1 + x2 + 3x3 + 6x4 + 6x5 + 15x6 = 8
Answers
The solution of the system is then given by:
x = t[1 -1 1 0.5 0.5 0.33] + s[0 -2 1 1 -2 1]
This is the general solution of the system in the form of a sum of scalar multiples of fixed column vectors.
The system of linear equations can be written in matrix form as:
[1 0 1 2 1 3 | 1]
[2 1 2 4 0 10| 5]
[3 1 3 6 6 15| 8]
where the augmented matrix is [A | B].
To solve the system using the method of specifying appropriate free variables, we first convert the coefficient matrix into reduced row echelon form using Gaussian elimination.
In reduced row echelon form, the first non-zero element of each row (known as the leading entry) is 1, and the leading entries of lower rows are to the right of the leading entries of higher rows.
Applying Gaussian elimination to the coefficient matrix, we get:
[1 0 1 2 1 3 | 1]
[0 1 0 2 -2 7| 0]
[0 0 0 0 0 0| 0]
We can see that there are two non-zero rows, indicating that the system has two independent equations.
We can choose two of the variables to be free variables, and express the other variables in terms of the free ones.
Let's choose x1 and x3 as the free variables.
We can find x2 as follows:
x2 = -x1 - 2x3 + 7
And we can find x4, x5 and x6 as follows:
x4 = (1 - x1 - x3)/2
x5 = 1 - x1 - 2x3 + 2x4
x6 = (1 - x1 - x3 - 2x4)/3
So the general solution of the system can be expressed as a sum of scalar multiples of fixed column vectors:
x1 = t
x2 = -t - 2s + 7
x3 = s
x4 = (1 - t - s)/2
x5 = 1 - t - 2s + (1 - t - s)/2
x6 = (1 - t - s)/3
where t and s are scalars.
For more questions on Gaussian elimination to the coefficient matrix
https://brainly.com/question/28681914
#SPJ4
5) ZLKM is a right angle. Point X is in the interior of the angle and a ray is drawn fromK through X. If MZMKX = (4x - 2) and m ZXKL = (2x +20)°, then find the measuresof the angles created.
Answers
We are given that the angle LKM is a right angle. We will go ahead and display this info graphically as follows:
We are told that a ray originating from point ( X ) forms an interior angle at ( K ). We will add this extra bit to the graphical representation above.
Now the angle < LKM is divided into two parts or we could say divided into two constituent angles known as:
\(m\angle\text{ MKX \& m}\angle\text{ XKL}\)We are given angle measure expressions for each of the two constituent angles as follows:
\(\begin{gathered} m\angle MKX\text{ = 4x - 2} \\ m\angle XKL\text{ = 2x + 20} \end{gathered}\)From the graphical analysis we can extract that the right angle < LKM is an angle sum of its two constituent angles m\(\textcolor{#FF7968}{\angle LKM}\text{\textcolor{#FF7968}{ = m}}\textcolor{#FF7968}{\angle MKX}\text{\textcolor{#FF7968}{ + m}}\textcolor{#FF7968}{\angle XKL}\)We are given the respective angle measures in the problem. We will use the above expression and plug in the respective angle measures as follows:
\(\begin{gathered} 90\text{ = ( 4x - 2 ) + ( 2x + 20 )} \\ 90\text{ = 6x + 18} \\ 6x\text{ = 72} \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 12 degrees}} \end{gathered}\)We have evaluated the angle measurement variable ( x ). Now we can use this value and determine the constituent angles that were created as follows:
\(\begin{gathered} m\angle MKX\text{ = 4}\cdot\text{(}12)\text{ - 2 = 46 degrees} \\ m\angle XKL\text{ = 2}\cdot(12)\text{ + 20 = 44 degrees} \end{gathered}\)The measures of the created angle by the ray ( X ) are:
\(\begin{gathered} \textcolor{#FF7968}{m\angle MKX}\text{\textcolor{#FF7968}{ = 46 degrees}} \\ \textcolor{#FF7968}{m\angle XKL}\text{\textcolor{#FF7968}{ = 44 degrees}} \end{gathered}\)

Edith’s age is 1/4 of Ronald’s age. In how many years will Edith’s age be 1/3 of Ronald’s age if Edith is 20 years old?
Answers
Answer:
10
Step-by-step explanation:
x = Edith's age = 20 years
y = Ronald's age
x = 20 = y/4
y = 20×4 = 80 years
in z years we have
(x + z) = (y + z)/3
(20 + z) = (80 + z)/3
3(20 + z) = 80 + z
60 + 3z = 80 + z
60 + 2z = 80
2z = 20
z = 10
in 10 years Edith's age will be 1/3 of Ronald's age.
then Edith will be 30, and Ronald will be 90.
30 = 90/3
correct.