The point (-1, 5) ___ (is or is not) on the parabola because the point is ___ units from the directrix and ___ units from the focus.
The point (3, 3) (is or is not) on the parabola because the point is ___ units from the directrix and ___ units from the focus
The point (5,5) (is or is not) on the parabola because the point is ___ units from the directrix and ___ units from the focus

Answers
For the point (5, 4) to the directrix, the distance to the directrix is equal to the distance to the focus. For the other points on the list, the distance to the directrix is equal to the distance to the focus. The distance to the directrix is equal to the distance to the focus, we can conclude that (-1, 5) is on the parabola.
What is parabola ?A perfect, U-shaped curve is referred to by the term parabola in mathematics. It is described as the collection of all plane points that are equidistant from a focus and a fixed broadband (the directrix). The point where the parabola's curve changes direction is known as its vertex, and the line that runs through it and is perpendicular toward the directrix is known as its axis of symmetry. The behavior of electromagnetic waves, projectile motion, reflector and antenna forms, and other real-world phenomena are frequently modelled using parabolas.
To determine whether a point is on a parabola with a given focus and directrix, we can use the definition of a parabola: a parabola is the set of all points that are equidistant to the focus and the directrix.
In this case, the focus is the point (0, 2) and the directrix is the line y = -2.
Let's first consider the point (5, 4). We can find the distance from this point to the directrix by finding the distance from the point to the line. The formula for the distance from a point (x1, y1) to a line \(Ax + By + C = 0\) is:
\(|Ax1 + By1 + C| / \sqrt(A^2 + B^2)\)
In this case, A = 0, B = 1, and C = -2, so the equation of the directrix is y = -2, which can be written as \(0x + 1y - 2 = 0.\) Plugging in (5, 4), we get:
\(|0(5) + 1(4) - 2| / \sqrt(0^2 + 1^2) = 6\)
So the distance from (5, 4) to the directrix is 6.
Next, we can find the distance from (5, 4) to the focus (0, 2):
\(\sqrt((5-0)^2 + (4-2)^2) = \sqrt(29)\)
Since the distance from (5, 4) to the directrix is not equal to the distance from (5, 4) to the focus, we can conclude that (5, 4) is not on the parabola.
We can repeat this process for each point on the list. For the point (-1, 5), we get:
Distance to directrix: |-1 - 2| / 1 = 3
Distance to focus: \(\sqrt((-1-0)^2 + (5-2)^2) = \sqrt(26)\)
Since the distance to the directrix is equal to the distance to the focus, we can conclude that (-1, 5) is on the parabola.
Similarly, we can check the other points on the list and find that the points (4, 3), (2, 1), (1, -2), (2, -1), (4, -3), and (5, -4) are also on the parabola. The points (3, 5), (6, 7), (8, 0), and (0, 8) are not on the parabola.
To know more about parabola visit :-
brainly.com/question/4074088
#SPJ1
Related Questions
plssssss help i really dont get his :/

Answers
Answer:
Step-by-step explanation:
1 1/8
16 2
20 2.5
24 3
The value next to one indicates the conversion between a quarter and a toonie. 1 quarter is worth to 1/8 of a toonie
A home goods store purchased a desk lamp and marked it up 155% from the original cost of $9.12. Then, wanting to make room for summer inventory, the store placed the desk lamp on sale for 30% off. What was the price after the discount?
Answers
Answer:
16.28 Dollars
Step-by-step explanation:
Hope this helps! :)
does the data provide evidecnet htat there isa. linear association between hours of telvision watched a week an dgpa?
Answers
Yes, the data provide evidence that there is a linear association between hours of television watched a week and GPA. This statement can be supported by statistical analysis of the data.
What is a linear association?A linear association exists between two variables when the pattern of their plotted values on a scatterplot approximates a straight line. A linear association occurs when one variable increases while the other decreases. It is also known as a straight-line relationship.
The data you have asked about, which is the relationship between hours of television watched a week and GPA can be analyzed using statistical tools. The data can be graphed in a scatterplot to see whether there is a pattern between the variables. If a straight-line pattern is observed, then there is a linear association.
The statistical tools that can be used to analyze the data include the calculation of the correlation coefficient and regression analysis. The correlation coefficient is a measure of the strength of the association between two variables. It ranges from -1 to 1, with -1 indicating a perfect negative relationship, 0 indicating no relationship, and 1 indicating a perfect positive relationship.
Regression analysis can be used to determine the equation of the line of best fit for the data. This line represents the linear relationship between the two variables. By analyzing the slope of the line, we can determine the strength of the relationship between the variables. In conclusion, yes, the data provide evidence that there is a linear association between hours of television watched a week and GPA.
Learn more about Linear association:
https://brainly.com/question/20257865
#SPJ11
NEED HELP ASAP. please do not answer if you won’t help. If three resistors with resistances R1,R2,R3, are connected in parallel their combined resistance R is given by formula R. Will give brainliest if helpful

Answers
= 1/ (R2R3 + R1R3 + R1R2)/R1R2R3
= R1R2R3/ (R2R3 + R1R3 + R1R2)
A radioactive substance decays exponentially. A scientist begins with 200 milligrams of a radioactive substance. After 22 hours, 100 mg of the substance remains. How many milligrams will remain after 32 hours?A radioactive substance decays exponentially. A scientist begins with 200 milligrams of a radioactive substance. After 22 hours, 100 mg of the substance remains. How many milligrams will remain after 32 hours?
Answers
76.74 milligrams will remain after 32 hours.
What is a radioactive substance?N(t) = N₀e^(-kt)
where:
N(t) is the amount of substance remaining after time t
N₀ is the initial amount of substance
k is the decay constant
To solve for the decay constant, use the information given in the problem:
100 = 200e^(-22k)
Dividing both sides by 200, we get:
0.5 = e^(-22k)
Taking the natural logarithm of both sides, we get:
ln(0.5) = -22k
Solving for k, we get:
k = ln(0.5)/(-22) = 0.0316
Use this value of k to find the amount of substance remaining after 32 hours:
N(32) = 200e^(-0.0316*32) = 76.74 mg
Therefore, approximately 76.74 milligrams of the substance will remain after 32 hours.
Learn more about radioactive decay, here:
https://brainly.com/question/1770619
#SPJ1
76.4 milligrams will remain after 32 hours.
Define the term exponential?Exponential refers to a mathematical function in which a constant base is raised to a variable exponent. The value of the function increases or decreases rapidly as the exponent increases, depending on whether the base is greater than 1 or between 0 and 1. Exponential functions are commonly used to model situations where a quantity grows or decays at a constant percentage rate over time.
What is decay?Decay is the natural process of deterioration or rotting of a substance over time. It can occur in both organic and inorganic materials and is often caused by the activity of microorganisms, exposure to oxygen or other environmental factors.
To determine the amount of radioactive substance that remains after 32 hours, we can use the formula A = A₀ ×\(e^{-kt}\), where A is the amount remaining, A₀ is the initial amount, k is the decay constant, and t is the time elapsed.
we can use the same formula for exponential decay to find the value of k:
100 = 200 × \(e^{(-k*22)}\)
0.5 = \(e^{(-k*22)}\)
ln(0.5) = -k×22
k = ln(2)/(22)
Now we can use this value of k to find the amount of substance remaining after 32 hours:
N(32) = 200 \(e^{(-k*32)}\)
N(32) = 200 \(e^{(-(ln(2)/(22))32)}\)
N(32) ≈ 76.4 mg
Therefore, approximately 76.4 milligrams of the substance will remain after 32 hours.
Learn more about function here:
https://brainly.com/question/12431044
#SPJ1
A baseball player had 4 hits in 8 games. At this rate, how many hits will the baseball player have in the next 28 games?
Answers
4/8 = .5
28 x .5 = 14
He will hit about 14 balls in the next 28 games
If the proportion of the total disposable income spent on consumer goods and services is 93 percent and if
consumers spend 85 percent of each additional dollar, what is
a. the apc?
b. the aps?
c. the mpc?
d. the mps?
Answers
Answer:
what?????????????????
part b please, this is due tomarrow

Answers
The constant of variation is 62.5 and this means that the bus travel 62.5 miles per hour.
What is Proportional?Any relationship that is always in the same ratio and quantity which vary directly with each other is called the proportional.
We have to given that;
The given relation is,
⇒ y = 62.5x
Where, y represent distance in mile and x represent the time in hour.
We know that;
The proportional relation is defined as;
⇒ y = kx
Where, k is constant of variation.
Hence, By comparing,
The constant of variation is 62.5 and this means that the bus travel 62.5 miles per hour.
Learn more about the proportion visit:
https://brainly.com/question/1496357
#SPJ1
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
27
Lalculate the projected balance or casn at the end or August. A. \( \$ 23000 \) B. \( \$ 29000 \) C. \( \$ 107000 \) D. \( \$ 38000 \)
Answers
The projected balance of cash at the end of August is $38,000. The correct option is D.
To calculate the projected balance of cash at the end of August, we need to consider the cash balance at the beginning of the month, cash collections, and cash payments for August.
Given that the cash balance on July 31 was $32,000.00, we start with this amount.
Cash collections for August are $52,000.00, which means this amount is added to the cash balance.
Next, we consider cash payments for August, which include purchases of direct materials and operating expenses. The total cash payments for August are $20,000 (purchases of direct materials) + $26,000 (operating expenses) = $46,000.00. This amount is subtracted from the cash balance.
Finally, we calculate the projected balance of cash at the end of August by adding the cash collections and subtracting the cash payments from the beginning cash balance:
Projected cash balance at the end of August = Beginning cash balance + Cash collections - Cash payments
= $32,000 + $52,000 - $46,000
= $38,000
Therefore, correct option is D.
To learn more about balance click on,
https://brainly.com/question/32973850
#SPJ4
Complete question is:
Berman Company is preparing its budget for the third quarter. Cash balance on July 31 was $32,000.00. Assume there is no minimum balance of cash required and no borrowing is undertaken. Additional budgeted data are provided here:
July Aug Sep
Cash collections $51,000.00 $52,000.00 $50,000.00
Cash payments
Purchases of direct materials 23,000 20,000 24,000
Operating expenses 32,000 26,000 22,000
Capital expenditures 7,000 9,000 13,000
Calculate the projected balance of cash at the end of August.
A. $23000
B. $29000
C. $107000
OD. $38000
2. What is the probability of spinning an A on the first spinner and an odd number
on the second spinner? *

Answers
Answer:
1/10
Step-by-step explanation:
All spinners have equal areas & circumference on each outcome, so spinning an A is one out of five, or 1/5. The probability of spinning any number is 1/6. Since 1, 3, and 5 are all odd numbers, the probability of spinning an odd number is 3/6, or 1/2.
The probability of spinning both spinners successfully (an A AND an odd number) can be found by the product rule, which is the product of the two probabilities, namely 1/5 * 1/2 = 1/10.
andy can run 20 miles in 6 hours. how much miles can he run in 1 hour.
Answers
I see that this is a rate of change time of problem
If andy can run 20 miles in 6 hours, than our goal is to find out how much he runs in a hour
So, we just have to divide 20 by 6.
It's sorta hard to explain
Questions?
Anyhow, the answer is around 3.3 miles per hour
Answer:
3.33 miles
Step-by-step explanation:
We Know
Andy can run 20 miles in 6 hours.
How many miles can he run in 1 hour?
We Take
20 / 6 ≈ 3.33 miles
So, Andy can run about 3.33 miles in 1 hour.
OK so I need to know what 96÷6 is and I know it is 16 but I need to know how to do it in long division can anyone help me

Answers
Answer:
16
____________
6| 96
-6 |
V
36
- 36
0
6 goes into 9 one time because 9-6=3 so there is 1 six in 9. Write 1 at the top because you have 1 6.
Subtract the 6 and you get 3
Bring the 6 from 96 down
you get 36
6 goes into 36 6 times because 36-6-6-6-6-6-6=0 so write a 6 at the top and you get 16 because of the previous 1.
Subtract 36 by 36 to get 0
Hope this helps
Step-by-step explanation:
Answer:
16
Step-by-step explanation:
You have to take each number in the dividend (number being divided) and divide it by the number in the divisor (number that is dividing). Here you would take 9, the first number in the dividend and divide it by 6, and you would put that in the first space of the quotient (answer). You would then take that number and multiply it by 6 and place it in the space below. Subtract 6 from 9 and get 3. Drop down the 6 to get 36. Take 36 and divide that by the divisor 6 and get 6 next to the number 1 you calculated earlier to get your answer 16. Take 6 and multiply it back to get 36 and subtract it from 36 to get a remainder of 0.
I showed how to do it visually in the attachment just in case this explanation didn't make any sense
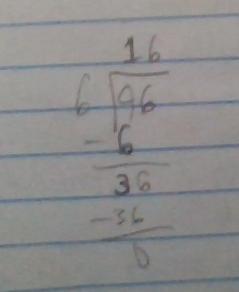
twice a number decreased by four is less than 8 is a equation or inequality
Answers
It is an inequality, and it can be written as:
2x- 4 < 8
Where x is the number.
Is this an equation or an inequality?Generally, if you see the words "less than, greater than, less or equal to, greater or equal to, etc.." you will be dealing with an inequality.
Here we have the mathematical statement:
"twice a number decreased by four is less than 8"
if we define x as the number, then we can write ""twice a number decreased by four..."
2x -4
And that must be less than 8, then we will have the inequality:
2x- 4 < 8
Learn more about inequalities at:
https://brainly.com/question/24372553
#SPJ1
Find the volume figure use 3.14 for pi the volume of the figure is about___ ___

Answers
The volume of the figure is approximately 1591.63 cm³.
We have,
To find the volume of the figure with a semicircle on top of a cone, we can break it down into two parts: the volume of the cone and the volume of the semicircle.
The volume of the Cone:
The formula for the volume of a cone is V = (1/3)πr²h, where r is the radius of the base and h is the height of the cone.
Given that the diameter of the cone is 14 cm, the radius (r) is half of the diameter, which is 7 cm.
The height (h) of the cone is 17 cm.
Plugging the values into the formula, we have:
V_cone = (1/3)π(7 cm)²(17 cm)
V_cone = (1/3)π(49 cm²)(17 cm)
V_cone = (1/3)π(833 cm³)
V_cone ≈ 872.67 cm³ (rounded to two decimal places)
The volume of the Semicircle:
The formula for the volume of a sphere is V = (2/3)πr³, where r is the radius of the sphere. In this case, since we have a semicircle, the radius is half of the diameter of the base.
Given that the diameter of the cone is 14 cm, the radius (r) of the semicircle is half of that, which is 7 cm.
Plugging the value into the formula, we have:
V_semicircle = (2/3)π(7 cm)³
V_semicircle = (2/3)π(343 cm³)
V_semicircle ≈ 718.96 cm³ (rounded to two decimal places)
Total Volume:
To find the total volume, we add the volume of the cone and the volume of the semicircle:
V_total = V_cone + V_semicircle
V_total ≈ 872.67 cm³ + 718.96 cm³
V_total ≈ 1591.63 cm³ (rounded to two decimal places)
Therefore,
The volume of the figure is approximately 1591.63 cm³.
Learn more about cones here:
https://brainly.com/question/13798146
#SPJ1
HELP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
When we simplify ∛6x⁸ and ∛7x⁷ by multiplying them, we will have ∛42(x⁵)
Simplification of VariablesSimplifying an algebraic expression, also called simplifying a variable expression, means writing the expression in the most basic way possible by eliminating parentheses and combining like terms
In the question given, the variables are ∛7x⁷ and ∛6x⁸, this can be;
When we simplify or find the product of ∛7x⁷ and ∛6x⁸, we will have
∛6x⁸ × ∛7x⁷ = ∛42(x⁵)
The is easily possible because we have both complex variables with the same root.
Learn more on simplification of variable here;
https://brainly.com/question/27894163
#SPJ1
12(Multiple Choice Worth 5 points)
(H2.03 MC)
Which of the following is NOT a key feature of the function h(x)?
(x - 5)²
-log₁ x +6
O The domain of h(x) is [0.).
O The x-intercept of h(x) is (5, 0)
h(x) =
0≤x≤4
X>4
O The y-intercept of h(x) is (0, 25).
O The end behavior of h(x) is as x→∞h(x)→∞

Answers
The feature NOT associated with the function h(x) is that the domain of h(x) is [0.).
The function h(x) is defined as (x - 5)² - log₁ x + 6.
Let's analyze each given option to determine which one is NOT a key feature of h(x).
Option 1 states that the domain of h(x) is [0, ∞).
However, the function h(x) contains a logarithm term, which is only defined for positive values of x.
Therefore, the domain of h(x) is actually (0, ∞).
This option is not a key feature of h(x).
Option 2 states that the x-intercept of h(x) is (5, 0).
To find the x-intercept, we set h(x) = 0 and solve for x. In this case, we have (x - 5)² - log₁ x + 6 = 0.
However, since the logarithm term is always positive, it can never equal zero.
Therefore, the function h(x) does not have an x-intercept at (5, 0).
This option is a key feature of h(x).
Option 3 states that the y-intercept of h(x) is (0, 25).
To find the y-intercept, we set x = 0 and evaluate h(x). Plugging in x = 0, we get (0 - 5)² - log₁ 0 + 6.
However, the logarithm of 0 is undefined, so the y-intercept of h(x) is not (0, 25).
This option is not a key feature of h(x).
Option 4 states that the end behavior of h(x) is as x approaches infinity, h(x) approaches infinity.
This is true because as x becomes larger, the square term (x - 5)² dominates, causing h(x) to approach positive infinity.
This option is a key feature of h(x).
In conclusion, the key feature of h(x) that is NOT mentioned in the given options is that the domain of h(x) is (0, ∞).
Therefore, the correct answer is:
O The domain of h(x) is (0, ∞).
For similar question on domain.
https://brainly.com/question/2264373
#SPJ8
Simplify 7(x + 3).
7x + 3
7x + 21
Ox+ 21
07x + 10
Answers
Answer:
The answer is 7x+21
Step-by-step explanation:
You just multiply 7 by both x and 3 but keep them separate
I WILL GIVE 20 POINTS TO THOSE WHO ANSWER THIS MATH QUESTION RIGHT NOOOO SCAMS PLEASE AND PLEASE EXPLAIN WHY THAT IS THE ANSWER. To the nearest whole number what is the area of the regular hexagon?
______units squared

Answers
Answer: 42
Step-by-step explanation:

What is the area of this figure ?? Please help

Answers
Answer: I would say 80 but I don't think that's right so sorry I don't really think I can help you with this question.
Step-by-step explanation:
Find the reciprocal of the numbers below: a. 1/3 b. 4/5 c. 7
Answers
Answer:
a. 1/3 = 3 b. 4/5 = 5/4 c. 7 = 1/7
Step-by-step explanation:
Reciprocal means switching the numerator to the denominator and the denominator to the numerator. Whenever you have a whole number, there is an imaginary 1 as the denominator that is why the reciprocal of 7 is 1/7.
Explain the difference between finding the vertex of a function written in vertex form and finding the vertex of a function written in standard form.
Answers
The equation in the vertex form will be y = (x + b/2a)² - b²/4a² + c/a and the equation in the standard form will be ax² + bx + c = 0.
What is a quadratic equation?The quadratic equation is given as ax² + bx + c = 0. Then the degree of the equation will be 2.
Convert the standard equation into a vertex form, then we have
x² + (b/a)x + (c/a) = 0
x² + (b/a)x + b²/4a² - b²/4a² + c/a = 0
(x + b/2a)² - b²/4a² + c/a = 0
Put h = - b/2a and k = - b²/4a² + c/a, where (h, k) be the vertex of the parabola. Then the equation will be
(x - h)² + k = 0
The function written in vertex form will be y = (x - h)² + k and in the standard form will be ax² + bx + c = 0.
More about the quadratic equation link is given below.
https://brainly.com/question/2263981
#SPJ1
Find the center and the radius and the center of the circle with the given equations:

Answers
Answer:
3. (-1 , 3) , 4
4. (0 , -7), 8
Step-by-step explanation:
circle: (x-h)² + (y-k)² = r²
3. x²+2x+y²-6y-6 =0
(x²+2x+1) + (y²-6y+9) -16 =0
(x+1)² + (y-3)² = 4²
center(-1 , 3) radius: 4
4. x²+y²+14y-15=0
(x+0)² + (y²+14y+7²) - 64 = 0
(x+0)² + (y+7)² = 8²
center: (0 , -7) radius: 8
Answer:
3. Center = (-1,3) Radius = 4
4. Center = (0,-7) Radius = 8
use completion of squares to find the solution, if you do not understand what this means, there is a great video on utube by the channel Prep Expert that explains finding the center of a circle based on an equation.
A ball is rolling along the x-axis. Its position in feet) at time x (n seconds) is given by f (x)=2Vx. Find its instanta- neous rate of change when x +9 seconds. Select one: a. 6 ft/sec b. 1/12 ft/sec c. 1/3 ft/sec d. 2/3fty sec
Answers
The concept of instantaneous rate of change, also known as derivative, gives us the rate at which a quantity changes with respect to time at a specific instant. To find the instantaneous rate of change, we can take the derivative of the function that describes the position of the ball.
In this case, the position of the ball is given by the function f(x) = 2Vx, where V is the initial velocity of the ball. Taking the derivative of the function, we get the derivative as f'(x) = 2V, which represents the instantaneous rate of change of the ball's position with respect to time at any instant x.
When x = 9 seconds, the instantaneous rate of change of the ball's position is given by f'(9) = 2V. Therefore, the correct answer is d. 2/3V ft/sec.
Here you can learn more about concept of instantaneous rate of change
https://brainly.com/question/15341089#
#SPJ11
plezzzz help me answer this question it will mean a lot

Answers
Answer:
1A: 5
1B: y = 3x + 10
Step-by-step explanation:
standard form is y = mx + b
M is your slope, B is your intercept
parallel lines have the same slope with different intercepts
Solve the proportion

Answers
just put the y on the side and the numbers on the other side and that’s it
What is the equation of the line that passes through the points (-2, 4) and (0,10)?
Answers
Answer:
y = 3x + 10
Step-by-step explanation:
first use slope formula:
\(\frac{4-10}{-2-0}\) = \(\frac{-6}{-2}\) = 3
then plug that and the y-intercept into y = mx + b
Answer:
y = 3x+10
Step-by-step explanation:
hope this helps
Donna took twice as long to drive 720 miles and Maple took to drive 200 miles. Find the rates and ties of both if Donna's speed exceeded that of Maple by 40 miles per hour
Answers
Answer:
Donna traveled for 8 hours at 90 mph
Maple traveled for 4 hours at 50 mph
Step-by-step explanation:
The velocity at which each person traveled is given by the distance traveled divided by the time spent (t). From the information given, the following expressions can be written
\(t_d = 2t_m\\V_d = V_m+40\\V_d = \frac{720}{t_d}\\V_m = \frac{200}{t_m}\\\\V_d = \frac{360}{t_m}\\ \frac{360}{t_m}=\frac{200}{t_m}+40\\t_m = 4\ hours\\t_d=2*4 = 8\ hours\\\\V_d = \frac{720}{8}=90\ mph\\V_m = \frac{200}{4}=50\ mph\\\)
Therefore, Donna traveled for 8 hours at 90 mph and Maple traveled for 4 hours at 50 mph.
Match the slopes and lengths of the side of polygon A’B’C’D’ to their values

Answers
In the given polygon we have: Slope of A'B' = 5, Length of A'D' = 8.4, Length of C'D' = 5.4, Slope of B'C' = 0.25.
What is dilation?Resizing an item uses a transition called dilation. Dilation is used to enlarge or contract the items. The result of this transformation is an image with the same shape as the original. However, there is a variation in the shape's size. The initial shape should be stretched or contracted during a dilatation. The phrase "scale factor" describes this transition.
Enlargement is the term used when a dilatation results in a larger image.
Reduction occurs when a dilatation results in a smaller picture.
When the polygon ABCD is dilate by 1.2 units the slope of the segments of the polygon remains the same, whereas the length of the segments are multiplied by 1.2 units.
Thus.
Slope of A'B' = 5
Length of A'D' = 8.4
Length of C'D' = 5.4
Slope of B'C' = 0.25
Hence, in the given polygon we have: Slope of A'B' = 5, Length of A'D' = 8.4, Length of C'D' = 5.4, Slope of B'C' = 0.25.
Learn more about dilation here:
https://brainly.com/question/13176891
#SPJ1
HELP PLEASE SOLVE ITS SLOPE!

Answers
Step-by-step explanation:
1. gradient=y2-y1/x2-x1
=21-9/-7-(-12)
=21-9/-7+12
=12/5
2.consider any two coordinates:
(13,32),(7,33)
gradient:
=33-32/7-13
=1/-5