The measures of the angles of a triangle are shown in the figure below. Solve for x.

Answers
Answer and Step-by-step explanation:
All triangles have a sum of their angles to be 180 degrees. So, to find x, we need to subtract the two given sides from 180 degrees.
180 - 38 - 83 = 59
x = 59 degrees.
#teamtrees #PAW (Plant And Water)
Step by step explanation:
Related Questions
A child rolls a ball on a level floor 3.5m to another child. If the ball makes 15.0 revolutions, what is its diameter?
Answers
The diameter of the ball is approximately 16.67 meters.
To find the diameter of the ball, we can use the relationship between the distance traveled and the number of revolutions.
The circumference of a circle is given by the formula C = πd, where C is the circumference and d is the diameter.
Given that the ball rolls a distance of 3.5 meters and makes 15.0 revolutions, we can calculate the circumference of the path it travels:
C = 3.5 m * 15.0 = 52.5 m
Since each revolution covers the circumference of the ball, we have C = πd. Plugging in the known value for C, we can solve for the diameter (d):
52.5 m = πd
Dividing both sides of the equation by π, we get:
d = 52.5 m / π
Using a calculator, we can evaluate this expression:
d ≈ 16.67 meters
Learn more about circles and circumferences here:
https://brainly.com/question/17130827
#SPJ11
move 3 units and 1 units from the origin
Answers
Answer:
It depends on which why you are moving so let's say you have to move the 3 units to the right and 1 up, that would be the answer. I can't really give you the exact answer because you didn't say where they are supposed to go.
suppose the random variables x, y, z and have joint pdf as follows: f(x, y, z)= xy²z/180, x = 1, 2, 3; y = 1, 2, 3
find the marginal pdf of f₁,₃(2,3). (Round off to third decimal place) of x and z.
Answers
The marginal pdf of f₁,₃(2,3) of x and z is approximately 0.096.
To find the marginal pdf of f₁,₃(2,3) of x and z, we need to integrate the joint pdf over the range of y while fixing x = 2 and z = 3.
The marginal pdf of x and z, denoted as f₁,₃(x,z), is given by:
f₁,₃(x,z) = ∫ f(x, y, z) dy
Plugging in x = 2 and z = 3 into the joint pdf, we have:
\(f(2, y, 3) = (2y^2)/180\)
Now we integrate f(2, y, 3) with respect to y from 1 to 3:
\(f_1,_3(2, 3) = \int[(2y^2)/180]\) dy from 1 to 3
Evaluating the integral, we get:
\(f_1,_3(2, 3) = (2/180) \int y^2 dy\) from 1 to 3
\(= (2/180) [(y^3/3)]\) from 1 to 3
\(= (2/180) [(3^3/3) - (1^3/3)]\)
= (2/180) [27/3 - 1/3]
= (2/180) [26/3]
= 52/540
≈ 0.096
Therefore, the marginal pdf of f₁,₃(2,3) of x and z is approximately 0.096.
A marginal pdf is what?
A probability density function (pdf) may be used to characterise the univariate distribution of each element in the random vector. To distinguish it from the joint probability density function, which shows the multivariate distribution of each entry in the random vector, this is known as the marginal probability density function.
To learn more about marginal pdf from the given link
https://brainly.com/question/31746000
#SPJ4
Sketch the region whose area is given by the integral and evaluate the integral---
/int from pi/4 to 3pi/4 /int from 1 to 2 r dr d(theta)
Answers
The integral /int from pi/4 to 3pi/4 /int from 1 to 2 r dr d(theta) represents the double integral of a region in polar coordinates.
The region can be visualized as a sector of a circle in the polar plane, bounded by the angles pi/4 and 3pi/4, and by the radii 1 and 2. The first integral /int from 1 to 2 r dr integrates over the radial direction, while the second integral /int from pi/4 to 3pi/4 d(theta) integrates over the angular direction.
To evaluate the integral, we integrate the radial part first. Integrating r with respect to r yields (1/2)r^2. Plugging in the limits of integration, we get [(1/2)(2)^2] - [(1/2)(1)^2] = 2 - 1/2 = 3/2.
Next, we integrate the angular part. Integrating d(theta) with respect to theta gives theta. Evaluating the limits of integration, we have (3pi/4) - (pi/4) = pi/2.
Finally, multiplying the results of the radial and angular integrals, we have the value of the double integral as (3/2) * (pi/2) = 3pi/4. Thus, the integral evaluates to 3pi/4.
Learn more about polar coordinates here: brainly.com/question/31904915
#SPJ11
let f(t)f(t) be the number of us billionaires in year tt. in 1985 there were 13 us billionaires, and in 1990 there were 99 us billionaires. assuming the yearly increase remains constant, find a formula predicting the number of us billionaires in year tt.
Answers
The formula predicting the number of US billionaires in any given year (t) is:f(t) = 17.2t - 34,129. We can assume a linear growth model on the based of given information.
The given data states that in the year 1985, there were 13 US billionaires. Whereas in 1990, there were 99 US billionaires. We have to find out the formula that predicts the number of US billionaires in any given year (t).
The yearly increase remains constant, so we can consider the formula for the linear function.f(t) = mt + b
where
t is the year and f(t) is the number of US billionaires in that year (t).
m is the slope of the line and b is the y-intercept.
The slope of the line is given by the formula:m = (y₂ - y₁) / (x₂ - x₁)
Let's plug in the given values to find the slope of the line.m = (99 - 13) / (1990 - 1985)m = 86 / 5m = 17.2 .The y-intercept of the line can be found by substituting the values of t and f(t) from any of the given points into the equation of the line.
Let's use the point (1985, 13).f(t) = mt + b => f(1985) =17.2(1985) + b => f(1985) = 34,142 + b =>b = 13 - 34,142 & b = -34,129.
The formula predicting the number of US billionaires in any given year (t) is:f(t) = 17.2t - 34,129
To know more about linear growth model refer here:
https://brainly.com/question/28033207
#SPJ11
Differentiate implicitly to find dy/dx. sec(xy) + tan(xy) + 7 = 25 dy dx əz х 11 Differentiate implicitly to find the first partial derivatives of z. x In(y) + y²z+ z² = 53 əz ду Find the derivative of the function. y = cos(a5 + x5)
Answers
The derivative of the function \(y = cos(a^5 + x^5)\) is \(-5x^4 * sin(a^5 + x^5).\)To differentiate implicitly, we'll use the chain rule and the product rule as necessary.
Let's go through each problem step by step:
1. Differentiate implicitly to find dy/dx in the equation sec(xy) + tan(xy) + 7 = 25 dy/dx.
To differentiate implicitly, we treat y as a function of x and apply the chain rule. Let's differentiate each term:
d/dx(sec(xy)) = sec(xy) * (y * d/dx(xy)) = sec(xy) * (y * (d/dx(x) * y + x * d/dx(y))) = sec(xy) * (y * (1 * y + x * dy/dx))
d/dx(tan(xy)) = tan(xy) * (y * d/dx(xy)) = tan(xy) * (y * (d/dx(x) * y + x * d/dx(y))) = tan(xy) * (y * (1 * y + x * dy/dx))
The equation becomes:
sec(xy) * (y * (1 * y + x * dy/dx)) + tan(xy) * (y * (1 * y + x * dy/dx)) + 7 = 25 * dy/dx
Now, let's solve for dy/dx:
\(sec(xy) * y^2 + tan(xy) * y^2 + 7 = 25 * dy/dxsec(xy) * y^2 + tan(xy) * y^2 - 25 * dy/dx = -7dy/dx = (sec(xy) * y^2 + tan(xy) * y^2 + 7) / -25\)
2. Differentiate implicitly to find the first partial derivatives of z in the equation\(x * ln(y) + y^2z + z^2 = 53.\)
To differentiate implicitly, we'll differentiate each term with respect to x and y and solve for the partial derivatives. Let's go step by step:
Differentiating with respect to x:
d/dx(x * ln(y)) = ln(y) * d/dx(x) + x * d/dx(ln(y)) = ln(y) + x * (1/y) * dy/dx
Differentiating with respect to y:
d/dy(x * ln(y)) = x * d/dy(ln(y)) = x * (1/y) * dy/dy = x/y
\(d/dy(y^2z) = 2yz * dy/dy + y^2 * d/dy(z) = 2yz + y^2 * dz/dy\\d/dy(z^2) = 2z * dz/dy\)
The equation becomes:
\(ln(y) + x * (1/y) * dy/dx + x/y + 2yz + y^2 * dz/dy + 2z * dz/dy = 0\)
Rearranging terms, we can solve for the partial derivatives:
\(dy/dx = -ln(y) * y / (x + y^2) \\dz/dy = -(ln(y) + x/y + 2yz) / (2z + y^2)\)
3. Find the derivative of the function \(y = cos(a^5 + x^5).\)
To find the derivative, we'll use the chain rule. Let's differentiate step by step:
\(d/dx(cos(a^5 + x^5)) = -sin(a^5 + x^5) * (d/dx(a^5 + x^5))\)
\(d/dx(a^5 + x^5) = 0 + 5x^4 = 5x^4\)
The equation becomes:
\(d/dx(cos\)\((a^5 + x^5)) = -sin(a^5 + x^5) * 5x^4\)
Therefore, the derivative of\(y = cos(a^5 + x^5) is -5x^4 * sin(a^5 + x^5).\)
Learn more about differentiate here: https://brainly.com/question/24062595
#SPJ11
measured the sides of a right triangle to be 15cm and 8cm. Find the length of the hypotenuse.
Answers
c = √225 + 64
c = √289
c = 17
The lenght of the hypotenuse is 17.
PLEASE HELP! I WILL MAKE YOU BRAINLIST!

Answers
Answer: I think it is C
Step-by-step explanation: 32/4=8 so 1 cm = 8km
Choose the expression that is equivalent to a fraction with nine raised to the negative third power in the numerator and the quantity three raised to the negative second power times nine squared end quantity in the denominator and the entire fraction is cubed.
Answers
The expression that is equivalent to a fraction with nine raised to the negative third power in the numerator and the quantity three raised to the negative second power times nine squared end quantity in the denominator and the entire fraction is cubed is \(\frac{3^{6} }{9^{15} }\)
Nine raised to the negative third power = \(9^{-3}\)
Three raised to the negative second power times nine squared = \((3x^{-2})(9^{2} )\)
The expression is \((\frac{9^{-3} }{(3^{-2})(9^{2} ) } )^{3}\)
=\(\frac{9^{(-3)(3)} }{(3^{(-2)(3)})(9^{(2)(3)} }\)
=\(\frac{9^{-9} }{(3^{-6})(9^{6}) }\)
= \(\frac{3^{6} }{(9^{9})(9^{6}) }\)
= \(\frac{3^{6} }{9^{15} }\)
Hence, the expression that is equivalent to a fraction with nine raised to the negative third power in the numerator and the quantity three raised to the negative second power times nine squared end quantity in the denominator and the entire fraction is cubed is \(\frac{3^{6} }{9^{15} }\)
Learn more about expression here
brainly.com/question/14083225
#SPJ1
what’s the answer
r+11+ Br= 29
Answers
r= 18/1+b
B= -1 + 18/r
HELP !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
\(-2.3 > -\frac{8}{3}\)
Step-by-step explanation:
-2.3 = -2.3333333333...
-8/3 = -2.666666666...
You can see that -2.6 is less than -2.3
Answer: B
Step-by-step explanation:
A bar over a number means the number is irrational, and the number will repeat. so the numbers are -2.33333333333 and -8/3.
If 8/3 = 2.6666667, then -8/3 will be -2.6666667.
-2.6666666667 is lower than -2.33333333. So the equation is -2.3333333333 > - 8/3.
Ron has 8 boxes of milk chocolate. Each box has the same number of chocolates. Jake has 12 boxes of dark chocolate. Each box has the same number of chocolates.
If m represents the number of milk chocolates and d represents the number of dark chocolates in each box, determine which of the following expressions show the total number of chocolates.
Answers
Answer:
8m+12d=?
Step-by-step explanation:
Can someone please help me ASAP?? It’s due today!! I will give brainliest If It’s all correct.
Please do part a, b, and c

Answers
B when cut perpendicular it’s a square.
C we know it is a 12 meter by 3 meter rectangle because we cut it.
For the function f(x) = x2
Find f(5) =
Find f(-5) =
Answers
\(f(x)= (x)^{2}\)
=> f(5) = (5)^2 = 25
=> f(-5) = (-5)^2 = 25
Answer:
25
Step-by-step explanation:
..............
Big Red, Inc. rents trucks on a weekly basis. Trucks are picked up and dropped off at one of 5 locations: • Enid, Oklahoma • Topeka, Kansas Broken Bow, Nebraska • Goodland, Kansas Amarillo, Texas Management has developed the following "transition matrix". This matrix gives the probability of a truck being returned at each of the locations given the city where it was picked up: .05 .2 2 Return City Enid | Topeka Broken Bow | Goodland Amarillo Enid .3 .35 2 Topeka .25 .15 Broken Bow .05 .1 Goodland 4 .05 .1 .15 .3 Amarillo 35 .4 .1 .05 For example, if a truck is picked up in Goodland, there is a 30% chance that it will be returned in Amarillo. Pick Up City .35 1 a. Beginnings with a truck in Broken Bow, Nebraska, simulate the rental and location of a truck for a 20-week period. Start by developing a discrete random variable generator for each city. Use the random numbers given in the table below. Week Return City Pickup City Broken Bow r 0.45 0.69 0.33 0.69 0.88 0.16 0.7 10 11 12 13 14 0.7 0.07 0.37 0.03 0.47 0.06 0.55 0.86 0.25 0.63 0.18 0.63 0.18 15 16 17 18 19 20 b. From the simulation experiment, determine the percentage of time a truck will be returned in each city. Number of Returns % Returned City Enid Topeka Broken Bow Goodland Amarillo Total 20 T C. Discuss how this simulation might be changed to yield more accurate results.
Answers
Answer:
To yield more accurate results, we could increase the number of simulation runs, use more random numbers, or use a more sophisticated simulation method such as Monte Carlo simulation.
Step-by-step explanation:
a. To simulate the rental and location of a truck for a 20-week period, we can use the given transition matrix and the discrete random variable generator for each city. Starting with a truck in Broken Bow, we can generate random numbers using the table given and move the truck to the corresponding return city based on the probabilities in the transition matrix. The results of the simulation experiment are shown in the table below.
Week Return City Pickup City
Broken Bow r
1 Goodland Goodland
2 Goodland Goodland
3 Goodland Broken Bow
4 Amarillo Goodland
5 Amarillo Amarillo
6 Goodland Enid
7 Amarillo Goodland
8 Goodland Goodland
9 Goodland Topeka
10 Amarillo Goodland
11 Goodland Enid
12 Goodland Goodland
13 Amarillo Goodland
14 Goodland Goodland
15 Goodland Goodland
16 Goodland Enid
17 Topeka Goodland
18 Amarillo Goodland
19 Goodland Goodland
20 Goodland Goodland
b. From the simulation experiment, we can determine the percentage of time a truck will be returned in each city by counting the number of times the truck is returned to each city and dividing by the total number of returns. The results are shown in the table below.
Number of Returns % Returned City
Enid 0 0%
Topeka 1 5%
Broken Bow 15 75%
Goodland 3 15%
Amarillo 1 5%
Total 20 100%
c. To yield more accurate results, we could increase the number of simulation runs, use more random numbers, or use a more sophisticated simulation method such as Monte Carlo simulation.
Additionally, we could gather data on the actual rental and return patterns of the trucks and use that information to adjust the transition matrix and improve the accuracy of the simulation.
To know more about Monte Carlo simulation, refer here:
https://brainly.com/question/15350591
#SPJ11
y+4=3(x-3) rewrite in Ax+By=C
Answers
Answer:
0=3x-y=-13
Step-by-step explanation:
Answer:
In the equation y+4=3(x-3), we can see that x and y are the variables and 4 and -3 are the constants.
To convert the equation to the form Ax + By = C, we'll first distribute the 3 on the right side:
y + 4 = 3x - 9
Next, we'll move all the terms with x to one side of the equation and all the terms with y to the other side:
-3x + y = - 13
Now we have the equation in the form Ax + By = C, where A = -3, B = 1, and C = -13.
Insert < >, or= to make the following sentence true.

Answers
Answer:
it would be “>”, 100% guaranteed.
Answer:
answer is >
Step-by-step explanation:
hope this is helpful
A circle in the xy-plane has a diameter with endpoints (2,4) and (2,14). An equation of this circle is (x-2)^2+(y-9)^2=r^2 ,where r is a positive constant. What is the value of r?
Answers
So we see that r = 0. Therefore, the equation of the circle is just:
(x - 2)^2 + (y - 9)^2 = 0
Company revenue quadratic function.
Angel
The revenue, in billions of dollars, for a company in the year 2002 was $2.7 billion. One year later, in 2003, the revenue had risen to $3.4 billion. In 2005, the revenue climbed to $3.9 billion, before falling to $2.7 billion in 2008. The revenue, r, in billions of dollars, for the company, is a quadratic function of the number of years since 2002, x. what is the vertex of the function?
To find the quadratic function that represents the revenue of the company as a function of the number of years since 2002, we can use the vertex form of a quadratic function:
r(x) = a(x - h)^2 + k
where a is the coefficient of the quadratic term, h is the x-coordinate of the vertex, and k is the y-coordinate of the vertex.
We can use the given revenue values to set up a system of three equations:
2.7 = a(0 - h)^2 + k
3.4 = a(1 - h)^2 + k
2.7 = a(6 - h)^2 + k
Subtracting the first equation from the second, and the first equation from the third, we get:
0.7 = a(1 - h)^2
0 = a(6 - h)^2
Since a cannot be zero (otherwise we wouldn't have a quadratic function), we can divide the second equation by the first to get:
6 - h = 10
which gives us h = -4.
Substituting h = -4 into the first equation, we get:
2.7 = a(0 - (-4))^2 + k
2.7 = 16a + k
Substituting the revenue value for 2005, we get:
3.9 = a(3 - (-4))^2 + k
3.9 = 49a + k
Solving for a and k, we get:
a = -0.1
k = 4.3
Therefore, the quadratic function that represents the revenue of the company as a function of the number of years since 2002 is:
r(x) = -0.1(x + 4)^2 + 4.3
The vertex of this function is at (-4, 4.3).
Angel
What is the sum of the numbers in the sequence 3, −4, 5, −6, . . . , 101?
We can notice that the sequence alternates between adding an odd number and subtracting an even number. The first term is 3, which is odd, so the sequence starts by adding an odd number. The second term is -4, which is even, so the sequence then subtracts an even number. This pattern continues, so the sum of the sequence can be written as:
3 - 4 + 5 - 6 + ... + 101
We can group the terms into pairs:
(3 - 4) + (5 - 6) + ... + (99 - 100) + 101
Each pair of terms adds up to -1, so we can simplify the expression to:
-1 -1 -1 ... -1 + 101
where there are 50 pairs of -1's. The sum of 50 -1's is -50, so the sum of the sequence is:
-50 + 101 = 51
Therefore, the sum of the numbers in the sequence 3, −4, 5, −6, . . . , 101 is 51.
Angel
What is 12 7/8 - 56/17?
To subtract mixed numbers like 12 7/8, we first need to convert it to an improper fraction. We can do this by multiplying the whole number by the denominator of the fraction, and adding the result to the numerator. This gives us:
12 7/8 = (12 × 8 + 7)/8 = 103/8
Now we can subtract 56/17 from 103/8. To do this, we need to find a common denominator for the two fractions. The least common multiple of 8 and 17 is 136, so we can rewrite the fractions with this denominator:
103/8 = (103/8) × (17/17) = 1751/136
56/17 = (56/17) × (8/8) = 448/136
Now we can subtract the two fractions:
1751/136 - 448/136 = (1751 - 448)/136 = 1303/136
We can simplify this fraction by finding a common factor to divide both the numerator and denominator. Since both 1303 and 136 are relatively prime, we cannot simplify it any further. Therefore, the final answer is:
12 7/8 - 56/17 = 1303/136
Angel
A circle in the xy-plane has a diameter with endpoints (2,4) and (2,14). An equation of this circle is (x-2)^2+(y-9)^2=r^2 ,where r is a positive constant. What is the value of r?
The center of the circle is the midpoint of the diameter, which is at (2, (4+14)/2) = (2, 9). We can substitute this center point into the equation of the circle to get:
(x - 2)^2 + (y - 9)^2 = r^2
(2 - 2)^2 + (9 - 9)^2 = r^2
0 + 0 = r^2
So we see that r = 0. Therefore, the equation of the circle is just:
(x - 2)^2 + (y - 9)^2 = 0
This describes a single point in the xy-plane, which is the center of the circle. Note that this point is already on the given diameter, so it makes sense that the radius is zero.
What is the square root of r^64
Answers
Answer:
the answer is 8
Step-by-step explanation:
because the (8)²is 8×8is 64
Mrs. Fisher is remodeling her house and needs to buy wallpaper border for her living room. She used her tape measure and found that the wall is 197 inches wide. When she arrived at the store she discovered that the border is only sold in yard-long increments. How many yards of border should Mrs. Fisher purchase ? How many yards of border does Mrs. Fisher actually need? Round your answer to the nearest thousandth.
Answers
Answer:23.7
Step-by-step explanation:
A store sells a television for $1000. There are two payment options. Which option is better? ( PLS HELP!! I'M RLY STRUGGLING!! :< )

Answers
A coordinate plane is labeled street on the x-axis and avenue on the y-axis. ping is at point (3, 6) and ari is at point (21, 18). a line is drawn from ping to ari. ping lives at the corner of 3rd street and 6th avenue. ari lives at the corner of 21st street and 18th avenue. there is a gym two-thirds the distance from ping's home to ari's home. x = (startfraction m over m n endfraction) (x 2 minus x 1) x 1 y = (startfraction m over m n endfraction) (y 2 minus y 1) y 1 where is the gym? 9th street and 10th avenue 12th street and 12th avenue 14th street and 12th avenue 15th street and 14th avenue
Answers
The gym location is (15th street, 14th Avenue). so the option D is correct.
What is graph ?A graph contains data of which input maps to which output.
Analysis of this leads to the relations which were used to make it.
Given :
Ping's residence = (3rd street, 6th Avenue)
Ari's residence = (21st street, 18th Avenue)
Gym location is 2/3 the distance of Ping's residence to Ari's residence
So, distance between Ping's home to Ari's home will be
Distance = (21st street, 18th Avenue) - (3rd street, 6th Avenue)
Distance = (21 - 3) street, (18 - 6) avenue
Distance between ping and Ari will be
= (18th , 12th )
We know that
Gym distance = 2/3 × (18), 2/3 ×(12)
Gym distance = (12, 8)
Gym location = Ping's location + gym distance
Gym location = (3rd street, 6th Avenue) + (12th street, 8th Avenue)
Gym location = (15th street, 14th Avenue)
Learn more about finding the graphed function here:
https://brainly.com/question/27330212
#SPJ1

Please can someone help!

Answers
Answer:
Charles: 17 points
Adam: 25 points
Bethany: 30 points

Answer:
Adam scored 25 points.
Bethany scored 30 points.
Charles scored 17 points.
Step-by-step explanation:
A = Adam, B = Bethany, C = Charles
What we know:
C + 8 = A
A + 5 = B
A + B + C = 72
Charles:
C + 8 + 5 = B
C + (C + 8) + (C + 13) = 72
72 - 8 - 13 = 51
51/3 = 17
Charles scored 17 points.
Bethany:
17 + 13 = 30
Bethany scored 30 points.
Adam:
17 + 8 = 25
Adam scored 25 points.
please write the question number and then answer the question plzz





Answers
PLS HELP THIS IS HARD ANYONE PLS
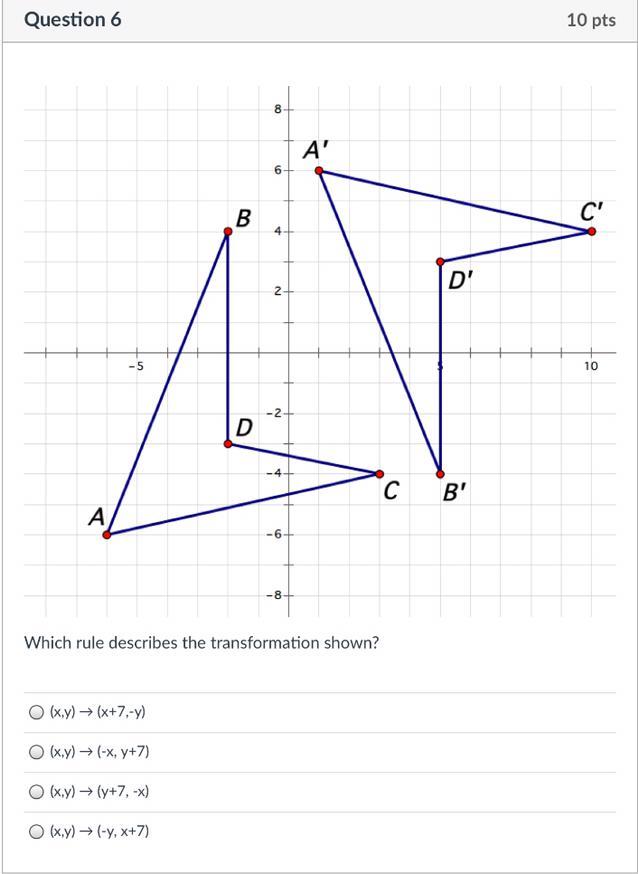
Answers
Answer:
it's going to be the first one, (x+7,-y)
Step-by-step explanation:
take one point, A for example and count how far it moved left and right. left is negative, right is positive, do the same for y
1. (5 points) rewrite the integral z 1 0 z 3−3x 0 z 9−y 2 0 f(x, y, z) dzdydx in the order of dx dy dz.
Answers
Given integral is z 1 0 z 3−3x 0 z 9−y 2 0 f(x, y, z) dzdydx.We have to rewrite this integral in the order of dx dy dz.So, by finding the limits for x, y, and z, we can rewrite the given integral in the order of dx dy dz as ∫(from 0 to 9)∫(from 0 to √(9-y²))∫(from 0 to 3-((1/3)*x))f(x,y,z)dzdydx.
We have given, z 1 0 z 3−3x 0 z 9−y 2 0 f(x, y, z) dzdydxWe have to rewrite this integral in the order of dx dy dz.So, we can solve this problem using the below steps :
Step 1: First of all, find out the limits for x, y and z and write them accordingly for x, y and z in the order of dx dy dz.
Step 2: Rewrite the given integral in the order of dx dy dz.
Step 3: Solve the above integral by using the limits for x, y and z.
Using the above steps, we can solve this problem.
Given integral is z 1 0 z 3−3x 0 z 9−y 2 0 f(x, y, z) dzdydx. Let's rewrite this integral in the order of dx dy dz by finding the limits of x, y, and z in the given integral.
So, z 1 0 z 3−3x 0 z 9−y 2 0 f(x, y, z) dzdydx = ∫(from 0 to 9)∫(from 0 to √(9-y²))∫(from 0 to 3-((1/3)*x))f(x,y,z)dzdydx
Summary:Given integral is z 1 0 z 3−3x 0 z 9−y 2 0 f(x, y, z) dzdydx.We have to rewrite this integral in the order of dx dy dz.So, by finding the limits for x, y, and z, we can rewrite the given integral in the order of dx dy dz as ∫(from 0 to 9)∫(from 0 to √(9-y²))∫(from 0 to 3-((1/3)*x))f(x,y,z)dzdydx.
Learn more about integral click here:
https://brainly.com/question/3009
#SPJ11
Special right triangles please help!
Find the variable

Answers
Answer:
11. s = 14
12. k = 24
Step-by-step explanation:
There are two "special" right triangles that show up in trig and geometry problems.
The isosceles right triangle has angles of 45°-45°-90°, and side length ratios 1 : 1 : √2.
The half-equilateral triangle has angles of 30°-60°-90°, and side length ratios 1 : √3 : 2.
You will do yourself a favor if you remember and learn to recognize these triangles.
__
11.)The hypotenuse of the isosceles right triangle is 14√2. This tells you the basic ratio has been multiplied by 14. The side length is ...
s = 14
__
12.)The half-equilateral triangle has middle-length side 12√3. This means the basic ratio has been multiplied by 12. The triangle short side is 12, and the long side is twice that:
k = 24
Women I
Men
Grocery Options
Store Online Total
Total
14
6
27
62
Answers
Given:
A survey stopped men and women at random to ask them where they purchased groceries, at a local grocery store or online. Grocery Options
Store Online Total
Women 23 12 35
Men 22 15 37
Total 45 27 72
Required:
To find the percentage of the people surveyed shop at a local grocery store.
Explanation:
The total number of people is 75.
And the total number of people surveyed shop at a local grocery store is 45.
Now the percentage of the people surveyed shop at a local grocery store is,
Final Answer:
63% of the people surveyed shop at a local grocery store.
If $\frac{9u-11}{2} = \frac{19u+11}{3}$, what is the value of $u$?
Answers
Solving the Question
We're given:
\($\frac{9u-11}{2} = \frac{19u+11}{3}\)
⇒ First, let's get rid of the fractions by multiplying both sides by 2 and 3:
\(\dfrac{9u-11}{2}*2 = \dfrac{19u+11}{3}*2\\\\9u-11= \dfrac{2(19u+11)}{3}\\\\3(9u-11)= \dfrac{2(19u+11)}{3}*3\\\\3(9u-11)= 2(19u+11)\)
⇒ Expand the parentheses:
\(27u-33= 38u+22\)
⇒ Isolate u:
\(27u-38u= 22+33\\-11u= 55\\u=-5\)
Answeru = -5
How many significant figures does 00.4463 have?