Answers
Answer:
A goes to K. C goes to M. B goes to L.
Step-by-step explanation:
:)
Related Questions
What is the value of x? Enter your answer in the box.
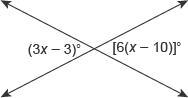
Answers
Answer:
19
Step-by-step explanation:
Since these two are vertical angles, their measure must be equal. Therefore:
\(3x-3=6(x-10) \\\\3x-3=6x-60 \\\\3x+57=6x \\\\3x=57 \\\\x=19^{\circ}\)
Hope this helps!
Answer:
19
Step-by-step explanation:
The two angles are vertically opposite angles, so they are equal.
3x - 3 = 6 (x - 10)
3x - 3 = 6x - 60
3x - 6x = - 60 + 3
-3x = -57
x = -57/-3
x = 19
8 1/5 + 1 2/3
NEED HELP
Answers
Answer: 9.7
Step-by-step explanation: add up the mixed numbers
3x+y = 18 x= -2y + 1 Solve by substitution
Answers
Answer:
Step-by-step explanation:
3x+y = 18 x= -2y + 1 Solve by substitution
Answer:
i think its 4.9 or 6.8
Step-by-step explanation:
Question 3 The Schwarzschild metric is given by 2M 2M ds² -(₁-²M) di² + (1-²¹)- 1- dr² +r² (d0² + sin² 0 dó²). There are Killing vectors associated with time invariance and angular momen- tum invariance in the direction in this geometry leading to the conserved quantities e = (1-2) and l= r² sin² 0 dr From this one can derive an analog to the radial energy equation in Newtonian mechanics by orienting the coordinates so that the orbits are confined to the equatorial plane where 0 = π/2 and u = 0. One finds 2 1 dr + Veff (r) = E 2 dr (e²_ -1) where E = and Veft(r) = - + 2/²/²2 - Mp³². Further, for circular orbits one can show that M | [₁ + √/₁−12 (+1)]. r+= | 2M Finally, for circular orbits of radius R do 1/2 M dt R³ (a) Which value of r corresponds to the Schwarzschild radius of stable circular orbits: r or r? Justify your answer. [3 marks] (b) Show that for circular orbits of radius R do 1/2 M -1/2 3M (²) ¹² (1-³) dT R³ R where is the proper time. [6 marks] (c) A free particle is moving in a circular orbit around a spherical source of curvature of mass M. The Schwarzschild radius of the orbit is 8M. Use the equivalence principle to argue that the period as measured at infinity should be larger than that measured by the particle. [4 marks] (d) Find the period of the orbit as measured by an observer at infinity. Find the period of the orbit as measured by the particle. [7 marks] M
Answers
(A) Circular orbits of stable particles are possible at radii greater than three times the Schwarzschild radius for the non-rotating spherically symmetric mass.
This represents the radius of a black hole's event horizon, within which nothing can escape. The Schwarzschild radius is the event horizon radius of a black hole with mass M.
M can be calculated using the formula: r+ = 2Mwhere r+ is the radius of the event horizon.
(B) 1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ R. This is the required expression.
Tau is the proper time of the particle moving around a circular orbit. Hence, by making use of the formula given above:1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ dt.
(C) Time passes differently in different gravitational fields, and it follows that the period as measured at infinity should be larger than that measured by the particle.
The principle of equivalence can be defined as the connection between gravitational forces and the forces we observe in non-inertial frames of reference. It's basically the idea that an accelerating reference frame feels identical to a gravitational force.
(D) The period of the orbit as measured by an observer at infinity is 16π M^(1/2) and the period of the orbit as measured by the particle is 16π M^(1/2)(1 + 9/64 M²).
The period of orbit as measured by an observer at infinity can be calculated using the formula: T = 2π R³/2/√(M). Substitute the given values in the above formula: T = 2π (8M)³/2/√(M)= 16π M^(1/2).The period of the orbit as measured by the particle can be calculated using the formula: T = 2π R/√(1-3M/R).
Substitute the given values in the above formula: T = 2π (8M)/√(1-3M/(8M))= 16π M^(1/2)(1 + 9/64 M²).
To know more about Schwarzschild radius
https://brainly.com/question/29534114
#SPJ11
solve -3(x-3)≤ 5(1-x)
Answers
-3x+9<5-5x
The collect the like terms
-3x+5x<5-9
The compute the numbers
2x<-4
The cancel to 2 by 2 to make x only
2x<-4
—- —
2 2
And finally you will find the answer
X=-2
Find the variance of X, where X takes the value 28,46,73,73 with equal probability. ion 5 In the notation xi, the itypically provides you with the:
Answers
The variance of X, where X takes the values 28, 46, 73, and 73 with equal probability, is 364.5.
To find the variance of a random variable X, you need to follow these steps:
1. Calculate the mean (average) of X.
2. Calculate the squared difference between each value of X and the mean.
3. Calculate the expected value of the squared differences.
4. The result obtained in step 3 is the variance of X.
Let’s apply these steps to the given values of X: 28, 46, 73, and 73.
Step 1: Calculate the mean (average) of X.
Mean(X) = (28 + 46 + 73 + 73) / 4 = 220 / 4 = 55
Step 2: Calculate the squared difference between each value of X and the mean.
(28 – 55)^2 = 27^2 = 729
(46 – 55)^2 = 9^2 = 81
(73 – 55)^2 = 18^2 = 324
(73 – 55)^2 = 18^2 = 324
Step 3: Calculate the expected value of the squared differences.
Expected value = (729 + 81 + 324 + 324) / 4 = 1458 / 4 = 364.5
Step 4: The result obtained in step 3 is the variance of X.
Variance(X) = 364.5
Therefore, the variance of X, where X takes the values 28, 46, 73, and 73 with equal probability, is 364.5.
Learn more about Mean here: brainly.com/question/30112112
#SPJ11
Is the slope of the linear function constant? Explain.
Answers
Answer:
Yes. When a function is linear, it means that it will always be a straight line. For this to hold true, the slope must always be constant.
Step-by-step explanation:
Your hospital has just reset the safety stock level for sleeping pills to be 220 pills.
If your hospital consumes an average of 1,155 per day with a standard deviation of 81 pills, what is the chance that your hospital will run out of sleeping pills on any day? (Keep four decimal places in your answer, which should be a number not a percentage)
Answers
The chance that the hospital will run out of sleeping pills on any given day is 0.5000 (or 0.5000 with four decimal places).
To calculate the chance that the hospital will run out of sleeping pills on any given day, we can use the normal distribution and Z-score.
First, let's calculate the Z-score using the formula:
Z = (X - μ) / σ
Where:
X = consumption rate per day (1,155 pills)
μ = average consumption rate per day (1,155 pills)
σ = standard deviation (81 pills)
Z = (1,155 - 1,155) / 81
Z = 0
Now, we need to find the probability associated with this Z-score. However, since the demand for sleeping pills can be considered continuous and not discrete, we need to calculate the area under the curve from negative infinity up to the Z-score. This represents the probability of not running out of sleeping pills.
We discover that the region to the left of a Z-score of 0 is 0.5000 using a basic normal distribution table or statistical software.
To find the probability of running out of sleeping pills, we subtract this probability from 1:
Probability of running out of sleeping pills = 1 - 0.5000
Probability of running out of sleeping pills = 0.5000
Therefore, on any given day, the hospital has a 0.5000 (or 0.5000 with four decimal places) chance of running out of sleeping tablets.
Learn more about probability on:
https://brainly.com/question/23417919
Find the area of the trapezoid.
12
8
6

Answers
Answer:
The area of the trapezoid:
A = (base1 + base2) x height/2
= (6 + 12) x 8/2
= 18 x 4
= 72
Hope this helps!
:)
Ambrose has an indifference curve with equation x2=20-4x^1/2*1. When Ambrose is consuming the bundle (4,16), his marginal rate of substitution is 25/4
Answers
The indifference curve equation given is x2 = 20 - 4x^(1/2)*1, where x1 and x2 represent the quantities of two goods Ambrose is consuming.
The marginal rate of substitution (MRS) measures the rate at which Ambrose is willing to trade one good for the other while remaining on the same indifference curve. It is calculated as the negative ratio of the derivatives of the indifference curve with respect to x1 and x2, i.e., MRS = -dx1/dx2. Given that Ambrose is consuming the bundle (4,16), we can substitute these values into the indifference curve equation to find the corresponding MRS. Plugging in x1 = 4 and x2 = 16, we have: 16 = 20 - 4(4)^(1/2)*1; 16 = 20 - 8; 8 = 8. This confirms that the bundle (4,16) lies on the indifference curve. Now, we are given that the MRS at this point is 25/4.
Therefore, we can set up the following equation: dx1/dx2 = 25/4. Simplifying, we have: dx1/dx2 = -25/4. This indicates that the rate at which Ambrose is willing to trade good x1 for good x2 at the bundle (4,16) is -25/4. The MRS represents the slope of the indifference curve at a given point and reflects the trade-off between the two goods. In this case, it indicates that Ambrose is willing to give up 25/4 units of good x1 in exchange for one additional unit of good x2 while maintaining the same level of satisfaction.
To learn more about curve equation click here: brainly.com/question/28569209
#SPJ11
9, 10, 12, x, 20, 25; The median is 14. Find the value of x.
Answers
x=16
2. Find the distance between point A and point B.
5 units
6 units
7 units
8 units

Answers
You’d count each line going up until you reach the other dot. Or take the number the dot is on and subtract it to the other dots position.
Help me with both please blue is the work and red is the answer

Answers
Answer:
Everything is in the picture above
Step-by-step explanation:
Hope it helps

Drag each label to the correct location on the table. Each label can be used more than once, but not all labels will be used.
Simplify the given polynomials. Then, classify each by its degree and number of terms.

Answers
Answer:
The answers to your questions are given below.
Step-by-step explanation:
Polynomial 1:
12x² + 23x – 2
Name by degree: Quadratic because the highest power in the equation is 2.
Polynomial 2:
7x + 2
Name by number of terms: Binomial because the equation has two terms
Polynomial 3:
12
Name by degree: Constant because it has no variable
Name by number of terms: Monomial because it has only one term.
Find the value of x.

Answers
Answer:
x = 46
Step-by-step explanation:
These 2 angles would add up to 180 degrees.
So 41 + (3x+1) = 180
Let's solve for x.
41 + 3x + 1 = 180
Combine like terms.
42 + 3x = 180
subtract 42 from both sides
3x = 180-42
3x = 138
divide both sides by 3
x = 46
a car manufacturer is looking to compare the sales of their sedan model last year to the sales of the same model 15 years ago at various dealerships. the manufacturer is weighing two different proposals to conduct the study. under the first proposal, the manufacturer randomly samples 10 different dealerships for their sales numbers last year and randomly selects another 10 dealerships for their sales numbers 15 years ago. in the second proposal, the manufacturer randomly samples 10 dealerships for both sets of sales numbers. are the samples in these proposals dependent or independent?
Answers
The samples in the first proposal are independent, while the samples in the second proposal are dependent.
In the first proposal, where the manufacturer randomly samples 10 different dealerships for each set of sales numbers (last year and 15 years ago), the samples are independent. This is because the selection of dealerships for one set of sales numbers does not affect or influence the selection of dealerships for the other set of sales numbers. Each dealership is chosen randomly and independently for each set.
On the other hand, in the second proposal, where the manufacturer randomly samples 10 dealerships for both sets of sales numbers, the samples are dependent. This is because the selection of dealerships for one set of sales numbers is directly tied to the selection of dealerships for the other set of sales numbers. The same 10 dealerships are chosen for both sets, so the samples are not independent.
The choice between independent and dependent samples can have implications for statistical analysis. Independent samples allow for direct comparisons between the two sets of sales numbers, while dependent samples may introduce potential bias or confounding factors due to the shared dealership selection.
Learn more about statistical analysis here:
https://brainly.com/question/14724376
#SPJ11
what is the solution to from the boat of a lake ,the angle of elevation to the cliff is 24.22,if the base of the cliff is 747 feet from the boat ,how high is the cliff to the nearest
Answers
Answer:
Step-by-step explanation:
338.33 ft
3x + 5y =4 What is x, what is y?
Answers
Answer:3x+5y=4
Step-by-step explanation:
Answer:
x=(4/3,0)
y=(0,4/5)
Step-by-step explanation:
Fill The Blank ?We say a definite integral is improper if one ______________is infinite, or if the______________ is infinite.
Answers
We say a definite integral is improper if one or both of the limits of integration is infinite, or if the integrand is infinite.
How to complete the blanksFrom the question, we have the following parameters that can be used in our computation:
The missing blanks
By the definition of definite integral, we have
Improper: If one or both of the limits of integration is infiniteImproper: if the integrand is infinite.Read more about derivatives at
https://brainly.com/question/5313449
#SPJ1
A scale drawing of a school bus has a scale of 1 inch to 10 feet. If the length of the school bus is 2 1/2 inches on the drawing, what is the actual length of the bus?
Answers
Answer: 25 feet
Step-by-step explanation:
Answer:
25 feet
Step-by-step explanation:
10 times 2 is 20 and half of 10 is 5 so 20 and 5 = 25
A truck is 2000 kg and has a cargo load of 1000 kg. Its speed is 50 km/h. The momentum for the truck and cargo is
Answers
Answer:
The momentum for the truck and cargo is 150000 kg·km/h
Step-by-step explanation:
p = mv
p = (2000 kg + 1000 kg)(50 km/h)
p = (3000 kg)(50 km/h)
p = 150000 kg·km/h
What is the surface area of the right cylinder below?A. 509 sq. unitsB. 72 sq. unitsC. 113 sq. unitsD. 622 sq. units

Answers
The surface area of a cylinder is found using the following formula:
\(SA=2\pi r^2+2\pi rh\)Replace for the given values of radius and height:
\(\begin{gathered} SA=2\pi(9)^2+2\pi(9)(2) \\ SA=2\pi(81)+2\pi(18) \\ SA=622 \end{gathered}\)It means that the surface area of the cylinder is 622.
The correct answer is D. 622 sq units.
In ΔIJK, i = 16 inches, j = 22 inches and k=12 inches. Find the area of ΔIJK to the nearest 10th of an square inch.
Answers
Answer:
86.2 in squared
Step-by-step explanation:
Harons formula
Answer:
93.7
Step-by-step explanation:
Sandy used a virtual coin toss app to show the results of flipping a coin 50 times, 400 times, and 2,000 times. Explain what most likely happened in Sandy's experiment.
Sandy's experimental probability was closest to the theoretical probability in the experiment with 2,000 flips.
Sandy's experimental probability was closest to the theoretical probability in the experiment with 400 flips.
Sandy's experimental probability was closest to the theoretical probability in the experiment with 50 flips.
Sandy's experimental probability was exactly the same as the theoretical probability for all three experiments.
Answers
The most likely happened in Sandy's experiment is that,
Sandy's experimental probability was exactly the same as the theoretical probability for all three experiments.
Option D is the correct answer.
What is probability?It is the chance of an event to occur from a total number of outcomes.
The formula for probability is given as:
Probability = Number of required events / Total number of outcomes.
We have,
Tossing a coin:
The probability of getting a head = 1/2
The probability of getting a tail = 1/2
This is the theoretical probability.
Now,
Experiment probability:
Virtual coins too have the same probability of getting a head and a tail as compared to the theoretical probability.
Thus,
Sandy's experimental probability was exactly the same as the theoretical probability for all three experiments.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ1
Answer:Not Sure but it is not D at all so please don't use that!
Step-by-step explanation:
A simple random sample of 500 elements generates a sample proportion p= 0.81. Provide the 90% confidence interval for the population proportion (to 4 decimals). b.Provide 95% the confidence interval for the population proportion (to 4 decimals).
Answers
a) The 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b) The 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
To calculate the confidence intervals for the population proportion, we can use the formula:
Confidence Interval = sample proportion ± margin of error
The margin of error can be calculated using the formula:
Margin of Error = critical value * standard error
where the critical value is determined based on the desired confidence level and the standard error is calculated as:
Standard Error = \(\sqrt{((p * (1 - p)) / n)}\)
Given that the sample proportion (p) is 0.81 and the sample size (n) is 500, we can calculate the confidence intervals.
a. 90% Confidence Interval:
To find the critical value for a 90% confidence interval, we need to determine the z-score associated with the desired confidence level. The z-score can be found using a standard normal distribution table or calculator. For a 90% confidence level, the critical value is approximately 1.645.
Margin of Error = \(1.645 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0323
Confidence Interval = 0.81 ± 0.0323
≈ (0.7777, 0.8423)
Therefore, the 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b. 95% Confidence Interval:
For a 95% confidence level, the critical value is approximately 1.96.
Margin of Error = \(1.96 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0363
Confidence Interval = 0.81 ± 0.0363
≈ (0.7737, 0.8463)
Thus, the 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
Learn more about confidence interval here:
brainly.com/question/32546207
#SPJ4
The figure shows the graphs for functions and .
It is stated that the functions and are determined by:
() = +4
() = 10 − 2x
how do I set up an equation that can be used to determine the first coordinate of the intersection of the graphs?
Answers
Answer:
Step-by-step explanation:
At the point of intersection the coordinate can be found with
10 - 2x = 4 (is the required equation).
Solving this we find the first coordinate (x) to be 3.
Given that X N(300, 15), find the Interquartile Range (IQR) Select one: O a. 310.12 O b. 0.5 O c. 289.99 O d. 20.24.
Answers
The interquartile range (IQR) is found as the 20.24. The correct option is (d) 20.24.
Given that X N(300, 15), find the Interquartile Range (IQR).
The given distribution is normal with mean μ = 300 and standard deviation σ = 15.
We need to calculate the interquartile range (IQR).IQR is defined as the difference between the third quartile (Q3) and the first quartile (Q1).
The first quartile (Q1) is the value below which 25% of the data fall and the third quartile (Q3) is the value below which 75% of the data fall.
We can find these values using the standard normal distribution table.
For the first quartile,
z1 = invNorm(0.25)
= -0.67449
Q1 = μ + σ × z1
= 300 + 15 × (-0.67449)
= 289.88
≈ 289.89
For the third quartile,
z3 = invNorm(0.75)
= 0.67449
Q3 = μ + σ × z3
= 300 + 15 × 0.67449
= 310.12
Therefore, the interquartile range (IQR)
= Q3 – Q1
= 310.12 – 289.89
= 20.23
≈ 20.24
Hence, the correct option is (d) 20.24.
Know more about the interquartile range
https://brainly.com/question/4102829
#SPJ11
Write the ratio of the first measurement to the second measurement. 5 feet to 49 inches
Answers
Answer:
5ft to 49in 5ft/49in 5ft:49in
Step-by-step explanation:
Assume that Verizon Wireless is interested in studying the pricing expectations of its customers. If the study calls for selecting at random 100 people from each of three age groupings, ___________ sampling is being used.
Answers
The correct answer is stratified random sampling.
A type of sampling method where every person in the population has an equal chance of being chosen for the research is known as random sampling.
This sampling method does not require the researcher to divide the population into categories or strata before selecting a sample.
According to the given question, Verizon Wireless is interested in studying the pricing expectations of its customers.
If the study calls for selecting at random 100 people from each of three age groupings, stratified random sampling is being used.
Stratified random sampling is a sampling method in which the researcher divides the population into strata or categories based on some specific variables that the researcher wants to investigate.
In this type of sampling method, a random sample is chosen from each stratum based on some proportionate allocation.
The researcher might divide the population into categories based on age, gender, income, or any other variable relevant to the research question.
Stratification is an effective technique for reducing sampling bias since it guarantees that each stratum is adequately represented in the sample.
Hence, the correct answer is stratified random sampling.
https://brainly.com/question/30759604?referrer=searchResults
#SPJ11
.A system consists of five identical components connected in series as shown:
A system consists of five identical components con
As soon as one components fails, the entire system will fail. Suppose each component has a lifetime that is exponentially distributed with ? = 0.01 and that components fail independently of one another. Define eventsAi = {ith component lasts at least t hours}, i = 1, . . . , 5, so that the Ais are independent events. Let X = the time at which the system fails
Answers
The time at which the system fails, denoted by X, is the minimum of the lifetimes of the five components.
In this system, each component has a lifetime that follows an exponential distribution with a parameter λ = 0.01. The exponential distribution is commonly used to model the time until an event occurs in a system with a constant failure rate.
The probability that a component lasts at least t hours is given by P(Ai) = e^(-λt), where Ai is the event that the ith component lasts at least t hours.
Since the components fail independently of one another, the probability that all five components last at least t hours is the product of their individual probabilities: P(A1 ∩ A2 ∩ A3 ∩ A4 ∩ A5) = e^(-λt)^5 = e^(-5λt).
Now, let X be the time at which the system fails, which is the minimum of the lifetimes of the five components. Since X is the minimum, we can write X = min(T1, T2, T3, T4, T5), where Ti represents the lifetime of the ith component.
The probability distribution of X can be obtained by considering the complement event. The complement of X > t is that all five components last at least t hours, which is P(X > t) = P(A1 ∩ A2 ∩ A3 ∩ A4 ∩ A5) = e^(-5λt).
Therefore, the time at which the system fails, X, follows an exponential distribution with a parameter of 5λ = 0.05. This means that the system has a constant failure rate of 0.05 and the probability density function (pdf) of X is given by f(x) = 0.05 * e^(-0.05x).
Visit here to learn more about probability:
brainly.com/question/31828911
#SPJ11
