The difference in length of a spring on a pogo stick from its non-compressed length when a teenager is jumping on it after 6 seconds can be described by the function#(6) f(theta)= 2cos(theta) + sqrt(3).Part A: Determine all values where the pogo stick's spring will be equal to its non-compressed length. (5 points)Part B: If the angle was doubled, that is theta became 2theta what are the solutions in the interval [0, 211)? How do these compare to the original function? (5 points)Part C: A toddler is jumping on another pogo stick whose length of their spring can be represented by the function g(8) = 1-
Answers
A) Let's begin by writing out the equation for the given condition:
\(\begin{gathered} f(\theta)=2\cos(\theta)+\sqrt{3} \\ 2\cos(\theta)+\sqrt{3}=\sqrt{3} \\ 2\cos(\theta)=0 \\ θ=\frac{\pi }{2}+2\pi n,\:θ=\frac{3\pi }{2}+2\pi n \end{gathered}\)Notice that in part A, we're determining all values in which the pogo stick is equal to its non-compressed length.
B) This part consists in solving the following equation:
\(\begin{gathered} 2\cos \left(2θ\right)+\sqrt{3}=0,\:0\le \:θ<2\pi \\ 2\cos \left(2θ\right)+\sqrt{3}-\sqrt{3}=0-\sqrt{3} \\ 2\cos \left(2θ\right)=-\sqrt{3} \\ \frac{2\cos \left(2θ\right)}{2}=\frac{-\sqrt{3}}{2} \\ \cos \left(2θ\right)=-\frac{\sqrt{3}}{2} \\ 2θ=\frac{5\pi }{6}+2\pi n \\ \frac{2θ}{2}=\frac{\frac{5\pi }{6}}{2}+\frac{2\pi n}{2} \\ θ=\frac{5\pi }{12}+\pi n \\ \\ 2θ=\frac{7\pi }{6}+2\pi n \\ \frac{2θ}{2}=\frac{\frac{7\pi }{6}}{2}+\frac{2\pi n}{2} \\ θ=\frac{7\pi }{12}+\pi n \\ \theta=\frac{5\pi}{12},\:θ=\frac{7\pi}{12},\:θ=\frac{17\pi}{12},\:θ=\frac{19\pi}{12} \end{gathered}\)Note that since the pogo has a periodical movement and an interval was defined then the solutions above are defined for the interval.
Related Questions
Davis burns 1,080 calories when he runs for 2.5 Chours.)The number of calories he burns while
swimming Y)can be described using the
equation y = 266x, where Prepresents the number of hours Davis swims. How many more calories will Davis burn running for 30 minutes) than swimming for 30 minutes assuming the rates remain constant
Answers
Answer:
...
Step-by-step explanation:
To find the number of calories Davis burns while running for 30 minutes, we can use the information that he burns 1080 calories running for 2.5 hours.
We know that 30 minutes is 1/120 of 2.5 hours. So, we can divide the total number of calories by 120 and we get the calorie burn for 30 minutes:
1080 calories / 120 = 9 calories
The number of calories Davis burns while swimming for 30 minutes can be determined by using the equation y = 266x, where x represents the number of hours he swims. We know that he swims for 30 minutes, or 1/120 hours, so we can plug that value into the equation:
y = 266(1/120) = 2.216 calories
So, Davis burns 7 calories more running for 30 minutes than swimming for 30 minutes, assuming the rates remain constant.
A cactus casts a shadow 33 feet long. At the same time of day,Liam,who is 6 feet tall,casts a shadow 9 feet long,as shown. how tall is the cactus
Answers
If x = 2, y = 6, and z = 4, which expression is equivalent to 4? à 54+0-3+2=4. D Xtra 4 ... A tree is 12 feet tall and casts a shadow 9 feet long. A building nearby.
Yesterday, Jack drove 20 miles in his car. Today, Jack drove 15 miles in his car. What is the percent decrease of the time spend driving the car?
Answers
The percentage change will be 25%.
What is the percentage?According to its definition, a percentage is any number relative to 100. It is shown with the sign %. "Out of 100" is what the percentage means. Consider dividing any quantity or item into 100 identical bits.
Using these estimates, we can calculate the per cent decrease in the time spent driving as follows:
The initial time spent driving was 0.5 hours.
The final time spent driving was 0.375 hours.
The decrease in time spent driving was 0.5 - 0.375 = 0.125 hours.
The per cent decrease in time spent driving is,
P = (0.125/0.5) x 100%
P = 25%.
Therefore, we can estimate that the per cent decrease in the time Jack spent driving his car is 25%.
To know more about percentages follow
https://brainly.com/question/24304697
#SPJ1
help asap math question

Answers
The equations that represent the largest number of x desks, y coffee tables, and z corner tables that can be made are
50x + 30y + 5z = 690
40x + 15y + 5z = 620
45x + 10y + 5z = 510
Writing Linear equationsFrom the question, we are to determine the three equations that are needed to find the largest number of x desks, y coffee tables, and z corner tables that can be made
From the given information,
Desks use 50 units of wood, 40 units of fabrics, and 45 units of stuffing
Coffee tables use 30 units of wood, 15 units of fabrics, and 10 units of stuffing
Corner tables use 5 units of wood, 5 units of fabrics, and 5 units of stuffing
Also,
There are 690 units of wood, 620 units of fabric and 510 units of stuffing available to make the items
Thus,
The equations that represent the largest number of x desks, y coffee tables, and z corner tables that can be made are
50x + 30y + 5z = 690
40x + 15y + 5z = 620
45x + 10y + 5z = 510
Learn more on Writing linear equations here: https://brainly.com/question/20696003
#SPJ1
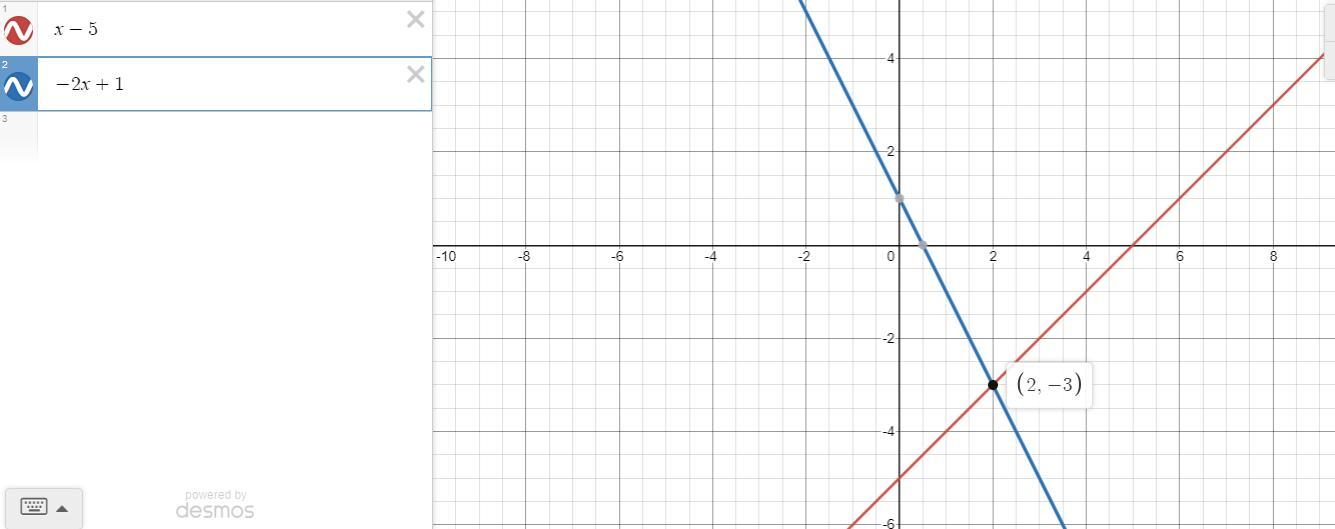
Find where the lines intersect. Y = x - 5 & y = -2x + 1
Answers
We want to find where the two lines intersect
\(\begin{gathered} y=x-5 \\ \text{and} \\ y=-2x+1 \end{gathered}\)Solution
We will subtitute equation 1 into equation 2 ( since y is already made the subject)
From (1)
\(y=x-5\)Put into (2), from (2)
\(\begin{gathered} y=-2x+1 \\ x-5=-2x+1 \\ \text{collect like terms} \\ x+2x=1+5 \\ 3x=6 \\ x=\frac{6}{3} \\ x=2 \end{gathered}\)We substitute the value of x into (1)
From (1)
\(\begin{gathered} y=x-5 \\ y=2-5 \\ y=-3 \end{gathered}\)Therefore, the point is intersection is (2, -3) or the line intersect at x = 2 and y = -3
The graph below further show this claim
Q7 PLEASE HELP ME !!!!!!!!!!!!!!!!!!!



Answers
The outcomes that are contained in the events are
X = 3 and 10 ⇒ P(X) = 1/5Not X =1, 2, 4, 5, 6, 7, 8 ⇒ P(Not X) = 4/51 - P(X) = 4/5 and 1 - P(X) is the same as P(Not X)
The outcomes contained in the eventsFrom the question, we have the following parameters that can be used in our computation:
X = gray colours
Given that
gray colours = 3 and 10
We have
X = 3 and 10
Not X =1, 2, 4, 5, 6, 7, 8
The probability is then calculated as
P(X) = 2/10 = 1/5
For P(Not X), we have
P(Not X) = 1 - 1/5 = 4/5
The equation of P(Not X)In (a), we have
P(Not X) = 1 - 1/5 = 4/5
This means that
P(Not X) = 1 - P(X)
So, the solution is
1 - P(X) = 4/5
The equivalent expressionUsing the above (a) and (b) as a guide, we have the following:
1 - P(X) is the same as P(Not X)
Read more about probability at
https://brainly.com/question/251701
#SPJ1
Celeste is planting a rectangular flower garden in which the width will be 4 feet less than its length. She has decided to put a birdbath within the garden that will occupy a space 3feet by 4 feet how many feet are now left for planting? Express your answer on factored form
Answers
Answer:
(L-6)(L+2)
Step-by-step explanation:
Let L be the length of the flower garden.
Then the width will be L-4.
The area of the flower garden = L*(L-4) =L²-4L
The area of the birdbath is 3*4 = 12 ft²
The area of the remaining space for planting is
= Area of flower garden - area of birdbath
L² - 4L - 12We can factor the expression as follows:
L² - 4L - 12 L²-(6-2)L-12L²-6x+2x-12taking common frome each two terms
L(L-6)+2(L-6)(L-6)(L+2)Therefore, the number of feet left for planting is (L-6)(L+2) in factored form.
c3+c2 factories fully
Answers
Answer:
c6 i guess
Step-by-step explanation:
c^2 (c+1)
convert to slope intercept form
: x- 2y=-6
Answers
Answer:
x-2y =6
x-2y =6
= 6-2y=x=4
A television is on sale for 20% off. If the sale price is $399, what was the original price?
A. $319.20
B.$1,995
C. $498.75
D. $379.00
Answers
Answer:
\(\$498.75\)
Step-by-step explanation:
Let \(x\) be the original price of the item. We can set up the following equation:
\(x\cdot (1-0.2)=399\).
Solving for \(x\), we get:
\(x\cdot 0.8=399,\\x=\frac{399}{0.8},\\x=\fbox{$\$498.75$}\).
Need help with my geometry homework grade due to

Answers
The surface area of the base ball to the nearest whole number is 26 in²
What is surface area of a sphere?A sphere is defined as the set of all points in three-dimensional Euclidean space that are located at a distance.
The area occupied by a three-dimensional object by its outer surface is called the surface area.
The surface area of a sphere is expressed as;
SA = 4πr²
where r is the radius and it's calculated as;
C = 2πr
9 = 2πr
r = 4.5/π =
SA = 4 π × (4.5/π)²
SA = 81/π
SA = 26 in²( nearest whole number)
Therefore the surface area of the sphere is 26 in²
learn more about surface area of sphere from
https://brainly.com/question/16519513
#SPJ1
Math
order of operations-Basic four operators
6x8-12divedby3+ 9
Answers
Answer:
21
Step-by-step explanation:
6 times 8 = 48-12=36 divided by 3 =12+9=21
Solve for 1/4 of x is 6

Answers
Answer: x=24
Step-by-step explanation:
1/4x=6x=6/0.25x=24Other way to do it is 6x4=24Shawn downloads movies at a base price of $2 per movie. If he downloads 5 movies, he will get a 25% discount. How much will Shawn save on the base price if he downloads 5 movies?
Answers
Answer:
$7.50
Step-by-step explanation:
10/4=2.5
10-2.5=7.5
Answer:
$2.50 will be saved
Step-by-step explanation:
Just took the test!
Relative intensity of 9 decibels is how many times higher than that of 8 decibels
Answers
Answer:
what do you mean by land ?
The intensity of sound is proportional to the square of its amplitude.
Thus, if I9 and I8 are the intensities of sounds at 9 decibels and 8 decibels respectively, then:
I9/I8 = (10^(9/10))/(10^(8/10))
I9/I8 = 10^(0.1)
I9/I8 = 1.2589
Therefore, the relative intensity of 9 decibels is approximately 1.26 times higher than that of 8 decibels.
May I please have a Brainliest? I put a lot of thought and effort into my answers, so I would really appreciate it!
Shown below is a regular pentagon inscribed in a circle. Calculate the area of the shaded region. Round your answer to the nearest tenth.

Answers
Answer:
S(a) = 27,5036 squared units
Step-by-step explanation:
Shaded area is :
S(a) = Area of the circle - area of the regular pentagon (1)
A(c) = area of the circle
A(c) = π*(r)² ⇒ A(c) = π*(6)² ⇒ A(c) = 36*π ⇒ A(c) = 113,0976 squared units
Area of a regular pentagon:
a) If we draw a straight line between the center and each vertex we get 5 triangles, and if we draw the apothem for each side, we get 10 triangles. We will calculate the area of one of these triangles
The first 5 triangles has a central angle equal to 72⁰ according to:
360/5 = 72
When we divide these triangles in two triangles by means of the apothem, each central angle will be of 36⁰, then
sin 36⁰ = 0,58778 and cos 36⁰ = 0,809017 and sin 36⁰ = x/6 here x is half of the side of the regular pentagon. Then
0,58778 = x/6
x = 6*0,58778
x = 3,52668 units of length
and cos 36⁰ = a/6 where a is the apothem, then
0,809017 = a / 6 ⇒ a = 6*0,809017
a = 4,8541 units of length
Now we are in conditon to calculate area of the triangles as:
A(t) = (1/2)*b*h
A(t) = (1/2)*x*a ⇒ A(t) = 0,5* 3,52668*4,8541
A(t) = 8,5594 squared units
Finally we have 10 of these triangles, then
Area of regular pentagon is : 10*A(t) squared units
A(p) = 85,594 squared units
Now plugging these values in equation (1) we get the shaded area
S(a) = 113,0976 - 85,594
S(a) = 27,5036 squared units
Estimate the volume of a cube with a side length of 19.9ft
Answers
7880.6 ft cubed
Since it is a cube, we know the side lengths are all the same, and the equation for volume is V = \((sidelength)^{3}\). Therefore we can set up an equation:
V = \((19.9)^{3}\) = 7880.6
Find the LCM of 20, 35 & 50.
Answers
Answer:
Answer: LCM of 20,35 and 50 is 1400
Step-by-step explanation:
50 students in the fourth grade class list of their hair and eye colors in the table below are the events green eyes and brown hair independent
Answers
Answer:
câu này là 500 nhen
The function h(x) is a transformation of the square root parent function,
f(t) = t. What function is H(x)?

Answers
Answer:
A. \(h(x)=\sqrt{x-3}\)
Step-by-step explanation:
Step 1: DefinitionThe parent function of \(\sqrt{x}\) is translated to the left when \(h\) is positive in the transformation \(\sqrt{x+h}\).
If \(h\) is negative, the graph translates towards the left with the distance equal to the value of \(h\).
Step 2: ImplementationHere the graph moved 3 units towards the right. This means that \(h\) is negative and has the value of 3.
So, plugging that into the parent function for translation, the function becomes:
\(h(x)=\sqrt{x-3}\)
show that the volume of the unit cube is one
Answers
Check the picture below.

The diagrams shows a quadrilateral ABCD with each of its sides extended
AB=AD
show the ABCD is a kite

Answers
Answer:
steps attached
Step-by-step explanation:

Answer:
Step-by-step explanation
Ab = 29
373+68=7
Evaluate the line integral, where C is the given curve. (x 9y) dx x2 dy, C C consists of line segments from (0, 0) to (9, 1) and from (9, 1) to (10, 0)
Answers
You have some missing symbols, so I'm guessing that the integral reads
\(\displaystyle \int_C (x-9y) \, dx - x^2 \, dy\)
where C is composed of the two line segments,
• C₁ = {(9t, t) : 0 ≤ t ≤ 1}
• C₂ = {(9 + t, 1 - t) : 0 ≤ t ≤ 1}
The integrals over each path are
\(\displaystyle \int_{C_1} (x-9y) \, dx - x^2 \, dy = \int_0^1 (9t - 9\cdot t) (9 \, dt) - (9t)^2 \, dt\)
\(\displaystyle \cdots = -81 \int_0^1 t^2 \, dt\)
\(\displaystyle \cdots = -\frac{81}3 (1^3 - 0^3) = -27\)
and
\(\displaystyle \int_{C_2} (x-9y) \, dx - x^2 \, dy = \int_0^1 ((9 + t) - 9(1 - t)) \, dt - (9 + t)^2 (-dt)\)
\(\displaystyle \cdots = \int_0^1 (81 + 28t + t^2) \, dt\)
\(\displaystyle \cdots = 81 (1 - 0) + 14 (1^2 - 0^2) + \frac13 (1^3 - 0^3) = \frac{286}3\)
Then the overall line integral has a value of
\(\displaystyle \int_C (x-9y) \, dx - x^2 \, dy = -27 + \frac{286}3 = \boxed{\frac{205}3}\)
Please explain how to solve this

Answers
The solution to the variables are x = 7 and y = 4
How to determine the solution to the variables?From the question, we have the following parameters that can be used in our computation:
Shape = Triangle
The marks on the triangles imply that
The visibly smaller triangle is an equilateral triangleThe other triangle is an isosceles triangleSo, we have the following representation
3x - 5 = 5y - 4
3x - 5 = y + 12
Substitute 3x - 5 = y + 12 in 3x - 5 = 5y - 4
y + 12 = 5y - 4
Evaluate the like terms
4y = 16
So, we have
y = 4
Substitute y = 4 in 3x - 5 = y + 12
3x - 5 = 4 + 12
So, we have
3x = 21
This gives
x = 7
Hence, the values are x = 7 and y = 4
Read more about triangles at
https://brainly.com/question/14285697
#SPJ1
Find the length of an arc on a circle whose radius is 10 cm and whose central angle subtends a central angle of 20º
Answers
Reason: this is because the equation for finding the length of arc it is πxd (pie times diameter) and if you are given an angle it is the - size of the angle/360 times π times diameter -
So,
Because you are given the radius you have to do 10x2 =20cm which is the diameter.
Now, you have to do,
20/360 x π x 20
= 3.4906585…
And you generally round up to 2dp
So it would be
3.49cm
Given the function
f(x) = { 9x+5 x < 0 ,
9x+10 x>0
Calculate the following values
f(-1)=
f(0) =
f(2) =

Answers
Answer:
-1<0 then 9x+5
f(-1)=9*-1+5
f(-1)=-9+5= -4
f(0)=9x+10
f(0)=10
f(2)=9x+5=28
Any help please thank you I appreciate it

Answers
Answer:
114.8 degrees
Step-by-step explanation:
supplementary angles basically means angles equal to 180 degrees
Skye's Ice Cream Shoppe is Mario's favorite place to get ice cream. Unfortunately, because he was late arriving, his friends had already ordered. He did not know what they had ordered for him. They told him that is was either a waffle cone or a sundae and that the ice cream flavor was apricot, chocolate, or blackberry.
What is the probability he will get a sundae?
A.25%
B. 85%
C. 50%
D.90%
Answers
Answer:
C. 50%
Step-by-step explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
They told him that is was either a waffle cone or a sundae
Two options, one of which is a sundae
So 1/2 = 0.5 = 50% probability he will get a sundae, and the answer is given by option C
a) What is the area of the top face of this
cuboid?
b) What is the area of the bottom face of
this cuboid?
4 cm
9 cm
7 cm
Answers
The area of both the top face and the bottom face of the cuboid is 63 square centimeters (cm²).
To find the area of each face of the cuboid, we'll use the formulas for finding the area of a rectangle (which is the shape of each face of the cuboid).
Given dimensions:
Length (L) = 9 cm
Width (W) = 7 cm
Height (H) = 4 cm
a) Area of the top face of the cuboid:
The top face is a rectangle with dimensions 9 cm (length) and 7 cm (width).
Area = Length × Width
Area = 9 cm × 7 cm
Area = 63 square centimeters (cm²)
b) Area of the bottom face of the cuboid:
The bottom face is also a rectangle with dimensions 9 cm (length) and 7 cm (width).
Area = Length × Width
Area = 9 cm × 7 cm
Area = 63 square centimeters (cm²)
Therefore, the area of both the top face and the bottom face of the cuboid is 63 square centimeters (cm²).
To know more about cuboid here
https://brainly.com/question/26403859
#SPJ2
Calculator What is the area of a sector with a central angle of 144° and a radius of 11 cm? Use 3.14 for π and round your final answer to the nearest hundredth. Enter your answer as a decimal in the box. cm² K
Answers
Rounding to the nearest hundredth, the area is approximately 151.976 cm².
The formula for the area of a sector is:
A = (θ/360) x πr²
where θ is the central angle in degrees, r is the radius, and π is pi (3.14).
Plugging in the given values, we get:
A = (144/360) x 3.14 x 11^2
A = 0.4 x 3.14 x 121
A = 151.976
To learn more about the area;
https://brainly.com/question/27683633
#SPJ1