The Bells obtain a 25-year, $150,000 conventional mortgage at a 10.0% rate on a house selling for $190,000. Their monthly mortgage payment, including principal and interest, is $1363.50. They also pay 3 points at closing.

Answers
the Bells will pay a total of $4,914,300 for their house. the Bells will pay a total of $4,770,000 in interest (including the 3 points) over the life of the loan.The Bells' first mortgage payment of $113.50
The solution of the sub parts are as follows :-
a) To determine the total amount the Bells will pay for their house, we need to calculate the amount they will pay in mortgage payments over the life of the loan, as well as the amount they paid in points at closing.
First, we can calculate the total amount of principal and interest they will pay over the life of the loan. We know that their monthly mortgage payment is $1363.50, so the annual payment would be:
$1363.50 x 12 = $16,362
Over the life of the 25-year loan, they will make a total of:
25 x 12 = 300 payments
So the total amount they will pay in principal and interest is:
$16,362 x 300 = $4,908,600
Next, we can calculate the amount they paid in points at closing. We know that they paid 3 points on a $190,000 house, so the amount of points paid is:
3% x $190,000 = $5,700
Therefore, the total amount the Bells will pay for their house is:
$4,908,600 + $5,700 = $4,914,300
Therefore, the Bells will pay a total of $4,914,300 for their house.
b) To determine how much of the cost will be interest (including the 3 points), we can subtract the amount of principal they will pay over the life of the loan from the total amount they will pay. We know that the total amount they will pay is $4,914,300, and we already calculated the amount they will pay in principal:
$150,000
So the amount of interest they will pay is:
$4,914,300 - $150,000 = $4,764,300
In addition, we need to add the amount they paid in points to the interest amount:
$4,764,300 + $5,700 = $4,770,000
Therefore, the Bells will pay a total of $4,770,000 in interest (including the 3 points) over the life of the loan.
c) To determine how much of the first payment on the mortgage is applied to the principal, we can use an amortization schedule or formula. The amortization formula for a fixed-rate mortgage is:
P = (r * A) / (1 - (1 + r)^(-n))
where P is the monthly payment, r is the monthly interest rate (which is the annual rate divided by 12), A is the initial loan amount, and n is the total number of payments.
Using the values given in the problem, we can plug them into the formula to solve for the amount of the first payment that is applied to the principal:
r = 0.10 / 12 = 0.008333 (monthly interest rate)
A = $150,000 (initial loan amount)
n = 300 (total number of payments)
P = ($1363.50)
P = (0.008333 * $150,000) / (1 - (1 + 0.008333)^(-300))
P = $1363.50
Therefore, the total amount of the first payment is $1363.50, and we can calculate the amount of the payment that is applied to the principal by subtracting the interest portion. The interest portion can be calculated by multiplying the monthly interest rate by the outstanding balance:
Interest = 0.008333 * $150,000 = $1250
So the amount of the first payment that is applied to the principal is:
$1363.50 - $1250 = $113.50
Therefore, the Bells' first mortgage payment of $113.50
To know more about interest visit :-
https://brainly.com/question/25793394
#SPJ1
Related Questions
A band played an encore at 2 of its last 4 shows. Considering this data, how many of the
band's next 14 shows would you expect to have an encore?
shows
Answers
The number of times that the band played an encore at 7 out of the next 14 shows.
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The band should do an encore at a rate of 2 out of every 4 gigs, or 2/4 = 1/2 shows, according to the available statistics.
We may use the following percentage to determine how many of the following 14 performances will likely have an encore:
1/2 = x/14
14 = 2x
x = 7
Therefore, we can expect the band to play an encore at 7 out of the next 14 shows.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ2
Which graph shows the information in the table?
Calories in Salad Dressing
Number of Ounces of Salad
Dressing
2
3
4
5
Total Calories
300
450
600
750

Answers
Answer: Number 2
Step-by-step explanation: yes
1. What would the slope of a line that is parallel to the line in the graph be?
(4,3)
X

Answers
keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the line above, since a parallel line will have the same slope anyway
\((\stackrel{x_1}{4}~,~\stackrel{y_1}{3})\qquad (\stackrel{x_2}{1}~,~\stackrel{y_2}{-1}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-1}-\stackrel{y1}{3}}}{\underset{run} {\underset{x_2}{1}-\underset{x_1}{4}}} \implies \cfrac{ -4 }{ -3 } \implies {\Large \begin{array}{llll} \cfrac{ 4 }{ 3 } \end{array}}\)
If y(x) is the solution of the differential equation
\( \rm{xdy - ( {y}^{2} - 4y)dy = 0 \: for \: x > 0, \: \: \: \: \: \: \: y(1) = 2,}\)
& the slope of the curve y=y(x) is never zero, then the value of \(\rm{10y( \sqrt{2} )}\) is
Answers
I assume the equation is
\(x \, dy - (y^2 - 4y) \, dx = 0\)
since separating variables leads to
\(x\,dy = y(y-4) \, dx\)
\(\dfrac{dy}{y(y-4)} = \dfrac{dx}x\)
for which the condition that \(x>0\) is actually relevant, as opposed to the simpler differential equation
\(x \, dx - (y^2-4y)\, dy = 0 \implies y(y-4) \, dy = x \, dx\)
(though it's a bit more work to solve for \(y(x)\) in this case)
That the slope \(\frac{dy}{dx}\) is non-zero tells us that
\(\dfrac{dy}{dx} = \dfrac{y(y-4)}x \neq 0 \implies y\neq0 \text{ and } y \neq 4\)
Integrate both sides.
\(\displaystyle \int \frac{dy}{y(y-4)} = \int \frac{dx}x\)
On the left, expand into partial fractions.
\(\displaystyle \frac14 \int \left(\frac1{y-4} - \frac1y\right) \, dy = \int \frac{dx}x\)
\(\dfrac14 (\ln|y-4| - \ln|y|) = \ln|x| + C\)
With the given initial value, we find
\(y(1) = 2 \implies \dfrac14 (\ln|2-4| - \ln|2|) = \ln|1| + C \implies C = 0\)
so the particular solution is
\(\dfrac14 (\ln|y-4| - \ln|y|) = \ln|x|\)
By definition of absolute value, with the initial condition of \(0 < y=2 < 4\) and the condition \(x>0\), we can remove the absolute values.
\(\dfrac14 (\ln(4-y) - \ln(y)) = \ln(x)\)
Solve for \(y\).
\(\ln\left(\dfrac{4-y}y\right) = 4 \ln(x) = \ln\left(x^4\right)\)
\(\dfrac{4-y}y = \dfrac4y - 1 = x^4\)
\(\implies y(x) = \dfrac4{1 + x^4}\)
Then
\(10y\left(\sqrt2\right) = \dfrac{40}{1 + \left(\sqrt2\right)^4} = \boxed{8}\)
On the off-chance you meant the other equation I suggested, we find
\(\displaystyle \int y(y-4) \, dy = \int x \, dx\)
\(\displaystyle \frac{y^3}3 - 2y^2 = \frac{x^2}2 + C\)
\(y(1) = 2 \implies \dfrac83 - 2\cdot4 = \dfrac12 + C \implies C = -\dfrac{35}6\)
Solving for \(y(x)\) involves picking the right branch of the cube root that agrees with \(y(1)=2\). With the cube root formula, we find
\(y(x) = 2 - \xi(1 - i\sqrt3) - \dfrac1\xi (1+i\sqrt3)\)
where
\(\xi = \dfrac{2\sqrt[3]{4}}{\sqrt[3]{3x^2 - 3 + \sqrt{9x^4 - 18x^2 - 1015}}}\)
With a calculator, we find
\(10y\left(\sqrt2\right) \approx 18.748\)
The histogram shows the number of cell phone calls received by Medera, a middle school student, one Saturday from 10 a.m. to 10 p.m.
A histogram titled Cell Phone Calls has time of day on the x-axis and number of calls on the y-axis. From 10 to 12 pm there were 2 calls; from 12 to 2 pm there were 8 calls; from 2 to 4 pm there were 0 calls; from 4 to 6 pm there were 10 calls; from 6 to 8 pm there were 4 calls; from 8 to 10 pm there were 2 calls.
Which statement most reasonably explains the hours when zero calls were received?
Medera turned the phone off while playing in a soccer game.
Medera’s phone can only receive 22 calls a day.
Medera only receives calls in clusters.
Medera lost her phone for two hours.
Answers
Answer:
Its A. Medera turned the phone off while playing in the soccer game
Step-by-step explanation:
Answer:
It is A.Medera turned the phone off while playing in a soccer game.
Step-by-step explanation:
got a 100 on the test
Is 402 a term of the sequence 8, 13, 18, 23.........?
Answers
Answer:
→402 is not a term in the given sequence.
Step-by-step explanation:
Given sequence is 8,13,18,23,...
First term = 8
Common difference = 13-8= 5
⇛18-13=5
⇛23-18=5
Since the common difference is same throughout the sequence
⇛8,13,18,23,... are in the AP.
Let nth term = 402
We know that
nth term of an AP = an = a+(n-1)d
Now,
an = 402
⇛8+(n-1)(5) = 402
⇛8+5n-5 = 402
⇛5n+3 = 402
⇛5n = 402-3
⇛5n = 399
⇛n = 399/5
n can not be rational number it should be a positive integer.
402 is not a term in the given sequence.
Read more: (5 + 13 + 21 + ......... + 18) = ?
https://brainly.com/question/25888359?referrer
a. Definite integral can be used to calculate percentage rate of change of the function
b. Lorenz curves are special curves used to capture demand elasticity
c. Integration by parts formula is the fundamental formula used to conduct marginal analysis
d. Definite integral can be used to calculate area under a curve in a given interval
Answers
Answer:
d. Definite integral can be used to calculate area under a curve in a given interval
General Formulas and Concepts:
Calculus
Integration
IntegralsArea of a Region Formula: \(\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx\)
Step-by-step explanation:
We know that by definition, an integral is an antiderivative.
Also by definition, an integral is also the area under the curve. This can be extended to area between 2 curves.
We have a formula specifically to find an area under a curve (region), as listed above.
∴ our answer is D.
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration
please help khan academy

Answers
The inequality represented by the graph is given as follows:
y > 3x - 4.
How to define a linear function?The slope-intercept definition of a linear function is given as follows:
y = mx + b.
In which:
The slope m represents the rate of change.The intercept b represents the value of y when x = 0.The graph crosses the y-axis at y = -4, hence the intercept b is given as follows:
b = -4.
When x increases by 1, y increases by 3, hence the slope m is given as follows:
m = 3.
Hence the equation of the line is:
y = 3x - 4.
The inequality is composed by the values to the right (greater) of the line, and has an open interval due to the dashed line, hence:
y > 3x - 4.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Find the equation of the line.
Use exact numbers.

Answers
Answer:
Step-by-step explanation:

If you have a statistical calculator or computer, use it to find the actual sample mean and sample standard deviation. Otherwise, use the values Σx = 2769 and Σx2 = 132,179 to compute the sample mean and sample standard deviation. (Round s to four decimal places.)
Answers
By using a statistical calculator, the actual sample mean and sample standard deviation are:
Actual sample mean = 46.1500.
Actual ample standard deviation = 8.6256.
How to calculate the sample mean for the set of data?In Mathematics and Geometry, the sample mean for any set of data can be calculated by using the following formula:
Mean = ∑x/(n - 1)
∑x represents the sum of all data values.(n - 1) represents the number of data contained in a sample.In Mathematics and Geometry, the sample standard deviation for any set of data can be calculated by using the following formula:
Standard deviation, δx = √(1/N × ∑(x - \(\bar{x}\))²)
x represents the observed values of a sample.\(\bar{x}\) is the mean value of the observations.N represents the total number of of observations.By using a statistical calculator, the actual sample mean and sample standard deviation are as follows;
Actual sample mean = 46.1500.
Actual ample standard deviation = 8.6256.
Read more on standard deviation here: brainly.com/question/14467769
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.


Simplify the expression with nested parentheses.
4 30+ 26+6 −33
Answers
Answer:
not sure if the 4 is seperate but if it is then (30+26)+(6-33)
Step-by-step explanation:
PLEASE HELP ME, ILL GIVE YOU BRAINLIEST

Answers
Answer:
3/2^3=3/8 and (-1/4)^2 = 1/16
Step-by-step explanation:
1. You know what 2^3 is, right? That's 2*2*2. 2*2 is 4, and then 4*2 is 8. So that is 3/8.
2. (-1/4)^2 is (-1/4)*(-1/4), right? So that is (-1*-1)/(4*4). Two negatives make a positive, so -1*-1=1. 4*4 is 16, so we have 1/16.
using the arithmetic sequence 7 10 13 16 find the 6th term of the sequence
Answers
center (-4, -7), tangent to x = 2
Answers
Answer:
(x + 4)^2 + (y + 7)^2 = 36
Step-by-step explanation:
The given information describes a circle with its center at (-4, -7) and tangent to the vertical line x = 2. To determine the radius of the circle, we need to find the distance between the center and the tangent line.
The distance between a point (x1, y1) and a line Ax + By + C = 0 is given by:
d = |Ax1 + By1 + C| / sqrt(A^2 + B^2)
In this case, the equation of the line is x = 2, which can be written as 1x + 0y - 2 = 0. Therefore, A = 1, B = 0, and C = -2. The center of the circle is (-4, -7), so x1 = -4 and y1 = -7. Substituting these values into the formula, we get:
d = |1*(-4) + 0*(-7) - 2| / sqrt(1^2 + 0^2)
d = |-6| / sqrt(1)
d = 6
Therefore, the radius of the circle is 6 units. The equation of a circle with center (h,k) and radius r is given by:
(x - h)^2 + (y - k)^2 = r^2
Substituting the values we have found, we get:
(x + 4)^2 + (y + 7)^2 = 36
This is the equation of the circle that satisfies the given conditions.
Banish Claims that a reflection over the x-axis will carry a circle drawn on a coordinate plane to a circle with the same radius but with a different center. He draws four circles on a coordinate plane below.

Answers
If you do a reflection on the x-axis, you're taking the points from (x , y) to (x , -y).
The only case where the circle won't change its center it is when the center is located at the x-axis(when y = 0).
From the examples given in the question, only the circle C won't change its center.
The answer would be:
Circle A: Support
Circle B: Support
Circle C: Refute
Circle D: Support
please help me answer this question thank you

Answers
Answer:
A
Step-by-step explanation:
8. Write a paragraph proof.
Proof Given: In a plane, a is perpendicular to b, b id perpendicular to c, and c || d.
Prove: a || d
Answers
To prove that line segment a is parallel to line segment d, based on the given information, we can utilize the properties of perpendicular and parallel lines.
Given that a is perpendicular to b and b is perpendicular to c, we know that angles formed between a and b, as well as between b and c, are right angles. Let's denote these angles as ∠1 and ∠2, respectively.
Now, since c is parallel to d, we can conclude that the corresponding angles ∠2 and ∠3, formed between c and d, are congruent.Considering the fact that ∠2 is a right angle, it can be inferred that ∠3 is also a right angle.
By transitivity, if ∠1 is a right angle and ∠3 is a right angle, then ∠1 and ∠3 are congruent.Since corresponding angles are congruent, and ∠1 and ∠3 are congruent, we can deduce that line segment a is parallel to line segment d.
Thus, we have successfully proven that a is parallel to d based on the given information and the properties of perpendicular and parallel lines.
For more such questions on line segment
https://brainly.com/question/30756145
#SPJ8
Which equations are true for x = –2 and x = 2? Select two options x2 – 4 = 0 x2 = –4 3x2 + 12 = 0 4x2 = 16 2(x – 2)2 = 0
Answers
The equations that are true for x = -2 and x = 2 are x² + 4 = 0 and 4x² = 16. So, the correct option is A) and D).
To determine which equations are true for x = -2 and x = 2, we simply substitute these values into each equation and check if the equation is true or not. Here are the results
x² - 4 = 0
Substituting x = -2 gives (-2)² - 4 = 0, which is true. Substituting x = 2 gives 2² - 4 = 0, which is also true. Therefore, this equation is true for both x = -2 and x = 2.
x² = -4
Substituting x = -2 gives (-2)² = -4, which is not true. Substituting x = 2 gives 2² = -4, which is also not true. Therefore, this equation is not true for either x = -2 or x = 2.
3x² + 12 = 0
Substituting x = -2 gives 3(-2)² + 12 = 0, which is true. Substituting x = 2 gives 3(2)² + 12 = 24, which is not equal to zero. Therefore, this equation is true for x = -2 but not for x = 2.
4x² = 16
Substituting x = -2 gives 4(-2)² = 16, which is true. Substituting x = 2 gives 4(2)² = 16, which is also true. Therefore, this equation is true for both x = -2 and x = 2.
2(x - 2)² = 0
Substituting x = -2 gives 2(-2 - 2)² = 0, which is true. Substituting x = 2 gives 2(2 - 2)² = 0, which is also true. Therefore, this equation is true for both x = -2 and x = 2.
Therefore, the two equations that are true for both x = -2 and x = 2 are x² - 4 = 0 and 4x² = 16. So, the correct answer is A) and D).
To know more about substitution:
https://brainly.com/question/30284922
#SPJ1
Solve for x and graph the solution on the number line below.

Answers
The solution of the inequality is 8 ≥ x or x > 10. The graph of the solution is attached
How to solve for x and graph the solution on the number line?An inequality compares two values, showing if one is less than, greater than, or simply not equal to another value e.g. 5 < 6, x ≥ 2, etc.
Solving for x:
11≥ 2x - 5 or 2x - 5 > 15
Collect like terms:
11 + 5 ≥ 2x or 2x > 15 + 5
16 ≥ 2x or 2x > 20
8 ≥ x or x > 10
Note: 8 ≥ x can also be written as x ≤ 8
We can combine the two as follow:
Inequality notation: 8 ≥ x > 10
The graph of the solution is attached
Learn more about inequality on:
brainly.com/question/25275758
#SPJ1

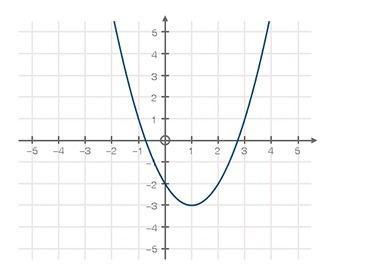
The graph of a function is shown below. Use the graph of the function to find its average rate of change from x=-4 to x=2
Answers
Based on the interval, the average rate of change of the function is 4.0
How to estimate the average rate of change of the function f?The graph that completes the question is added as an attachment
From the graph, we can see that the equation of the graph is a quadratic equation
Also, from the question:
We have the interval to be:
The interval is given as
x = -4 to x = 2
This can be represented as
(a, b) = (-4, 2)
From the attached graph, we have
f(-4) = 22
f(2) = -2
The estimate of the average rate of change f is calculated as(to one decimal place)
Rate = [f(b) - f(a)]/[b - a]
Substitute the known values in the above equation
This gives
Rate = [f(2) - f(-4)]/[2 + 4]
Substitute the known values in the above equation
So, we have
Rate = [-2 - 22]/[2 + 4]
Evaluate
Rate = -4.0
Hence, the estimate (to one decimal place) of the average rate of change of the graph is 4.0
Read more about average rate of change at
brainly.com/question/8728504
#SPJ1
Please solve this
∫ (log(1 + x ^ 2))/((x + 1) ^ 2) dx
Answers
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
We have,
To solve the integral ∫ (log(1 + x²) / (x + 1)²) dx, we can use the method of substitution.
Let's substitute u = x + 1, which implies du = dx. Making this substitution, the integral becomes:
∫ (log(1 + (u-1)²) / u²) du.
Expanding the numerator, we have:
∫ (log(1 + u² - 2u + 1) / u²) du
= ∫ (log(u² - 2u + 2) / u²) du.
Now, let's split the logarithm using the properties of logarithms:
∫ (log(u² - 2u + 2) - log(u²)) / u² du
= ∫ (log(u² - 2u + 2) / u²) du - ∫ (log(u²) / u²) du.
We can simplify the second integral:
∫ (log(u²) / u²) du = ∫ (2 log(u) / u²) du.
Using the power rule for integration, we can integrate both terms:
∫ (log(u² - 2u + 2) / u²) du = log(u² - 2u + 2) / u - 2 ∫ (log(u) / u³) du.
Now, let's focus on the second integral:
∫ (log(u) / u³) du.
This integral does not have a simple closed-form solution in terms of elementary functions.
It can be expressed in terms of a special function called the logarithmic integral, denoted as Li(x).
Therefore,
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
Learn more about integrations here:
https://brainly.com/question/30217024
#SPJ1
Find the measure of BC

Answers
Using central angle theorem,
The measure of the arc BC = 110°.
Define central angle?An angle with its vertex in the middle of the circle it creates with its two radii is said to be central.
Here in the question,
As per the central angle theorem:
(2x -30) ° + x° = 180°
⇒ 2x - 30 + x = 180
⇒ 3x - 30 = 180
Adding 30 on both sides:
⇒ 3x = 180 + 30
⇒ 3x = 210
Dividing both sides by 3.
⇒ x = 70°
Now BC = 2x-30
= 2 × 70 -30
= 140 - 30
= 110°
Therefore, the measure of BC = 110°.
To know more about central angle, visit:
https://brainly.com/question/15698342
#SPJ1
Please awnser asap I am
Stuck

Answers
Answer:
it is too blury to read
Step-by-step explanation:
Help me please I need to do it faster

Answers
Answer:
0.25M + 0.75B + 1.25C - 50 = total money raised
Step-by-step explanation:
0.25 for each muffin so if 78 are sold we do 78*0.25 = 19.5
0.75*56 = 42 for brownies
1.25*30 = 37.5
19.5+42+37.5 = 99
99 -50 = 49
Find the decimal equivalent to :
\(1. \: \: \frac{2}{4} = n\)
\(2. \: \: \frac{4}{9} = n\)
Answers
9514 1404 393
Answer:
0.50.4444444... repeatingStep-by-step explanation:
Your calculator can do this for you.
1. 2/4 = 1/2 = 5/10 = 0.5
__
2. The long division immediately becomes repetitive. The decimal equivalent is repeating 4s: 0.444...
_____
The long division is shown in the attachments. When the remainder is the same as the initial dividend, you know the quotient will repeat.
![Find the decimal equivalent to :[tex]1. \: \: \frac{2}{4} = n[/tex][tex]2. \: \: \frac{4}{9} = n[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/FLVcX5voDOummX8TiNKRwSshVwmZB4oH.png)
![Find the decimal equivalent to :[tex]1. \: \: \frac{2}{4} = n[/tex][tex]2. \: \: \frac{4}{9} = n[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/58tCxC14RhsfGe5owOWXmj7bT6JCIUmQ.png)
The absolute value of 5 is -5.
Answers
Answer:
the absolute value of 5 is 5 and absolute value of -5 is also 5.
Step-by-step explanation:
the absolute value of a number refers to how many spaces away a number is from 0, so it doesn't matter if the number is positive or negative, the absolute value is always positive. the absolute value of -7 is 7, the absolute value of 24 is 24, the absolute value of -435,706 is 435,706, the absolute value of 1,234,567,890 is 1,234,567,890.
i hope this helped :))
which of the following are like radicals? Check all
of the boxes that apply.
3x√√xy
-12x√√xy
-2x√√xj
x-√4x2²
-x√x²y
2√xy
Answers
Answer:
the first 2
Step-by-step explanation:
let me know if it is wrong
Match the following items.
1. y = 2*
2. exponents
3. log 100 = g
4. 0.8395 when log 6,910 = 3.8395
5. 3 when log 6,910 = 3.8395
6. 6,910 when log 6,910 = 3.8395
7. rectangular array of numbers
characteristic
logarithms
antilog
mantissa
common logarithm
matrix
exponential function

Answers
The match for the items are: exponential function, characteristic, common logarithm, mantissa, characteristic, antilog, matrix
How to match the following items
The items in the question can be matched below
Here's the match for the items:
y = 2* ----> exponential function
exponents ----> characteristic
log 100 = g ----> common logarithm
0.8395 when log 6,910 = 3.8395 ----> mantissa
3 when log 6,910 = 3.8395 ----> characteristic
6,910 when log 6,910 = 3.8395 ----> antilog
rectangular array of numbers ----> matrix
Learn more about exponential function at:https://brainly.com/question/2456547
#SPJ1
Find the value of x.

Answers
The value of x when the secant intersect is 5.
How to find the length of secant when they intersect?When two secants intersect outside a circle, the circle divides the secants into segments that are proportional with each other.
Therefore,
(4 + 5)4 = (x - 2 + x + 4)(x - 2)
9(4) = (2x + 2)(x - 2)
36 = 2x² - 4x + 2x - 4
2x² - 2x - 4 - 36 = 0
2x² - 2x - 40 = 0
x² - x - 20 = 0
x² - 5x + 4x - 20 = 0
x(x - 5) + 4(x - 5) = 0
(x + 4)(x - 5) = 0
(x - 5)(x + 4) = 0
x = 5 or x = -4
Therefore,
x = 5
learn more on secant here: https://brainly.com/question/23026602
#SPJ1
what is the slope of the line passing through the points (-3, 4) and (2, -1)
Answers
Answer:
-1
Step-by-step explanation:
You want the slope of the line through the points (-3, 4) and (2, -1).
SlopeThe slope is given by the formula ...
m = (y2 -y1)/(x2 -x1)
Using the given points, we find the slope to be ...
m = (-1 -4)/(2 -(-3)) = -5/5 = -1
The slope of the line through the given points is -1.