The area of a rectangular room is 750 square feet. The width of the room is 5 feet less than the length of the room. Which equations can be used to solve for y, the length of the room? Select three options. y(y + 5) = 750 y2 – 5y = 750 750 – y(y – 5) = 0 y(y – 5) + 750 = 0 (y + 25)(y – 30) = 0
Answers
Answer:
y2−5y=750
750 -y(y-5)=0750−y(y−5)=0 and (y+25)(y-30)=0
Related Questions
need help asap will give brainliest

Answers
vertical shift: 4 units down
Answer: theirs ^
Step-by-step explanation:
The measure of one small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles
Answers
Answer:
x + x - 45 = 90
2x - 45 = 90
2x = 135
x = 67.5, so x - 45 = 22.5
The other two angles measure 22.5° and 67.5°.
Evaluate 8x + 2y if y =6 and x = 3
Answers
Answer:
36
Step-by-step explanation:
Equation:
8(3) + 2(6)
Multiply the co effficent by the variable
8 x 3
8x6
After you add, you get the answer 36.
I would Appreciate the help !!

Answers
Answer:
-3
-2
-1
0
1
2
3
11
314
1729
Step-by-step explanation:
when y = x, it means that whatever x is, that is what y is
so if x is 8, then y is 8
if x is -2, then y is -2
share 660kg in ratio of 5:7
Answers
5x+7x=660;
12x=660;
x=660:12;
x=55 (kg).
Then 5x=5×55=275 kg and 7x=7×55= 385 kg.
The required ratio is therefore
660= 275:385.
Can you help me out?

Answers
1) Unanswered (Sorry)
2) Find the cost of a four-line ad
\(x = 4 \\Therefore,\\c(4) = 30\)
3) Find the cost of a ten-line ad
\(x = 10\\Therefore,\\c(10) = 30 + 5(x - 4)\\c(10) = 30 + 5x - 5(4)\\c(10) = 30 + 5x - 20\\c(10) = 30 + 5(10) - 20\\c(10) = 30 + 50 - 20\\c(10) = 60\)
Which of the following statements is correct about quadratic number patterns? A. The third difference is greater than zero. B. The first difference is constant. C. The difference between terms is always positive. D. The second difference is constant.
Answers
Answer: D.) The second difference is constant.
Step-by-step explanation:
The rate of change of a quadratic function is a linear function. The rate of change of that is constant, so second differences of a quadratic number pattern are constant.
Answer:
D.
Step-by-step explanation:
Which of the following shows the correct solution steps and solution to 2×+ 7 = -11?
Answers
Answer:
x = - 9
Step-by-step explanation:
2x + 7 = - 11 ( subtract 7 from both sides )
2x = - 18 ( divide both sides by 2 )
x = - 9
The answer is:
x = -9
Work/explanation:
The point of equations is to find the variable's value by isolating it step-by-step.
For this equation, the variable is x.
To isolate it, I will perform a few operations.
First, I will subtract 7 from each side:
\(\sf{2x+7=-11}\)
\(\sf{2x=-11-7}\)
\(\sf{2x=-18}\)
Divide each side by 2
\(\sf{x=-9}\)
Hence, x = -9.
\(\rule{350}{4}\)
ANSWER THIS AND ILL LOVE YOU
find angles FAB and BAC

Answers
Answer:
m<FAB = 75°
m<BAC = 105°
Step-by-step explanation:
First, find the value of x.
(13x - 3)° = (3x + 2)° + 55° (exterior angle theorem of a ∆)
Solve for x
13x - 3 = 3x + 2 + 55
13x - 3 = 3x + 57
Collect like terms
13x - 3x = 57 + 3
10x = 60
Divide both sides by 10
x = 6
✔️m<FAB = 13x - 3
Plug in the value of x
m<FAB = 13(6) - 3 = 78 - 3
m<FAB = 75°
✔️m<BAC = 180 - m<FAB (angles on a straight line/supplementary angles)
m<BAC = 180 - 75 (substitution)
m<BAC = 105°
Given m ∥ n, find the value of x.

Answers
given that m is parallel to n,
the angle opposite (2x + 16)° is also (2x + 16)° as vertically opposite angles are equal.
using the corresponding angle rule we know that:
2x + 16 = 96
2x = 80
so x = 40
Juan's mother gave him a recipe for trail mix. What is the order of the ingredients from least to greatest?3/4 cup raisins1/3 cup almonds2/3 cup peanuts1/2 cup cereal
Answers
The answer to question of trail mix in ascending order would be, 1/2 cup cereal, 3/4 cup raisins, 1/3 cup almonds, 2/3 cup peanuts.
The order of ingredients from least to greatest for Juan's trail mix recipe is: 1/2 cup cereal, 3/4 cup raisins, 1/3 cup almonds, and 2/3 cup peanuts. Juan's mother provided the recipe which consists of a combination of dried fruits, nuts, and cereal. The recipe calls for 1/2 cup of cereal, which is the least amount of any of the ingredients. The next ingredient is 3/4 cup of raisins, followed by 1/3 cup of almonds, and finally 2/3 cup of peanuts, which is the greatest amount of any of the ingredients. These ingredients can be combined and enjoyed as a snack.
Hence the answer is, 1/2 cup cereal, 3/4 cup raisins, 1/3 cup almonds, 2/3 cup peanuts.
Click here to learn about ascending order:
brainly.com/question/20681445
#SPJ4
Henry constructed circle A with a radius of 4 units. He then created a sector
as shown in the figure below. Which of the following expressions would help
him find the area of the shaded sector?

Answers
Answer:
C
Step-by-step explanation:
area of circle is found by \(\pi\)\(r^{2}\)
r=4 so 4*4=16
so A=16\(\pi\)
we are finding area of shaded part so 45/360(16\(\pi\))
The area of the shaded sector is (45/360)16π square units if Henry constructed circle A with a radius of 4 units option (C) is correct.
What is a circle?It is described as a set of points, where each point is at the same distance from a fixed point (called the center of a circle)
It is given that:
Henry constructed circle A with a radius of 4 units.
Henry then created a sector as shown in the figure below.
As we know, the area of the sector can be find using the formula:
Area of the sector = (θ/360)πr²
Here, θ is the central angle
r is the radius
π = 3.141
r = 4 units
θ = 45 degrees
A = (45/360)π(4)²
A = (45/360)16π square units
Thus, the area of the shaded sector is (45/360)16π square units if Henry constructed circle A with a radius of 4 units option (C) is correct.
Learn more about circle here:
brainly.com/question/11833983
#SPJ2
it is 4.5 miles from moulton to filby via Burnham and denton how far is it between denton and filby
Answers
Answer: I think that the answer is 3/4 miles
Step-by-step explanation:
Plz help me well mark brainliest!!

Answers
Answer:
x=-52
1/3x-2/3=-18
multiply both sides by 3
x-2=-54
x=-54+2
x=-52
Five pounds of cherries cost $14.95. Write and solve an equation to determine how much each pound of cherries cost.
Answers
Answer:
$2.99 per pound of cherries
Step-by-step explanation:
$14.95 / 5 pounds of cherries = $2.99 per pound of cherries
Explain how to solve 5 x 2 − 3 x = 25 by completing the square. What are the solutions?
Answers
Answer:
\(x = -5\)
Step-by-step explanation:
\(5(2) - 3x = 25\\10 - 3x = 25\\-15 = 3x\\-5 = x\)
Step-by-step explanation:
The solution is shown in the image above

I WILL MARK BRAINLIEST !A line has a slope of 3 and includes the points (7,1) and (4,q). What is the value of q?
Answers
Answer:
q = -8
Step-by-step explanation:
Given the slope and ordered pairs (7, 1) (4, q)
Use slope = 3 and point (7,1) and substitute into the slope-intercept form y = mx + b and solve b
y = mx +b
1 = 3(7) + b
1 = 21 + b
-20 = b
Now write the equation of the line y = 3x - 20
Substitute (4, q) into y = 3x - 20
q = 3(4) - 20
q = 12 - 20
q = -8
Check: Substitute into the slope formula the two ordered pairs (7, 1) (4, -8)
Slope = (change in the y-values)/(change in the x-values)
Slope = (-8 - 1)/(4 - 7)
Slope = (-9)/(-3)
Slope = 3 √
●
Jamie went out to her grandfather's farm.
Her grandfather has pigs and chickens on his farm.
She noticed that there were a total of 26 heads and
68 feet among them. How many chickens and how
many pigs did her grandfather have?
Answers
Answer:
8 pigs
Step-by-step explanation:
Since every animal has only 1 head, a total of 26 heads suggests that there are 26 animals in total.
Suppose all animals are chickens.
Total no. of feet = 26 chickens × 2 feet
= 52 feet
Difference in total no. of feet = 68 feet - 52 feet
= 16 feet
Difference in no. of feet each animal has
= 4 feet (a pig) - 2 feet (a chicken)
= 2 feet
∴ No. of pigs = 16 feet ÷ 2 feet
= 8 pigs
Does anyone know this answer??

Answers
Approximately 99.7% of scores lie in the shaded region.
We have,
The empirical rule, also known as the 68-95-99.7 rule, provides an estimate of the percentage of scores that lie within a certain number of standard deviations from the mean in a normal distribution.
According to this rule:
Approximately 68% of scores lie within 1 standard deviation of the mean.
Approximately 95% of scores lie within 2 standard deviations of the mean.
Approximately 99.7% of scores lie within 3 standard deviations of the mean.
Now,
In the given scenario, the shaded region represents the area between -2 and 3 standard deviations from the mean on the x-axis.
This encompasses the area within 3 standard deviations of the mean.
And,
Since 99.7% of scores lie within 3 standard deviations of the mean, we can estimate that approximately 99.7% of scores lie in the shaded region.
Therefore,
Approximately 99.7% of scores lie in the shaded region.
Learn more about normal distribution here:
https://brainly.com/question/31327019
#SPJ1
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
Find the value of x.
92°
36°
Answers
Answer: the answer is 7°
Step-by-step explanation:
PLEASE HELP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Brandon invests $5800 in two different accounts. The first account paid 3 %, the second account paid 8 % in interest. At the end of the first year he had earned $229 in interest. How much was in each account?
$ ___ at 3 %
$ ____ at 8 %
Answers
Interest is a fee charged by a lender to a borrower for the use of money or credit, usually expressed as a percentage of the amount borrowed or invested over a period of time. Brandon invested $\(4700\) at 3% interest and $\(1100\) at \(8\)% interest. The total interest earned after one year is $229
How much was in each account?
Let x be the amount invested in the first account that pays 3% interest, and let y be the amount invested in the second account that pays 8% interest. Since the total amount invested is $5800, we have:
\(x + y = 5800\)
The amount of interest earned on the first account is 0.03x, and the amount of interest earned on the second account is 0.08y. Since the total interest earned after one year is $229, we have:
\(0.03x + 0.08y = 229\)
We now have two equations with two unknowns:
\(x + y = 5800\)
\(0.03x + 0.08y = 229\)
We can solve for x and y by using elimination or substitution method. Here, we will use the substitution method.
Solve the first equation for x:
\(x = 5800 - y\)
Substitute this expression for x into the second equation and solve for y:
\(0.03(5800 - y) + 0.08y = 229\)
\(174 - 0.03y + 0.08y = 229\)
\(0.05y = 55\)
\(y = 1100\)
Now substitute this value of y into either equation to solve for x:
\(x + 1100 = 5800\)
\(x = 4700\)
Therefore, Brandon invested $\(4700\) at 3% interest and $\(1100\) at \(8\)% interest.
Learn more about the interest here:
brainly.com/question/30393144
#SPJ1
is y=x-3 a function or an equation
Answers
What is the value of y at the y-intercept of the equation 10x + 3y=12.
Answers
Answer:
Y = 4 - \(\frac{10x}{3}\)
Step-by-step explanation:
Move all terms that don't contain y to the right side and solve.
The equation of a line is given by:
y = mx + c
where m is the slope of the line and c is the y-intercept.
The value of y at the y-intercept of the equation 20x + 3y = 12 is 4.
What is an equation of a line?The equation of a line is given by:
y = mx + c
where m is the slope of the line and c is the y-intercept.
Example:
The slope of the line y = 2x + 3 is 2.
The slope of a line that passes through (1, 2) and (2, 3) is 1.
We have,
10x + 3y = 12
We will write the equation in slope-intercept form.
y = mx + c
10x + 3y = 12
3y = 12 - 10x
y = 12/3 - (10/3)x
y = -(10/3)x + 4
4 is the y-intercept.
Thus,
The value of y at the y-intercept of the equation 20x + 3y = 12 is 4.
Learn more about equation of a line here:
https://brainly.com/question/23087740
#SPJ2
write the first five terms of the sequence. an=n2 +2
Answers
I hope this helps

Find the limit: \(\lim_{a x \to 0} \frac{(x + ax)^{2}-2(x + ax) + 1 - (x^{2} - 2x + 1)}{ax}\)
Answers
I'll let h = ax, so the limit is
\(\displaystyle\lim_{h\to0}\frac{(x+h)^2-2(x+h)+1-(x^2-2x+1)}h\)
i.e. the derivative of \(x^2-2x+1\).
Expand the numerator to see several terms that get eliminated:
\((x+h)^2-2(x+h)+1-(x^2-2x+1)=x^2+2xh+h^2-2x-2h+1-x^2+2x-1=2xh+h^2-2h\)
So we have
\(\displaystyle\lim_{h\to0}\frac{2xh+h^2-2h}h\)
Since h ≠ 0 (because it is approaching 0 but never actually reaching 0), we can cancel the factor of h in both numerator and denominator, then plug in h = 0:
\(\displaystyle\lim_{h\to0}(2x+h-2)=\boxed{2x-2}\)
Answer:
2x-2
Step-by-step explanation:
lim ax goes to 0 ( x+ ax)^2 -2 ( x+ax) +1 - ( x^2 -2x+1)
--------------------------------------------------
ax
Simplify the numerator by foiling the first term and distributing the minus signs
x^2+ 2ax^2 + a^2 x^2 -2x-2ax +1 - x^2 +2x-1
--------------------------------------------------
ax
Combine like terms
2ax^2 + a^2 x^2 -2ax
--------------------------------------------------
ax
Factor out ax
ax( 2x + ax -2)
----------------------
ax
Cancel ax
2x + ax -2
Now take the limit
lim ax goes to 0 ( 2x + ax -2)
2x +0-2
2x -2
Find the value of x that makes quadrilateral ABCD a rectangle if BE = 3x+1 and ED = 5x-3

Answers
The value of x that makes quadrilateral ABCD a rectangle if BE = 3x+1 and ED = 5x-3 is x = 2.
What is a rectangle?A quadrilateral with parallel sides that are equal to one another and four equal vertices is known as a rectangle. It is also known as an equiangular quadrilateral for this reason.
Rectangles can also be referred to as parallelograms because their opposite sides are equal and parallel.
There are four vertices and four sides.
Every vertex has an angle of 90 degrees.
Equal and parallel opposed sides are bisected by a diagonal.
We know that the diagonals of a rectangle bisect each other.
Thus, for the quadrilateral to be a rectangle we have:
BE = ED
3x + 1 = 5x - 3
1 + 3 = 5x - 3x
4 = 2x
x = 2
Hence, the value of x that makes quadrilateral ABCD a rectangle if BE = 3x+1 and ED = 5x-3 is x = 2.
Learn more about rectangle here:
https://brainly.com/question/29123947
#SPJ1
Which graph has the same end behavior as f (x) = StartFraction negative 6 x Superscript 5 Baseline minus x cubed + 7 x Over 2 x squared + 1 EndFraction


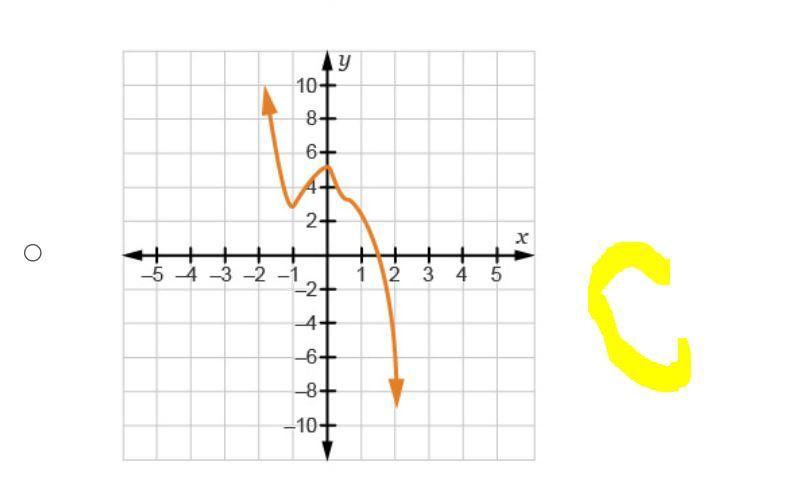

Answers
The graph with the same end behavior is the one in option C.
Which graph has the same end behavior?The given function has a numerator with a negative leading coefficient and an odd degree, while the denominator is a quadratic polynomial.
It will mean that as x tends to negative infinity, the function tends to infinity, and as x tends to positive infinity, the function tends to negative infinty, that is the end behavior of the given function.
The graph with that end behavior is the same one than in option C.
Learn more about end behavior:
https://brainly.com/question/1365136
#SPJ1
pls find prism if you find it your littearly a pro hacker

Answers
Answer:
24 cubic unitsStep-by-step explanation:
Given, in picture,It is a rectangular prism.
It's length in units = 4
It's breadth in units = 2
It's height in units = 3
Therefore,Volume of the given rectangular prism
= length × breadth × height
= 4 units × 2 units × 3 units
= 24 cubic units (Ans)
Find the polar equation of the conic with focus at the pole, directrix y=3 and eccentricity of 2.
Answers
To find the polar equation of a conic with focus at the pole, directrix y=3, and eccentricity of 2, we can use the definition of a conic in polar coordinates.
The general form of the polar equation for a conic with focus at the pole is given by:
r = \(\frac{ed}{1+e\cos(\theta-\theta_0)}\)
Where:
- r is the distance from the origin (pole) to a point on the conic.
- e is the eccentricity.
- d is the distance from the pole to the directrix.
- θ is the angle between the polar axis and the line connecting the pole to a point on the conic.
- θ_0 is the angle between the polar axis and the line connecting the pole to the focus.
In this case, the focus is at the pole, so θ_0 = 0. The directrix is y = 3, which means its distance from the pole is d = 3. The eccentricity is given as 2, so e = 2.
Substituting these values into the general equation, we get:
r =\(\frac{2\cdot3}{1+2\cos(\theta-0)}\)
Simplifying further:
r =\(\frac{6}{1+2\cos(\theta)}\)
Therefore, the polar equation of the conic with focus at the pole, directrix y=3, and eccentricity of 2 is:
r =\(\frac{6}{1+2\cos(\theta)}.\)
This equation describes the shape of the conic in polar coordinates, where r represents the distance from the origin to a point on the conic, and θ represents the angle between the polar axis and the line connecting the origin to the point.
For more such question on polar equation
https://brainly.com/question/9363127
#SPJ8