solve for y. x + a =yb
Answers
Answer:
\(\frac{x+a}{b} = y\)
Step-by-step explanation:
"yb" means multiply so to solve you divide both sides by "b" to get y = x+a/b
Hope that helps and have a great day!
Related Questions
at least 5 significant digits (eg, 3.14159) or use the constant math.pi. you should define a function named soup volume which takes two parameters, the diameter of the can in cm, and the height of the can in cm, in that order. the function should return a float value, which is the volume of soup that the can is able to hold. the function should not round the value, but when printing the value in the main program, format it to show only 2 decimal places. example run of the program: enter the diameter of the can in cm: 5 enter the height of the can in cm: 10 the can holds 186.53 cubic cm of soup.
Answers
This will display the volume of the soup can with only 2 decimal places.
The task requires defining a function named "soup_volume" that calculates the volume of a soup can given its diameter and height, in centimeters. The function should return a float value with at least 5 significant digits, and the main program should print the result formatted to show only 2 decimal places. An example of the program's output would be: "The can holds 186.53 cubic cm of soup" for a can with diameter 5 cm and height 10 cm.
To calculate the volume of the soup can, we can use the formula V = pi * r^2 * h, where pi is the mathematical constant approximately equal to 3.14159, r is the radius of the can (half of the diameter), and h is the height of the can. Thus, we can define the function "soup_volume" in Python as follows:
def soup_volume(diameter, height):
radius = diameter / 2
volume = math.pi * radius ** 2 * height
return volume
To print the result, we can use the input function to prompt the user for the diameter and height of the can, and then call the "soup_volume" function to calculate the volume, and finally format the result using the round function and f-strings, as follows:
diameter = float(input("Enter the diameter of the can in cm: "))
height = float(input("Enter the height of the can in cm: "))
volume = soup_volume(diameter, height)
print(f"The can holds {round(volume, 2)} cubic cm of soup.")
to learn more about diameter click here:
brainly.com/question/5501950
#SPJ11
Prove or disprove the following statement using the definition of Θ : (i) 1∗11+3∗17+5∗23+…+(2n−1)(6n+5)=4n3+8n2−n for all positive integers n (ii) 1+22∗2−1+2∗33∗3−2+3∗44∗4−3+…+n(n+1)(n+1)∗(n+1)−n=n+1−n+11 for all positive integers n
Answers
Since the equation does not hold for n = 1 and n = 2, it does not hold for all positive integers n.
(i) Proving the given statement:
Using the definition of Θ:
Let f(n) = 1∗11+3∗17+5∗23+…+(2n−1)(6n+5), then
f(n) = Θ(n³).
Now, we have to prove 1∗11+3∗17+5∗23+…+(2n−1)(6n+5)=4n³+8n²−n for all positive integers n.
For n = 1, 1(6(1) + 5) = 4 + 8 - 1.
LHS = 11 and RHS = 11.
Hence the equation is true for n = 1.
Now assume that the equation is true for n = k.
1∗11+3∗17+5∗23+…+(2k−1)(6k+5)=4k³+8k²−k ----------- (1)
Now, let's prove for n = k + 1.
1∗11+3∗17+5∗23+…+(2k+1)(6k+11)=4(k+1)³+8(k+1)²−(k+1)
Putting k + 1 in place of k in equation (1),
1∗11+3∗17+5∗23+…+(2k+1)(6k+11)=4k³+12k²+8k+4+8k²+16k+8−(k+1)1∗11+3∗17+5∗23+…+(2k+1)(6k+11)
=4k³+12k²+8k+4+8k²+16k+8−k−11∗11+3∗17+5∗23+…+(2k+1)(6k+11)
=4k³+12k²+8k+4+8k²+16k+8−k−1+1LHS = 1∗11+3∗17+5∗23+…+(2k−1)(6k+5) + (2k+1)(6k+11)
= f(k) + (2k+1)(6k+11)
RHS = 4k³+8k²−k + 4k²+12k+4+4k³+12k²+8k+1
= 8k³+24k²+20k+5
= 4(k+1)³+8(k+1)²−(k+1)
Hence proved.
(ii) Disproving the given statement:
Let's assume that the statement is true for all positive integers n.
Let's put n = 1 in the given equation,
1+22∗2−1+2∗33∗3−2+3∗44∗4−3+…+n(n+1)(n+1)∗(n+1)−n=n+1−n+111 + 2.1/2 + 2.1/6 - 1 + ... + (n(n+1)/(n+1)² - n)
= 1
Now, let's put n = 2 in the given equation.
1+22∗2−1+2∗33∗3−2+3∗44∗4−3+…+n(n+1)(n+1)∗(n+1)−n=n+1−n+111 + 2.1/2 + 2.1/6 - 1 + 2.2/3 + 3.3/8 - 2 + ... + (2.3/9 - 2)
= 2/3
Since the equation does not hold for n = 1 and n = 2, it does not hold for all positive integers n.
Hence disproved.
Learn more about positive integers from the given link
https://brainly.com/question/1367050
#SPJ11
hello do know how sovle surface area
Answers
Answer:
if I know then I will tell
what is the probability that the lifetime of at least one component exceeds 2? (do not round intermediate values. round your answer to three decimal places.)
Answers
The probability that the lifetime of at least one component exceeds 2 is 0.135.
Given that the joint pdf is f(x,y)=xe^(-x(1+y)) for x≥0, y≥0 and 0 otherwise as shown in attached image.
We want to find the probability that the lifetime of at least one component exceeds 2.
The probability that the lifetime of at least one component exceeds 2 is P(X>2).
\(\begin{aligned}P(X > 2)&=\int_{x=2}^{\infty}\int_{y=0}^{\infty}f(x,y)dydx\end\)
Now, we will substitute the given function, we get
\(\begin{aligned}P(X > 2)&=\int_{x=2}^{\infty}\int_{y=0}^{\infty}xe^{-x(1+y)}dydx\end\)
Further, we will simplify this, we get
\(\begin{aligned}P(X > 2)&=\int_{x=2}^{\infty}\left[-e^{-x(1+y)\right]_{0}^{\infty}dx\\ &=\int_{x=2}^{\infty}e^{-x}dx\\ &=\left[-e^{-x}\right]_{2}^{\infty}\\ &=e^{-2}\\ &=0.135\end\)
Hence, the probability that the lifetime of at least one component exceeds 2 for the joint pdf is f(x,y)=xe^(-x(1+y)) for x≥0, y≥0 and 0 otherwise as shown in attached image is 0.135.
Learn more about the joint pdf from here brainly.com/question/15109814
#SPJ4

Vance bought 2 packages of large beads and 1 package of medium beads. He bought 2 packages of large buttons and how many more beads than more buttons did vance buy
Answers
There are 472 more buttons bought by Vance than beads.
Define the term difference of number?One of the most crucial arithmetic operations, that is obtained by removing two integers, produces difference in mathematics.For the stated question table is made.
So,
Total number of beads bought by Vance = Number of beads(2 packages of large beads) + Number of beads(1 package of medium beads).
= (2 × 96) + (1 × 64)
= 2 × (90 + 6) + 64
= (2 × 90) + (2 × 6) + 64
= 180 + 12 + 64
= 256 beads
Now,
Total number of buttons bought by Vance = Total number of buttons (2 packages of large buttons) + Number of buttons (2 packages of medium buttons)
= (2 × 56) + (2 × 38)
= 2 × (50 + 6) + 2 × (30 + 8)
= (2 × 50) + (2 × 6) + (2 × 30) + (2 × 8)
= 100 + 12 + 600 + 16
= 728 buttons
Thus,
Difference for the number of buttons and beads
= 728 – 256
= 472 beads
So,
Therefore, there are 472 more buttons bought by Vance than beads.
Know more about the difference of number, here
https://brainly.com/question/18591813
#SPJ4

What is the equation of the line that passes through the points (1, –1) and (3, –7)
Answers
Answer:
y = -3x + 2
Step-by-step explanation:
To find the slope of an equation you can do (y2-y1)/(x2-x1). Plug the values in from the equation and you get (-1+7)/(1-3), or 6/-2. This means the slope is -3. Then you plug the values of y and x into an equation y = -3x + b, and you get -1 = (-3)1 + b. Solve for b. -1 = -3 + b, (add 3 to each side) 2 = b. Then plug b back into your equation and you get y = -3x + 2
Answer:
-3x+2=y
Step-by-step explanation:
u need to find the slope intercept formula which mx+b=y
m=slope
b=y-intercept
first u should find the slope which is y2-y1/x2-x1
point 1:(1,-1)
point 2:(3,-7)
-7+1/3-1=-6/2=-3
m=-3
now replace the variables
-3(1)+b=-1
-3 times 1=-3
-3+b=-1
add 3 to both sides
b=2
now the equation is -3x+2=y
express the ratio 7day to 6weeks as a decimal fraction

Answers
Answer:
6 weeks=6*7 days=42days
7/42 =1/6 =0.16667
OR
7 days=1 week
therefore 1/6=0.16667
Note that both must be in the same unit.
Names of TV shows taped in New York are an example of which type of data? Answer a. Qualitative b. Statistic c. Quantitative d. Parameter
Answers
Option (A) Names of TV shows taped in New York are an example of qualitative data. Qualitative data is descriptive in nature and does not involve numerical values or measurements.
It deals with qualities or attributes that cannot be expressed numerically. In this case, the names of TV shows are characteristics that describe the nature of the data. Quantitative data, on the other hand, is numerical data that can be measured and expressed in numbers. A parameter is a measurable factor or variable that can be used to define a system, while statistics is a branch of mathematics that deals with data collection, analysis, and interpretation. In conclusion, since the names of TV shows are descriptive in nature and do not involve numerical values, they are an example of qualitative data.
To know more about qualitative data visit :
https://brainly.com/question/29004144
#SPJ11
the total number of sides in 2 regular polygons is 13, and tge titak number of diagonals is 25. how many sides is each polygon
Answers
One polygon has 6 sides and the other has 7 sides.
Polygons are closed 2D shapes made up of straight lines. Regular polygons have sides of equal length and angles of equal measure. In this problem, we are given information about two regular polygons.
We are told that the total number of sides in both polygons is 13. Let's call the number of sides in one polygon "n" and the number of sides in the other polygon "m". Then, we know that:
n + m = 13
Next, we are given the total number of diagonals in both polygons, which we can calculate using the formula:
d = (n(n-3) + m(m-3))/2
where "d" is the total number of diagonals. We are told that d = 25. Substituting this value and the equation for n + m into the diagonal formula, we get:
25 = (n(n-3) + m(m-3))/2
25 = (n² - 3n + m² - 3m)/2
50 = n² - 3n + m² - 3m
We can use the equation n + m = 13 to solve for one variable in terms of the other. For example, we can solve for "m" by subtracting "n" from both sides:
m = 13 - n
Substituting this into the previous equation, we get:
50 = n² - 3n + (13-n)² - 3(13-n)
50 = n² - 3n + 169 - 26n + n² - 36 + 3n
Simplifying this equation, we get:
2n² - 26n + 45 = 0
We can use the quadratic formula to solve for "n":
n = (26 ± √376)/4
n ≈ 5.61 or n ≈ 8.39
Since we are dealing with whole numbers of sides, "n" must be either 6 or 8. Plugging each value into the equation n + m = 13, we find that the other polygon must have the opposite value.
To know more about polygon here
https://brainly.com/question/24464711
#SPJ4
An object has a mass of 450 g and a volume of 6 cm3
find the density of the object in g/cm3.
Answers
Answer:
75g/cm^3Step-by-step explanation:
density of an object is defined as the mass per unit volume of that objectit has the formular: density= mass/volumefrom the question, density= 450/6= 75g/cm^3density= 75g/cm^3suppose the length of maize ears has narrow sense heritability (h2) ( h 2 ) of 0.70. a population produces ears that have an average length of 28 cm c m , and from this population a breeder selects a plant producing 34- cm c m ears to cross by self-fertilization.
Answers
We can expect the mean length of ears in the next generation to be 31.6 cm.
It is given that the narrow sense heritability (h2) is 0.70, which means that 70% of the total variation in maize ear length is due to genetic factors.
Let the mean length of ears in the original population be µ and the mean length of ears in the selected plant be x. Then, we can use the formula for response to selection to find the expected mean length of ears in the next generation:
x' = µ + h2 * (x - µ)
Substituting the given values, we get:
x' = 28 + 0.70 * (34 - 28) = 31.6 cm
Therefore, we can expect the mean length of ears in the next generation to be 31.6 cm.
To know more about mean visit:
brainly.com/question/2046711
#SPJ4
a rectangle is transformed according to the rule r0 90 T/F
Answers
When the rectangle is transformed according to the rule r0 90 T/F, it first undergoes a reflection about the y-axis, followed by a rotation of 90 degrees counterclockwise about the origin, and finally a translation of a certain distance in either the x or y direction depending on whether the final image is a reflection or not.
The final image obtained will be a rectangle as well, but with different dimensions and position depending on the translation distance.Let's assume that the rectangle has width w and height h. When reflected about the y-axis, its width changes sign but its height remains the same, resulting in a new width of -w and height of h.
After that, the rectangle is rotated 90 degrees counterclockwise about the origin, which swaps its width and height but preserves their signs, resulting in a new width of -h and height of -w.
Finally, a translation of distance d is applied to either the x or y coordinate depending on whether the final image is a reflection or not. If the final image is a reflection, then the translation is applied in the y direction by a distance of d, resulting in a new position of (-h, d).
Otherwise, the translation is applied in the x direction by a distance of d, resulting in a new position of (d, -w).In summary, the rectangle is transformed according to the rule r0 90 T/F by undergoing a reflection, rotation, and translation, resulting in a new rectangle with dimensions and position depending on the original dimensions and the translation distance.
Learn more about rectangle from given link,
brainly.com/question/25292087
#SPJ11
A rectangle can be transformed according to the rule r0 90 T/F, which can have different results, depending on how the transformation is done.
The rule can be interpreted as follows:r0: No rotation90: Rotate the rectangle 90 degreesT/F: Flip the rectangle horizontally (T) or vertically (F)For example, if a rectangle with a width of 4 units and a height of 2 units is subjected to this transformation rule, the result will vary depending on the order of transformations.
Consider the following cases : Case 1: r0 90 F T (rotate by 0 degrees, then rotate by 90 degrees, then flip vertically, then flip horizontally) In this case, the rectangle is first rotated by 0 degrees, which means that its position and size are unchanged. Next, it is rotated by 90 degrees, which means that its width becomes its height and vice versa. After that, it is flipped vertically, which means that its top and bottom edges are swapped.
Finally, it is flipped horizontally, which means that its left and right edges are swapped. The resulting rectangle has a width of 2 units and a height of 4 units. It is also reflected across the line y = 0 (the x-axis).Case 2: F T r0 90 (flip vertically, then flip horizontally, then rotate by 0 degrees, then rotate by 90 degrees) In this case, the rectangle is first flipped vertically, which means that its top and bottom edges are swapped. Next, it is flipped horizontally, which means that its left and right edges are swapped.
After that, it is rotated by 0 degrees, which means that its position and size are unchanged. Finally, it is rotated by 90 degrees, which means that its width becomes its height and vice versa. The resulting rectangle has a width of 2 units and a height of 4 units.
It is also reflected across the line y = -x (the line that goes through the origin with a slope of -1).In conclusion, a rectangle can be transformed in various ways, and the order of transformations matters. The rule r0 90 T/F can produce different results depending on the sequence of operations.
To learn more about rectangle , visit
brainly.com/question/25292087
#SPJ11
if ABC = DEC, angle B = 2x, angle C = 48°, and angle D = 74°. x=?
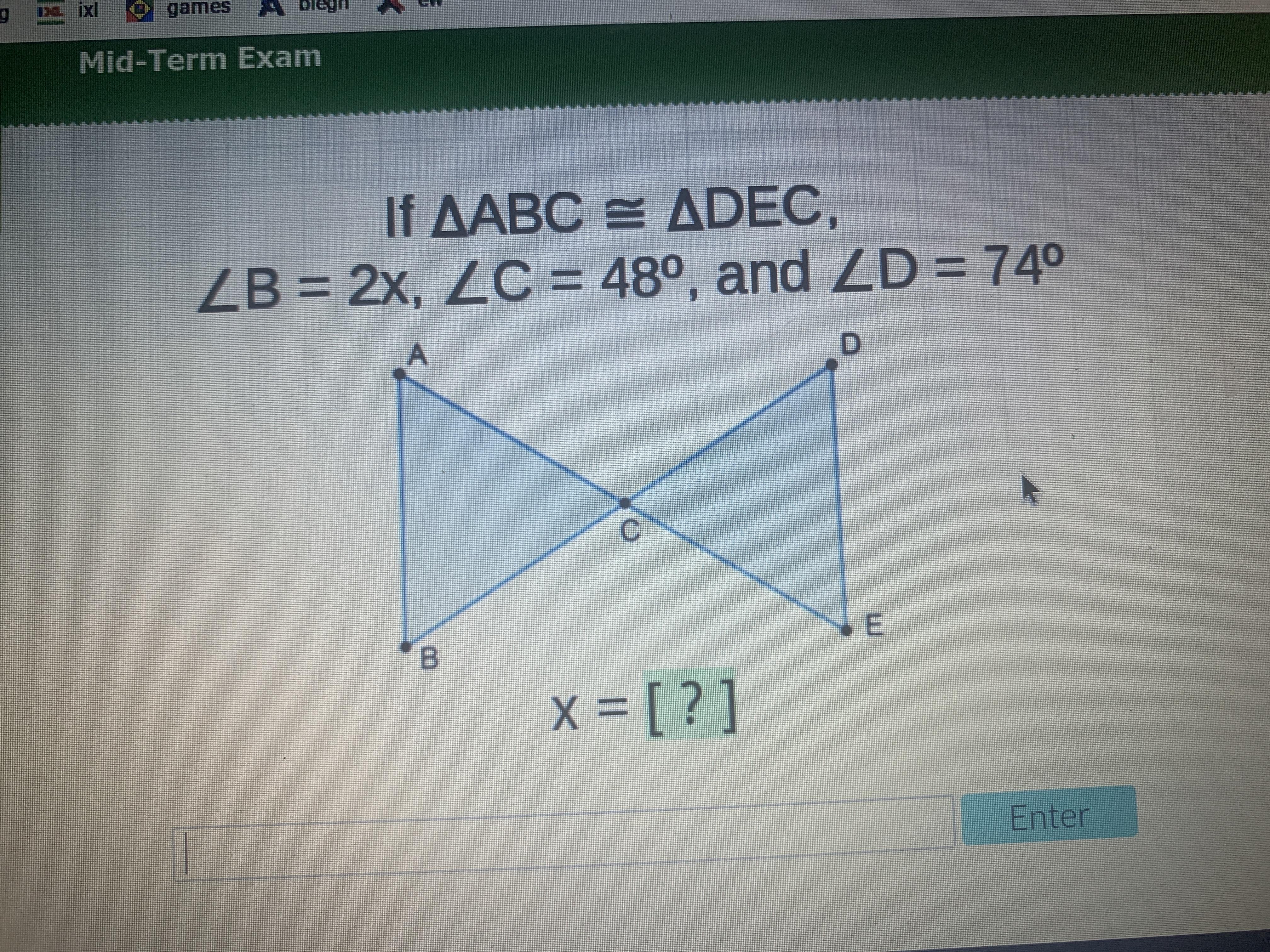
Answers
Answer:
37°
Step-by-step explanation:
angle B = angle D (alternate angle)
2X = 74°
X = 37°
Answer:
29
Step-by-step explanation:
right in acellus
We wish to estimate what percent of adult residents in a certain county are parents. Out of 300 adult residents sampled, 102 had kids. Based on this, construct a 95% confidence interval for the proportion p of adult residents who are parents in this county.
Answers
Answer:
The answer is "\(0.34 \pm 0.060\)".
Step-by-step explanation:
Point estimate = Sample proportion \(= \frac{102}{300}= 0.34\)
For \(95\%\) confidence, \(z = 1.96\)
Hence,
Margin of error\(= 1.96 \times \sqrt{0.34\times \frac{0.84}{300}}=1.96 \times 0.0308 = 0.060\)
Therefore,
Confidence interval in the tri-equality form:
\(\to 0.34 - 0.060 < p < 0.34 + 0.060\\\\\to 0.28 < p < 0.4\)
Confidence interval using point estimate and margin of error:
\(p = 0.34 \pm 0.060\)
Determine the third velocity component v such that all the components satisfy the continuity equation. The two components are as follows: u = 2xt-3xyz + 4xy w = 3x-5yzt+yz Also find the velocity and acceleration of a fluid particle at (1, 0, 1) at time, t= last digit.
Answers
The given velocity components are:
u = 2xt - 3xyz + 4xyw = 3x - 5yzt + yz
To satisfy the continuity equation, the third velocity component must be of the form
v = -ux - wy
Thus,v = -2xt + 3xyz - 4xy (from u)v = -3x + 5yz t - yz (from w)
The third velocity component
v = -2xt + 3xyz - 4xy - 3x + 5yz t - yz
= -2xt + 3xyz - 4xy - 3x + 5yz (t - 1)
The velocity of the fluid particle is given by,
v = (u, v, w) = (2t, -2t + 3z, 3 - 5zt + y)at (1, 0, 1) and t = 1 (last digit),v = (2, -2, -2)
The acceleration of the fluid particle is given by,
a = (at, av, aw)
= (∂u/∂t, ∂v/∂t, ∂w/∂t)at (1, 0, 1) and t = 1 (last digit),a = (2, 3, -5)
To know more about particle visit:
https://brainly.com/question/13874021
#SPJ11
if y varies jointly as x and the inverse of z and y = -5 and x = -5 and z = 6, find y when x = 5 and z = -8
Answers
Step-by-step explanation:
y varies inversely as x=
y= k/xz
-5= k(-5)/6
k= 6
y=6/xz
y=6/5×-8
y= -3/20
pls tell me which one it is

Answers
Answer:
X = 50
Step-by-step explanation:
Both equations TOGETHER equal 180 degrees so you write the equation:
2x + 30 + x = 180
(combine X's. Subtract 30 from both sides):
3x = 150
(divide both sides by 3)
X = 50
x2–6x + 10 is to be written in the form ( x +a)2+ b Find the values of a and b.
Answers
Answer:
a = -3 and b = 1
Step-by-step explanation:
x² - 6x + 10
→ Half the second term and place it in the bracket
( x - 3 )²
→ Square -3
- ( 3 )² = -9
→ Place this outside the brackets along with plus 10
( x - 3 ) ² - 9 + 10
→ Simplify
( x - 3 ) ² + 1
you roll a six-sided die. find the probability of the event described. explain your reasoning: you roll a number less than three
Answers
1/6 + 1/6 = 2/6
Or 1/3 simplified
COS X/1+sinx = sec x-tan x
Answers
Hello there. To solve this question, we'll have to remember some properties about trigonometric functions.
Given the expression:
\(\dfrac{\cos(x)}{1+\sin(x)}\)We want to show that it is equal to
\(\sec(x)-\tan(x)\)First, multiply the fraction by the following expression
\(\begin{gathered} \dfrac{1-\sin(x)}{1-\sin(x)} \\ \end{gathered}\)We choose this fraction for two reasons:
It does not change the expression, since we're multiplying it by 1
It will help in rewrite the expression in the denominator, using a product rule.
Okay. Multiplying the fractions, we get
\(\dfrac{\cos(x)}{1+\sin(x)}\cdot\dfrac{1-\sin(x)}{1-\sin(x)}=\dfrac{\cos(x)\cdot(1-\sin(x))}{(1+\sin(x))\cdot(1-\sin(x))}\)In the denominator, apply the rule of the product between the sum and difference:
\((a+b)(a-b)=a^2-b^2\)Hence we have
\(\dfrac{\cos(x)\cdot(1-\sin(x))}{1-\sin^2(x)}\)Using the fundamental trigonometric identity
\(\cos^2(x)+\sin^2(x)=1\)We write
\(\cos^2(x)=1-\sin^2(x)\)Therefore we get
\(\dfrac{\cos(x)\cdot(1-\sin(x))}{\cos^2(x)}\)Simplify the fraction by a factor of cos(x)
\(\dfrac{1-\sin(x)}{\cos(x)}\)Break up the fraction as a sum of fractions
\(\dfrac{1}{\cos(x)}-\dfrac{\sin(x)}{\cos(x)}\)Knowing that
\(\begin{gathered} \tan(x)=\dfrac{\sin(x)}{\cos(x)}\text{ and} \\ \\ \sec(x)=\dfrac{1}{\cos(x)} \end{gathered}\)We get
\(\sec(x)-\tan(x)\)Therefore we say that the equality holds and the statement is true.
Work out the length of x.
Give your answer rounded to 1 decimal place.
x
9 m
14.5 m
The diagram is not drawn accurately.
Please help

Answers
Answer:
x ≈ 17.1 m
Step-by-step explanation:
Using Pythagoras' identity in the right triangle
x² = 9² + 14.5² = 81 + 210.25 = 291.25 ( take the square root of both sides )
x = \(\sqrt{291.25}\) ≈ 17.1 m ( to 1 dec. place )
Which value of x is a solution to this equation?
3x2 minus 30x minus 72 = 0
A
x = negative12
B
x = negative4
C
x = negative2
D
x = negative6
Answers
The solution to the equation 3x2 - 30x - 72 = 0 is x = -4 and x = -12.
3x2 - 30x - 72 = 0
3x2 - 30x = 72
3x2 - 24x = 90
3x2 - 24x + 18x = 90 + 18x
3x(x - 8) = 108
x(x - 8) = 36
x = 36 or x = 8
x = -12 or x = -4
The equation 3x2 - 30x - 72 = 0is a second-degree polynomial equation with two solutions. To solve this equation, first use the distributive property to factor out 3x from the first two terms. This yields 3x(x - 8) = 108. Then divide both sides of the equation by 3 to get x(x - 8) = 36. From here, use the quadratic formula to solve for x. This yields x = 36 or x = 8. Since the equation was given in terms of x2, the two solutions are x = -12 and x = -4. To confirm this, substitute these values into the original equation and check that it is true.
Learn more about equation here
https://brainly.com/question/29657992
#SPJ4
if the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other. a) true b) false
Answers
The statement "if the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other" is true. The dot product of two vectors is zero if and only if the vectors are perpendicular.
The dot product of two vectors is defined as the product of their magnitudes and the cosine of the angle between them. When the dot product is zero, it means that the cosine of the angle between the vectors is zero, which occurs when the vectors are perpendicular.
In other words, the dot product being zero indicates that the vectors are at a 90-degree angle to each other, supporting the statement that they are perpendicular.
Learn more about dot product here: brainly.com/question/23477017
#SPJ11
f(x) = x³ - 3x
Find f(-2)
Answers
Answer:
To find f(-2), we substitute -2 for x in the expression for f(x) and simplify:
f(x) = x³ - 3x
f(-2) = (-2)³ - 3(-2)
f(-2) = -8 + 6
f(-2) = -2
Therefore, f(-2) = -2.
Step-by-step explanation:
2023
In a coin box there are 20-cent, 50-cent and $1 coins. The number of 20-cent coins is 2x, the number of 50-cent coins is y and the number of $1 coins is 4x. If the total value of the coins is $58.80, what is the total number of coins?
Answers
13 coins (50 cent)
24 coins (20 cent)
Let H = {0, ±3, ±6, ±9, . . .}. Find all the left cosets of H in Z.
Answers
There are three left cosets of H in Z, given by:
H = {3k | k ∈ Z}
[1] + H = {3k + 1 | k ∈ Z}
[2] + H = {3k + 2 | k ∈ Z}
To find all the left cosets of H in Z, we need to find the equivalence classes of the relation x ~ y if and only if x - y ∈ H. That is, two integers are equivalent if their difference is a multiple of 3.
To find the left cosets, we choose a representative for each equivalence class. We can choose any integer in the class as the representative. Then, we add H to the representative to obtain the left coset.
For example, the equivalence class [0] consists of all integers that are multiples of 3. We can choose 0 as the representative. Then, the left coset is
[0] + H = {0 + 3k | k ∈ Z} = {3k | k ∈ Z}
Similarly, we can choose 1, 2 as the representatives for [1], [2], respectively, and obtain the left cosets:
[1] + H = {1 + 3k | k ∈ Z} = {3k + 1 | k ∈ Z}
[2] + H = {2 + 3k | k ∈ Z} = {3k + 2 | k ∈ Z}
We can continue this process to find all the left cosets. In general, there are three left cosets of H in Z, given by:
H = {3k | k ∈ Z}
[1] + H = {3k + 1 | k ∈ Z}
[2] + H = {3k + 2 | k ∈ Z}
Learn more about cosets here:
https://brainly.com/question/32093909
#SPJ11
Factor the greatest common factor. 5xy4-20x2y3
Answers
Answer:
Step-by-step explanation:
The greatest common factor of 5 and -20 is 5
x: the greatest common factor is x
y: the greatest common factor is y^3
Answer: 5xy^3(y - 4x)
This table shows the linear relationship of the number of movies rented from a video store and total cost. enter the rate of change of this function
Answers
Step 1:
The rate of change of this function.
Step 2:
What is the slope of the linear relationship?
Step 3:
Learn more about the rate of change of a linear function. In the context of the given table showing the linear relationship between the number of movies rented from a video store and the total cost, the rate of change represents the slope of the function. It indicates how the total cost changes for each additional movie rented. The rate of change, or slope, can be calculated by dividing the change in the total cost by the change in the number of movies rented. It provides valuable information about the constant increase or decrease in cost per movie. A positive slope indicates an increasing cost, while a negative slope represents a decreasing cost. Understanding the rate of change helps to analyze the relationship between variables and make predictions about future costs based on the number of movies rented.
#SPJ11
The change in total cost by the change in the number of movies rented, we can find the rate at which the total cost changes per movie rented.
What units would the rate of change be expressed in?The rate of change of the linear function representing the number of movies rented from a video store and the total cost can be determined by examining the slope of the line connecting the data points.
The slope represents the rate at which the total cost changes for each additional movie rented.
To calculate the rate of change, we can select any two data points from the table and use the formula: rate of change = (change in total cost) / (change in number of movies rented).
By dividing the change in total cost by the change in the number of movies rented, we can find the rate at which the total cost changes per movie rented.
Learn more about rate
brainly.com/question/30548043
#SPJ11
Please help this is due in 44 minutes!

Answers
Answer:
it is A
Step-by-step explanation:
Plz, Solveeeeeeeeeeeeeeeeeeee! I will give you all my points

Answers
1/2b4 = 18
b4= 36
b= 9 yards