Solve for the dimensions of the area model below and then write an equation showing how the area as a sum is equivalent to the area as a product.
Answers
Full question:
For each multiplication expression, sketch an area model. Label the dimensions and the area of each part. Then write an equation showing that the area as a product equals the area as a sum. a. (x+1)(x+2), b. 3(2x+5), c. (2x-3)(x+2), d. (x-1)(y-1), e. -2y(y+3), f. (-x+1)(3x+y-4)
Answer and explanation:
a. (x+1)(x+2)= x×x+x×2+1×x+1×2
The dimensions (length and width) is x+1 and x+2
b. 3(2x+5) = 3×2x+3×5
The dimensions is 3 and 2x+5
c. (2x-3)(x+2)= 2x×x+2x×2-3×x-3×+2
The dimensions are 2x-3 and x+2
d. (x-1)(y-1)= x×y+x×-1-1×y-1×-1
Dimensions are x-1 and y-1
e. -2y(y+3)= -2y×y-2y×3
Dimensions are -2y and y+3
f. (-x+1)(3x+y-4)= -x×3x-x×y-x×-4+1×3x+1×y+1×-4
Dimensions are -x+1 and 3x+y-4
Related Questions
Please help please I really need help

Answers
Answer:
C. No, because 10² + 24² ≠ 34²
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightTrigonometry
[Right Triangles Only] Pythagorean Theorem: a² + b² = c²
a is a leg b is another leg c is the hypotenuseStep-by-step explanation:
Step 1: Define
Identify variables
a = 24
b = 10
c = 34
Step 2: Check
Verify ΔLMN is a right triangle
Substitute in variables [Pythagorean Theorem]: 24² + 10² = 34²Evaluate exponents: 576 + 100 = 1156Add: 676 ≠ 1156∴ ΔLMN is not a right triangle
HELP PLEASE!! ASAP!! no links please

Answers
Answer:
1st. 1/4
2nd. Not proportional
Step-by-step explanation:
Answer:
both are not proportional
Step-by-step explanation:
16 : 4 = 16/4 = 4
20 : 5 = 20/5 = 4
9 : 36 = 9/36 = 1/4
not the same so NOT proportional
4 : 12 = 4/12 = 1/3
5 : 20 = 5/20 = 1/4
9 : 45 = 9/45 = 1/5
not the same so NOT proportional
Subtract. (− 3 f + 9) − (9 − 3 f)
Answers
Answer:
Step-by-step explanation:\
first open the brackets
-3f + 9 - 9 -3f
collect like terms
-3f -3f +9 -9
-6f + 0
here you go :)
-3f + 3f +9 -9
0
Bryant Industries uses forecasting to estimate the number of orders that will be placed by their customers. The table below gives the sales figures for the last four months. Month 2 3 4 5 Sales 924 91
Answers
Bryant Industries uses forecasting to estimate the number of orders that will be placed by their customers. The table below gives the sales figures for the last four months.Month2345Sales92491942004There are different forecasting techniques used by companies like Bryant Industries to predict future sales.
One of the most widely used methods is the time-series method. This method is particularly useful when the demand for a product or service changes over time and when there are no external factors that affect the sales. In this case, we can use a time-series method called the moving average to estimate future sales. The moving average is a time-series method that uses the average of past sales data to estimate future sales. It is particularly useful when there are no external factors that affect the sales. In this case, we can use a 3-month moving average to estimate future sales. The 3-month moving average is calculated as follows: (924 + 919 + 420) / 3 = 754.33. This means that we can expect sales of around 754 units next month. The moving average method is easy to use and is a good way to get a quick estimate of future sales. However, it has some limitations. For example, it does not take into account external factors that may affect sales, such as changes in the economy or in consumer behavior.
In conclusion, Bryant Industries can use the moving average method to estimate future sales. However, they should also consider other factors that may affect sales, such as changes in the economy or in consumer behavior. By doing so, they can make more accurate forecasts and improve their overall performance.
To learn more about time-series method visit:
brainly.com/question/32443421
#SPJ11
Which triangles are similar?
A. Triangles A and B
B. Triangles A, B, and C
C. Triangles A and C
D. Triangles B and C

Answers
Answer:
D. Triangles B and C
Step-by-step explanation:
When we look to Triangles B & C :-
37° = 37°
53° = 53°
90° = 90°
Therefore, both Triangles B and C are similar.
Answer:
D. Triangles B and C
Step-by-step explanation:
Which value of the variable is the solution of the equation?
a + $5.92 = $12.29 a = $5.37, $5.47, $6.37, $6.27
Answers

how do i solve this exponential equation

Answers
Answer:
x = 0 or 1/2
Step-by-step explanation:
Solving an exponential equation of this nature with different bases and coefficients is always a bit of an ad hoc affair. Here, we can divide by the right side expression and make a substitution that turns it into a quadratic.
__
\(3\cdot16^x+2\cdot81^x=5\cdot36^x\\\\0.6\left(\dfrac{4}{9}\right)^x+0.4\left(\dfrac{9}{4}\right)^x=1\\\\\textsf{Let $z=\left(\dfrac{4}{9}\right)^x$}\\\\0.6z+\dfrac{0.4}{z}=1\qquad\text{after substitution}\\\\3z^2-5z +2 = 0\qquad\text{multiply by $5z$ and put in standard form}\\\\(3z-2)(z-1)=0\qquad\text{factor}\\\\z=\dfrac{2}{3}\quad\text{or}\quad z=1\\\\x=\dfrac{\log(z)}{\log(4/9)}=\boxed{\dfrac{1}{2}\quad\text{or}\quad 0}\)
_____
Additional comment
A graphing calculator often solves these very nicely, especially when the equation is put into the form f(x) = 0.

Suppose J=[−2365].
What is the value of |J|?
Enter your answer in the box.
![Suppose J=[2365].What is the value of |J|?Enter your answer in the box.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/6oqjvrkTWdjVsxHMUCsSOxwRyLQZisRb.png)
Answers
Answer:
The determinant of J can be found using the formula ad - bc
where \(\left[\begin{array}{cc}a&b\\c&d\end{array}\right]\)
So we have \(-2 * 5 - 6 * 3 = -10 - 18 = -28\)
Step-by-step explanation:
The value of |J| is 28.
What is matrix?Matrix, a set of numbers arranged in rows and columns so as to form a rectangular array.
Given:
J=[−2365].
now, determinant of the matrix J is
|J|= |(-2) * 5 - 3*6|
|J|= |-10 - 18|
|J|= |-28|
|J|= 28
hence, the value of |J| is 28.
Learn more about matrix here:
https://brainly.com/question/4030813
#SPJ2
find the missing values
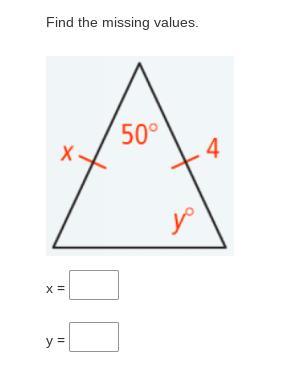
Answers
Answer:
y= 65
x=4
Step-by-step explanation:
What is the expected frequency of east campus and passed?
a) 50.5 students
b) 39 students
c) 42 students
d) 48.3 students
Answers
The expected frequency of east campus and passed is C. 42 students
How to calculate the value?The table for expected frequency is ,
East Campus West Campus Total
Passed (84*100)/22=42 (84*100)/200 =42 84
Failed (116*100)/200=58 (116*100)/22=58 116
Total 100 100 200
Passed = 84×100/200
= 42
Therefore, the expected frequency of East Campus and Passed is 42 students.
Learn more about frequency on:
https://brainly.com/question/254161
#SPJ4

mark pushes his broken car 130 m down the block to his friend's house. he has to exert a 120 n horizontal force to push the car at a constant speed.
Answers
The work done by Mark in pushing his broken car 130 meters down the block with a 120 N horizontal force is 15,600 J (joules).
We can use the formula: Force (F) = mass (m) x acceleration (a)
Since the car is not accelerating, the acceleration is 0 m/s^2. Therefore, we can solve for the mass of the car:
120 N = m x 0 m/s^2
m = 0 kg
This is not a realistic value for the mass of a car, but it means that the car is not affected by gravity or any other forces that would cause it to accelerate.
Now, we can calculate the work done by Mark on the car:
Work (W) = force (F) x distance (d)
W = 120 N x 130 m
W = 15,600 J
Therefore, Mark has exerted a total of 15,600 joules of work to push his broken car 130 meters down the block to his friend's house.
To determine the work done by Mark in pushing his broken car 130 meters to his friend's house, we can use the formula for work: Work = Force x Distance x cos(theta). In this case, the horizontal force exerted is 120 N, and the distance is 130 m. Since Mark is pushing the car horizontally, the angle between the force and the displacement is zero degrees. The cosine of zero degrees is 1. So, the work done is Work = 120 N x 130 m x 1.
To know more about horizontal visit :-
https://brainly.com/question/27860688
#SPJ11
COULD SOMEONE PLS HELP

Answers
Answer:
125
Step-by-step explanation:
Angles on a straight line =180
180- (35+20) =125
Reasoning= angles on a straight line add up to 180
so 180 - (35+20) = 135
on a roadway with eight 11 ft lanes (four in each direction), a horizontal curve is designed with a radius of 1176 ft, and a concrete wall is built at 70 ft from the center line, what is the sight distance for the driver?
Answers
The sight distance for the driver on the given road with the mentioned conditions is calculated to be approximately 860.8 ft.
To calculate the sight distance for the driver, we need to use the horizontal curve sight distance formula. The formula is:
SD = 2/3 × ((h + R)² / (2 × R - f))
Where:
SD = sight distance
h = height of driver's eye above the roadway surface (in feet)
R = radius of the curve (in feet)
f = distance from the driver's eye to the object or obstacle (in feet)
First, we need to determine the height of the driver's eye. A typical height for a driver's eye above the roadway surface is 3.5 feet. Therefore, we will assume that h = 3.5 ft.
Next, we need to determine f, which is the distance from the driver's eye to the concrete wall. Since the wall is located 70 feet from the center line of the roadway, we can determine f as follows:
f = (W / 2) + S
Where:
W = width of the roadway (in feet)
S = distance from the center line to the wall (in feet)
Substituting the given values, we get:
f = (8 × 11 / 2) + 70 = 114 ft
Now, we can plug in the values for h, R, and f into the sight distance formula:
SD = 2/3 × ((3.5 + 1176)² / (2 × 1176 - 114))
Simplifying the formula, we get:
SD ≈ 860.8 ft
Therefore, the sight distance for the driver on this roadway with a horizontal curve of radius 1176 ft and a concrete wall built at 70 ft from the center line is approximately 860.8 ft.
Learn more about Horizontal Curve :
https://brainly.com/question/29366319
#SPJ4
Alex knits hats and scarves to sell at a craft market. He can make at most 20 hats and 30 scarves, but no more than 40 items altogether, in time for the market.
Write and graph a system of inequalities that shows the possible numbers of hats and scarves Alex can bring to the craft market if he wants to bring at least 25 items. Identify three (3) possible combinations, and say which he should
choose.
Answers
The three (3) possible combinations are
hats = 10, scarves = 30hats = 10, scarves = 20hats = 20, scarves = 20Alex should 20 hats and 20 scarves
How to find the possible combinations Alex can bring to the marketLet the number of scarves be x and y be the number of hats
He can make at most 20 hats and 30 scarves, but no more than 40 items altogether
x ≤ 20
y ≤ 30
x + y ≤ 40 (in time of market)
x + y ≥ 25
The possible combinations are
1 ⇒ x = 10, y = 302 ⇒ x = 10, y = 203 ⇒ x = 20, y = 20He should choose the third option x = 20, y = 20 this allows him to take more products to the show
Learn more about inequality graph at:
https://brainly.com/question/11234618
#SPJ1

If X has the hypergeometric distribution, what is the minimum value that X can take?
N – K
N
K
n
0
Answers
If X has the hypergeometric distribution, the minimum value that X can take is option (e) 0
The hypergeometric distribution models the probability of getting a certain number of successes in a fixed-size sample drawn without replacement from a finite population containing a known number of successes and failures.
The minimum value that X can take depends on the specific parameters of the distribution.
If the population size is N, the number of successes in the population is K, and the sample size is n, then the minimum value that X can take is max(0, n - (N - K)).
This is because the sample can contain at most n items, and if all of them are failures (i.e., none of them are successes), then X would be 0. On the other hand, if there are fewer than n failures in the population, then the sample can contain at most n - (N - K) successes. If n - (N - K) is negative, then there are more successes than failures in the population, and X can take any value between 0 and n, inclusive.
Therefore, the correct option is (e) 0
Learn more about hypergeometric distribution here
brainly.com/question/30911049
#SPJ4
5. Which of the following rational numbers does not lie between (2/5 and 3/4
Answers
From the given options, the rational number that does not lie between 2/5 and 3/4 is option (d) 9/20.
We need to discover a number that is either smaller than 2/5 or greater than 3/4 in order to find a rational number that does not fall between these two numbers.
Let's contrast each choice with the range provided:
a. 17/20 does not fall between 2/5 and 3/4 because it is more than 3/4.
b. 13/20: This number falls inside the provided range and is not the solution we are seeking for because it is larger than 2/5 but smaller than 3/4.
c. 11/20: This number falls inside the provided range and is not the solution we are seeking for because it is larger than 2/5 but smaller than 3/4.
d. 9/20: Because this number is less than 2/5, it does not fall within the range.
From the given options, the rational number that does not lie between 2/5 and 3/4 is option (d) 9/20.
Learn more about rational number click;
https://brainly.com/question/17450097
#SPJ1
Complete question =
Choose a rational number which does not lie between 2/5 and3/4.
a.17/20
b.13/20
c.11/20
d.9/20
3. If A = 49° and a = 10, find c.
Answers
The triangle is solved using the law of sines and c = 13.25
Given data ,
Let the triangle be represented as ΔABC
Now , the measure of sides of the triangle are
The measure of ∠BAC = 49°
The measure of ∠ACB = 90°
And , the measure of side a = 10 units
From the law of sines ,
a / sin A = b / sin B = c / sin C
10 / sin 49° = c / sin 90°
The triangle is solved using the law of sines , where the measure of sine of angle opposite to the sides are in the same ratio.
The trigonometric value of sin 90° = 1
c = 10 / 0.75470958022
c = 13.25 units
Therefore , the measure of c = 13.25 units
Hence , the triangle is solved and c = 13.25 units
To learn more about law of sines click :
https://brainly.com/question/13098194
#SPJ1
The complete question is attached below :
If A = 49° and a = 10, find c.

in how many ways can eight different books be distributed to 12 children if no child more than one book
Answers
The number of ways to distribute the books is calculated using the concept of permutations, specifically the concept of selecting a subset without replacement. The answer is 199,584 possible ways.
In this scenario, we have 12 children and 8 different books. Since each child can receive at most one book, we can view this problem as selecting a subset of 8 books from the total set of 12 children.
To calculate the number of ways to distribute the books, we use the concept of permutations. Specifically, we use the formula for selecting a subset without replacement, denoted as nPr, where n is the total number of children and r is the number of books to be distributed.
Using this formula, we calculate 12P8, which is equivalent to 12!/(12-8)!. Simplifying this expression, we have 12!/4!. Evaluating the factorials, we find 12! = 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 and 4! = 4 × 3 × 2 × 1.
By dividing 12! by 4!, we obtain 199,584, which represents the number of ways to distribute the 8 different books to the 12 children, ensuring that each child receives at most one book.
In summary, there are 199,584 possible ways to distribute the eight different books among 12 children, with each child receiving at most one book. This is calculated using the concept of permutations, specifically the formula 12P8 = 12!/4!.
Learn more about permutations here:
https://brainly.com/question/29990226
#SPJ11
Study the information provided below and answer the questions that follow. Chief executive officers (CEOs) have long been a focus of organisational research. This emphasis is understandable, given the widespread belief that a firm's top executive has a substantial impact on its performance. Three years ago, the board of directors (BOD) of TMG Ltd and the then incumbent CEO mutually agreed to part ways due to poor financial performance of the business. The new CEO appointed to replace him was mandated by the BOD to initiate an intervention strategy to turn around the business. As part of a review of the financial performance of the business, a researcher has recently been contracted by the BOD of TMG Ltd to determine whether the intervention strategy introduced three years ago by the current CEO has produced significantly improved outcomes for the business. The BOD wants the quarterly operating profit margin of the business for the past six year to constitute the unit of analysis. Table 4.1, below, shows the quarterly operating profit margin retrieved from the database of the company. Table 4.1: Quarterly operating profit margin (%) of TMG Ltd over the past six years.
Answers
The quarterly operating profit margin of TMG Ltd over the past six years is provided in Table 4.1, indicating the financial performance of the business during that period.
In order to assess the impact of the intervention strategy introduced by the current CEO three years ago, the board of directors (BOD) of TMG Ltd has contracted a researcher to analyze the data and determine if there have been significant improvements in the business outcomes. The quarterly operating profit margin serves as the unit of analysis for this evaluation.
Table 4.1 allows the researcher to examine the trend and fluctuations in the quarterly operating profit margin over the six-year period. By analyzing the data, the researcher can identify any noticeable changes in the financial performance of TMG Ltd, particularly after the implementation of the intervention strategy. The BOD is interested in understanding whether the strategy has resulted in improved profitability and overall financial health of the company.
The researcher will likely perform statistical analysis, such as calculating averages, trends, and identifying any significant variations, to draw conclusions about the effectiveness of the intervention strategy. By comparing the quarterly operating profit margin before and after the strategy's implementation, the researcher can assess whether the new CEO's efforts have had a positive impact on the company's financial performance.
Learn more about financial performance here: brainly.com/question/28287663
#SPJ11
Input Output
94 99
85
16 21
75 80
62 67
what is the answer
of this function machine
Answers
Answer:
Rule is add 5
Step-by-step explanation:
Therefore, 85 is the input and 90 is the output
the length of a rectangle is six inches more than eight times the width. the perimeter is 120 inches. find the length and width.
Answers
The length and width of a rectangle are 36cm and 4.5cm
Finding the Width:
The formula to find the perimeter of the rectangle is:
P=2(l+w),
where P is the perimeter, l be the length, and w be the width.
Now substitute the given values to solve for w, since we need to find the width.
The given information is:
the length of a rectangle is six inches more than eight times the width so the equation becomes:
L=8w+6
P=120
w=8w
now plug the values in the above formula:
P=2(l+w),
120=2(8w+6)+8w
120=16w+12+8w
120=24w+12
24w=108
w=4.5
To find the length just substitute in the L.
L=8(4.5)+6
L=30+6
L=36
To know more about the Perimeter of a rectangle:
https://brainly.com/question/24571594
#SPJ4
find the slope of the following ^ :))
|

Answers
Answer:
m [slope] = 0
Step-by-step explanation:
When the slope is 0, x cancels out so the y value will remain the same.
There are several methods to finding slope but the easiest way to do this is by dividing the second y value - first y value by the second x value - first x value.
m = ∆y/∆x = y2-y1/x2-x1
You y2 and x2 are interchangable with y and x, because y1, and x1 are part of the starting coordinate,.
The reason you subtract the second
value from the first is because in a directly proportional relationship, y increases as x increases so the next x values will have a greater y value, this is a measure of steepness.
So the slope is:
-1 - -1 / 3 - -2 = -1 + 1 / 3 + 2 = 0 / 5 = 0.
Answer:
heres what u need
Step-by-step explanation:
\(\frac{-1}{-2} \frac{-1}{3}\)
divide top from bottom
\(-2/-1=2\)
2 is your x
\(3/-1=-3\)
-3 is your y
so your slope is (2,-3)
simplify this problem\( \frac{9x}{4x - 4} + \frac{ {x}^{2} + 6x }{ {x}^{2} + 5x - 6} \)
Answers
1. Factor the denominators as follow:
\(\begin{gathered} 4x-4=4(x-1) \\ \\ \\ x^2+5x-6 \\ =x^2+6x-x-6 \\ =x(x+6)-(x+6) \\ =(x-1)(x+6) \\ \\ \\ \\ \\ \frac{9x}{4(x-1)}+\frac{x^2-6x}{(x-1)(x+6)} \end{gathered}\)2. Write the expresion with the less common denominator:
Multiply the first fraction by (x+6) (both parts, numerator and denominator):
\(\frac{9x}{4(x-1)}\cdot\frac{x+6}{x+6}=\frac{9x(x+6)}{4(x-1)(x+6)}\)Multiply the second fraction by 4 (both parts, numerator and denominator):
\(\frac{x^2-6x}{(x-1)(x+6)}\cdot\frac{4}{4}=\frac{4(x^2-6x)}{4(x-1)(x+6)}\)Rewrite the expression with the less common denominator:
\(\begin{gathered} \frac{9x(x+6)}{4(x-1)(x+6)}+\frac{4(x^2-6x)}{4(x-1)(x+6)} \\ \\ =\frac{9x(x+6)+4(x^2-6x)}{4(x-1)(x+6)} \end{gathered}\)3. Remove parentheses and simplify:
\(\begin{gathered} \frac{9x^2^{}+54x+4x^2-24x}{(4x-4)(x+6)} \\ \\ =\frac{13x^2+30x}{4x^2+24x-4x-24} \\ \\ =\frac{13x^2+30x}{4x^2+20x-24} \end{gathered}\)Then, the given expression simplified is:\(\frac{9x}{4x-4}+\frac{x^2-6x}{x^2+5x-6}=\frac{13x^2+30x}{4x^2+20x-24}\)![simplify this problem[tex] \frac{9x}{4x - 4} + \frac{ {x}^{2} + 6x }{ {x}^{2} + 5x - 6} [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/3FEf63pRqLXeuugCPzvxJcejYts4in3X.png)
The next two questions involve predicting the height of a population of girls at age 18 based on each girls height at age 2. We have a sample of 70 girls from Berkley, CA born in 1928-1929 where we have measured their height at age 2 and 18. Let +=the height of girls at age 2 in cm's .y = the height of girls at age 18 in cm's. The the following are the appropriate summary statistics n = 70 = 87.25, y = 166.54, R = 0.664. S 3.33. 6.07 Dscat_girls.
Answers
The regression equation for predicting the height of girls at age 18 based on their height at age 2 is:
y ≈ 68.953 + 1.210x
What is linear regression?The correlation coefficient illustrates how closely two variables are related to one another. This coefficient's range is from -1 to +1. This coefficient demonstrates the degree to which the observed data for two variables are significantly associated.
Based on the given information, we can use the linear regression model to predict the height of girls at age 18 based on their height at age 2. Here are the summary statistics:
n = 70 (sample size)
x = 87.25 (mean height at age 2 in cm)
y = 166.54 (mean height at age 18 in cm)
R = 0.664 (correlation coefficient)
S = 3.33 (standard deviation of height at age 2 in cm)
\(S_y\) = 6.07 (standard deviation of height at age 18 in cm)
To predict the height of girls at age 18 (y) based on their height at age 2 (x), we can use the regression equation:
y = a + bx
where a is the y-intercept (predicted height at age 18 when x = 0) and b is the slope of the regression line.
From the given information, we have the following values:
x = 87.25
y = 166.54
R = 0.664
Using these values, we can calculate the slope (b) of the regression line:
b = R * (\(S_y\) / S)
= 0.664 * (6.07 / 3.33)
≈ 1.210
Next, we can calculate the y-intercept (a) using the formula:
a = y - b * x
= 166.54 - 1.210 * 87.25
≈ 68.953
Therefore, the regression equation for predicting the height of girls at age 18 based on their height at age 2 is:
y ≈ 68.953 + 1.210x
Learn more about linear regression on:
https://brainly.com/question/27426965
#SPJ4
Mrs. Anderson bought $17.01 worth of ribs (r) and chicken (c). Ribs cost $1.89 per pound and chicken costs $0.90 per pound.
Write the equation that would represent this situation.
Pls hurry‼️‼️
Answers
r = ribs
c= chicken
Answer:
Step-by-step explanation:
17.01 = 1.89(r) + 0.90(c)
Monica’s school band held a car wash to raise money for a trip to a parade in New York City. After washing 125 cars, they made $775 from a combination of $5. 00 quick washes and $8. 00 premium washes. Let x represent the number of quick washes and let y represent the number of premium washes. Which system of linear equations represents the situation? 5x 8y = 775 and x y =125 5x – 8y = 125 and x y = 775 5x 8y = 775 and x – y = 125 5x – 8y = 125 and x – y = 775.
Answers
The system of linear equations that represents the situation is: 5x - 8y = 775 and x + y = 125.
How can we express the situation using linear equations?The given situation involves Monica's school band organizing a car wash to raise money for a trip to a parade in New York City. They washed a total of 125 cars and made $775 from a combination of $5.00 quick washes and $8.00 premium washes.
To represent this situation using a system of linear equations, we need to assign variables to the number of quick washes (x) and the number of premium washes (y).
First, we can express the total amount earned from the car washes. Since each quick wash earns $5.00 and each premium wash earns $8.00, the equation becomes:
5x + 8y = 775.
Next, we consider the total number of cars washed. Since the band washed a total of 125 cars, we can write the equation as:
x + y = 125.
Therefore, the system of linear equations that represents the situation is:
5x - 8y = 775
x + y = 125.
By solving this system of equations, we can find the values of x and y, which will provide the number of quick washes and premium washes respectively.
Learn more about linear equations
brainly.com/question/12974594
#SPJ11
i need an expression for d and how far the star is from the sun

Answers
Step 1
Find the distance between the sun and the star using SohCahToa.
For this problem we use Toa.
\(\text{Tan}\theta=\frac{\text{opposite}}{\text{adjacent}}\)
where;
\(\begin{gathered} \theta=0.00001389^o \\ \text{adjacent}=\text{ d} \\ \text{Opposite}=\text{ 1 AU} \end{gathered}\)Step 2
Substitute and find the value of d
\(\begin{gathered} \text{Tan}0.00001389=\frac{1}{d} \\ d=\frac{1}{Tan0.00001389} \\ \end{gathered}\)\(d\text{ = 4}124966.128\text{ AU}\)
can the tangent constraint be applied between a line and an arc?
Answers
Yes, the tangent constraint can be applied between a line and an arc in many CAD (Computer-Aided Design) software programs.
In CAD, a tangent constraint is a geometric constraint that forces two entities (lines, arcs, circles, etc.) to share a common tangent at their point of contact. When you apply a tangent constraint between a line and an arc, the software will ensure that the line and the arc are always tangent to each other at their point of intersection.
This constraint is useful for designing mechanical components, such as gears or cams, where you need to ensure that the contact between two parts is smooth and continuous. It is also commonly used in architecture, where a building's curved surfaces may need to be tangent to adjacent straight lines or walls.
In short, the tangent constraint can be applied between a line and an arc, and it is a useful tool in many different fields of design.
Learn more about geometric constraint here
brainly.com/question/30319646
#SPJ4
STRUCTURE Find the slope of the line that passes through the pair of points.
ty
O
(0, 1)
(1,-2)
X
Answers
The slope of the line that passes through the pair of points (0, 1) and (1, -2) will be -3.
First, let us understand the slope of a line:
A slope of a line is defined in mathematics as the change in the y coordinate with regard to the change in the x coordinate.
We are given the points:
(0, 1) and (1, -2)
We will calculate the slope of the line using the following formula:
m = (y_2 - y_1) / (x_2 - x_1)
Let x_1 = 0, x_2 = 1, y_1 = 1 and y_2 = -2.
Substitute the given values in the above formula, we will get:
m = (-2 - 1) / (1 - 0) = -3 / 1 = -3
So, the slope of the line is -3.
Thus, the slope of the line that passes through the pair of points (0, 1) and (1, -2) will be -3.
To learn more about the slope of a line visit:
https://brainly.com/question/16180119
#SPJ1
use the formula for finding surface area of rectangular prism
A =PH +2B Solve for P
Answers
Answer:
P=(A-2B)/H
Step-by-step explanation:
A=PH+2B
takeaway 2b from both sides
A-2b=ph
divide both sides by h
(A-2B)/H=P