Simplify the expression using properties of exponents. 10a-8b-2/4a3b5
Answers
=52a−11b−7
Explanation:
10
a
−
8
b
−
2
4
a
3
b
5
Note:
a
m
a
n
=
a
m
−
n
Applying the above property to the exponents of
a
and
b
=
(
10
4
)
.
a
(
−
8
−
3
)
.
b
(
−
2
−
5
)
=
5
2
a
−
11
b
−
7
Related Questions
2. The diagram above shows a wooden structure in the form of a cone mounted on hemispherical base. The vertical height of the cone is 24cm and the base 7cm. Calculate correct to 3 significant figures the surface area of the structure. (Take π= 22/7)
Answers
The surface area of the wooden structure is approximately 1012 cm².
To calculate the surface area of the wooden structure, we need to find the surface area of the cone and the surface area of the hemispherical base, and then add them together.
Surface Area of the Cone:
The surface area of a cone is given by the formula:
A_{cone = \(\pi \times r_{cone} \times (r_{cone} + s_{cone})\), \(r_{cone\) is the radius of the base of the cone and \(s_{cone\) is the slant height of the cone.
The vertical height of the cone is 24 cm, and the base radius is 7 cm, we can calculate the slant height using the Pythagorean theorem:
\(s_{cone\) = \(\sqrt{(r_{cone}^2 + h_{cone}^2).\)
Using the given measurements:
\(s_{cone\) = √(7² + 24²) cm
\(s_{cone\) ≈ √(49 + 576) cm
\(s_{cone\) ≈ √625 cm
\(s_{cone\) ≈ 25 cm
Now, we can calculate the surface area of the cone:
\(A_{cone\) = π × 7 cm × (7 cm + 25 cm)
\(A_{cone\) = (22/7) × 7 cm × 32 cm
\(A_{cone\) = 704 cm²
Surface Area of the Hemispherical Base:
The surface area of a hemisphere is given by the formula:
\(A_{hemisphere\) = \(2 \times \pi \times r_{base}^2\), \(r_{base\) is the radius of the base of the hemisphere.
Given that the base radius is 7 cm, we can calculate the surface area of the hemispherical base:
\(A_{hemisphere\) = 2 × (22/7) × (7 cm)²
\(A_{hemisphere\) = (22/7) × 2 × 49 cm²
\(A_{hemisphere\) = 308 cm²
Total Surface Area:
To calculate the total surface area, we add the surface area of the cone and the surface area of the hemispherical base:
Total Surface Area = \(A_{cone} + A_{hemisphere}\)
Total Surface Area = 704 cm² + 308 cm²
Total Surface Area = 1012 cm²
For similar questions on surface area
https://brainly.com/question/16519513
#SPJ8
which of the binomials below is a factor of this trinomial
x^2-13x+30
Answers
The binomials (x - 3) and (x - 10) are factors of the trinomial x² - 13x + 30.
To determine which binomial is a factor of the trinomial x² - 13x + 30, we need to factorize the trinomial completely.
In this case, we need to find two binomials in the form (x - a)(x - b) that satisfy the equation:
(x - a)(x - b) = x² - 13x + 30
So, (x - 3)(x - 10) = x² - 13x + 30.
Therefore, the binomials (x - 3) and (x - 10) are factors of the trinomial x² - 13x + 30.
Learn more about Binomial here:
https://brainly.com/question/30339327
#SPJ1
I need help please I can only find 2 of these solutions

Answers
Step 1: Isolate the Sin Operator
\(8 sin(\frac{\pi }{6} x)=2\\sin(\frac{\pi }{6} x)=0.25\\\\\)
Step 2: Use Inverse Sin(arcsin) to isolate the term with the x variable
Note that since trig functions have 2 general solutions, this will give us one of our general solutions.
\(x=\frac{6 arcsin(0.25)}{\pi } =0.48\)
x₁= 0.48
Solving for x₂
Use the period identity for Sin Functions
\(sin(x)=sin(\pi -x)\)
X in this case is arcsin(0.25)
\(\frac{\pi }{6} x=\pi -arcsin(0.25) = 5.52\)
So our two general solutions are 0.48 and 5.52
Step 3: Period
Trig Functions have periodic behavior and this function period is
\(\frac{2\pi }{1} (\frac{6}{\pi } )= 12\)
So our general solutions are
0.48±12k, where k is an integer
5.52±12k, where k is an integer
Let k=1, and we get our next set of solutions:
12.48 and 17.52
So our answer is 0.48,5.52,12.48,17.52
Fill in the blank with the correct answer choice. A ___________ has exactly one pair of parallel lines. a. square c. trapezoid b. parallelogram d. rectangle Please select the best answer from the choices provided A B C D
Answers
Answer: C
Step-by-step explanation:
The rest of the quadrilaterals provided have 2 pairs of parallel lines.
The choice is:
CExplanation:
The quadrilateral that has exactly one pair of parallel lines is called a trapezoid.
Here's what a trapezoid looks like :
\(\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\linethickness{0.3mm}\qbezier(0,0)(0,0)(1,3)\qbezier(5,0)(5,0)(4,3)\qbezier(1,3)(1,3)(4,3)\qbezier(3,0)(8.2,0)(0,0)\put(-0.5,-0.3){$\sf A$}\put(5.3,-0.3){$\sf B$}\put(4.2,3.1){$\sf C$}\put(0.6,3.1){$\sf D$}\end{picture}\)
Hence, this makes C the correct choice.6) 1,1,3,8,19, 41
a) 60
b) 81
c) 90
d) 101
Analogias
Answers
The next term in the sequence is 98. None of the given options (60, 81, 90, 101) match the expected next term. None of the option is correct.
To find the pattern in the sequence 1, 1, 3, 8, 19, 41, we can examine the differences between consecutive terms:
1 1 3 8 19 41
0 2 5 11 22
Looking at the differences, we can observe that each subsequent difference is obtained by adding consecutive odd numbers: 2, 3, 4, 5, etc. This suggests that the original sequence may be related to square numbers.
Let's check if the differences between consecutive terms are square numbers:
2 = 1²
5 = 2² + 1²
11 = 3² + 2²
22 = 4² + 3²
Based on this pattern, we can make a reasonable assumption that the next difference should be 5² + 4² = 41 + 16 = 57. Adding this difference to the last term of the sequence (41), we get the next term:
41 + 57 = 98
Therefore, the next term in the sequence is 98. None of the given options (60, 81, 90, 101) match the expected next term.
Hence, none of the given options accurately continue the pattern of the sequence. It's important to note that patterns in sequences can sometimes have multiple possible interpretations, and it's always essential to consider alternative patterns or extend the sequence further to confirm the pattern.
For moresuch questions on sequence visit:
https://brainly.com/question/30762797
#SPJ8
For any positive integer n, the value of n! is the product of the first n positive integers. For example, 4! = 4 * 3 * 2 * 1 =24. What is the greatest common divisor of 5! and 7! ?
Answers
The GCD of 5! and 7! is 2^3 * 3^1 * 5^1 = 120.
the greatest common divisor of 5! and 7! is 120.
To find the greatest common divisor (GCD) of 5! and 7!, we need to factorize both numbers and identify the common factors.
First, let's calculate the values of 5! and 7!:
5! = 5 * 4 * 3 * 2 * 1 = 120
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5,040
Now, let's factorize both numbers:
Factorizing 120:
120 = 2^3 * 3 * 5
Factorizing 5,040:
5,040 = 2^4 * 3^2 * 5 * 7
To find the GCD, we need to consider the common factors raised to the lowest power. In this case, the common factors are 2, 3, and 5. The lowest power for 2 is 3 (from 120), the lowest power for 3 is 1 (from 120), and the lowest power for 5 is 1 (from both numbers).
For more such question on greatest common divisor
https://brainly.com/question/219464
#SPJ8
List the following numbers from greatest to least: -5, 4, 0, |-3|, -6, 2
6th grade integers
Answers
Answer:
4, 2, |-3|, 0, -5, -6
Step-by-step explanation:
5) Use the figure to answer the
following question.
Which expression can be used to find the volume of the figure below?
2 cm
Choose 1 answer:
A
B
8 cm
7 cm 1 cm
6 cm
cm x 7 cm x 1 cm) + (1 cm x 6 cm x 8 cm)
cm x 8 cm x 7 cm) + (1 cm x 6 cm x 8 cm)
cm x 7 cm) + (8 cm x 6 cm)
Option A above
O Option B above
O Option C above
*
1 point

Answers
An expression that can be used to find the volume of the figure include the following: B. (2 cm × 8 cm × 7 cm) + (1 cm × 6 cm × 8 cm).
How to calculate the volume of a rectangular prism?In Mathematics and Geometry, the volume of a rectangular prism can be calculated by using the following formula:
Volume of a rectangular prism = L × W × H
Where:
L represents the length of a rectangular prism.W represents the width of a rectangular prism.H represents the height of a rectangular prism.By substituting the given dimensions (parameters) into the formula for the volume of a rectangular prism, we have the following;
Volume of figure = (2 cm × 8 cm × 7 cm) + (1 cm × 6 cm × 8 cm)
Volume of figure = 112 cm³ + 48 cm³
Volume of figure = 160 cm³
Read more on volume of prism here: brainly.com/question/21012007
#SPJ1
N
m
4
5
4
U
-
3-
Cu v
-5-4-3-2-1
2
-2
1 w
60
r
2345x
What is the domain of the function on the graph?
O all real numbers
O all real numbers greater than or equal to-2
O all real numbers greater than or equal to-5
O all real numbers greater than or equal to 0
Help please

Answers
Answer:
Step-by-step explanation:
Question
N
m
4
5
4
U
-
3-
Cu v
-5-4-3-2-1
2
-2
1 w
60
r
2345x
What is the domain of the function on the graph?
O all real numbers
O all real numbers greater than or equal to-2
O all real numbers greater than or equal to-5
O all real numbers greater than or equal to 0
Help please
Let f(x)=x^3-6x+3 i. find the domain of the function and f’(x) in the domain.
Answers
Domain of a any cubic function \(f(x)=ax^3+bx^2+cx+d\) is defined to be always \(\mathbb{R}\).
The derivative with respect to x of your cubic function is,
\(\dfrac{d}{dx}f(x)=f'(x)\)
to find the derivative of a polynomial function, simply take a derivative of each factor and sum them up,
\(\dfrac{d}{dx}x^3=3x^2\) by the rule \(\dfrac{d}{dx}x^m=mx^{m-1}\) where \(m\in\mathbb{R}\)
\(\dfrac{d}{dx}-6x=-6\)
\(\dfrac{d}{dx}3=0\)
So the derivative is,
\(f'(x)=3x^2-6\)
both derivative and the original function have equal domain.
Hope this helps :)
Step-by-step explanation:
\(thank \: you\)

The values in the table represent the graph of a continuous function. Which interval must contain an x-intercept? x y –3.1 –1.85 –2.7 –0.84 –2.3 –0.09 –1.9 0.44 –1.5 0.79 –1.1 1.00 –0.7 1.10 –0.3 1.13 0.1 1.13 –3.1 < x < –2.7 –2.3 < x < –1.9 –1.5 < x < –1.1 –0.3 < x < 0.1
Answers
Given:
The values in the table represent the graph of a continuous function.
To find:
The interval that must contain an x-intercept.
Solution:
From the given table it is clear that, initially y-values are negative but after negative values we get y=0.44 at x=-1.9.
This signs of y-value are different, it means the graph of continuous function must contain an x-intercept in the interval -2.3 < x < -1.9.
Therefore, the correct option is B.
Answer:
Its , -2.3 < x < -1.9
Step-by-step explanation:
Edge 2020
In the year 2000, the population of Mexico was about 100 million, and it was growing by 1.53% per year. At this growth rate, the function f(x) = 100(1.0153)x gives the population, in millions, x years after 2000. Using this model, in what year would the population reach 106 million? Round your answer to the nearest year.
Answers
Answer:
2004
Step-by-step explanation:

select all the sets of the value that could be the side length of Triangle z.sides are 7,4,10
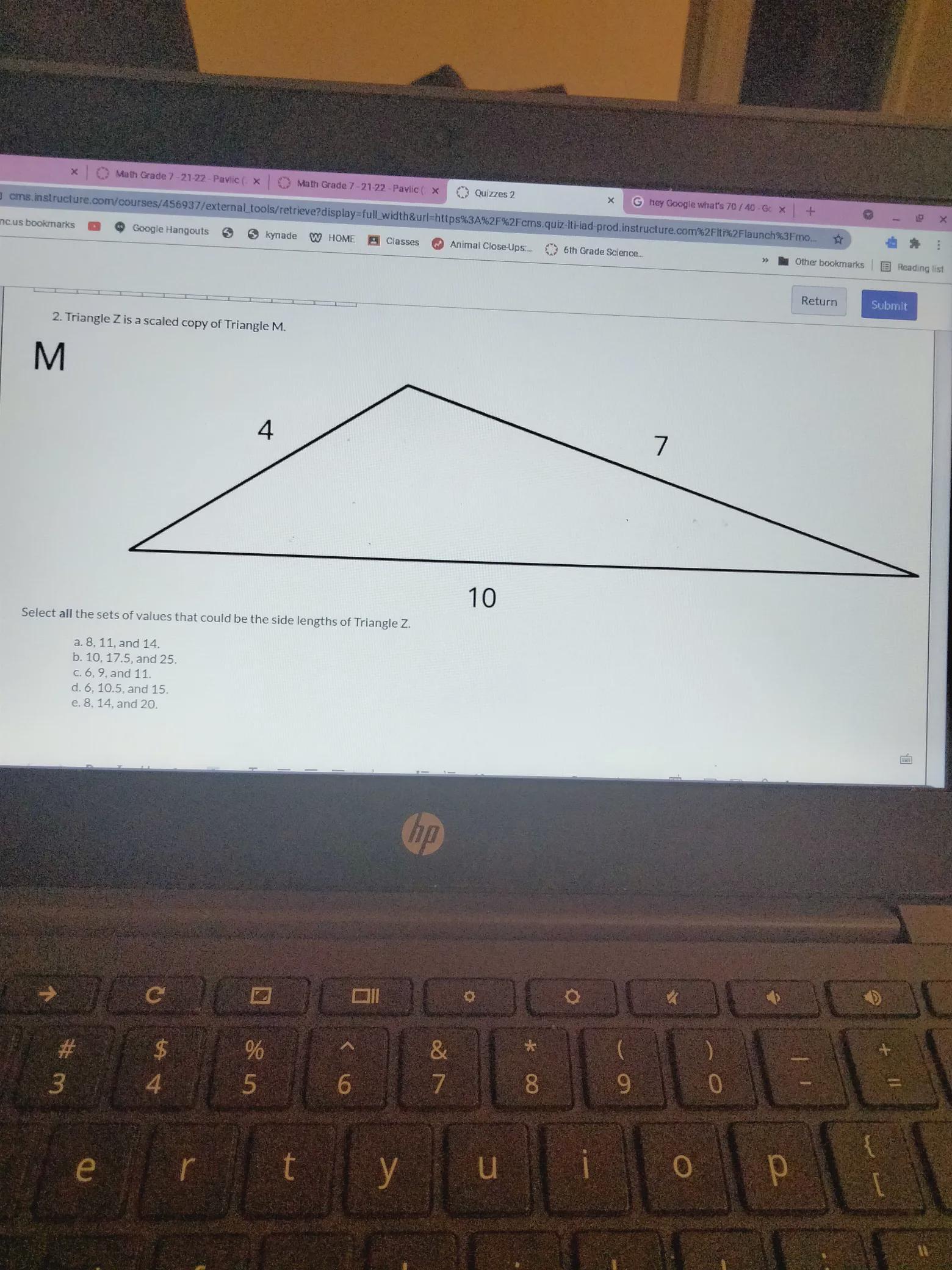
Answers
We will determine if the sets are proportional, if they are, then those will be the sets of lengths that would belong to triangle z, that is:
a.
\(\frac{4}{8}=\frac{7}{11}=\frac{14}{10}\Rightarrow\frac{1}{2}\ne\frac{7}{11}\ne\frac{7}{5}\)So, set a is not one.
b.
\(\frac{4}{10}=\frac{7}{17.5}=\frac{10}{25}\Rightarrow\frac{2}{5}=\frac{2}{5}=\frac{2}{5}\)So, set b could be a set of lengths that belong to triangle z.
c.
\(\frac{4}{6}=\frac{7}{9}=\frac{10}{11}\Rightarrow\frac{2}{3}\ne\frac{7}{9}\ne\frac{10}{11}\)So, set c is not one.
d.
\(\frac{4}{6}=\frac{7}{10.5}=\frac{10}{15}\Rightarrow\frac{2}{3}=\frac{2}{3}=\frac{2}{3}\)So, set d could be a set of lengths that belong to triangle z.
e.
\(\frac{4}{8}=\frac{7}{14}=\frac{10}{20}\Rightarrow\frac{1}{2}=\frac{1}{2}=\frac{1}{2}\)So, set e could be a set of lengths that beling to triangle z.
So, the options that could be candidate are: b, d & e.
In 2016, 595,700 Americans died of (all forms of) cancer.
Assuming a population of 321 million, what was the mortality
rate in units of deaths per 100,000 people?
Answers
The mortality rate will be 180 per 100000 people.
How to calculate the value?From the information, 595,700 Americans died of (all forms of) cancer and there is a population of 321 million.
Therefore the mortality rate will be:
= 595700 / 321 million
= 0.0018
Therefore the mortality rate will be 180 per 100000 people.
Learn more about mortality on:
brainly.com/question/26105007
#SPJ1
Explain how to translate the phrase into an algebraic expression. The difference between four times a number and 10
Answers
Translating the phrase into an algebraic expression for the difference between four times a number and 10 is 4x - 10.
What is an expression?An expression simply refers to the mathematical statements which have at least two terms which are related by an operator and contain either numbers, variables, or both. Addition, subtraction, multiplication, and division are all possible mathematical operations.
Let the number be given as x.
Therefore, 4 times will number will be 4x.
Then, difference between four times a number and 10 will be:
= 4x - 10
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
we laid out strands of lights to decorate the school each strand was 12 feet long how many strands did we need if we needed at least 70 feet of lights
Answers
70/12=5.83
Because you can’t have .8 of a strand, you would need to round up to the next whole number (6)
Reduce this fraction: 5/25x
Answers
Answer:
1/5x
Step-by-step explanation:
1/5x
Tim likes to play video games. If he cancomplete a level in of an hour, howmany levels can he complete in 4hours?
Answers
Given:
Number of levels he can complete in 1 hour = 1 level
To find the number of levels he can complete in 4 hours, we have:
4 * 1 = 4
Hove
Find the average rate of change indicated below.
y = 4x+1
[-1, 1)
A.15
B.3.75
C.1.875
D.7.5
Answers
The average rate of change of the function over the interval is 4
Finding the average rate of changeFrom the question, we have the following parameters that can be used in our computation:
y = 4x + 1
The interval is given as
[-1, 1)
The function is a linear function
This means that it has a constant average rate of change
From y = 4x + 1, we have
Rate = 4
Hence, the rate is 4
Read more about average rate of change at
https://brainly.com/question/17131025
#SPJ1
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
Answers
Answer:
53\(x_{123}\) == 134 cf
Step-by-step explanation:
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
The height of the building is approximately 78.63 meters.
The following is a step-by-step explanation of how to solve the problem. We'll need to use some trigonometric concepts and formulas to find the solution.
Draw a diagram of the situation described in the problem to get a better understanding of the problem. The diagram would have a right-angled triangle with angle of elevation of 66° at the bottom left vertex and another angle of elevation of 53° at the bottom right vertex. The object on top of the building is at the vertex of the triangle. Point M and I on the diagram are points on the horizontal line of sight and on the ground respectively. We can label the diagram with the following values:Angle of elevation from point A = 66°Angle of elevation from point P = 53° Length of line segment AM = h Length of line segment MP = x Length of line segment IP = y Length of line segment MT = 50m. We'll use these values to calculate the length of h, which is the height of the building.Use the tangent ratio to find x:tan 66° = h / x => x = h / tan 66°. Use the tangent ratio to find y:tan 53° = h / y => y = h / tan 53°.We know that x + y = 50, so substituting the expressions for x and y from step 3 gives:h / tan 66° + h / tan 53° = 50h = 50 tan 66° tan 53° / (tan 53° + tan 66°) ≈ 78.63 m.Therefore, the height of the building is approximately 78.63 meters.
For more such questions on height, click on:
https://brainly.com/question/28122539
#SPJ8
area of a floor 19m by 12 m is
Answers
Answer:228m
Step-by-step explanation: 19m x 12m = 228m
Answer: 228m
Step-by-step explanation: Just multiply 19m by 12m. That's how you find area.
What is the difference?
X+5
X+1
x+ 2 x²+2x
O
O
O
O
x²+4x-1
x(x+2)
x²+4x+1
x(x+2)
4
-1(x²+x-2)
x²+6x+1
X(X+2)

Answers
Answer:
its the third one
Step-by-step explanation:
Marcus wants to buy a car for $8,000. He currently has saved $3,450. His job allows him to save $225a week (w). What equation represents his savings (S) to buy a car?
Answers
Answer:
Im guessing your asking how many weeks he needs to work, he needs to work 20.2 weeks to get enough for the car. You can easily make a equation with this answer comment on this if you want me to make the equation for you
Step-by-step explanation:
what is the answer plz tell me and not just say something random

Answers
Answer:1/3+3/5 actually is 14/15 and 11/12-5/6 is 1/12
Step-by-step explanation:
In 1995 the size of a typical personal
computer processor was 3.8 cm x 2.9 cm.
In 2009 a smartphone processor can be
as small as 1.1 cm x 0.8 cm. How much
larger is the 1995 processor than one
found in today's phones?
Answers
The 1995 processor when compared to the processor in today's phones is 12 .5 times larger .
How to find the difference ?To find how much larger the 1995 processor is , you first need to find the area of the processors.
Area of 1995 processor:
= 3. 8 x 2 . 9
= 11. 02 cm ²
Area of 2005 processor :
= 1. 1 x 0. 8
= 0. 88 cm ²
In comparison to the 2009 processor, the 1995 processor is :
= 11. 02 / 0.88
= 12 .5 times larger
Find out more on processors at https://brainly.com/question/614196
#SPJ1
Match each step with the correct ordered description for how to construct a copy of an angle. (There are 10 steps)

Answers
A ray from the vertex of the angle through the point where the two arcs intersect. This ray is a copy of the original angle.
The steps for constructing a copy of an angle:
Step 1: Draw the angle.
Step 2: Place the center of the protractor on the vertex of the angle.
Step 3: Line up the baseline of the protractor with one of the angle's rays.
Step 4: Read the degree measure where the other ray crosses the protractor.
Step 5: Draw a ray from the vertex of the angle to the right.
Step 6: Use a ruler to mark the same distance on the ray that was just drawn.
Step 7: Draw a ray from the vertex through the point just marked on the ray.
This is the copy of the angle's second ray.
Step 8: Use a compass to draw an arc centered at the vertex of the original angle that passes through one of the angle's rays.
Step 9: Without adjusting the compass, draw another arc that intersects the previous arc at a point.
Step 10: Draw a ray from the vertex through the point where the two arcs intersect.
This is the copy of the original angle.
Using a compass, draw an arc centered on the vertex of the original angle passing through one of the angle rays. Place the tip of the
compass on the vertex of the original angle and draw an arc that intersects one of the angle rays.
Draws another arc that intersects the previous arc at a point without adjusting the compass.
Draw a second arc that intersects the first arc at another point, keeping the compass latitude.
Using a ruler or ruler, draw a ray from the vertex of the angle through the point where the two arcs intersect. This ray is a copy of the original angle.
For more related questions on original angle.:
https://brainly.com/question/27243531
#SPJ8
What is the base area of Box 3? x2 + x
edge
Answers
The expression of base area of box will be 4x + x²
The area of a a rectangle occupies is the space it takes up inside the limitations of its four sides. The dimensions of a rectangle determine its area. Basically, the area formula is the product of the rectangle's length and width.
Given,
Length = 4+x
width = x
height = x²+1
We have to find the expression of base area of box
Given the length, width, and height
The formula for area of rectangle is as follow:
Area of rectangle = length x width
Area of rectangle = (4+x) x (x)
Area of rectangle = 4x + x²
Hence the expression of base area of box will be 4x + x²
Learn more about area of rectangle here:
https://brainly.com/question/13048427
#SPJ10
7+5x>-13..............
Answers
ANSWER
\(x>-4\)EXPLANATION
We want to solve for x in the inequality:
\(7+5x>-13\)First, subtract 7 from both sides of the equation:
\(\begin{gathered} 7+5x-7>-13-7 \\ 5x>-20 \end{gathered}\)Divide both sides by 5:
\(\begin{gathered} \frac{5x}{5}>-\frac{20}{5} \\ x>-4 \end{gathered}\)That is the answer.
When Ibuprofen is given for fever to
children 6 months of age up to 2 years, the
usual dose is 5 milligrams (mg) per kilogram
(kg) of body weight when the fever is under
102.5 degrees Fahrenheit. How much
medicine would be usual dose for a 18
month old weighing 21 pounds?
milligrams
Round your answer to the nearest milligram.
Answers
Answer: The usual dose for an 18-month-old weighing 21 pounds is 48 mg of ibuprofen.
Step-by-step explanation: To find the usual dose of ibuprofen for a child, we need to follow these steps:
Convert the child’s weight from pounds to kilograms. One pound is equal to 0.4536 kilograms, so we multiply 21 by 0.4536 to get 9.5256 kilograms.Multiply the child’s weight in kilograms by the dose per kilogram. The dose per kilogram is 5 mg when the fever is under 102.5 degrees Fahrenheit, so we multiply 9.5256 by 5 to get 47.628 mg.Round the result to the nearest milligram. To round a number to the nearest milligram, we look at the digit after the decimal point. If it is 5 or more, we add one to the digit before the decimal point and drop the rest. If it is less than 5, we keep the digit before the decimal point and drop the rest. In this case, the digit after the decimal point is 6, which is more than 5, so we add one to the digit before the decimal point and drop the rest. The result is 48 mg.Therefore, the usual dose for an 18-month-old weighing 21 pounds is 48 mg of ibuprofen. Hope this helps, and have a great day! =)
1. A. What is the formula for the Pythagorean Theorem? (1 point)
B. Find the missing leg of the triangle using the Pythagorean Theorem. Remember that drawings may not be to scale (Round to the nearest tenth).
Show your work. (4 points)
20 ft
18 ft
x

Answers
Answer:
side 1^2 + side 2 ^2 = hypotenuse ^ 2
18^2 + 20^2 = hypotenuse^2
324 + 400 = 724
hypotenuse^2 = 724
hypotenuse = 26.9072480941474
hypotenuse = 26.9
Step-by-step explanation: