Show that for the array \( A=\{10,9,8,7,6,5,4,3\} \), QUICKSORT runs in \( \Theta\left(\mathrm{n}^{2}\right) \) time.
Answers
The QUICKSORT algorithm runs in Θ(n²) time for the given array A = {10, 9, 8, 7, 6, 5, 4, 3}, as demonstrated by the worst-case upper bound of O(n²) and the lower bound of Ω(n²) based on the properties of comparison-based sorting algorithms.
To show that the QUICKSORT algorithm runs in Θ(n²) time for the given array A = {10, 9, 8, 7, 6, 5, 4, 3}, we need to demonstrate both the upper bound (O(n²)) and the lower bound (Ω(n²)).
1. Upper Bound (O(n²)):
In the worst-case scenario, QUICKSORT can exhibit quadratic time complexity. For the given array A, if we choose the pivot element poorly, such as always selecting the first or last element as the pivot, the partitioning step will result in highly imbalanced partitions.
In this case, each partition will contain one element less than the previous partition, resulting in n - 1 comparisons for each partition. Since there are n partitions, the total number of comparisons will be (n - 1) + (n - 2) + ... + 1 = (n² - n) / 2, which is in O(n²).
2. Lower Bound (Ω(n²)):
To show the lower bound, we need to demonstrate that any comparison-based sorting algorithm, including QUICKSORT, requires at least Ω(n²) time to sort the given array A. We can do this by using a decision tree model. For n elements, there are n! possible permutations. Since a comparison-based sorting algorithm needs to distinguish between all these permutations, the height of the decision tree must be at least log₂(n!).
Using Stirling's approximation, log₂(n!) can be lower bounded by Ω(n log n). Since log n ≤ n for all positive n, we have log₂(n!) = Ω(n log n), which implies that the height of the decision tree is Ω(n log n). Since each comparison is represented by a path from the root to a leaf in the decision tree, the number of comparisons needed is at least Ω(n log n). Thus, the time complexity of any comparison-based sorting algorithm, including QUICKSORT, is Ω(n²).
By combining the upper and lower bounds, we can conclude that QUICKSORT runs in Θ(n²) time for the given array A.
To know more about QUICKSORT algorithm, refer to the link below:
https://brainly.com/question/13257594#
#SPJ11
Complete Question:

Related Questions
A bakery offers a sale price of 2.55 for 4 muffins.what is the price per dozen?
I hope someone answers fast
And explain what you did
Answers
Answer: $7.65 for a dozen/12
Step-by-step explanation: 2.55 x 3
Situation: A DJ will play music. The DJ charges $20 per hour plus a $50 appearance fee. Represent the relationship
between the number of hours the DJ works and the total cost of hiring the DJ.
Table:
Graph:
Process
T
Draw or add in les
Algebraic rule:
Answers
Does the following linear programming problem exhibit infeasibility, unboundedness, or alternate optimal solutions? Explain.
Min 1X + 1Y
s.t. 5X + 3Y < 30
3X + 4Y > 36
Y < 7
X , Y > 0
Answers
The given linear programming problem does not exhibit infeasibility, unboundedness or alternate optimal solutions.
Linear programming is an optimization technique to solve optimization problems. Linear programming is the process of optimizing a linear objective function of several variables subject to constraints on the variables. A linear programming model always has an objective function and constraints expressed as linear equations or inequalities.
Linear programming can be solved graphically or by using the simplex algorithm. The given linear programming problem isMin 1X + 1Ys.t. 5X + 3Y < 303X + 4Y > 36Y < 7X , Y > 0There are three constraints in the given linear programming problem, and each of them can be represented by a straight line in a two-dimensional graph. The feasible region is the shaded area where all the constraints are satisfied.
The objective function can be represented by a straight line as well.The feasible region in the given linear programming problem is not empty, which means there is at least one feasible solution. The feasible region is bounded, which means the optimal solution exists.
The objective function has a finite minimum value, which means the optimal solution is unique. Therefore, the given linear programming problem does not exhibit infeasibility, unboundedness or alternate optimal solutions.
See more about linear programming at: https://brainly.com/question/30591970
#SPJ11
y= -x + 1 and y= 2/3x - 4 What is the solution to the system of equations?
Answers
Answer:
x=3 /
steps: (For x)
Turn the equation into --> -x+1 = 2/3x-4
Next is the multiply the equation by 3 to make isolating x easier so it becomes --> -3x+3=2x-12
Now arrange the terms to where variables are on a side and constants are on a side
it should look like --> -3×-2x=-12-3
Now combine like terms --> -5x=-15
finally just divide by -5 on both sides
x=3
For y:
substitute X for either of the equations
y=2/3 x 3-4
y=-2
The solution is (3,-2)
A car rental agency charges a base fee of $50 plus an additional charge of $0.40 for every mile driven. The total charge, c, is given by the equation. c = 50 + 0.40m, where m represents the miles driven. When Mr. Sims rented a car, his total charge was $178.00. How many miles did Mr. Sims drive the car? *
Answers
Answer:
Mr. Sims drove 320 miles.
Step-by-step explanation:
c = 50 + 0.40m
178 = 50 + 0.40m
128 = 0.40m
m = 320
Help me please I don't get it, it doesn't explain how to do it

Answers
The area of the shaded region is 15 \(yd^2\).
What is area of the shape?The region that an object's shape defines as its area. The area of a figure or any other two-dimensional geometric shape in a plane is how much space it occupies.
Here in the given diagram contains right triangle and rectangle.
We need to find both triangle and rectangle area in order to find area of shaded region.
Now Base= 3+4 = 7 yd , Height h =6 yd. Then,
Area of triangle A = \(\frac{1}{2}bh\) square unit
=> A = \(\frac{1}{2}\times7\times6\)
=> A = \(7\times3 = 21 yd^2\)
Now breadth b = 3 yd , Width w=2 yd, Then
Area of rectangle = bw square unit.
=> A = 3×2 = 6 \(yd^2\)
Now area of the shaded region = Area of triangle - Area of rectangle
=> Area of shaded region = 21-6 = 15 \(yd^2\).
Hence the area of the shaded region is 15 \(yd^2\).
To learn more about area refer the below link
https://brainly.com/question/20110859
#SPJ1
What’s the mean,median,mode, and range of 5,28,16,32,5,16,48,29,5,35
Answers
Answer:
Step-by-step explanation:
5, 5, 5, 16, 16, 28, 29, 32, 35, 48
Mode: 5, 16
Median: 44/2 = 22
range: 48 - 5 = 43
mean: (5 + 5 + 5 + 16 + 16 + 28 + 29 +32 + 35 + 48)/10 = 219/10 = 21.9
In the polynomial shown in the graph below, are there any places that could be described as either a local minimum or local maximum? Neither? Both?
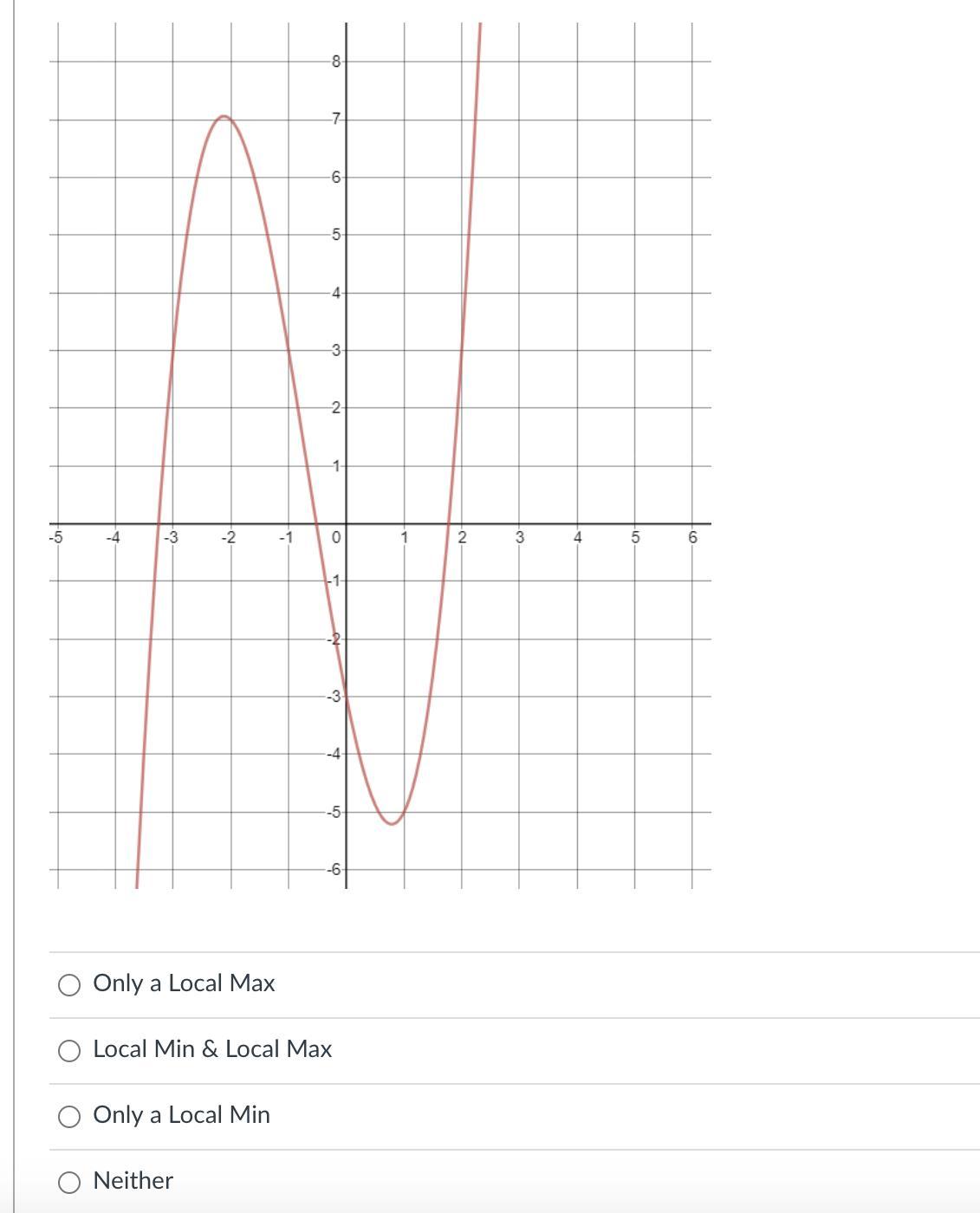
Answers
Answer:
Local Min and Local Max
Step-by-step explanation:
Since our end behavior of our graph is goes on to infinity and negative infinity, we know that we will not have an absolute min or max. However, we will have relative/local min and max.
The local min and max are mins and maxes relative to the surrounding points. We see that our local min would happen around x ≈ 0.75 and our local max will happen at x ≈ -1.9.
If a radioactive substance is quickly decaying at a rate of 13% per hour approximately how much of a 200 pound sample remains after one day? *
A. 7.1
B. 2.3
C. 25.6
D. 15.6
Answers
Answer: 7.1
Step-by-step explanation:
Exponential functions: y=ab^x
A = starting value
R= rate ex: 3% = .03
B= 1 + r
Then write your exponential function
Helmets and lunches: The scatterplot shows the relationship between socioeconomic status measured as the percentage of children in neighborhood receiving reduced-fee lunches at school (lunch) and the percentage of bike riders in the neighborhood wearing helmets (helmet). The average percentage of children receiving reduced-fee lunches is 30.8% with standard deviation of 26.7% and the average percentage of bike riders wearing helmets is 38.8% with standard deviation of 16.9%. (a) If the R? for the least-squares regression line for these data is 72%, what is the correlation 60% between lunch and helmet? 1 (b) Calculate the slope and intercept for the least-squares regression line for these data. 40% (c) Interpret the intercept of the least-squares regression line in the context of the application_ 6 (d) Interpret the slope of the least-squares regression 3 20% line in the context of the application: (e) What would the value of the residual be for 2 neighborhood where 40% of the children receive 0% reduced-fee lunches and 40% of the bike riders 0% 20% 40% 60% 80% wear helmets? Interpret the meaning of this Rate of Receiving a Reduced-Fee Lunch residual in the context of the application
Answers
The answers are:
a. The correlation between lunch and helmet is 84.8%.
b. The slope is 0.538 and the intercept is 22.1.
c. It means that even if no children receive reduced-fee lunches, there would still be a baseline percentage of 22.1% of bike riders wearing helmets.
d. It means that for every 1% increase in the percentage of children receiving reduced-fee lunches, there is an expected increase of 0.538% in the percentage of bike riders wearing helmets.
e. The residual is 40 - 41.9 = -1.9%. In this context, the negative residual suggests that the actual percentage of bike riders wearing helmets is slightly lower than the predicted value, given the percentage of children receiving reduced-fee lunches.
(a) The correlation coefficient (r) between lunch and helmet can be calculated using the formula: r = (R^2)^(1/2). Given that R^2 is 72%, we can find r = sqrt(0.72) = 0.848.
(b) The slope (b) and intercept (a) for the least-squares regression line can be calculated using the formulas: b = r * (SDy / SDx) and a = mean_y - b * mean_x. With SDy = 16.9%, SDx = 26.7%, mean_y = 38.8%, and mean_x = 30.8%, we can find b = 0.848 * (16.9 / 26.7) = 0.538 and a = 38.8 - 0.538 * 30.8 = 22.1.
(c) The intercept (a) represents the predicted percentage of bike riders wearing helmets when the percentage of children receiving reduced-fee lunches is 0.
(d) The slope (b) represents the change in the percentage of bike riders wearing helmets for each 1% increase in the percentage of children receiving reduced-fee lunches.
(e) To calculate the residual for a neighborhood where 40% of children receive 0% reduced-fee lunches and 40% of bike riders wear helmets, we can use the formula: residual = observed_y - predicted_y. Given that observed_y is 40% and predicted_y can be calculated as a + b * x, where x is 40%, we have predicted_y = 22.1 + 0.538 * 40 = 41.9%.
Learn more about correlation from the given link:
https://brainly.com/question/30116167
#SPJ11
Find the radius of convergence R of the series.
[infinity] n
bn (x − a)n, b > 0
n = 1
R =
Find the interval of convergence of the series. (Enter your answer using interval notation.)
Answers
The interval of convergence is from (a - b) to (a + b), where b is a positive number.
1. The radius of convergence R is given by the formula R = 1/|b|.
2. The interval of convergence is given by the formula (a - b, a + b).
The radius of convergence R of a series is a measure of how quickly the series converges. It is calculated by taking the inverse of the coefficient of the term with the highest power of the variable in the series. In this case, the coefficient of the highest power of the variable is b, so the radius of convergence is 1/|b|.
The interval of convergence is the region in which the series converges. It is determined by the coefficient of the term with the highest power of the variable in the series. In this case, the coefficient of the highest power of the variable is b, so the interval of convergence is (a - b, a + b). This means that the series converges for values of x in the range from (a - b) to (a + b).
Learn more about interval here
https://brainly.com/question/24131141
#SPJ4
a mean of 32 kilograms and a standard deviation of 0.89 kilograms. Complete parts a through d below. a. What is the probability that a filled bag will weigh less than 31.7 kilograms? The probability is (Round to four decimal places as needed.)
Answers
The probability that a filled bag will weigh less than 31.7 kilograms is 0.3674 (approx) when rounded to four decimal places.
Given that mean of filled bag is 32 kg and the standard deviation is 0.89 kg.
To find the probability that a filled bag will weigh less than 31.7 kg, we need to standardize the variable and find the area under the standard normal curve.The standard normal distribution has mean 0 and standard deviation 1.
Let X be the weight of the filled bag.Then,
Z = (X - μ) / σ
= (31.7 - 32) / 0.89
= -0.337079
Possible ways of rounding depends on the instructions provided to the students. Here, rounding to 4 decimal places is necessary because it has been explicitly mentioned in the question.
Now, we need to find the probability that a filled bag will weigh less than 31.7 kilograms, which is same as finding the probability that Z is less than -0.337079 from the standard normal distribution table using the standard normal distribution.p(Z < -0.337079) = 0.3674 (approx)
Therefore, the probability that a filled bag will weigh less than 31.7 kilograms is 0.3674 (approx) when rounded to four decimal places.Note: The question is asking to round the answer to four decimal places, which makes it important to give the answer as 0.3674 (approx).
Learn more about the probability from the given link-
https://brainly.com/question/30390037
#SPJ11
ab is parallel to cd what is the value of x?

Answers
Answer:
D
Step-by-step explanation:
the angle vertically opposite 30° is also 30° since vertically opposite angles are congruent.
then this angle and x are same- side interior angles and sum to 180°, that is
x + 30° = 180° ( subtract 30° from both sides )
x = 150°
What is the correct numerical expression for "9 times 4 added to the difference of 3 and 2?"
O9x4+ (3-2)
09x(4+3)-2
09+(4x3)+2
09-2x4+3
Answers
The correct numerical expression for "9 times 4 added to the difference of 3 and 2" is:
\(9 x 4 + (3 - 2)\)
What is expression?In mathematics, an expression is a combination of numbers, variables, operators, and/or functions that can be evaluated to produce a value. Expressions can be simple or complex, and can involve arithmetic operations (such as addition, subtraction, multiplication, and division), as well as more advanced mathematical concepts such as exponents, logarithms, and trigonometric functions.
Expressions are often used in mathematical equations and formulas, and can be used to represent real-world situations and problems. For example, the expression "2x + 3y" might be used to represent the cost of buying two items that cost x dollars each and three items that cost y dollars each.
It's important to distinguish expressions from equations, which are statements that assert that two expressions are equal to each other. An equation involves an expression on each side of the equal sign, whereas an expression does not contain an equal sign.
The correct numerical expression for "9 times 4 added to the difference of 3 and 2" is:
\(9 x 4 + (3 - 2)\)
First, we evaluate the difference between 3 and 2, which is 1. Then we multiply 9 and 4, which is 36. Finally, we add 36 and 1 to get the answer:
\(36 + 1 = 37\)
To learn more about mathematical expressions from the given link
brainly.com/question/30091997
Simplify the expression (2x-9)(x+6)
Answers
Answer:
2x²+3x-54
Step-by-step explanation:
(2x-9)(x+6)
=x(2x-9)+6(2x-9)
=2x²-9x+12x-54
=2x²+3x-54
G2.
A water tank contains 55 gallons of water when
Bryan starts to fill it, Water flows into the tank at a
rate of 8 gallons per minute. Write the equation to
represent this situation.
Answers
Answer: 55+8= x 1 minute
Step-by-step explanation:
Answer:
55gallons divided by 8 gallons
Step-by-step explanation: First you have to figure out what you are working to get the answer out of which is 55 gallons of water then you see how much you are taking into to see how many 8's can go into 55 then you get you answer so the equation should look like this 55/8
Solve for m angleUVW if m angle UVX = 40° and m angle XVW = 68°

Answers
Answer:
The measure of the obtuse angle marked UVW is 108
Step-by-step explanation:
Here, we want to get the measure of the angle marked UVW
To get this, we refer to the given diagram
From the diagram;
UVW = UVX + XVW
UVW = 68 + 40
UVW = 108 degrees
A sample survey interviews SRSs of 500 female college students and 550 male college students. Each student is asked whether he or she worked for pay last summer. In all, 410 of the women and 484 of the men say "yes".Take Pm and Pf to be the proportions of all college males and females who worked last summer. We conjectured before seeing the data that men are more likely to work. The hypotheses to be test are:a. H₀: Pm - Pf = 0 vs. Hₐ: Pm - Pf ≠ 0b. H₀: Pm - Pf = 0 vs. Hₐ: Pm - Pf > 0c. H₀: Pm - Pf = 0 vs. Hₐ: Pm - Pf < 0d. H₀: Pm - Pf > 0 vs. Hₐ: Pm - Pf = 0e. H₀: Pm - Pf ≠ 0 vs. Hₐ: Pm - Pf = 0
Answers
The correct hypotheses to be tested based on the given information are H₀: Pm - Pf = 0 vs. Hₐ: Pm - Pf < 0 (option c).
These hypotheses reflect the conjecture that men are more likely to work than women. In hypothesis testing, the null hypothesis (H₀) typically represents the assumption of no difference or no effect, while the alternative hypothesis (Hₐ) represents the claim or hypothesis we want to support.
In this case, the null hypothesis states that there is no difference between the proportions of male and female college students who worked last summer (Pm - Pf = 0). The alternative hypothesis states that the proportion of male college students who worked last summer is greater than the proportion of female college students who worked (Pm - Pf < 0).
By testing these hypotheses using appropriate statistical methods, we can determine if the observed data supports the claim that men are more likely to work than women or if there is no significant difference between the two proportions. The correct option is c.
To know more about hypotheses:
https://brainly.com/question/32562440
#SPJ4
The sine and cosine of an acute angle are equal. What is the value of angle?
1)30°
2)45°
3)60°
4)Sine and Cosine will never be equal.
Answers
The sine and the cosine of the acute angle are the same for θ = π / 4. (Correct choice: 2)
To what angles both the sine and the cosine have the same value?
Acute angles are angles whose measures are greater than 0° and less than 90°. According to the statement, we must find at least a value such that sin θ = cos θ:
sin θ = cos θ Given
sin θ / cos θ = 1 Compatibility with multiplication / Existence of multiplicative inverse / Modulative property
tan θ = 1 Definition of tangent
θ = π / 4 Inverse trigonometric function / Result
In a nutshell, the sine and the cosine of the acute angle are the same for θ = π / 4. (Correct choice: 2)
To learn more on trigonometric functions: https://brainly.com/question/14746686
#SPJ1
The mean of the data is 18.25. find the variance. find the standard deviation.
Answers
The standard deviation is the square root of the variance and is used to measure how spread out the data is. To calculate the standard deviation, take the square root of the variance.
What is variance?Variance is the measure of how far a set of numbers are spread out from their average value. It is a measure of how much variation or dispersion exists from the average. Variance is represented as the square of the standard deviation, which is a measure of the spread of numbers in a set.
The mean of the data is 18.25. The variance is a measure of the spread of the data away from the mean, and is calculated by taking the average of the squared differences from the mean. To calculate the variance, subtract the mean from each data point, square this result and add up the values. Then divide this sum by the number of data points minus one.
For example, if the data set contains the values 10, 15, 20, 25 and 30 then the mean is 18.25. Subtracting the mean from each data point gives -8.25, -3.25, 1.75, 6.75, 11.75. Squaring each of the differences gives 68.0625, 10.5625, 3.0625, 45.5625, 137.0625. Adding these results together gives 264.3125. Dividing this by 4 (the number of data points minus one) gives 66.075. Taking the square root of this gives 8.1 as the standard deviation.
For more questions related to standard deviation
https://brainly.com/question/24298037
#SPJ1
The variance of the given data is calculated to be 118.63 and the standard deviation is 10.89.
What does variance mean?The variance of the data is a measure of how far the data points are spread out from the mean. It is calculated by taking the differences between each data point and the mean, squaring the differences, and then taking the average of those squared differences.
For our data, the mean is 18.25. To find the variance, we can subtract 18.25 from each of the data points and square the differences. Then we can add up all of the squared differences and divide by the number of data points.
Variance = (2 - 18.25)² + (3 - 18.25)² + (4 - 18.25)² + (18 - 18.25)² + (20 - 18.25)² + (25 - 18.25)²
= (15.752 + 14.752 + 13.752 + 0.752 + 1.752 + 6.752) ÷ 6
= (255.2 + 217.2 + 190.2 + 0.6 + 3.0 + 45.8) ÷ 6
= 711.8 ÷ 6
Variance = 118.63
To find the standard deviation, we take the square root of the variance.
Standard deviation = √118.63
Standard deviation = 10.89
For more questions related to standard deviation
https://brainly.com/question/24298037
#SPJ1
Question:
The mean of the data is 18.25. Find the variance. Find the standard deviation.
Data: 2, 3, 4, 18, 20, 25
Find an equation of the circle that has center (-4,3) and passes through (6,-4).
Answers
Answer:
\((x+4)^2+(y-3)^2=149\)
Step-by-step explanation:
The equation of a circle is \((x-h)^2+(y-k)^2=r^2\) where \((h,k)\) is the center of the circle and \(r\) is the radius of the circle.
Given that \((h,k)\rightarrow(-4,3)\) and it passes \((6,-4)\), their distance between each other must the radius of the circle, so we can use the distance formula to find the radius:
\(d=\sqrt{(y_2-y_1)^2+(x_2-x_1)^2}\\\\d=\sqrt{(-4-3)^2+(6-(-4))^2}\\\\d=\sqrt{(-7)^2+10^2}\\\\d=\sqrt{49+100}\\\\d=\sqrt{149}\)
Therefore, if the length of the radius is \(r=\sqrt{149}\) units, then \(r^2=149\), making the final equation of the circle \((x+4)^2+(y-3)^2=149\)

Help ASAP it’s either
68degrees
110 degrees
136 degrees
or 112 degrees

Answers
Answer:112
Step-by-step explanation: Line SW is 180 degrees since it is a straight line. Subtract angle TBU 18 and angle UBW 50 from line SW 180 to get angle SBU which is 112.
*PLEASE ANSWERRR!!! NEED HELP ASAP*

Answers
Answer:
The Mean is increased by 2.
Step-by-step explanation:
Mark brainliest please good luck with that test ;)
A researcher wants to estimate the average amount of calories in a large French Fries order in McDonalds. He wants a 95 % level of confidence with a margin of error of 10 calories. How many orders he needs to sample
Answers
The researcher would need to sample at least 193 large French Fries orders to estimate the average amount of calories with a 95% level of confidence and a margin of error of 10 calories.
To determine the sample size required to estimate the average amount of calories in a large French Fries order in McDonald's, we can use the following formula:
n = (Z^2 * σ^2) / E^2
where:
n = sample size
Z = the z-score associated with the desired confidence level (for a 95% confidence level, Z = 1.96)
σ = the population standard deviation (if unknown, a conservative estimate can be used)
E = the desired margin of error
Since we don't know the population standard deviation, let's assume a conservative estimate of 50 calories based on similar studies. Thus, the formula becomes:
n = (1.96^2 * 50^2) / 10^2 = 192.08
Rounding up to the nearest whole number, the researcher would need to sample at least 193 large French Fries orders to estimate the average amount of calories with a 95% level of confidence and a margin of error of 10 calories.
Learn more about average amount here:
https://brainly.com/question/18366065
#SPJ11
A civil engineering company is hired to design a new drainage system for your town. To construct one of the storm drains, a sheet of metal that is 15.25 feet wide is folded on both sides. 1. Describe the drain that has the maximum cross-sectional area. Include at least two different representations in your reasoning. description. Show all work and explain your
Answers
The 15,25 feet width of the sheet metal gives a drain that has a maximum cross-sectional area of approximately, 29.07 square feet. The width of the drain that has the maximum cross sectional area is 7.625 feet, and the depth of the drain is 3.8125 feet.
What is the dimensions of a rectangular open drain?The dimensions of an open drain include the width and the depth of the drain.
The width of the sheet metal = 15.25 feet
Let x represent the depth of the drain. The width, w, of the drain is found from x as follows; w = 15.25 - 2·x
Area of a rectangle = Width × Height (or depth)
The area of the rectangular drain is therefore; A = w × x
Which gives; A = x × (15.25 - 2·x) = 15.25·x - 2·x²
Given that the coefficient of x² is negative, the maximum volume is given by the point at which the rate of change of the the area is zero as follows;
\(At \ the \ maximum \ volume, \ \dfrac{dA}{dx} = 0 = \dfrac{d}{dx} \left(15.25\cdot x - 2\cdot x^2\right) = 15.25 - 4\cdot x\)
At the point where the volume is maximum, we have;
\(x = \dfrac{15.25}{4} = 3.8125\)
The depth of the drainage that gives the maximum volume is x = 3.8125 feet
w = 15.25 - 2·x
Therefore;
w = 15.25 - 2×3.8125 = 7.625
The width of the drainage is, w = 7.625 feet
\(A_{max}\) = 15.25×3.8125 - 2×3.8125² ≈ 29.07
The area of the drain that gives the maximum area is, \(A_{max}\) = 29.07 ft²
The description of the drain that has the maximum cross sectional area are as follows;
Width; 7.625 feet
Depth; 3.8125 feet
Area; Approximately 29.07 ft.²
Learn more about the maximum value of a function here:
https://brainly.com/question/5722003
#SPJ1

What does multiplicity mean in math?
Answers
The phrase "number of values for which a certain condition holds" is referred to as multiplicity. The phrase, for instance, can be used to describe the magnitude of the totient valence function or the frequency with which a given polynomial equation has a root at a specific location.
Let z_0 be a root of a function f, and let n be the least positive integer n such that f^((n))(z_0)!=0. Then the power series of f about z_0 begins with the nth term,
f(z)=sum_(j=n)^infty1/(j!)(partial^jf)/(partialz^j)|_(z=z_0)(z-z_0)^j,
and f is said to have a root of multiplicity (or "order") n. If n=1, the root is called a simple root '
The multiplicity of a member of a multiset in mathematics is the number of times the member appears in the multiset. The multiplicity of a root, for instance, is how many times a given polynomial has a root at a particular point.
It's crucial to understand the concept of multiplicity in order to correctly count without mentioning exceptions (for example, double roots counted twice). Thus, "counted with multiplicity" is used.
This can be highlighted by counting the number of different elements, as in "the number of separate roots," if multiplicity is disregarded. However, multiplicity is always taken into account when a set (as opposed to a multiset) is established, therefore the word "different" is not necessary.
Hence ,Multiplicity means the quality or state of being multiple or various. and
the number of components in a system (such as a multiplet or a group of energy levels)
Tp know more about Mutiplicity visit : brainly.com/question/5992872
#SPJ4
Let z_0 be a root of a function f, and let n be the least positive integer n such that f^((n))(z_0)!=0. Then the power series of f about z_0 begins with the nth term,
f(z)=sum_(j=n)^infty1/(j!)(partial^jf)/(partialz^j)|_(z=z_0)(z-z_0)^j,
and f is said to have a root of multiplicity (or "order") n. If n=1, the root is called a simple root '
The multiplicity of a member of a multiset in mathematics is the number of times the member appears in the multiset. The multiplicity of a root, for instance, is how many times a given polynomial has a root at a particular point.
Florian ran 1.2 miles and walked 4.8 laps around the path at the park for a total distance of 3.6 miles.
Which shows the correct equation and value of x , the distance of 1 lap around the path at the park?
Answers
The equation and value of x , the distance of 1 lap around the path at the park is 4.8x + 1.2 = 3.6.
What is Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides. LHS = RHS is a common mathematical formula.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given:
Florian ran 1.2 miles and walked 4.8 laps around the path at the park for a total distance of 3.6 miles.
As, we know the number of them (4.8) would be multiplied by the variable (x). We also know that 1.2 is the constant.
So, the equation can be framed as
4.8x + 1.2 = 3.6
4.8x = 2.4
x = 0.5
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ9
The question attached here seems to be incomplete the remaining portion is given below:
3.6 x + 1.2 = 4.8; x = 1 mile
4.8 x + 1.2 = 3.6; x = 1 mile
3.6 x + 1.2 = 4.8; x = 0.5 mile
4.8 x + 1.2 = 3.6; x = 0.5 mile
5 x = negative 58
Triangle Proportionality- Find the missing side (subtract)

Answers
Answer:
10
Step-by-step explanation:
Find a vector equation of the line through (6,4.2) that is perpendicular to the lines r, (t) (8-2t,1+8t,9-5t) and r2(t)--2t,1t9-where t0 corresponds to the first given point.
Answers
A vector equation of the line through (6,4.2) that is perpendicular to the lines r1(t) = (8-2t, 1+8t, 9-5t) and r2(t) = (-2t, 1, 9) is:
r(t) = <6, 4.2, z> + t<2, -5, 0>
where z is a constant that satisfies the equation:
(8-2t - 6)(2) + (1+8t - 4.2)(-5) + (9-5t - z)(0) = 0
To find the equation of the line through the given point (6,4.2) that is perpendicular to the two given lines, we need to find the direction vector of the new line that is perpendicular to both of the given lines. The direction vector is the cross product of the direction vectors of the two given lines.
After finding the direction vector, we can use it to write the vector equation of the line passing through the given point (6,4.2). The constant z is found by substituting the x and y coordinates of the given point into the equation of the line.
The final equation is a vector equation of the desired line.
For more questions like Equation click the link below:
https://brainly.com/question/29657983
#SPJ11
a rectangular room is 3 3 times as long as it is wide, and its perimeter is 56 56 meters. find the dimension of the room.
Answers
Consequently, the room has a 7 meter width. The room's length is
\(= 7 * 3 meters = 21 meters\)
What is rectangle?
A rectangle in Euclidean plane geometry is a quadrilateral with four right angles. You might also describe it as follows: a quadrilateral that is equiangular, which indicates that all of its angles are equal. The parallelogram might also have a straight angle. Squares are rectangles with four equally sized sides. A quadrilateral of the shape of a rectangle has four 90-degree vertices and equal parallel sides. As a result, it is sometimes referred to as an equirectangular rectangle. Because its opposite sides are equal and parallel, a rectangle is also known as a parallelogram.
Given that the length of the rectangular space is three times its breadth
The chamber has a 56-meter perimeter.
Assume that the room's width is x.
As a result, the room is three times as long.
The room's perimeter is now equal to 2(3x + x).
\(Here, 2(3x + x) = 56\\ 2 * 4x = 56\\ 8x = 56\\ x = 7.\)
Consequently, the room has a 7 meter width.
The room's length is
\(= 7 * 3 meters\\= 21 meters\)
To know more about Rectangle visit:
https://brainly.com/question/29123947
#SPJ4