Question 2. Determine the relative maxima and minima of f(x)=2x³-3x². Also describewhere the function is increasing and decreasing:

Answers
The given function is:
\(f(x)=2x^3-3x^2\)It is required to find the relative maxima and minima, and then describe where the function is increasing or decreasing.
Find the derivative of the function:
\(\begin{gathered} f^{\prime}(x)=3(2)x^{3-1}-2(3)x^{2-1} \\ \Rightarrow f^{\prime}(x)=6x^2-6x \end{gathered}\)Substitute f'(x)=0 to find the critical points:
\(\begin{gathered} 6x^2-6x=0 \\ Factor\text{ the expression on the left:} \\ \Rightarrow6x(x-1)=0 \\ \text{ Equate the factors to zero:} \\ \Rightarrow6x=0\text{ or }x-1=0 \\ \Rightarrow x=0\text{ or }x=1 \end{gathered}\)Find the second derivative of the function:
\(\begin{gathered} f^{\prime}(x)=6x^2-6x \\ \text{ Find the derivative of both sides:} \\ \Rightarrow f^{\doubleprime}\left(x\right)=12x-6 \end{gathered}\)Substitute the critical points x=0 and x=1 into the second derivative:
\(\begin{gathered} f^{\doubleprime}\left(0\right)=12(0)-6=-6 \\ f^{\doubleprime}\left(1\right)=12(1)-6=6 \end{gathered}\)Since the second derivative is negative at x=0, it follows from the second derivative test, that the function is maximum at x=0.
Since the second derivative is positive at x=1, it follows from the second derivative test, that the function is minimum at x=1.
Next, calculate the function values at x=0, and x=1:
\(\begin{gathered} f(x)=2x^3-3x^2 \\ \Rightarrow f(0)=2(0)^3-3(0)^2=0 \\ \Rightarrow f(1)=2(1)^3-3(1)^2=2-3=-1 \end{gathered}\)The relative maximum is 0 at x=0.
The relative minimum is -1 at x=-1.
Recall that a function is increasing in the interval where its derivative is positive (greater than 0), while it is decreasing in the interval where its derivative is negative (less than 0).
To find the interval where the function is increasing, solve the inequality f'(x)>0:
\(\begin{gathered} 6x^2-6x>0 \\ \Rightarrow6x(x-1)>0 \\ \text{ list the possible solutions:} \\ x<0,\;01 \\ Picking\text{ arbitrary numbers in the interval and checking if the inequality holds:} \\ \text{ The solution is:} \\ x<0\text{ or }x>1 \\ \Rightarrow(-$ \infty $,0)\cup(1,$ \infty $) \end{gathered}\)To find the interval where the function is decreasing, solve the inequality f'(x)<0:
\(\begin{gathered} 6x^2-6x<0 \\ \text{ Using the same procedure as the first inequality, the solution is:} \\ 0The function is increasing in the interval (-∞,0) U (1,∞).The function is decreasing in the interval (0,1).
Related Questions
A bin of 50 manufactured parts contains 3 defective parts and 47 non-defective parts. A sample of size 6 parts is selected from 50 parts. Selected parts are not replaced. How many different samples are there of size six that contain exactly 2 defective parts? What is the probability that a sample contains exactly 2 defective parts?
Answers
Answer:
535,095 different samples of size six that contain exactly 2 defective parts.
0.0337 = 3.37% probability that a sample contains exactly 2 defective parts.
Step-by-step explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
As the order of the parts is not important, the combinations formula is used to solve this question.
Combinations formula:
\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
How many different samples are there of size six that contain exactly 2 defective parts?
2 defective from a set of 3, and 4 non-defective from a set of 47. So
\(D = C_{3,2}*C_{47,4} = \frac{3!}{2!1!}*\frac{47!}{4!43!} = 535095\)
535,095 different samples of size six that contain exactly 2 defective parts.
What is the probability that a sample contains exactly 2 defective parts?
The total number of samples is:
\(T = C_{50,6} = \frac{50!}{6!44!} = 15890700\)
Then...
\(p = \frac{D}{T} = \frac{535095}{15890700} = 0.0337\)
0.0337 = 3.37% probability that a sample contains exactly 2 defective parts.
The diagram shows a circle drawn inside a square.
The circle touches the edges of the square.
12 cm
Calculate the shaded area.
Take pie to be 3.142 and write down all the digits given by your calculator.

Answers
Answer:
144 - 36×3.142 = 30.888
30.888 ÷4 = 7.722
I need help because this is a hw and I’m really confused on how to do this
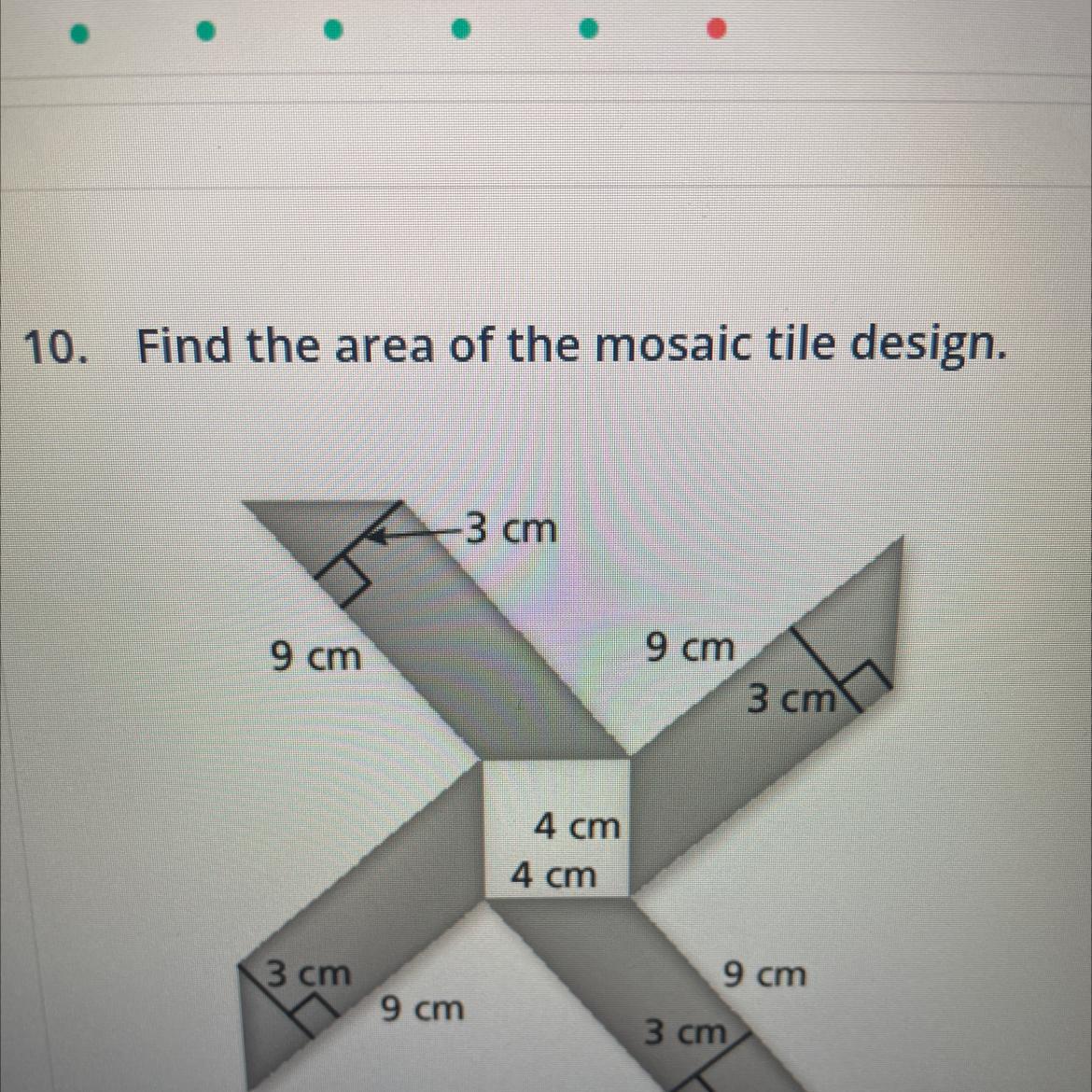
Answers
By using the formula of area of parallelogram, the area of mosaic tile design = 4x27 = 108cm^2
What is parallelogram?A parallelogram is a quadrilateral with two pairs of parallel sides. It has four sides and four angles. The opposite sides of a parallelogram are equal in length and parallel to each other. The opposite angles of a parallelogram are also equal in measure.
What is the formula to calculate the area of parallelogram?The area of a parallelogram is given by the formula:
Area = base * height
In the question there are four parallelograms, so for each the area will be
Area = 9 cm * 3 cm = 27 cm^2
for four 27x4 = 108cm^2
To learn more about parallelogram visit:
https://brainly.com/question/29147156
#SPJ1
Gary applied the distributive property using the greatest common factor to determine the expression that is equivalent to 66 + 36. His work is shown below.
Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
66 + 36 = 3 (22 + 12)
What statement best describes Gary’s error?
Gary did not use correct factors for 66 in the equation.
Gary did not use correct factors for 36 in the equation.
Gary did not use two equivalent expressions in the equation.
Gary did not use the greatest common factor in the equation.
answer this question in 5 minutes and ill give you the brainlyest and 50 points also please still answer even after the 5 minutes
Answers
The statement which best describes Gary’s error is; Gary did not use the greatest common factor in the equation.
Greatest common factorThis is the largest positive integer or polynomial that is a divisor of several different numbers. For instance, the greatest common divisor of 66, 30 and 18 is 6.
Gary's work:
66 + 36
Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
66 + 36
= 3 (22 + 12)
Gary did not use the greatest common factor in the equation.
The correct answer:
The greatest common factor of 66 and 36 is 666 + 36
= 6(11 + 6)
Therefore, Gary did not use the greatest common factor in the equation.
Learn more about greatest common factor:
https://brainly.com/question/219464
#SPJ1
138.867545518 to 4 decimal places.
Answers
Step-by-step explanation:
138 I guess I think. this is the answer.
Each of two vectors, and , lies along a coordinate axis in the xy plane. Each vector has its tail at the origin, and the dot product of the two vectors is . Which possibility is correct?
Answers
Answer:
A lies along the positive x-axis and B lies along negative x - axis .
Step-by-step explanation:
They tell us that we have two vectors, A and B. And they give us a series of conditions for this, now, what would be the correct possibility.
A lies along the positive x-axis and B lies along negative x - axis .
This is because when both vectors will be in x axis but opposite to each other, then the angle between them will be 180 ° and cos180 ° is -1.
Calculating the mean: data displays
Find the mean of the data in the bar chart below.
students
Size of each teacher's class
16
14
12
10
Number of students
8
6
4
SH
2.
0
Mr. Brehan
Mrs. Jones
Mr. Singh
Ms. Garcia

Answers
Answer:
Step-by-step explanation:
The answer is 12 students
Answer:12
Step-by-step explanation:
A portion of the quadratic formula proof is shown. Fill in the missing statement
Statements Reasons
x squared plus b over a times x plus the quantity b over 2 times a squared equals negative 4 times a times c all over 4 times a squared plus b squared over 4 a squared Find a common denominator on the right side of the equation
x squared plus b over a times x plus the quantity b over 2 times a squared equals b squared minus 4 times a times c all over 4 times a squared Add the fractions together on the right side of the equation
the quantity x plus b over 2 times a squared equals b squared minus 4 times a times c all over 4 times a squared Rewrite the perfect square trinomial on the left side of the equation as a binomial squared
x plus b over 2 times a equals plus or minus the square root of b squared minus 4 times a times c, all over 4 times a squared Take the square root of both sides of the equation
x plus b over 2 times a equals plus or minus the square root of b squared minus 4 times a times c, all over 2 times a Simplify the right side of the equation
? Subtract the quantity b over 2 times a from both sides of the equation
x equals b plus or minus the square root of b squared minus 4 times a times c, all over 2 times a
x equals negative b plus or minus the square root of b squared minus 4 times a times c, all over a
x equals negative b plus or minus the square root of b squared minus 4 times a times c, all over 2 times a
x plus b over 2 times a equals negative b plus or minus the square root of b squared minus 4 times a times c, all over 2 times a
Answers
The missing statement is the quadratic formula and the correct option therefore is the third option;
x equals negative b plus or minus the square root of b squared minus 4 times a times c, all over 2 times aWhat is the quadratic formula?The quadratic formula is used to find the solution of a quadratic equation. The quadratic formula is; \(x = \frac{-b\pm\sqrt{b^2-4\cdot a\cdot c} }{2\cdot a}\)
The statements and reasons can be presented algebraically as follows;
Statements \({}\) Reasons
\(x^2+\frac{b}{a}\cdot x+(\frac{b}{2\cdot a} )^2 = -\frac{4\cdot a\cdot c}{4\cdot a^2}+ \frac{b^2}{4\cdot a^2}\) Find a common denominator on the
right side of the equation
\(x^2 + \frac{b}{a} \cdot x+(\frac{b}{2\cdot a} )^2 = \frac{b^2-4\cdot a \cdot c}{4\cdot a^2}\) Add the fractions together on the
\({}\) right side of the equation
\((x +\frac{b}{2\cdot a} )^2 = \frac{b^2 - 4\cdot a \cdot c}{4\cdot a^2}\) Rewrite the perfect squared equation
\({}\) to the left side of the equation as a
\({}\) binomial squared
\(x + \frac{b}{2\cdot a} = \pm\sqrt{\frac{b^2 - 4\cdot a \cdot c}{4\cdot a^2} }\) Take the square root of both sides of the
\({}\) equation
\(\underline{x = \frac{-b\pm\sqrt{b^2 - 4\cdot a \cdot c} }{2\cdot a}}\) Simplify the right side of the equation
The correct option is therefore;
x equals negative b plus or minus the square root of b squared minus 4 times a times c, all over 2 times aLearn more on the quadratic formula here: https://brainly.com/question/29159682
#SPJ1
Answer:
A
Step-by-step explanation:
i took the test
have a great day :) .!
Find y. A. √22 B. 8 C. √42 D. 4

Answers
Answer:
\(\Large \boxed{\mathrm{D. \ 4}}\)
Step-by-step explanation:
The triangle is a right triangle.
We can use trigonometric functions to solve the problem.
tan θ = opp/adj
tan 30 = y/(4√3)
y = 4√3 tan 30
y = 4
what 2 plus 2 u gotta answer this right if not that is sad ok so what is 2 plus 2 use your finger thats why u got them
Answers
2 + 2 = 4
* * + * *
* * * *
Answer:
4
Step-by-step explanation:
2 + 2 is 4 cause if you add 2 two two’s it would be 4
7. A ball is dropped from a height of 80 cm. After each bounce it rebounds to 70% of its previous
maximum height.
c Find the total vertical distance travelled by the ball before it stops bouncing
d State one limitation with the model.
Answers
Through the given statement we can say that the vertical distance travelled by the ball is 84 m.
One limitation of this model is that it assumes that the ball rebounds to the same percentage of its previous maximum height after every bounce.
What is the vertical distance formula?The formula for vertical distance from the earth is y = - 1 2 g t 2 y = - frac 1 2 g t 2 y=-21gt2, where g is the acceleration of gravity and h is an elevation.
So :
C) the required total vertical distance that the given dropped ball travels until its bouncing stops:
= (12 m) + 2*(12 m)*(3/4)*[1 + 3/4 + (3/4)^2 + (3/4)^∞] [the factor 2 is for equal distance being covered up and down after each bounce of the ball]
= (12 m) + (24 m)*(3/4)*
(sum of an infinite GP series whose 1st term is 1 and common ratio is 3/4)
= (12 m) + (24 m)*(3/4)*[1/(1 - 3/4)]
= (12 m) + (24 m)*(3/4)*4
= (12 m) + (72m) = 84 m
D) This model's assumption that the ball will always bounce back to a certain proportion of its maximum height is one of its limitations. In fact, the rebound height can differ from one bounce to the next due to factors like air resistance, the ball's elasticity, and the surface it bounces on.
To know more about vertical distance visit:
brainly.com/question/4493830
#SPJ1
Ayna and Leslie both simplified the expression. Which student is correct

Answers
Given:
\(\sqrt[]{18x^4y^5}\)The expansion is,
\(\sqrt[]{18x^4y^5}=\sqrt[]{2\times3\times3\times x\times x\times x\times x\times y\times y\times y\times y\times y}\)On simplification we get,
\(\begin{gathered} =\sqrt[]{2\times3^2\times x^2\times x^2\times y^2\times y^2\times y} \\ =3x^2y^2\sqrt[]{2y} \end{gathered}\)Hence, Leslie was correct.
Let $x=5$, $y=\frac{3}{4}$, and $z=-\frac{1}{7}$. What is $$\frac{xz}{y}?$$
Answers
Answer:
-20/21Step-by-step explanation:
Given x = 5, y = 3/4 and z = -1/7, 2=we are to calculate \(\frac{xz}{y}\). Substituting the value of x, y and z into the expression will give;
\(= \frac{xz}{y}\\\\ \frac{5(-1/7)}{3/4} \\= \frac{-5/7}{3/4}\\\\= \frac{-5}{7} * \frac{4}{3}\\ \\ = \dfrac{-20}{21}\\\)
Hence the value of the expression is -20/21
explain 3 factors that should be considered in the construction of index numbers
Answers
1. selection of index number: during the construction of index number it is to be kept in mind that the selection of the index number should be correct accordingly.
2. selection of formula: while the construction of index numbers it is compulsory to select the correct formula for the given question.
3. selection of price: selection of prices should be done accordingly while constructing the index numbers.`
construction of index number is also available in two parts:
1. simple
2. weighted
1. simple: the simple method is classified into simple aggregative and simple relative.
2. weighted: the weighted method is classified into a weighted aggregative and weighted average.
read more about the construction of numbers at:
https://brainly.in/question/55819681
Convert: 83.36m= cm
pls help
Answers
Answer: 8,336
Step-by-step explanation:
So 1 meter is equal to 100 centimeters. All you have to do is multiply 83.36 by 100.
83.36 * 100 = 8,336
Hope this helps!!! :)
Given the diagram below, where and mDE = 105^ and mGE = 125^ Find m
a. 65
b. 62.5
c. 55
d. 52.5

Answers
*Complete Question:
Given the diagram below, where and mDE = 105^ and mGE = 125^ Find m<DEG
Answer:
m<DEG = 65°
Step-by-step explanation:
Angle DEG is an inscribed angle that intercepts the DG. Based on the theorem of inscribed angles, angle DEG = ½ of the measure of arc DG.
To find the measure of angle DEG, find the measure of arc DG first.
Measure of arc DG = 360° - (105° + 125°) => a full circle measures 369°
Arc DG = 360° - 230 = 130°.
m<DEG = ½ of 130° = ½*130° = 65°
Rearrange g
=
fr to make f the subject.
Answers
Answer:
f=g/rStep-by-step explanation:
divide by R
1.25 is closer to 1.04 or not ?
plz heelp
Answers
Answer:
no
Hope this helps!
mark me brailiest please
Step-by-step explanation:
what is 1 trillion to the thenth power? .. .. ..
\(\sf{}\)
Answers
1 trillion to the tenth power is (10¹⁴)¹⁰ or (10¹³)¹⁰.
What is a trillion?1,000,000,000,000One trillion is equal to one million million, or 1,000,000,000,000, and on the short scale, we write this as 1012. (ten to the twelfth power). This number is now commonly referred to as one trillion because it is a thousand times bigger than the short-scale billion.We need to determine how many crores one trillion represents. Therefore, by dividing one trillion by one crore, we can find the solution to the puzzle. As a result, we discover that 100000 = 1000000000000/10000000. As a result, we learn that $1 trillion is equivalent to 100,000 Indian Rupees.So, 1 trillion to the tenth power:
1 trillion to the tenth power = (10¹⁴)¹⁰ or (10¹³)¹⁰Therefore, 1 trillion to the tenth power is (10¹⁴)¹⁰ or (10¹³)¹⁰.
Know more about trillions here:
https://brainly.com/question/15016664
#SPJ3
The net of a cube is shown.

Answers
150 Inches... NEEERRRD
What can you say about the end behavior of the function ?A.One end decreases and one end approaches a constantB.One end increases and one end decreasesC.Both ends increaseD.Both ends decrease

Answers
ConGiven:
\(f(x)=log_2(4x+8)+16\)Required:
We need to find the end behavior of the given function.
Explanation:
Recall that the end behavior of a function f describes the behavior of the graph of the function at the "ends" of the x-axis.
Consider the graph of the given function.
\(\text{ When x}\rightarrow\infty,\text{ the function is increasing.}\)\(\text{ When x}\rightarrow-\infty,\text{ the function is undefined but decreasing.}\)Final answer:
One end increases and one end decreases

An item is regularly priced at $85. Salma bought it on sale for 35% off the regular price.
Answers
There are 40 children watching a magic show. 24 of the children are boys, and 16 of the children are girls. The magician needs to select 4 children to help him with his show. What is the probability that all 4 helpers will be girls
Answers
Answer:
1.99%. (2% rounded)
Step-by-step explanation:
The total number of ways to select 4 children out of 40 is given by the combination formula:
C(40,4) = 40! / (4! * (40-4)!) = 91,390
The number of ways to select 4 girls out of 16 is given by the combination formula as well:
C(16,4) = 16! / (4! * (16-4)!) = 1,820
Therefore, the probability of selecting 4 girls out of the group of 40 children is:
P(4 girls) = C(16,4) / C(40,4) = 1,820 / 91,390 ≈ 0.0199 or 1.99%
So the probability that all 4 helpers will be girls is approximately 1.99%
Hope this helps!.
Question 2
What is the lateral surface area of the triangular prism with the given net?
Select one:
15
9
5
12
9
9
8
8
B
8
10
Answers
Answer:
the answer is B) 24.
Step-by-step explanation:
To find the lateral surface area of the triangular prism, we need to find the perimeter of the base and then multiply it by the height of the prism.
Looking at the net, we can see that the base is a triangle with sides of length 3 cm, 4 cm, and 5 cm. So the perimeter of the base is:
3 cm + 4 cm + 5 cm = 12 cm
The height of the prism is given as 2 cm. Therefore, the lateral surface area is:
12 cm x 2 cm = 24 cm²
So the answer is B) 24.
IF THIS HELPED, CAN YOU PLEASE GIVE 5⭐? thank you
What is the slope of the following line?
A. 1/2
B. 2
C. -2
D. -1/2

Answers
Answer:
D. -1/2
Step-by-step explanation:
slope = rise/run = 1/-2 = -1/2
what number is represented by the expanded form shown? write the number in the place-value chart 70+8+6/100+3/1000

Answers
Answer:
Step-by-step explanation:
Hundreds: None
Tens: 70
Ones: 8
Tenths: None
Hundreths: 6/100
Thousandths: 3/1000
Total: 78 63/1000
Or in Numbers only:
78.063
For the question of total area of the cuboid is 200cm^.
I understand where we divide 150 by 4.
But why do I need to multiply by 5, when there are 6 faces.
Answers
You need to multiply by 5 instead of 6 because each pair of opposite faces on a cuboid has the same area, so by considering one face from each pair, you ensure that you don't count any face twice.
When calculating the total surface area of a cuboid, you need to understand the concept of face pairs.
A cuboid has six faces, but each face has a pair that is identical in size and shape.
Let's break down the reasoning behind multiplying by 5 instead of 6 in the given scenario.
To find the surface area of a cuboid, you can add up the areas of all its faces.
However, each pair of opposite faces has the same area, so you avoid double-counting by only considering one face from each pair. In this case, you have five pairs of faces:
(1) top and bottom, (2) front and back, (3) left and right, (4) left and back, and (5) right and front.
By multiplying the average area of a pair of faces by 5, you account for all the distinct face pairs.
Essentially, you are considering one face from each pair and then summing their areas.
Since all the pairs have the same area, multiplying the average area by 5 gives you the total surface area.
When dividing 150 by 4 (to find the average area of a pair of faces), you are essentially finding the area of a single face.
Then, by multiplying this average area by 5, you ensure that you account for all five pairs of faces, providing the total surface area of the cuboid.
Thus, multiplying by 5 is necessary to correctly calculate the total surface area of the cuboid by accounting for the face pairs while avoiding double-counting.
For similar question on cuboid.
https://brainly.com/question/29568631
#SPJ8
PLS HELP ME ASAP !!!

Answers
The probability that she picks a blue marble three times in a row is 1/125.
Given that
Samantha has a bag of 5 different colored marbles.
She randomly picks a marble from the bag, records the color, and returns it to the bag before picking another marble.
We have to determine
What is the probability that she picks a blue marble three times in a row?
According to the question
Samantha has a bag of 5 different colored marbles.
She randomly picks a marble from the bag, records the color, and returns it to the bag before picking another marble.
The probability of picking a bag one time is,
Number of bag pack at a time
Total number of bag
=1/5
The probability of picking a bag second time is,
Number of bag pack at a time Total number of bag
=1/5
The probability of picking a bag third time is,
Number of bag pack at a time
Total number of bag
=1/5
031%
Therefore,
The probability that she picks a blue marble three times in a row is,
= 1/5 X 1/5 X 1/5
1 /125
Hence, the probability that she picks a blue marble three times in a row is 1/125.
To know more about Probability click the link given below.
https://brainly.com/question/11441437
Step-by-step explanation:
hope this helps
The woodwind section of the middle school band makes up 1/4 of the band. There are 9 members in the woodwind section. Use the equation 1/4m= 9 to find the number of members (m) in the band.
Answers
Answer:
36 members
Step-by-step explanation:
Given that:
Woodwind section = 1/4 of the total band
Members if woodwind section = 9
Total members of band (m) :
1/4 * m = 9
m/4 = 9
Multiply both sides by 4
m/4 * 4 = 9 * 4
m = 36
Total band members = 36
How many decimal places are in the product of the expression below?
256
x142
one
two
three
four
Answers
Answer:
36352.0
Step-by-step explanation:
For 256x142 = 36352.0
There is none actually