Please solve this for me

The total amount it costs Jeff and Valerie to fill up their vehicles.

The correct option is D.

bx is most likely the amount it costs Jeff and Valerie to fill up their cars because they both pay x dollars per gallon.

Ay = Megan Bx

= Valerie and Jeff

Ay + Bx = Megan + Valerie and Jeff

Algebra is a field of mathematics that assists in the depiction of problems or situations using mathematical expressions. To produce a meaningful mathematical expression, variables like as x, y, and z are used, as well as mathematical operations such as addition, subtraction, multiplication, and division.

Working from left to right, first complete multiplication and division, then addition and subtraction.

The principles of algebra include numbers, variables, constants, expressions, equations, linear equations, as well as quadratic equations.. It also includes basic mathematical operations such as addition, subtraction, multiplication, and division within algebraic equations.

To know more about Algebra visit:

https://brainly.com/question/24875240

#SPJ9

To find a vector v orthogonal to the plane through the points p(4, 0, 0), q(0, 3, 0), and r(0, 0, 5), we can use the cross product of two vectors that lie in the plane.

Let's first find two vectors that lie in the plane. We can take the vectors p to q and p to r.

Vector p to q can be calculated as q - p, which is (0 - 4, 3 - 0, 0 - 0) = (-4, 3, 0).

Vector p to r can be calculated as r - p, which is (0 - 4, 0 - 0, 5 - 0) = (-4, 0, 5).

Now, we can find the cross product of these two vectors.

To calculate the cross product, we take the determinant of a 3x3 matrix.

The cross product is given by:

(i  j  k)
(-4  3  0)
(-4  0  5)

Using the determinant formula, we get:

(3 * 5 - 0 * 0)i - (-4 * 5 - 0 * -4)j + (-4 * 0 - 3 * -4)k

Simplifying, we have:

15i - (-20)j - (-12)k

Which gives us:

15i + 20j - 12k

Therefore, a vector v orthogonal to the plane through the points p, q, and r is given by 15i + 20j - 12k.

vector v and orthogonal to the plane : https://brainly.com/question/14527445

#SPJ11

Answer:

-3(2x+3)=21 does not become -6x+9=21 because wrong foiling.

Step-by-step explanation:

When you distribute -3 with 2x+3 you multiply both values by -3.

-3*2x = -6x

-3*3 = -9 <- This is where the error is. It's -9, not +9.

It will take Rick 15 weeks to reach his target weight of 175 pounds.

Let "w" represent the number of weeks it will take for Rick to reach his target weight.

The rate at which Rick is losing weight is 2 pounds per week, so the amount of weight he will lose in "w" weeks can be represented as 2w.

The equation to represent the weight loss can be written as 205 - 2w = 175, where 205 is Rick's current weight and 175 is his target weight.

Solving the equation, we subtract 205 from both sides and divide by 2: -2w = -30, w = 15.

learn more about:- linear equation  here

https://brainly.com/question/12974594

#SPJ11

The regression equation for this data is Y = 1.5X - 36.5. The predicted value of Y when X = 27 is 29.

We can use the Excel LINEST function to calculate the regression equation for this data. The LINEST function takes the following arguments:

The output of the LINEST function is an array of coefficients, which can be used to calculate the regression equation. In this case, the coefficients are:

b0 = -36.5

b1 = 1.5

The regression equation is therefore:

Y = b0 + b1X

= -36.5 + 1.5X

To predict the value of Y when X = 27, we can simply substitute this value into the regression equation. This gives us:

Y = -36.5 + 1.5 * 27

= 29

Therefore, the predicted value of Y when X = 27 is 29.

To know more about coefficient click here

brainly.com/question/30524977

#SPJ11

Answer:

The value of c is 2

Step-by-step explanation:

p(x) = cx³ - 15x - 68

Since it's divisible by ( x - 4) that means when the value of ( x - 4) is substituted into the polynomial it leaves a remainder of zero that's no remainder.

x - 4 = 0

x = 4

Substitute it into the above expression

That's

c(4)³ - 15(4) - 68 = 0

64c - 60 - 68 = 0

64c = 60 + 68

64c = 128

Divide both sides by 64

c = 2

Hope this helps you

Answer:

h

Step-by-step explanation:

b

Transfer function of the system is:X(s)/Y(s) = 10/(s^2+1.6s+4)We need to find the following:

a) Y(t); b) Percent overshoot; c) Ultimate value of Y(t); d) Maximum value of Y(t) and e) Period of oscillation.

(a) Calculation of Y(t):The transfer function of the system isX(s)/Y(s) = 10/(s^2+1.6s+4)Now, applying the Laplace inverse on both sides,Y(s) = 10/(s^2+1.6s+4) × X(s)Taking the inverse Laplace of Y(s),y(t) = L^-1 {10/(s^2+1.6s+4) × X(s)}Using partial fraction decomposition to find the inverse Laplace of Y(s), we get:y(t) = 1.2508{ 2.22 e^(-0.8t) - 0.22 e^(-3.2t)}Therefore, the value of Y(t) is 1.2508{ 2.22 e^(-0.8t) - 0.22 e^(-3.2t)}.

(b) Calculation of percent overshoot:The transfer function of the system isX(s)/Y(s) = 10/(s^2+1.6s+4)The damping ratio (ζ) can be given asζ = 1/2 √(ζ²-4)ζ = 1/2 √(1.6²-4)ζ = 0.6For a second-order system with a damping ratio of 0.6, the percent overshoot is given as:%OS = e^(-ζπ/√(1-ζ²)) × 100%OS = e^(-0.6π/√(1-0.6²)) × 100OS = 26.12%Hence, the percent overshoot is 26.12%.

(c) Calculation of the ultimate value of Y(t):The transfer function of the system isX(s)/Y(s) = 10/(s^2+1.6s+4)For the ultimate value of Y(t), we take the limit of sY(s) as s tends to 0.The value of Y(s) is given as:Y(s) = 10/(s^2+1.6s+4) × X(s)On simplifying the above equation, we get:sY(s) + 1.6 Y(s) + 4 Y(s) = 10 X(s)Now, taking the limit of sY(s) as s approaches 0,sY(s) = lim s→0 sY(s) = 0Therefore, 1.6 Y(s) + 4 Y(s) = 10 X(s)Taking the limit of Y(s) as s approaches 0,0 = 10 X(0)Y(0) = 2.5Hence, the ultimate value of Y(t) is 2.5.

(d) Calculation of the maximum value of Y(t):The maximum value of Y(t) is given as:Ymax = 2.5 + (1+ζ²)^0.5 e^(-ζπ/√(1-ζ²)) / (ζ√(1-ζ²))The value of ζ is 0.6Hence, substituting the value of ζ in the above equation, we get:Ymax = 2.5 + (1+0.6²)^0.5 e^(-0.6π/√(1-0.6²)) / (0.6√(1-0.6²))Ymax = 3.129

(e) Calculation of the period of oscillation: The period of oscillation is given as:T = 2π / ωnWhere,ωn = √(1-ζ²) / (2ζ)Therefore,ωn = √(1-0.6²) / (2 × 0.6)ωn = 1.302Therefore,T = 2π / ωnT = 4.830sHence, the period of oscillation is 4.830s.

period of oscillation: https://brainly.com/question/29813582

#SPJ11

The total number of possible words is 155.

How many words are possible? (A word can use a letter more than once, but 0 letters do not count as a word)

There are 5 letters in the mumblian alphabet, and each word must contain 1, 2, or 3 letters.

The number of 1 letter words is 5 since every letter is a word.

The number of 2 letter words is 5 × 5 = 25 because there are 5 options for the first letter and 5 options for the second letter.

The number of 3 letter words is 5 × 5 × 5 = 125 because there are 5 options for the first letter, 5 options for the second letter, and 5 options for the third letter. Therefore, the total number of possible words is:

\($5 + 25 + 125 = \boxed{155}$\)

To know more about letter words problems: https://brainly.com/question/29424977

#SPJ11

Using the area formula for a rectangle and considering the geometric properties of a trapezoid, we have derived the formula for finding the area of a trapezoid.

The formula for the area of a trapezoid can be derived by using the area formula for a rectangle and some mathematical properties.

Let's consider a trapezoid with bases of lengths b1 and b2, and a height h. To find the area of the trapezoid, we can break it down into two parts: a rectangle and two right triangles.

Start by drawing a straight line parallel to the bases of the trapezoid to create a rectangle.

The length of the rectangle is the average of the lengths of the two bases: (b1 + b2) / 2.

The width of the rectangle is equal to the height of the trapezoid: h.

The area of the rectangle is given by the formula: Area_rectangle = length * width = ((b1 + b2) / 2) * h.

Now, we need to subtract the areas of the two right triangles formed outside the rectangle.

Each right triangle has a base equal to the difference between one of the trapezoid bases and the length of the rectangle: (b1 - ((b1 + b2) / 2)) and (b2 - ((b1 + b2) / 2)).

The height of each right triangle is equal to the height of the trapezoid: h.

The area of a right triangle is given by the formula: Area_triangle = (base * height) / 2.

Therefore, the combined area of the two right triangles is: 2 * [(b1 - ((b1 + b2) / 2)) * h / 2].

Simplifying the expression: (b1 - ((b1 + b2) / 2)) * h = (b1 - b1/2 - b2/2) * h = (b1/2 - b2/2) * h = ((b1 - b2) / 2) * h.

Adding the area of the rectangle and subtracting the combined area of the two right triangles, we get the formula for the area of the trapezoid:

Area_trapezoid = ((b1 + b2) / 2) * h - ((b1 - b2) / 2) * h.

Simplifying further, we can factor out the common factor of h:

Area_trapezoid = (b1 + b2 - (b1 - b2)) * h / 2.

Finally, simplifying the expression within the parentheses:

Area_trapezoid = (2b2) * h / 2.

This simplifies to the formula for the area of a trapezoid:

Area_trapezoid = (b1 + b2) * h / 2.

Therefore, using the area formula for a rectangle and considering the geometric properties of a trapezoid, we have derived the formula for finding the area of a trapezoid.

for such more question on rectangle

https://brainly.com/question/17297081

#SPJ11

The side lengths of the real object will be 50 inches and 60 inches.

The scale factor is the ratio of the actual size of the image to the new size of the image. It is used to Map the objects like if you want to increase or decrease the size without changing the original shape of the image it is done by the scale factor.

The given scale factor is 5:1, which means that the dimensions of the scale drawing are 1/5 of the dimensions of the real object.

To find the side lengths of the real object, we can use the ratio of the dimensions in the scale drawing and the real object.

For example, the length of the real object can be found by multiplying the length of the scale drawing by the scale factor:

Real object length = Scale drawing length x Scale factor

Real object length = 10 in x 5

Real object length = 50 in

Similarly, the width of the real object can be found using the same method:

Real object width = Scale drawing width x Scale factor

Real object width = 12 in x 5

Real object width = 60 in

Therefore, the side lengths of the real object are 50 inches and 60 inches.

To know more about scale factors follow

brainly.com/question/2826496

#SPJ9

Answer:

10m

10m

Step-by-step explanation:

Answer:

area of a rectangle can be used to find the basketball court's area

area of rectangle = length* width

area of court = 29m*15m = 435 square metres.

Answer:

10, 80 and 90 degrees.

Step-by-step explanation:

The third angle will  90 - 10 = 80 degrees.

Answer: 5:7, 5 to 7, 5/7

Step-by-step explanation:

Since the ratio is the number of red roses to total, you must add 5 and 2 to get the total. The ratio is 5 to 7.

These are three ways to write a ratio:

1. Using the colon symbol

5:7

2. Using the word to

5 to 7

3. As a fraction

5/7

The truth table represents statements p, q, and r. The correct options statements  are:

1. p ↔ q

3. q ↔ p

4. q ↔ r

For option 1. p ↔ q, This term is the biconditional statement "p is true if and only if q is true", and it is only valid when the truth values of p and q are identical. To put it differently, the truth values of p and q are identical, either being true or false.

For option 2 q ↔ p,  is one that is as identical as the biconditional is symmetrical. In other words, q ↔ p has the same logical equivalence as p ↔ q.

Learn more about truth table  from

https://brainly.com/question/10607091

#SPJ1

Answer:

Step-by-step explanation:

Given data:

Put this into ascending order:

Median is 6 as both middle numbers are same = 6

Split the data into lower and upper halves:

Q1 is the median of the lower half:

Q3 is the median of the upper half:

IQR is the difference of Q3 and Q1

The domain of the function f(x) = ∛x + 2 is all real numbers such that x ≥ 0. This is because the cube root function is defined only for non-negative numbers.

What do a function example's range and domain mean?

A straightforward function, such as f(x) = x2, can have a domain (what goes in) of just the counting numbers 1, 2, 3, etc., and a range (what comes out) of the set 1, 4, 9, etc. Another function, g(x) = x2, may have an integer domain of..., -3, -2, -1, 0... 1, 2, 3, and its range is..., 1, 4, 9,...

For the range, the function f(x) = ∛x + 2 is a monotonically increasing function over the domain, which means that it increases as the input x increases. Therefore the range of f(x) = ∛x + 2 is all real numbers greater than or equal to 2

So the domain is x>=0 and the range is y>=2

learn more about range and domain

https://brainly.com/question/26098895

#SPJ1

James will fully clear the loan after approximately 12 years when the remaining balance reaches zero.

To determine the number of years it will take for James to fully clear the loan, we need to calculate the remaining balance after each payment and divide the initial loan amount by the annual payment until the remaining balance reaches zero.

The loan amount is 9000 euros, and James pays off 770 euros each year. Since the interest is charged at a rate of 3% of the original amount per annum, the interest for each year will be \(0.03 \times 9000 = 270\) euros.

In the first year, James pays off 770 euros, and the interest on the remaining balance of 9000 - 770 = 8230 euros is \(8230 \times 0.03 = 246.9\)euros. Therefore, the remaining balance after the first year is 8230 + 246.9 = 8476.9 euros.

In the second year, James again pays off 770 euros, and the interest on the remaining balance of 8476.9 - 770 = 7706.9 euros is \(7706.9 \times 0.03 = 231.21\) euros. The remaining balance after the second year is 7706.9 + 231.21 = 7938.11 euros.

This process continues until the remaining balance reaches zero. We can set up the equation \((9000 - x) + 0.03 \times (9000 - x) = x\), where x represents the remaining balance.

Simplifying the equation, we get 9000 - x + 270 - 0.03x = x.

Combining like terms, we have 9000 + 270 = 1.04x.

Solving for x, we find x = 9270 / 1.04 = 8913.46 euros.

For more such questions on loan

https://brainly.com/question/25696681

#SPJ8

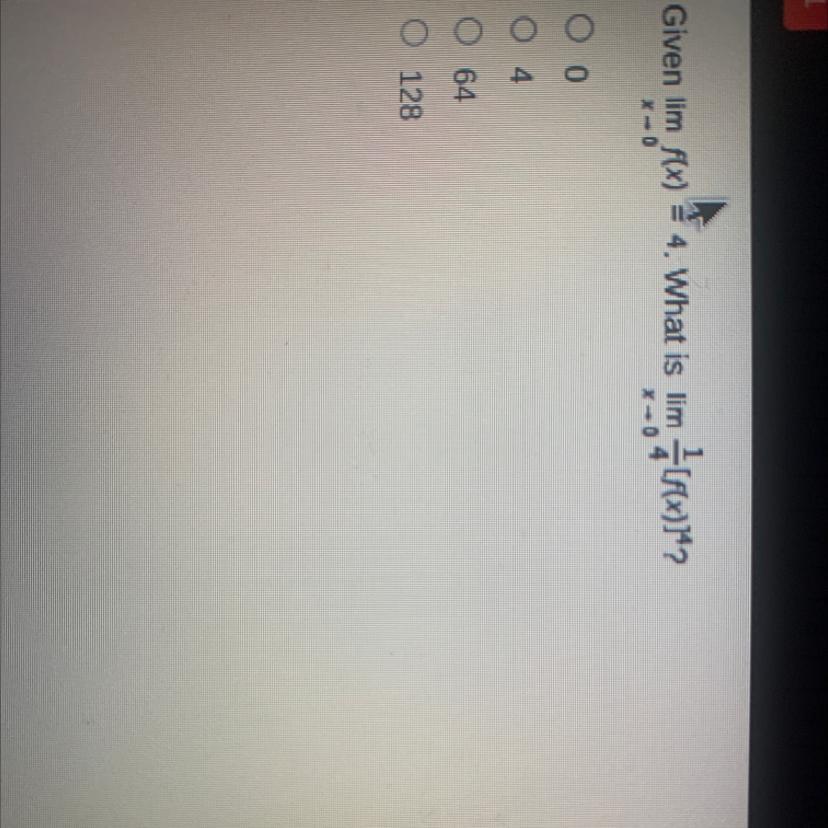
The value of the wanted limit is:

\(\lim_{x \to 0} \frac{1}{4} (f(x))^4 = 64\)

So the correct option is the third one.

Here we know that:

\(\lim_{x \to 0} f(x) = 4\)

And we want to find the value of the limit:

\(\lim_{x \to 0} \frac{1}{4} (f(x))^4\)

Notice that because neither the fraction nor the power depend on the value of x, we can put the limit inside the parenthesis to get:

\(\lim_{x \to 0} \frac{1}{4} (f(x))^4 = \frac{1}{4} (\lim_{x \to 0} f(x))^4\)

And we know that the thing inside the parenthesis is 4, then:

\(\frac{1}{4} (\lim_{x \to 0} f(x))^4 = \frac{1}{4} (4)^4 = 4^3 = 64\)

Learn more about limits at:

https://brainly.com/question/5313449

#SPJ1

Negative numbers get smaller the more they move away from 0.

Answer:

-15

Step-by-step explanation:

The greater the number after the minus sign, the smaller it is.

For example, -5 is smaller than -1.

Given a function f(x,y) of two variables with the point (20,10) is a critical point, but it is not a local extremum.

According to the given information:

f(x = 20,y = 10)Let f_x(x,y) and f_y(x,y) be the partial derivatives of f(x,y) with respect to x and y, respectively.

\(f_x(x,y) = f(x,y)\\dx/dt|_y=yf_y(x,y) \\\= f(x,y)dy/dt|_x=xAt (x=20,y=10), f_x(20,10) = 0, \\f_y(20,10) = 0.\)

Thus, (20,10) is a critical point of f(x,y) or stationary point.  Now, let f_xx, f_yy, and f_xy be the second-order partial derivatives of f(x,y) at (x,y).f_xx(x,y) = d^2f/dx^2|_y=yf_yy(x,y) = d^2f/dy^2|_x=xf_xy(x,y) = d^2f/dxdy|_x=xf_xx(20,10) = -2, f_yy(20,10) = -5 and f_xy(20,10) = 3. The Hessian matrix of f at (20,10) is given by:

Hessian(f)(20,10) = \([f_xx(20,10) f_xy(20,10); f_xy(20,10) f_yy(20,10)] = [-2 3; 3 -5]\)

The discriminant of the Hessian matrix is given by \(D = f_xx(x,y)f_yy(x,y) - f_xy(x,y)^2\)

Here, D = (-2)(-5) - (3)^2 = 4 > 0Since D > 0 and f_xx(20,10) < 0, the point (20,10) is a saddle point. Therefore, the point (20,10) is a critical point but it is not a local extremum.

Hence, the answer is: Yes, the point (20,10) is a critical point, but it is not a local extremum.

To know more about critical points, visit:

https://brainly.com/question/32077588

#SPJ11

Answer:

241/35 = 6  31/35

Step-by-step explanation:

2  3/5 + 4  2/7 = 241/35

As a result of answering the given question, we may state that As a cylinder result, the figure's volume is roughly 365.69 cubic units.

A cylinder is a three-dimensional geometric object composed of two congruent parallel circular bases and a curving surface connecting the two bases. A cylinder's bases are always perpendicular to its axis, which is an imaginary straight line through the centre of both bases.  A cylinder's volume is equal to the product of its base area and height. The volume of a cylinder is calculated as V = r2h, where "V" represents the volume, "r" represents the radius of the base, and "h" represents the cylinder's height.

V = l × w × h

When we substitute the provided values, we get:

V = 10* 6* 4 = 240 cubic metres

The cylinder has a radius of three and a height of four. The volume of a cylinder volume is given by the following formula:

\(V = πr^2h\)

V = 32 x 4 = 36 cubic units

V = 1/3 × B × h

The base has the following area:

B = l w = 6 4 = 24 units square

When we substitute the provided values, we get:

V = 1/3 24 3 = 8 cubic metres

Total Volume = 240 + 36 + 8 365.69 cubic units = Rectangular Prism Volume + Cylinder Volume + Pyramid Volume (rounded to two decimal places)

As a result, the figure's volume is roughly 365.69 cubic units.

To know more about cylinder visit:

https://brainly.com/question/16134180

#SPJ1

Answer:

70

Step-by-step explanation:

The first term on the left-hand side represents the flux of the quantity D(pu δ) across the cell boundaries, and the second term represents the change of this flux within the cell.

To integrate the 1D steady-state convection-diffusion equation over a typical cell, we can start with the given equation:

D/dx(pu δ) = d/dx (rd δ/dx)

Here, D is the diffusion coefficient, p is the velocity, r is the reaction term, u is the concentration, and δ represents the Dirac delta function.

To integrate this equation over a typical cell, we need to define the limits of the cell. Let's assume the cell extends from x_i to x_i+1, where x_i and x_i+1 are the boundaries of the cell.

Integrating the left-hand side of the equation over the cell, we have:

∫[x_i to x_i+1] D/dx(pu δ) dx = D∫[x_i to x_i+1] d(pu δ)/dx dx

Using the integration by parts technique, the integral can be written as:

= [D(pu δ)]_[x_i to x_i+1] - ∫[x_i to x_i+1] d(D(pu δ))/dx dx

Similarly, integrating the right-hand side of the equation over the cell, we have:

∫[x_i to x_i+1] d/dx (rd δ/dx) dx = [rd δ/dx]_[x_i to x_i+1]

Combining the integrals, we get:

[D(pu δ)][x_i to x_i+1] - ∫[x_i to x_i+1] d(D(pu δ))/dx dx = [rd δ/dx][x_i to x_i+1]

This equation can be further simplified and manipulated using appropriate boundary conditions and assumptions based on the specific problem at hand.

To know more about integrate refer to-

https://brainly.com/question/31744185

#SPJ11

The statements true are B)The data is best represented by a quadratic model. and C) If the price is $5 per unit, the expected profit is approximately $4,686.

We have the Information regarding the data is given below

Expected profit is the probability of receiving a certain profit times the profit, and the expected cost is the probability that a certain cost will be incurred times the cost.

The data should be best presented by  the quadractic model.

In the case when the price should be $5 per unit so the profit should be $4,686.

Therefore,option B and option C these two options are correct.

Theefore the  true  statements are,The data is best represented by a quadratic model. and If the price is $5 per unit, the expected profit is approximately $4,686.

To learn more about the expected profit visit:

https://brainly.com/question/24778422

Answer:

b,c

Step-by-step explanation:

trust

The mathematical expression y(x,t) = Asin(kx)sin(wt) provides a way to describe the behavior of a standing wave in terms of its amplitude, frequency, and location along the string.

At time t=0,

the standing wave can be mathematically expressed as

y(x,0) = Asin(kx)sin(w*0) = Asin(kx)sin(0) = 0.

This means that the displacement of the string is zero at time t=0.

However, it is important to note that this does not mean that the string is not moving at all. Rather, it means that the string is in a state of equilibrium at time t=0, with the maximum transverse displacement being A.

As time progresses, the standing wave will oscillate between the maximum positive and negative transverse displacement values, creating a pattern of nodes (points of zero displacements) and antinodes (points of maximum displacement).

The wave number k and angular frequency w are both constants that are dependent on the physical properties of the string and the conditions under which the wave is being produced.

To learn more about Expression :

https://brainly.com/question/1859113

#SPJ11

The odd cubic function f(x) = x³ - 4x² + 5 is approaching (x → ∞, y → ∞).

A polynomial function's final behavior is how its graph behaves as x gets closer to positive or negative infinity.

The graph's final behavior is determined by a polynomial function's degree and leading coefficient.

The function f(x) = x³ - 4x² + 5 is an odd cubic function that is symmetric about the origin.

As x approaches negative infinity the function f(x) also approaches negative infinity but at a faster rate and as approaches positive infinity the function f(x) also approaches positive infinity at a faster rate.

learn more about end behavior of a polynomial here :

https://brainly.com/question/29255299

#SPJ1