Please help
If the dimensions of a Cooler is 24 inches long, 14 1/2 inches wide, and 12 inches deep, What is Volume of the Cooler?
Answers
Answer:
volume is 4,176 in cubed
Step-by-step explanation:
hope this helps
24 x 14.5 x 12 = 4,176
Answer:
4,176 in³Step-by-step explanation:
The formula for finding the volume of a rectangular prism, which is the type of solid a cooler is length times width times height.
a = lwh
Substituting, we get:
a = 24 x 14 1/2 x 12
24 x 12 = 288
288 x 14.5 = 4,176
We also must express our answer in cubic inches (in³)
Answer is 4,176 in³
Related Questions
based on the graph how many tiles are im figure 0

Answers
For figure {0}, the number of tiles will be equal to 2.
What is a mathematical function, equation and expression?Function : In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function
Expression : A mathematical expression is made up of terms (constants and variables) separated by mathematical operators
Equation : A mathematical equation is used to equate two expressions.
Given is a graph as shown in the image.
The line passes through point -
(3, 8) and (4, 10)
So, the slope of the line will be -
m = (10 - 8)/(4 - 3)
m = 2
y = 2x + c
For the point (3, 8), we can write -
8 = 6 + c
c = 2
For figure {0}, the number of tiles will be equal to 2.
Therefore, for figure {0}, the number of tiles will be equal to 2.
To solve more questions on functions, expressions and polynomials, visit the link below -
brainly.com/question/17421223
#SPJ1
Which expression has a negative value?
−5⋅5⋅−5⋅−5⋅−5
−5⋅5⋅−5⋅−5
−5⋅−5⋅5
−5⋅−5
Answers
Answer: The answer would be B
Step-by-step explanation:
I had a test like this so I kinda know wut the answer is a few weeks or so ago but u need to multiply -5 • 5 (which would be negative since it has one negative sign) then multiply -5 • -5 (since it has another negative it’s positive) then u just multiply the answers that u got from the times 5 u did -bonus if it’s 1 negatives it’s a negative but if it’s 2 negatives it’s a positive
Answer:
The answer is B
Step-by-step explanation:
help me asap please on this math question

Answers
Equations showing direct variations are 2x = y and y = 1.8c
Direct Variation exists between two variables when one variable is directly dependent to another variable means change in one variable will create change in other one also and vice versa.
Two variable increase or decrease by the same factor.
Suppose x and y is that are in direct variation then you can write
y ∝ x
where, "∝" denotes proportionality
removing proportionality sign by constant then you can write
y = k x , where k is constant and can hold any real value
From the following equation ,
2x = y with 2 as constant and
y = 1.8x with 1.8 as constant shows direct variations
To know more about Direct variation here
https://brainly.com/question/18087321
#SPJ1
NEED HELP ASAP The equation of line a is: -x + 4y = 32
How do theses equations compare to line a?
y=1/4x + 1
-4x+y=-8
4x+y=-3

Answers
y = 1/4x + 1 is parallel to line a
-4x + y = -8 is neither parallel nor perpendicular to line a
4x + y = -3 is perpendicular to line a
Parallel and Perpendicular linesFrom the question, we are to determine how the given equations compare to line a.
From the given information,
Line a is -x + 4y = 32
First, we will determine the slope of line a
To do this, we will compare the equation to the slope-intercept form of a line
The slope-intercept form of a line is
y = mx + b
Where m is the slope
and b is the y-intercept
Writing -x + 4y = 32 in the slope-intercept form
-x + 4y = 32
4y = x + 32
Divide through by
y = 1/4 x + 8
By comparison, the slope of line a is 1/4
NOTE: If two lines are parallel, their slopes will be equal
and
If two lines are perpendicular, their slopes will be the negative reciprocal of each other
Now, we will determine the slopes of each of the lines
For y = 1/4x + 1
By comparing with the slope-intercept form of a line, y = mx + b
The slope of the line is 1/4
Thus, the line is parallel to line a
For -4x+y=-8
Rewrite in the slope-intercept form of a line
-4x + y = -8
y = 4x - 8
By comparing with the slope-intercept form of a line, y = mx + b
The slope of the line is 4
4 is not equal to 1/4 and 4 is not the negative reciprocal of 1/4.
Thus, the line is neither parallel nor perpendicular to line a.
For 4x+y=-3
Rewrite in the slope-intercept form of a line
4x + y = -3
y = -4x - 3
By comparing with the slope-intercept of a line, y = mx + b
The slope of the line is -4
-4 is the negative reciprocal of 1/4.
Thus, the line is perpendicular to line a.
Learn more on Parallel and Perpendicular lines here: https://brainly.com/question/7396586
#SPJ1
Can yall hel me with this pls

Answers
Answer:
X = 10
Z = 67
Step-by-step explanation:
We see that the angles are formed by the intersection of two lines.
Angles z and 67° are vertically opposite angles and therefore they are equal to each other
z°= 67°
Angles z and (7x + 43) are supplementary angles. The sum of these angles add up to 180°
z + 7x + 43 = 180
67 + 7x + 43 = 180
7x + 110 = 180
7x = 180 -110 = 70
x = 70/7 = 10
can someone please help

Answers
Answer:
The measure of CD is 46
Step-by-step explanation:
From the midpoint theorem, we have,
FG = (1/2)CD
so,
\(13+5x=(1/2)(-3x+52)\\So,\\2(13+5x)=-3x+52\\26+10x=-3x+52\\13x=52-26\\13x=26\\x=26/13\\x=2\)
Now,
\(CD = -3x+52\\since \ x=2\\we \ get\\CD=-3(2) +52\\CD=-6+52\\CD=46\)
What are the zeros of f(x) = x(x-7)?
A. x = 0 and x = -7 O
B. x = 0 only ооо O
c. x = 0 and x = 7
D. X = 7 only
Answers
Answer:
c. 0 and 7
Step-by-step explanation:
A confidence interval that includes the null hypothesis may still result in a statistically significant difference or association.
Answers
Even with the null hypothesis included in the confidence interval, there might be a statistically significant difference or correlation.
Describe the term confidence interval?An estimate's level of uncertainty is indicated by a confidence interval, which is a range of numbers. A confidence interval is denoted by its endpoints.
Confidence intervals are commonly employed by statisticians to gauge the degree of uncertainty in either a sample variable. For instance, to determine how each sample might accurately reflect the true value of a population variable, a researcher chooses many samples at random taken from the same population as well as computes the confidence interval for each sample.A confidence interval is a set of values that are likely to contain an unidentified population parameter and are bound across each statistic's mean. According to statistical significance, there is a strong possibility that our conclusion that two variables are related is accurate.Thus, even with the null hypothesis included in the confidence interval, there might be a statistically significant difference or correlation.
To know more about the confidence interval, here
https://brainly.com/question/15712887
#SPJ4
The complete question is-
A confidence interval that includes the null hypothesis may still result in a statistically significant difference or association. (True /False).
Which value of x in the equation 18x + 5 - 3 = 65 makes the equation true
Answers
Answer:
the value of x that makes the equation true is x = 3.5.
Step-by-step explanation:
To find the value of x that makes the equation 18x + 5 - 3 = 65 true, we need to simplify the equation and solve for x.
Starting with the equation:
18x + 5 - 3 = 65
First, combine like terms:
18x + 2 = 65
Next, isolate the term with x by subtracting 2 from both sides:
18x = 65 - 2
18x = 63
Finally, divide both sides of the equation by 18 to solve for x:
x = 63 / 18
x = 3.5
Therefore, the value of x that makes the equation true is x = 3.5.
The answer is:
x = 7/2 (3.5 in decimal form)Steps & work :
First, I focus only on the left side.
Combine like terms:
\(\sf{18x+5-3=65}\)
\(\sf{18x+2=65}\)
Subtract 2 from each side:
\(\sf{18x=63}\)
Now, divide each side by 18:
\(\sf{x=\dfrac{63}{18}\)
Clearly, this fraction is not in its simplest terms, and we can divide the top and bottom by 9:
\(\sf{x=\dfrac{7}{2}}\)
\(\therefore\:\:\:\:\:\:\stackrel{\bf{answer}}{\boxed{\boxed{\tt{x=\frac{7}{2}}}}}}\)
The equation m=3b represents the times in minutes (m) it takes a chef to cook a certain number of bacon cheeseburgers (b) A: 3 B: 6 C:1/3 D: 1
Answers
For the given equation:
m = 3b
The constant of proportionality is 3, so the correct option is A.
How to determine the constant of proportionality?
After a small search on the internet, I've found that this question asks for the constant of proportionality.
Remember that a proportional relation is of the form:
y = k*x
Where k is the constant of proportionality, and x and y are the variables.
Here the relation is:
m = 3*b
Where m and b are the variables, then the remaining coefficient is the constant of proportionality, which is 3.
In this way, we can see that the correct option is A.
Learn more about proportional relationships:
https://brainly.com/question/12242745
#SPJ1
what is 453,605 rounded to the nearest thousand
Answers
Answer:
453605 rounded to the nearest thousand is 454000
2. Given the situations below, Identify if it is a linear or exponential model or neither.
Explain your reasoning.
a. A savings account that starts with $5000 and receives a deposit of $825 per month.
Answers
Step-by-step explanation:
The situation described can be modeled using a linear equation, where the balance of the savings account increases by a fixed amount every month. Specifically, the equation that represents this situation is:
balance = $5000 + $825 * months
where "months" represents the number of months that have passed since the account was opened. The slope of this line is constant at $825, indicating that the balance is increasing by the same amount every month.
Therefore, the model for this situation is linear.
Simplify the following algebraic expression.
square root of 392x^7
Answers
Answer:
\( \sqrt{392 {x}^{7} } \)
Simplify
that's
\( \sqrt{392} \times \sqrt{ {x}^{7} } \\ \\ = \sqrt{196 \times 2} \: \times \sqrt{ {x}^{7} } \\ \\ = 14 \sqrt{2} \times \sqrt{ {x}^{7} } \\ \\ = 14 \sqrt{2x ^{7} } \)
Hope this helps you
Michaela plans on installing heated tile in her kitchen. A diagram of the kitchen floor plan is shown below.
Calculate the area of the floor, to the nearest 10th, to determine how many square metres of tile Michaela will need to buy.
*Hint: Divide the shape into 2! You will need to use trig!

Answers
Check the picture below.
so hmm we have a 6x6 square atop and a triangle with base of 6 and a height of "h", let's get "h".
\(\sin( 42^o )=\cfrac{\stackrel{opposite}{h}}{\underset{hypotenuse}{2}} \implies 2\sin(42^o)=h \implies 1.34\approx h \\\\[-0.35em] ~\dotfill\\\\ \stackrel{ \textit{\LARGE Areas} }{\stackrel{triangle}{\cfrac{1}{2}(\underset{b}{6})(\underset{h}{1.34})}~~ + ~~\stackrel{ square }{(6)(6)}} ~~ \approx ~~ 4.02+36~~ \approx ~~ \text{\LARGE 40.0}\)

I don't know how to ask a question here so can I just send you a picture?

Answers
the circle is in the third quadrant and its coordinate of the centre is,
Q(-4,-5)
now after the translation of the circle into first quadrant,
its coordinate of the centre will be Q' (4,5)
thus, the equation of the translation is,
Q(x,y) ---> Q' (-x , - y)
thus, the correct answer is option C
(x,y) ----> (-x, -y))
9 is subtracted from the square of a number
Answers
A student in wildlife management studied trout habitat in the upper Shavers Fork watershed in West Virginia. The springtime water pH of 29 randomly selected tributary sample sites were found to have the following values:
6.2 6.3 5.0 5.8 4.6 4.7 4.7 5.4 6.2 6.0 5.4 5.9 6.2 6.1 6.0 6.3 6.2 5.8 6.2 6.3 6.3 6.3 6.4 6.5 6.6 6.1 6.3 4.4 6.7
Do the data of Exercise 17.8 (above) give good reason to think that the springtime water the tributary water basin around the Shavers Fork watershed is not neutral. (A neutral pH is the pH of pure water, pH 7.)
Step 1:
STATE: Is there evidence that the springtime water pH of the Shavers Fork watershed is not neutral (pH 7)?
FORMULATE: State hypotheses to be tested.
A. H 0 : μ = 7 vs. Ha : μ > 7
B. H 0 : μ = 7 vs. Ha : μ < 7
C. H 0 : μ = 7 vs. Ha : μ ≠ 7
D. H 0 : μ ≠ 7 vs. Ha : μ < 7
Answers
Answer:
C. H 0 : μ = 7 vs. Ha : μ ≠ 7
Since the calculated value of t = -9.462 falls in the critical region t ≤-2.048
We conclude that the springtime water the tributary water basin around the Shavers Fork watershed is not neutral. We accept our alternate hypothesis and reject the null hypothesis.
Step-by-step explanation:
The null hypothesis the usually the test to be performed. Here we want to check whether the water is neutral or not. Neutral water must have a pH of 7 . This can be stated as the null hypothesis. And the claim is treated as the alternate hypothesis that water in not neutral or not having pH= 7
In symbols it will be written as
H0: : μ = 7 vs. Ha : μ ≠ 7
So choice C is the best option for this hypothesis testing.
Let the significance level be 0.05
The degrees of freedom = n-1= 29-1 = 28
The critical value is t ≥ 2.048 and t ≤ - 2.048 for 0.05 two tailed test with 28 df.
The test statistic to use is t- test
t= x- u/ s/√n
The total sum is 170.9 and mean = x= 5.893
The u = 7
And the sample standard deviation is =s= 0.63
Putting the values
t= 5.893-7/0.63/√29
t= - 1.107/0.11699
t= -9.4623
Since the calculated value of t = -9.462 falls in the critical region t ≤-2.048
We conclude that the springtime water the tributary water basin around the Shavers Fork watershed is not neutral. We accept our alternate hypothesis and reject the null hypothesis.
A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides. Given that there are 30 meters of fencing available, determine the dimensions that would create the garden of maximum area. What is the maximum possible area?
Answers
The dimensions of the garden that create the maximum area are 5 meters by 15 meters, and the maximum possible area is 75 square meters
What is measurement?
Measurement is the process of assigning numerical values to physical quantities, such as length, mass, time, temperature, and volume, in order to describe and quantify the properties of objects and phenomena.
Let's assume that the rock wall is the width of the garden and the wire fencing is used for the length and the other two sides. Let's denote the length of the garden as L and the width as W.
Since we have 30 meters of fencing available, the total length of wire fencing used is:
L + 2W = 30 - W
Simplifying this equation, we get:
L = 30 - 3W
The area of the garden is:
A = LW
Substituting the expression for L from the previous equation, we get:
A = W(30 - 3W)
Expanding the expression, we get:
A = 30W - 3W²
To find the maximum area, we need to take the derivative of A with respect to W and set it equal to zero:
dA/dW = 30 - 6W = 0
Solving for W, we get:
W = 5
Substituting this value back into the expression for L, we get:
L = 15
Therefore, the dimensions of the garden that create the maximum area are 5 meters by 15 meters, and the maximum possible area is:
A = 5(15) = 75 square meters
To know more about measurement visit:
brainly.com/question/4804936
#SPJ1
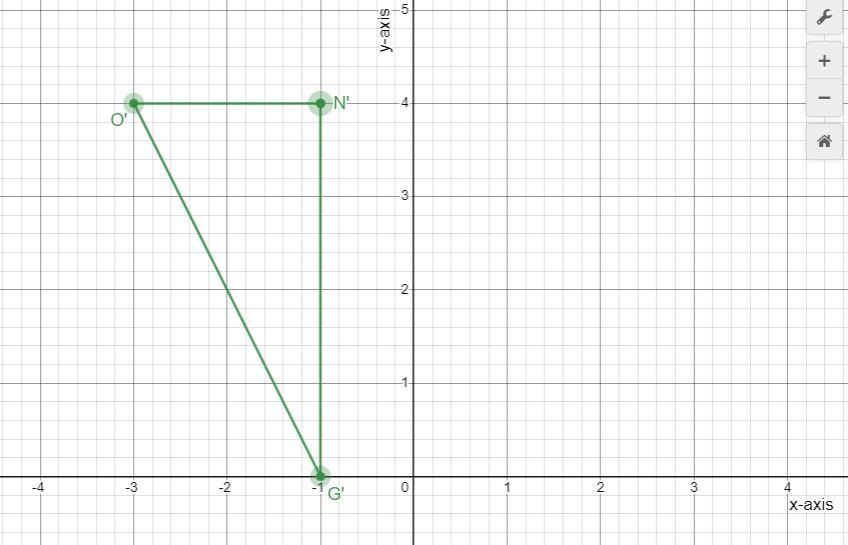
Rotation 90° clockwise about the origin
N
O
G

Answers
An image of triangle NOG after a rotation 90° clockwise about the origin is shown below.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation which moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
Next, we would apply a rotation of 90° clockwise about the origin to the coordinate of this triangle NOG in order to determine the coordinate of its image;
(x, y) → (y, -x)
Point N = (-4, -1) → Point N' (-1, 4)
Point O = (-4, -3) → Point O' (-3, 4)
Point G = (0, -1) → Point G' (-1, 0)
Read more on rotation here: brainly.com/question/28854313
#SPJ1
Which expression is equivalent to the given expression? Assume the denominator does not equal zero.

Answers
Answer:
B
Step-by-step explanation:
\(\dfrac{a^{m}}{a^{n}}=a^{m-n} \ if \ m > n\\\\\\ \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} \ if \ n > m\\\)
\(\dfrac{16r^{6}z^{3}}{8r^{2}z^{6}}=\dfrac{2r^{6-2}}{z^{6-3}}\\\\ =\dfrac{2r^{4}}{z^{3}}\)
(6-2x) +(15-3x) where x=0.2
Answers
\( \sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}\)
Expression: \(\displaystyle\sf (6-2x) +(15-3x)\)
Substituting \(\displaystyle\sf x=0.2\):
\(\displaystyle\sf (6-2(0.2)) +(15-3(0.2))\)
Simplifying the expression inside the parentheses:
\(\displaystyle\sf (6-0.4) +(15-0.6)\)
\(\displaystyle\sf 5.6 +14.4\)
Calculating the sum:
\(\displaystyle\sf 20\)
Therefore, \(\displaystyle\sf (6-2x) +(15-3x)\) evaluated at \(\displaystyle\sf x=0.2\) is equal to \(\displaystyle\sf 20\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
2
Select the correct answer from each drop-down menu.
Triangle ABC is shown in the coordinate plane. It is translated 6 units left and 4 units down. Then it is dilated by a scale factor of 3 centered about the
origin. Complete the statements.
-6 -4
v.
6
4-
2-
lo
-2-
-4-
-6-
The translation of triangle ABC
A
2
с
6
B
Reset
The dilation of triangle ABC
Next
Answers
For the transformations of the triangle, we have that:
1. The translation of triangle ABC preserves side lengths and angles.
2. The dilation of triangle ABC preserves angles but not side lengths.
Hence the correct options are, respectively, C and B.
A translation involves shift left, shift right, shift down, or shift up, meaning that just the coordinates of the figure change, not the angles or the side lengths,
1. The translation of triangle ABC preserves side lengths and angles.
For a dilation, the coordinates of the vertices are multiplied by a constant, hence the side lengths change while the angles remain constant, thus:
2. The dilation of triangle ABC preserves angles but not side lengths.
Hence the correct options are, respectively, C and B.
More can be learned about transformations at brainly.com/question/4521517
#SPJ1

please help me with this sum

Answers
Step-by-step explanation:
2667
1884
1953
782
2046
3105
8559
5368
963
3367
Answer:
381 x 7 = 2667
471 x 4 = 1884
651 x 3 = 1971
391 x 3 = 1173
341 x 6 = 2046
Hope its help full
I will give brainiest to whoever answers correctly !!
Please do not steal my points I'm tired of it put a legit answer or leave!! I will give brainiest to whoever answers correctly!!

Answers
Answer:
15450
Step-by-step explanation:
On the Navajo Reservation, a random sample of 210 permanent dwellings in the Fort Defiance region showed that 70 were traditional Navajo hogans. In the Indian Wells region, a random sample of 141 permanent dwellings showed that 20 were traditional hogans. Let p1 be the population proportion of all traditional hogans in the Fort Defiance region, and let p2 be the population proportion of all traditional hogans in the Indian Wells region.
(a) Find a 95% confidence interval for p1 – p2. (Use 3 decimal places.)
Answers
Using the Confidence-interval formula, we get that the confidence interval for p1-p2 = 1.962.
Define Confidence-interval formula.The term "confidence interval" is used to define the degree of uncertainty surrounding a sampling technique. The probability that the parameter's true value will fall inside a given range is provided by a confidence interval.
A confidence interval estimate of a population mean is often presented as follows: = Sample mean × Standard error of Mean
Given, n1 = 210 and n2 = 141
Sample proportions that have been given are p1 = 70 and p2 = 20
difference of the estimate, p1 - p2 = 50
Confidence interval for p1-p2:
(p1 - p2)-E ≤ (p1-p2) ≤ (p1-p2) + E
Where E = z × √ (p1q1/n1 + p2q2/n2)
Z is the critical value for confidence level.
Putting the values of n1, n2, p1 and p2 we get:
Critical z value, z = 1.962
Standard Error, \(SE_{p1 - p2}\) = NaN
Therefore, ≈95% Confidence Interval:(NaN, NaN).
To know more about Confidence-interval formula, visit:
https://brainly.com/question/14121106
#SPJ1
What is the third step in sketching the graph of a rational function
Answers
Answer:
use test numbers to find where the function is a positive and where it is negative. sketch the function's graph, plotting additional points as guides as negative. choose test numbers to t the left and right of each of these places, and find the value of the function at each test number.
Use the triangle above to find the trigonometric ratios

Answers
9514 1404 393
Answer:
sin(C) = 24/26 (c)cos(C) = 10/26 (a)tan(C) = 24/10 (d)Step-by-step explanation:
The mnemonic SOH CAH TOA can help you remember the definitions of the trig relations:
Sin = Opposite/Hypotenuse
Cos = Adjacent/Hypotenuse
Tan = Opposite/Adjacent
__
In the given triangle, the side adjacent to angle C is marked 10; the side opposite is marked 24; and the hypotenuse is marked 26.
1. sin(C) = 24/26
2. cos(C) = 10/26
3. tan(C) = 24/10
Use the Product Rule of Logarithms to write the completely expanded expression equivalent to log4 (6(5 + 2x)). Make sure
to use parenthesis around your logarithm functions log(x + y).
Answers
\(log_{4}(2) + log_{4}(3)+ log_{4}(5+2x)\) is the completely expanded logarithmic expression .
What are logarithms ?Logarithm, an exponent or power that must be raised to obtain a particular number. Mathematically, if bx = n then x = logb n then x is the logarithm of n to base b. Example: 23 = 8; so 3 is the base 2 logarithm of 8, or 3 = log2 8.
The most common types of logarithms are the base 10 common logarithm, the base 2 binary logarithm, and the base e ≈ 2.71828 natural logarithm.
Calculationsthe product rule for logarithms is
\(log_{b}(MN) = log_{b}(M) + log_{b}(N)\) for b > 0
now ,
\(log_{4}(6(5 + 2x)) \\\\log_{4}(6) + log_{4}(5 + 2x)\\ \\ log_{4}(2.3) + log_{4}(5 + 2x) \\\\ log_{4}(2) + log_{4}(3)+ log_{4}(5 +2x)\)
learn more about logarithms here :
brainly.com/question/28346542
#SPJ13
find the perimeter of the polygon with the given vertices. G(-4,-1) H(1,4) J(4,1) K(-1,-4)
Answers
9514 1404 393
Answer:
16√2 ≈ 22.63
Step-by-step explanation:
A graph is informative. It shows us the sides of the polygon have slopes of ±1, so the perimeter can be figured in units of the diagonal of a unit square. (The length of that diagonal is √2.) The short sides are 3 such units long, and the long sides are 5 such units. Then the total perimeter is ...
P = 2(3 +5)√2
P = 16√2 ≈ 22.63

Write the line equation passing through (-4,-1) and parallel to y=-1/2x+1
Answers
Answer:
\(y=-\dfrac{1}{2}x-3\)
Step-by-step explanation:
\(\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}\)
Given equation:
\(y=-\dfrac{1}{2}x+1\)
Parallel lines have the same slope.
Therefore, the slope of the line parallel to the given equation is:
\(m=-\dfrac{1}{2}\)
Substitute the found slope and given point (-4, -1) into the point-slope formula:
\(\implies y-(-1)=-\dfrac{1}{2}(x-(-4))\)
\(\implies y+1=-\dfrac{1}{2}(x+4)\)
\(\implies y+1=-\dfrac{1}{2}x-2\)
\(\implies y=-\dfrac{1}{2}x-3\)
Therefore, the equation of the line passing through (-4, -1) and parallel to the given equation is:
\(\boxed{y=-\dfrac{1}{2}x-3}\)