Answers
Related Questions
Factories A and B sent rice to stores 1 and 2. A sent 14 loads and B sent 22. Store 1 used 20 loads and
store 2 used 16. It cost $200 to ship from A to 1, $350 from A to 2, $300 from B to 1, and $250 from B
to 2. $8600 was spent. How many loads went where ?
Answers
Factory A sent 14 loads of rice to Store 1
Factory A sent no loads of rice to Store 2
Factory B sent 6 loads of rice to Store 1
Factory B sent 16 loads of rice to Store 2
Let
A1 = Loads sent from Factory A to Store 1
A2 = Loads sent from Factory A to Store 2
B1 = Loads sent from Factory B to Store 1
B2 = Loads sent from Factory B to Store 2
Then, the equations describing the scenario are;
\(A1+A2=14\)
\(B1+B2=22\)
\(A1+B1=20\)
\(A2+B2=16\)
\(200A1+350A2+300B1+250B2=8600\)
The simultaneous equations can be expressed in matrix form thus:
\(\left[\begin{array}{ccccc}{A1}&{A2}&{B1}&{B2}&{}\\1&1&0&0&14\\0&0&1&1&22\\1&0&1&0&20\\0&1&0&1&16\\200&350&300&250&8600\end{array}\right]\)
Reducing the matrix:
Step 1:
\(R_3 \leftarrow R_3 - R_1\\R_5 \leftarrow R_5 - 200R_1\)
\(\left[\begin{array}{ccccc}{A1}&{A2}&{B1}&{B2}&{}\\1&1&0&0&14\\0&0&1&1&22\\0&-1&1&0&6\\0&1&0&1&16\\0&150&300&250&5800\end{array}\right]\)
Step 2:
Switch \(R_4\) and \(R_2\)
\(\left[\begin{array}{ccccc}{A1}&{A2}&{B1}&{B2}&{}\\1&1&0&0&14\\0&1&0&1&16\\0&-1&1&0&6\\0&0&1&1&22\\0&150&300&250&5800\end{array}\right]\)
Step 3:
\(R_3\leftarrow R_3+R_2\\R_5 \leftarrow R_5-150R_2\)
\(\left[\begin{array}{ccccc}{A1}&{A2}&{B1}&{B2}&{}\\1&1&0&0&14\\0&1&0&1&16\\0&0&1&1&22\\0&0&1&1&22\\0&0&300&100&3400\end{array}\right]\)
Step 4:
\(R_4\leftarrow R_4+R_3\\R_5 \leftarrow R_5-300R_3\)
\(\left[\begin{array}{ccccc}{A1}&{A2}&{B1}&{B2}&{}\\1&1&0&0&14\\0&1&0&1&16\\0&0&1&1&22\\0&0&0&0&0\\0&0&0&-200&-3200\end{array}\right]\)
Step 5:
Switch \(R_4\) and \(R_5\)
\(R_4\leftarrow R_4 \times \frac{1}{-200}\\R_1 \leftarrow R_1-R_2\)
\(\left[\begin{array}{ccccc}{A1}&{A2}&{B1}&{B2}&{}\\1&0&0&-1&-2\\0&1&0&1&16\\0&0&1&1&22\\0&0&0&1&16\\0&0&0&0&0\end{array}\right]\)
Step 6:
\(R_1 \leftarrow R_1 + R_4\\R_2\leftarrow R_2 - R_4\\R_3 \leftarrow R_3-R_4\)
\(\left[\begin{array}{ccccc}{A1}&{A2}&{B1}&{B2}&{}\\1&0&0&0&14\\0&1&0&0&0\\0&0&1&0&6\\0&0&0&1&16\\0&0&0&0&0\end{array}\right]\)
So,
\(A1=14\\A2=0\\B1=6\\B2=16\)
From the above calculations, we see that
Factory A sent 14 loads of rice to Store 1
Factory A sent no loads of rice to Store 2
Factory B sent 6 loads of rice to Store 1
Factory B sent 16 loads of rice to Store 2
Learn more about Matrix row operations: https://brainly.com/question/18546657
find the volume of the shaded solid below
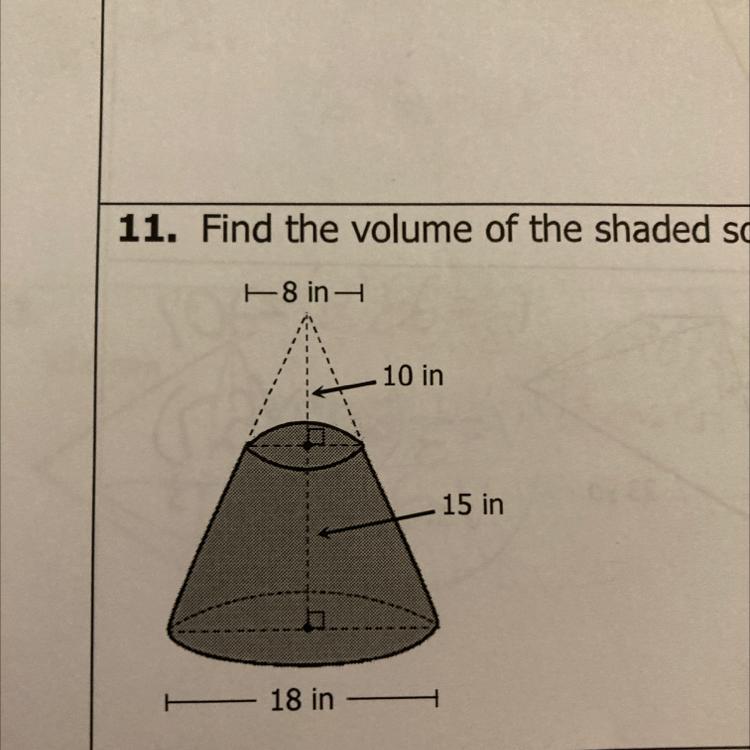
Answers
The volume of the shaded portion of the cone is V = 621.667 inches³
Given data ,
Let the volume of the shaded region be V
Now , the volume of the larger cone be A
Let the volume of the smaller cone be B
Volume of Cone = ( 1/3 ) πr²h
V = A - B
And , A = ( 1/3 ) ( 9 )² ( 25 )
On simplifying , we get
A = ( 1/3 ) ( 81 ) ( 25 )
A = 675 inches³
And , B = ( 1/3 ) ( 4 )² ( 10 )
B = ( 160/3 ) inches³
So , Volume of shaded region V = A - B
V = 675 inches³ - ( 160/3 ) inches³
V = ( 1,865/3 ) inches³
V = 621.667 inches³
Hence , the volume of cone is 621.667 inches³
To learn more about cone click :
https://brainly.com/question/1984638
#SPJ1
find dy/dx and d2y/dx2, and find the slope and concavity (if possible) at the given value of the parameter. (If an answer does not exist, enter DNE.) Parametric Equations Point x = 6 cos θ, y = 6 sin θ θ = π/4
find:
dy/dx=
d^2y/dx^2 =
slope
concavity:
Answers
The value of dy/dx is -cotθ, d^2y/dx^2 is -6cosec³θ, slope is -cotθ, concavity is -6cosec³θ.
Parametric Equations Point x = 6cosθ, y = 6sinθ and θ = π/4
We have to determine the value of dy/dx.
We can define dy/dx as;
dy/dx = (dy/dθ)/(dx/dθ)
We first define dy/dθ and dx/dθ.
x = 6cosθ y = 6sinθ
dx/dθ = -6sinθ dy/dθ = 6cosθ
Now put the value
dy/dx = 6cosθ/(-6sinθ)
dy/dx = -cotθ
Now we have to determine the value of d²y/dx².
d²y/dx² = d/dx(dy/dx)
We can write it as
d²y/dx² = \(\frac{\frac{d}{d\theta}(\frac{dy}{dx})}{dx/d\theta}\)
We first determine the value of d/dθ(dy/dx)
d/dθ(dy/dx) = d/dθ(-cotθ)
d/dθ(dy/dx) = cosec²θ
Now put the value
d²y/dx² = cosec²θ/(-6sinθ)
d²y/dx² = -6cosec³θ
Now we have to determine the slope.
Slope = dy/dx
Slope = -cotθ
Now we have to determine the concavity.
Concavity = d²y/dx²
Concavity = -6cosec³θ
To learn more about concavity link is here
brainly.com/question/13320130
#SPJ4
When sample size increases:____.
A. Standard deviation of the sample mean increases.
B. Confidence interval remains the same.
C. Confidence interval increases.
D. Confidence interval decreases.
Answers
Answer:
D. Confidence interval decreases.
Step-by-step explanation:
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
When sample size increases:
The standard deviation of the sample mean is:
\(s = \frac{\sigma}{\sqrt{n}}\)
That is, it is inversely proportional to the sample size, so if the sample size incerases, the standard deviation decreases, and so does the confidence interval.
This means that the correct answer is given by option D.
Pie chart values
20%. Rice
15%. Others
Pulses. 30%
maize 20%
wheat 15%
Percentage distribution of products in exports of the
given countries.
(a) What is the value (in $ billion) of pulses export
by US? on a billion
(6)
What is the ratio of wheat export of UK to
maize export of IND? 4:10
(e) By what percentage is the maize export of
JAP more than the rice export of AUS?
(d) If the export of AUS is doubled and that of US is
halved but percentage distribution of products of
export remains the same, then find the value of
Export of Rice by US
Export of Pulses by AUS
In USSR, find the ratio of maize export to the
rice export.

Answers
a.) The value of pulses exported by US in billion would be=30 billion.
b.) The ratio of wheat export of UK to maize export of IND would be= 6:5
How to calculate the value of pulses exported?For question a.)
To calculate the pulses, the following steps should be taken as follows:
From the bar chart, the value of pulses in billions = 30 billions.
For question b.)
The ratio of wheat export at UK and maize export at IND would be calculated as follows:
The quantity of wheat export at UK = 24
The quantity of maize export at IND = 20
Therefore, the ratio of wheat to maize = 24:20= 6:5
Learn more about ratio here:
https://brainly.com/question/2328454
#SPJ1
what are the domain and range of this exponectial function y=1\9.4x
Answers
Answer:
Fourth choice: - Domain: All real numbers ; Range {y | y > 0}
Explanation:
The domain of the function is the set of x values for which y is defined.
The range of the function is the set of y value that y can take.
Now for our function
\(y=\frac{1}{9}\cdot4^x\)x can take any real value; it is defined for both positive
Find the savings plan balance after 9 months with an APR of 8% and monthly payments of $250.
Answers
Answer:
$159.24 is the balance after 9 months is the answer that you seek
Step-by-step explanation:
Answer:
the savings plan balance after 9 months with an APR of 8% and monthly payments of $250 is approximately $2,366.98.
Step-by-step explanation:
To find the savings plan balance after 9 months with an APR of 8% and monthly payments of $250, we can use the formula for the future value of an annuity:
FV = Pmt x ((1 + r/n)^(n x t) - 1) / (r/n)
where:
FV = future value
Pmt = monthly payment
r = annual interest rate
n = number of compounding periods per year
t = time in years
In this case, we have:
Pmt = $250
r = 8%
n = 12 (since payments are made monthly)
t = 9/12 = 0.75 (since 9 months is three-quarters of a year)
Substituting these values into the formula, we get:
FV = $250 x ((1 + 0.08/12)^(12 x 0.75) - 1) / (0.08/12)
FV ≈ $2,366.98
Therefore, the savings plan balance after 9 months with an APR of 8% and monthly payments of $250 is approximately $2,366.98.
What is the focus of the parabola? y=−1/4x^2 −2x − 2
Answers
Answer:
Step-by-step explanation:
This is a doozy. You have to know A LOT about parabolas to get to this answer. First and foremost, we will have to complete the square on the x terms and get everything else on the other side of the equals sign with the intention of putting this into standard form which looks like this:
\(-4p(y-k)=(x-h)^2\)
The negative is because the parabola is upside down. We begin breaking it down by multiplying everything by -4 to get:
\(-4y=x^2+8x+8\) and subtract that 8 from both sides to get:
\(-4y-8=x^2+8x\). Now we'll complete the square on the x terms by taking half the linear term, squaring it, and then adding it to both sides. Our linear term (the number with the x stuck to it) is 8. Half of 8 is 4 ad 4 squared is 16. So we add 16 to both sides to get:
\(-4y-8+16=(x^2+8x+16)\)
The right side will simplify into a perfect square binomial and the left side we will just combine like terms to get:
\(-4y+8=(x+4)^2\)
We're getting close. Now we need to just factor out the -4 on the left to get:
\(-4(y-2)=(x+4)^2\)
If the standard form is -4p blah blah blah, then p has to be 1. That means that the focus is 1 unit below the vertex. The vertex is (-4, 2). p is the distance between the vertex and the focus. The focus is always on the axis of symmetry. We know that the parabola opens upside down because of the negative sign, and the parabola always wraps itself around the focus. That's why the focus is p units below the vertex. That means that the focus is located at (-4, 1).
Told you it was difficult. I noticed no one helped you with this one and it's been up here for 5 days...
Arely is making a necklace of beads. For every 3 silver
beads, there is 1 crystal bead and 2 purple beads. If
there are 36 beads in the necklace, how many silver,
crystal, and purple beads are there?
Answers
Divide 36 by 6 to get 6.
Now multiply the numbers in the ratio by 6 and you should get....
18 : 6 : 12
Notice how if you add those up you get 36
So: there are 18 silver beads, 6 crystal and 12 purple
Hope this helps! Any questions let me know :)
The average length of a baby at birth is 19 inches long. There are 2.54 centimeters in 1 inch. What is the average length of a baby at birth in centimeters.
Answers
Answer:
16.46 I don't know
Step-by-step explanation:
Name a pair of lines that are parallel
Answers
you didn't include the picture, so I cant see what the question is, sorry.
or if you mean any lines they just have to not intersect or combined at any point like the image I attached, that is parallel lines when they never touch.

Which shape has at least one one pair of perpendicular sides?

Answers
Answer:
the square
Step-by-step explanation:
perpendicular = 90 degrees
Square (Option 1) has at least one pair of perpendicular sides
What is perpendicular?"Perpendicular means two lines, or sides, that meet at a right angle. A right angle is the measurement of 90 degrees."
What are perpendicular sides?"Perpendicular sides are at a 90-degree angle. Since they are so common, there is a special symbol to signify the sides are perpendicular without measuring."
Option 1
Squares are made up of two sets of parallel line segments, and their four 90° angles mean that those segments also happen to be perpendicular to one another.
Option 2
A parallelogram is a special kind of quadrilateral that is formed by parallel lines. The angle between the adjacent sides of a parallelogram may vary but the opposite sides need to be parallel for it to be a parallelogram.
Option 3
There are three angles in a triangle. These angles are formed by two sides of the triangle, which meets at a common point, known as the vertex. The sum of all three interior angles is equal to 180 degrees.
Option 4
A trapezoid is a quadrilateral with exactly one pair of parallel sides. Isosceles trapezoids have two sides which are equal sized and have the same angles between themselves and the bases.
Hence, Square (Option 1) has at least one pair of perpendicular sides
Learn more about shapes here
https://brainly.com/question/23082802
#SPJ2
Assume the readings on thermometers are normally distributed with a mean of 0degreesC and a standard deviation of 1.00degreesC. Find the probability that a randomly selected thermometer reads between negative 2.05 and negative 1.49 and draw a sketch of the region.
Answers
Answer:
\(P(-2.05<X<-1.49)=P(\frac{-2.05-\mu}{\sigma}<\frac{X-\mu}{\sigma}<\frac{-1.49-\mu}{\sigma})=P(\frac{-2.05-0}{1}<Z<\frac{-1.49-0}{1})=P(-2.05<z<-1.49)\)
And we can find this probability with this difference
\(P(-2.05<z<-1.49)=P(z<-1.49)-P(z<-2.05)=0.068- 0.0202= 0.0478\)
And we can see the figure in the plot attached.
Step-by-step explanation:
Let X the random variable that represent the redings on thermometers of a population, and for this case we know the distribution for X is given by:
\(X \sim N(0,1)\)
Where \(\mu=0\) and \(\sigma=1\)
We are interested on this probability
\(P(-2.05<X<-1.49)\)
We can use the z score formula given by:
\(z=\frac{x-\mu}{\sigma}\)
Using this formula we got:
\(P(-2.05<X<-1.49)=P(\frac{-2.05-\mu}{\sigma}<\frac{X-\mu}{\sigma}<\frac{-1.49-\mu}{\sigma})=P(\frac{-2.05-0}{1}<Z<\frac{-1.49-0}{1})=P(-2.05<z<-1.49)\)
And we can find this probability with this difference
\(P(-2.05<z<-1.49)=P(z<-1.49)-P(z<-2.05)=0.068- 0.0202= 0.0478\)
And we can see the figure in the plot attached.

Answer below
Brainliest

Answers
Answer:
25 remainder of 4
Step-by-step explanation:
Answer:
here hope this will be you ^^"
▃▃▃▃▃▃▃▃▃▃▃▃▃▃▃▃▃▃▃▃▃

solve the following inequality for n -5n+6≥-7(5n-6)-6n
Answers
Answer: The inequality is: n ≥ 36/37
Step-by-step explanation:
Let's solve your inequality step-by-step.
n − 5n + 6 ≥ −7(5n−6)−6
----------------------------------------------------------------------------------------------------------------
Step 1: Simplify both sides of the inequality.
−4n + 6 ≥ −41n + 42
----------------------------------------------------------------------------------------------------------------
Step 2: Add 41n to both sides.
−4n + 6 + 41n ≥ − 41n+ 42 + 41n
37n + 6 ≥ 42
----------------------------------------------------------------------------------------------------------------
Step 3: Subtract 6 from both sides.
37n + 6 − 6 ≥ 42 − 6
37n ≥ 36
----------------------------------------------------------------------------------------------------------------
Step 4: Divide both sides by 37.
37n/37 ≥ 36/37
n ≥ 36/37
----------------------------------------------------------------------------------------------------------------
Answer:
n ≥ 36/37
Source: https://www.mathpapa.com/calc.html?q=x+y%3D7%2C%20x+2y%3D11
, Hope this helps :)
Have a great day!!
how to solve this question?

Answers
The revised Doubtful Debts Provision should be, $4,555.
Now, Using a net debtors value of $91,100 and a provision rate of 5%, use the calculation to get the adjusted Provision for Doubtful Debts (PDD):
Net Debts x Provision Rate equals Adjusted PDD.
The computation would then be:
= $91,100 x 0.05
= $4,555 is the adjusted PDD.
Because of the additional $550 in bad debt and the revised net debtors value of $91,100, the Provision for Doubtful Debts must be raised by ,
= $4,555 - $3,500
= $1,055
Hence, The revised Doubtful Debts Provision should be $4,555.
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
I need help asapp Imaoo


Answers
Answer:
correct
Step-by-step explanation:
find the missing angle measure in each triangle. Then classify the triangle as acute, right, or obtuse. PLEASE ANSWER QUICK ILL MARK BRAINLIEST

Answers
Answer:
40 Right Angle Triangle
Step-by-step explanation:
180-50-90=x
x=40
Right angle triangle
Answer:
40
Step-by-step explanation:
90 + 50 = 140
A triange = 180
A right angle(aka the square) = 90
180 - 140 = 40
x = 40
Mauna Loa is one of the most active volcanoes in the world. From 1832 to 1950, the Hawaiian landmark erupted 37 times. What probability distribution will be used to estimate the chance that the next two Mauna Loa eruptions will occur within five months of one another
Answers
Answer:
\(E \approx \exp(0.31)\)
Step-by-step explanation:
From the question we are told that
Occurrence of volcanoes\(x=37 times\)
The number year
\(N= 1832-1950\\N=118 years\)
Generally the number of volcanoes occurring is mathematically modeled as
\(X \approx Poisson(0.31)\)
Generally the waiting time of the earthquakes will also be modeled with exponential distribution with the same parameters
\(E \approx \exp(0.31)\)
Please help. Use the alternative form of definition of derivative to find the slope of the line tangent. Please show work. 100 points. Will give brainliest, when it comes up.

Answers
The slope of the line tangent to the graph of h(x) = 1/x + 3 at the point when x is -6 is -1/36.
What is the slope of the line tangent to the equation?To determine the slope of the line tangent to the graph of the given function when x = -6;
Using alternative form of the definition of derivative.
f'(a) = lim (h->0) [f(a+h) - f(a)] / h
Using this formula for the given function;
h'(a) = lim (h->0) [h(a+h) - h(a)] / h
Now, substitute a = -6 into the formula:
h'(-6) = lim (h->0) [h(-6+h) - h(-6)] / h
Next, simplify the expression by plugging in the values:
h'(-6) = lim (h->0) [1/(-6+h) + 3 - (1/-6 + 3)] / h
Simplifying further:
h'(-6) = lim (h->0) [1/(-6+h) - 1/-6] / h
Now, let's combine the fractions with a common denominator:
h'(-6) = lim (h->0) [(-6 - (-6+h))/((-6+h)(-6))] / h
Simplifying the numerator:
h'(-6) = lim (h->0) [-h / ((-6+h)(-6))] / h
Canceling out the h's:
h'(-6) = lim (h->0) [-1 / ((-6+h)(-6))]
Taking the limit as h approaches 0:
h'(-6) = -1 / ((-6)(-6))
Simplifying further:
h'(-6) = -1 / 36
Learn more on slope of line tangent here;
https://brainly.com/question/6353432
#SPJ1
Fill in the blanks using the following choices: reject, fail to reject, sufficient, enough, not sufficient, not enough If the p value is 0.32 to test if there is a difference exists between the proportion of students who have ear infections at one school and the other, your decision is to the null and the conclusion: There is evidence to support the alternative that the proportion of students who have ear infections at one school and the other are different.
Answers
Answer:
FAIL TO REJECT
NOT ENOUGH
Step-by-step explanation:
Given a Pvalue of 0.32
Decision region :
When Pvalue < α ; Reject the Null and conclude that there is significant or enough evidence to accept the alternative hypothesis.
Otherwise, fail to reject reject the null and conclude that, there is not enough evidence to accept the alternative hypothesis
Therefore, for the scenario above, where Pvalue = 0.32
Possible α values are ; 0.1, 0.05, 0.01
For all α - values listed, the Pvalue is greater than α
Pvalue > α ; Hence, FAIL TO REJECT the Null.
Conclusion :
There is NOT ENOUGH evidence to support the alternative that the proportion of students who have ear infection at one school and the other is different.
Let x= −1. Evaluate the function for y. y=7.2x+3
Answers
Answer:
y = -4.2
hope it's helpful ❤❤❤❤❤❤
THANK YOU.

15 Calculate the appropriate measure of Skewness for the data below 0-10 10-20 20-30 | 30-40 40-50 50-60 25 No of workers 10 35 40 50
Answers
Answer:6. Calculate the appropriate measure of Skewness for the data below. Class 0-10 10-20 20-30 30-40 40-50 50-60 12 25 35 40 50 No. of workers 10 Ans: -0.49
Step-by-step explanation:
True or False: In order to prove that two functions are inverses, you can show that f (g(x)) = x AND show that g (f ()) = x. This is using
composition to prove inverses.
Answers
Answer:
true
Step-by-step explanation:
trust me
siete veces un número en expresión algebraica
Answers
In algebra, "seven times a number" is written as 7x, which is the multiplication of seven instances of the symbol x.
What is the formula for algebraic expressions?An equation that includes constants, variables, and a few algebraic operations is said to be algebraic. A good example of an algebraic expression is 3x2 2xy + d. So, three different types of fundamental building blocks make up an algebraic expression: Coefficient (i.e. numbers) (i.e. numbers)
A seven-times-a-number is represented by multiplying it by seven or adding it to another integer (since this is an abbreviated successive addition ).
If x is any number, then it may be written as follows seven times: Algebraic expressions (numbers or letters) are linked by fundamental operations including addition, subtraction, multiplication, and division in mathematical language.
To learn more about algebraic expression from given link
https://brainly.com/question/4541471
#SPJ1
Complete question -
Seven times a number in algebraic expression
I think it’s 40%, am I correct?

Answers
my thought process is
There are 100 ticks (20 spaces with 5 marks)
the area it wants has 6 large spaces (6*5=30) and 3 marks
30+3 is 33
Solve for x. Round to the nearest tenth, if necessary

Answers
Answer:
Set your calculator to degree mode.
cos(37°) = 52/x
x cos(37°) = 52
x = 52/cos(37°) = 65.1
Julian is using a biking app that compares his position to a simulated biker traveling Julian's target speed. When Julian is behind the simulated biker, he has a negative position.
Julian sets the simulated biker to a speed of
20
km
h
20
h
km
20, start fraction, start text, k, m, end text, divided by, start text, h, end text, end fraction. After he rides his bike for
15
1515 minutes, Julian's app reports a position of
−
2
1
4
km
−2
4
1
km minus, 2, start fraction, 1, divided by, 4, end fraction, start text, k, m, end text.
What has Julian's average speed been so far?
Answers
To solve the problem, we need to find Julian's average speed, given that he started biking from a position behind the simulated biker at a speed of 20 km/h, and after 15 minutes, his position was reported as -214 km.
We can use the formula for average speed:
Average speed = total distance / total time
To find the total distance, we need to calculate the displacement of Julian from the initial position of -d (where d is the distance between Julian and the simulated biker when he started biking) to the position of -214 km after 15 minutes.
Displacement = final position - initial position
Displacement = (-214 km) - (-d) = d - 214 km
The total distance covered by Julian is equal to the absolute value of the displacement, since the direction of the motion does not matter when computing distance.
Total distance = |d - 214 km|
To find the total time, we need to convert 15 minutes to hours:
Total time = 15 minutes / 60 minutes/hour = 0.25 hours
Now we can substitute the values into the formula for average speed:
Average speed = total distance / total time
Average speed = |d - 214 km| / 0.25 hours
Since Julian was traveling at a constant speed of 20 km/h, we can also express the distance in terms of time:
Average speed = (20 km/h) x t / 0.25 hours
where t is the time Julian biked in hours.
Setting the two expressions for average speed equal to each other, we can solve for t:
|d - 214 km| / 0.25 hours = (20 km/h) x t / 0.25 hours
|d - 214 km| = 20 km/h x t
Solving for t:
t = |d - 214 km| / 20 km/h
Now we can substitute this expression for t into either expression for average speed:
Average speed = (20 km/h) x t / 0.25 hours
Average speed = |d - 214 km| / 0.25 hours
Substituting the expression for t:
Average speed = |d - 214 km| x 4 / |d - 214 km|
Simplifying:
Average speed = 80 km/h
Therefore, Julian's average speed so far has been 80 km/h.
Child Health and Development Studies (CHDS) has been collecting data about expectant mothers in Oakland, CA since 1959. One of the measurements taken by CHDS is the weight increase (in pounds) for expectant mothers in the second trimester. In a fictitious study, suppose that CHDS finds the average weight increase in the second trimester is 14 pounds. Suppose also that, in 2015, a random sample of 45 expectant mothers have mean weight increase of 16.3 pounds in the second trimester, with a standard deviation of 5.9 pounds. A hypothesis test is done to see if there is evidence that weight increase in the second trimester is greater than 14 pounds. Find the p -value for the hypothesis test. The p -value should be rounded to 4 decimal places.
Answers
Answer:
0.9955
Step-by-step explanation:
Given :
Mean weight increase , μ = 14
Sample mean weight increase , xbar = 16.3
Standard deviation, s = 5.9
Sample size, n = 45
Hypothesis :
H0 : μ = 14
H1 : μ > 14
The test statistic : (xbar - μ) ÷ (s/sqrt(n))
Test statistic = (16.3 - 14) ÷ (5.9/sqrt(45))
Test statistic = 2.3 / 0.8795200
Test statistic = 2.615
The Pvalue :
P(Z < 2.615) = 0.99554
Hence, pvalue = 0.9955 (4 decimal places).
Evaluate Cross multiply :)

Answers
5x = 30
5x/5 = 30/5
x=6
