Please help this pea sized brain
8 x (-2) : 4 x 0 =
Answers
Answer:
undefined
Step-by-step explanation:
8 x (-2) : 4 x 0
undefined because denominator is zero
Related Questions
Translate the following into math expression: " 3 more than a number is 5 less than double this number ."
Answers
Answer:
3 + n = 2n - 5
Step-by-step explanation:
let 'n' equal 'a number'
'more than' implies 'addition', so 3 + n
'is' in math implies 'equals', so 3 + n =
'double the number' means to multiply it by 2
'less than' implies 'subtraction'
So final result is:
3 + n = 2n - 5
suppose that 1% of (binary) bits received by your smartphone have errors. what is the probability that the 27th bit received by your smartphone is the first erroneous bit?
Answers
The probability that any given bit received by the smartphone is erroneous is 1%, or equivalently, the probability that any given bit is correct is 99%.
The probability that the 27th bit is the first erroneous bit means that the previous 26 bits were all correct. The probability of this happening is:
P(all previous 26 bits are correct) = (0.99)^26
Now, given that the previous 26 bits were all correct, the probability that the 27th bit is erroneous is simply 1% or 0.01.
Therefore, the overall probability that the 27th bit received by the smartphone is the first erroneous bit is:
P(27th bit is first erroneous bit) = P(all previous 26 bits are correct) x P(27th bit is erroneous | all previous 26 bits are correct)
= (0.99)^26 x 0.01
= 0.0081 or approximately 0.81%
Fill in the table using this function rule

Answers
2 = 16 (24-4(2)=16)
5 = 4 (24-4(5)=4)
6 = 0 (24-4(6)=0)
⚠️⚠️ Easy points if you are good at math ⚠️⚠️
(It kept turning the photo a weird way after I take the photo so I apologize for that)

Answers
Answer:
its C!
Step-by-step explanation:
i think
Answer:
your answer is A, y = -x -1
Step-by-step explanation:
that should be right :)
Find the cube roots of unity in standard form (a+bi). Use exact values.
Answers
Every non-zero complex number has three cube roots. In general, any non-integer exponent, like
1
3
here, gives rise to multiple values. The way we find them is by multiplying
z
by 1 before exponentiating. We write
1
using Euler's Identity to the
2
k
power for integer
k
. That's
Help me I need to pass

Answers
Please refer to the attachment for the answer and explanation! Hope it helps!!:))

Did americans work less than 40 hours a week on average in 1977? in 1977, the gss included questions about the number of hours that the respondent worked per week. The average number of hours worked per week was 34. 61 hours with a standard deviation of 14. 77 hours. A sample of 32 respondents was questioned. Find the test statistic.
Answers
The test statistic is, -2.06.
What is test statistic?
A programme and any related documentation are examined during static testing, a type of software testing that does not call for the programme to be run. Software testing also includes dynamic testing, which involves interacting with the application as it is being used.
Given: Americans work less than 40 hours a week on average in 1977?
In 1977, the GSS included questions about the number of hours that the respondent worked per week.
The average number of hours worked per week was 34. 61 hours with a standard deviation of 14. 77 hours.
A sample of 32 respondents was questioned.
So, the test statistics is,
Z = (x bar - μ)/(σ /√n)
= (34.61 - 40)/(14.77/sqrt(32))
Z = -2.06
Hence, the test statistics is -2.06.
To know more about the test statistic, click on the link
https://brainly.com/question/15980493
#SPJ4
help me solve this question plssss
81m⁴-n⁴
Answers
Step-by-step explanation:
=81m⁴-n⁴
={(3m)²}²-(n²)²
=(3m²+n²)(3m²-n²)
hope it helps.
Can a cylinder produce a cross section that has 4 straight sides?
Answers
Answer:
no
Step-by-step explanation:
No, a cylinder cannot produce a cross section that has 4 straight sides. A cylinder is a three-dimensional object that has a circular base and a curved surface that extends from the base to the top. Any cross section of a cylinder taken parallel to its base will produce a shape that is congruent to the base, which is a circle. Therefore, any cross section of a cylinder will be a circle or an ellipse, which do not have straight sides.
On the other hand, a prism is a three-dimensional object that has two congruent parallel bases and flat, rectangular or parallelogram-shaped sides that connect the bases. A prism can produce a cross section that has 4 straight sides, which would be a rectangle or a parallelogram.
Rufus collected 125 pounds of aluminium cans to recycle. He plans to collect an additional 50 pounds each week.
1. Write an equation for the total pounds, P, of aluminium cans after w weeks.
2. Graph this relationship (Please graph this realtionship on the picture below)
3. What does the slope and y-intercept represent?

Answers
1) The equation is y = 50x + 125
2) On the image at the end.
3) The y-intercept is the initial amount and the slope is the amount he adds per week.
How to write the equation?We know that he starts with 125 pounds, and then he adds 50 pounds per week, so after x weeks, he will have a total of:
y = 50x + 125
This is a linear equation with a slope of 50 and an y-intercept of 125.
The slope tells us how much he adds per week, the y-intercept tells us the initial amount.
To graph this line find two points on the line, you can do that by evaluating:
if x = 0
y = 50*0 + 125 = 125 ---> we have (0, 125)
if x = 1
y = 50*1 + 125 = 175 ---> we have (1, 175)
Now graph these two points and connect them with a line.
Learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1

Can somebody help me please!!!
Answers
Answer:
sure what do you need help on
Step-by-step explanation:
Answer:
whats the question?
the radius of the earth - the distance from surface to core - is 6,370 kilometers. the planet neptune is 24,620 kilometers. if a scale model of the earth is drawn with a radius of 2.5 centimeters, how large would a scale model of neptune have to be drawn? group of answer choices 9848 cm 9.7 cm 2548 cm 0.02548 cm 3.86 cm
Answers
We may build up a proportion and solve for the scale model radius of Neptune using the ratio between the radii of the two planets and the known scale model radius of the Earth. The scale model of Neptune that is produced has a radius of around 9.7 cm.
We may take advantage of the fact that the ratio between the two planets' radii and the ratio between their respective scale model radii is the same. Let's name the Neptune scale model radius "r" Then, we may set up the ratio shown below:
Neptune's radius is equal to the product of Earth's radius and its scale model.
With the provided values, we may simplify and obtain:
24620 km / 6370 km equals 2.5 cm / r
We obtain the following when solving for "r":
r = (24620 km * 2.5 cm) / (6370 km)
r ≈ 9.7 cm
Therefore, a scale model of Neptune would have to be drawn with a radius of approximately 9.7 cm.
Learn more about scale models here:
https://brainly.com/question/17581605
#SPJ4
Brick San Antonio playing a game of counter Rick ha ome counter Selma ha twice a many counter a Rick Tony ha ix counter Leton Selma in total they have 54 counter the number of count a Rick ha: the number of count a Tony ha = 1: P work out the value of paid
Answers
The number of counters Rick has is equal to 12 counters.
The number of counters Tony has is equal to 1:1.5.
The value of p is 1.5.
In order to solve this word problem, we would assign variables to the unknown numbers and then translate the word problem into algebraic equation as follows:
Let R represent the number of counters Rick has.
Let S represent the number of counters Selma has.
Let O represent the number of counters Tony has.
Let T represent total number of counters.
Translating the word problem into an algebraic equation, we have;
S = 2R .....equation 1.
O = 2R - 6 ......equation 2.
T = R + S + O ......equation 3.
Substituting equation 1 and equation 2 into equation 3, we have:
T = R + S + O
54 = R + 2R + 2R - 6
54 = 5R - 6
5R = 54 + 6
5R = 60
R = 60/5
R = 12 counters.
For Tony, the number of counters is given by:
O = 2R - 6
O = 2(12) - 6
O = 24 - 6
O = 18 counters.
In ratio form, we have:
O = 1:P
O = 1:(18/12)
O = 1:1.5
The number of counters Rick has is equal to 12 counters.
The number of counters Tony has is equal to 1:1.5.
The value of p is 1.5.
learn more about word problem,
https://brainly.com/question/29027588
#SPJ4
Letf(x, y) = 2ex − y.Find the equation for the tangent plane to the graph of f at the point
Answers
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b. This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
To find the equation for the tangent plane to the graph of the function f(x, y) = 2e^x - y at a given point (x0, y0), we need to calculate the partial derivatives of f with respect to x and y at that point.
The partial derivative of f with respect to x, denoted as ∂f/∂x or fₓ, represents the rate of change of f with respect to x while keeping y constant. Similarly, the partial derivative of f with respect to y, denoted as ∂f/∂y or fᵧ, represents the rate of change of f with respect to y while keeping x constant.
Let's calculate these partial derivatives:
fₓ = d/dx(2e^x - y) = 2e^x
fᵧ = d/dy(2e^x - y) = -1
Now, we have the partial derivatives evaluated at the point (x0, y0). Let's assume our point of interest is (a, b), where a = x0 and b = y0.
At the point (a, b), the equation for the tangent plane is given by:
z - f(a, b) = fₓ(a, b)(x - a) + fᵧ(a, b)(y - b)
Substituting fₓ(a, b) = 2e^a and fᵧ(a, b) = -1, we have:
z - f(a, b) = 2e^a(x - a) - (y - b)
Now, let's substitute f(a, b) = 2e^a - b:
z - (2e^a - b) = 2e^a(x - a) - (y - b)
Rearranging and simplifying:
z = 2e^a(x - a) - (y - b) + 2e^a - b
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b.
This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
Learn more about tangent here:
https://brainly.com/question/10053881
#SPJ11
On Gabriela’s first birthday, her parents gave her a $50 savings account. On every birthday after that her parents added to the account, increasing the amount they deposited by $25 each year. Complete the recursive definition for the sequence that represents this situation by finding the values for a1 and d.
Answers
We will see that the first term is $50, and the common difference is $25, then the recursive formula is:
aₙ = aₙ₋₁ + $25.
How to get the recursive formula?Here we will have something like an arithmetic sequence, such that the recursive sequence is something like:
aₙ = aₙ₋₁ + d
Where d is the common difference.
We know that the first value (the first amount that she has in her savings account) is $50, so we can write the first term as:
a₁ = $50
Now, each new year (the subindex "n" represents the number of the year) $25 are added to that savings account, then we will have:
a₂ = $50 + $25 = $75
a₃ = $50 + $25 + $25 = $100
And so on..
So the common difference is d = $25, then the recursive relation is:
aₙ = aₙ₋₁ + $25.
Learn more about recursive formulas.
https://brainly.com/question/1275192
#SPJ1
1) a2 - 12a + 35
Help
Answers
Answer:
(a−5)(a−7)
Step-by-step explanation:
factor a2−12a+35
a2−12a+35
The middle number is -12 and the last number is 35.
Factoring means we want something like
(a+_)(a+_)
Which numbers go in the blanks?
We need two numbers that...
Add together to get -12
Multiply together to get 35
Can you think of the two numbers?
Try -5 and -7:
-5+-7 = -12
-5*-7 = 35
Fill in the blanks in
(a+_)(a+_)
with -5 and -7 to get...
(a-5)(a-7)
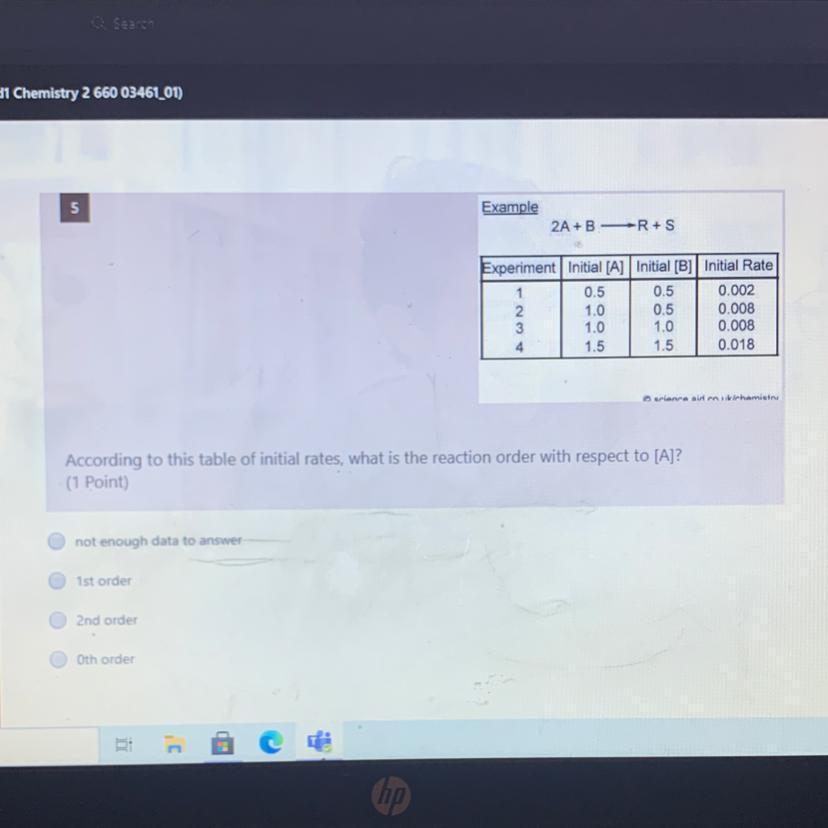
What is the order of the reaction with respect to A?
Answers
From the question, the order of reaction is second order for A
What is the order of reaction?
The rate of a second-order reaction is exactly proportional to the product of the concentrations of the two reactants or to the square of the concentration of a single reactant. Depending on the particular reaction and its stoichiometry, the rate equation for a second-order reaction can take on several shapes.
Studying reaction kinetics, figuring out reaction processes, and planning and optimizing chemical reactions all depend on understanding the order of events.
Learn more about order of reaction:https://brainly.com/question/31609774
#SPJ1
Shelley had 53¢ until she spent 1 quarter. How much money does Shelley have now?
Answers
Answer:
28¢
Step-by-step explanation:
A quarter is 25¢, so 53¢ - 25¢ = 28¢.
Suppose y varies inversely with x, and y = 49 when x = 17
. What is the value of x when y = 7 ?
Answers
Answer:
119 is the value of x when y = 7
Step-by-step explanation:
Since y varies inversely with x, we can use the following equation to model this:
y = k/x, where
k is the constant of proportionality.Step 1: Find k by plugging in values:
Before we can find the value of x when y = k, we'll first need to find k, the constant of proportionality. We can find k by plugging in 49 for y and 17 for x:
Plugging in the values in the inverse variation equation gives us:
49 = k/17
Solve for k by multiplying both sides by 17:
(49 = k / 17) * 17
833 = k
Thus, the constant of proportionality (k) is 833.
Step 2: Find x when y = k by plugging in 7 for y and 833 for k in the inverse variation equation:
Plugging in the values in the inverse variation gives us:
7 = 833/x
Multiplying both sides by x gives us:
(7 = 833/x) * x
7x = 833
Dividing both sides by 7 gives us:
(7x = 833) / 7
x = 119
Thus, 119 is the value of x when y = 7.
Please Explain:
For each pair of the following functions, fill in the correct asymptotic notation among Θ, o, and ω in statement f(n) ∈ ⊔(g(n)). Provide a brief justification of your answers
f(n) = n^3 (8 + 2 cos 2n) versus g(n) = n^2 + 2n^3 + 3n
Answers
The asymptotic notation relationship between the functions \(f(n) = n^3 (8 + 2 cos 2n)\) and \(g(n) = n^2 + 2n^3 + 3n\) is f(n) ∈ Θ(g(n)). Therefore, the growth rates of f(n) and g(n) are primarily determined by the cubic terms, and they grow at the same rate within a constant factor.
To determine the asymptotic notation relationship between the functions \(f(n) = n^3 (8 + 2 cos 2n)\) and \(g(n) = n^2 + 2n^3 + 3n\), we need to compare their growth rates as n approaches infinity.
Θ (Theta) Notation: f(n) ∈ Θ(g(n)) means that f(n) grows at the same rate as g(n) within a constant factor. In other words, there exists positive constants c1 and c2 such that c1 * g(n) ≤ f(n) ≤ c2 * g(n) for sufficiently large n.
o (Little-o) Notation: f(n) ∈ o(g(n)) means that f(n) grows strictly slower than g(n). In other words, for any positive constant c, there exists a positive constant n0 such that f(n) < c * g(n) for all n > n0.
ω (Omega) Notation: f(n) ∈ ω(g(n)) means that f(n) grows strictly faster than g(n). In other words, for any positive constant c, there exists a positive constant n0 such that f(n) > c * g(n) for all n > n0.
Now let's analyze the given functions:
\(f(n) = n^3 (8 + 2 cos 2n)\\g(n) = n^2 + 2n^3 + 3n\)
Since both functions have the same dominant term, we can say that f(n) ∈ Θ(g(n)) because they grow at the same rate within a constant factor. The other notations, o and ω, are not applicable here because neither function grows strictly faster nor slower than the other.
To know more about growth rate,
https://brainly.com/question/33562447
#SPJ11
© A new car cost $14875. Three years later, the insurance company valued it at $10700. Calculate the percentage
reduction in value over the three years.
Answers
Answer: either I don't understand the question or its 72% and I'm fairly certain its 72%
Find the solutions to the following absolute value equation.
Separate multiple answers with a comma.
Provide your answer below:
9 |x-7|+9 = 17
X=
Answers
Answer:
x=71/9, 55/9
Step-by-step explanation:
Pre-SolvingGivenWe are given the absolute value equation 9|x-7| + 9 = 17, and we want to solve the equation for x.
SolvingFirst, we need to isolate the absolute value on one side of the equation.
To do this, we can first subtract 9 from both sides.
9|x-7| + 9 = 17
-9 -9
____________________
9|x-7| = 8
Now, we divide both sides by 9.
|x-7| = 8/9
For absolute value equations, there are two cases; one case is when the expression (or number) that the absolute value expression is equal to is positive, and the other is when it is negative.
This means we need to split the equation into 2 cases.
The first case is when 8/9 (the number the absolute value expression is equal to) is positive.
x - 7 = 8/9
Add 7 to both sides.
x = 71/9
The second case is when 8/9 is negative.
x - 7 = -8/9
Add 7 to both sides.
x = 55/9
The solution is:
x = 71/9, 55/9
The sum of 3 consecutive integers is less than or equal to 15 what is one possible set of three integers to satisfy this inequality hint let n represent the first number so then the next number would be n+1 and so on

Answers
Step 1
Let the first consecutive integer be n
Then the second will be n+1
The third will be n+2
Step 2
Write an inequality for the problem
\(n+n+1+n+2\leq15\)Step 3
Solve the inequality
\(\begin{gathered} 3n+3\leq15 \\ 3n\leq15-3 \\ 3n\leq12 \\ \frac{3n}{3}\leq\frac{12}{3} \\ n\leq4 \end{gathered}\)Step 4
Find the possible set of three integers to satisfy the inequality.
\(\begin{gathered} n=4---\text{ first integer} \\ n+1=4+1=5---\text{ second integer} \\ n+2=4+2=6---\text{ Third integer} \\ \text{check} \\ 4+5+6\leq15 \\ \text{Hence the set of thr}ee\text{ integers are; }\mleft\lbrace4,5,6\mright\rbrace \end{gathered}\)One possible set of three integers that satisfy the inequality is;
{4,5,6}
which phrase describes the variable expression y - 12
Answers
Answer:
The number y decreased by 12.
Step-by-step explanation:
Answer
the answer is b y decreased by 12
Step-by-step explanation:
that is what y-12 is
Solve for x
X-7=-x/2+4
Answers
Answer:
x=7.3
x=\(7\frac{1}{3}\)
x=\(\frac{22}3}\)
just in different form
x - 7 =-x ÷ 2 + 4
x - 7 = \(-\frac{1}{2}\) x + 4
2x - 14 = -x + 8
2x + x = 8 + 14
3x = 22
x=\(\frac{22}3}\)
x=7.3
x=\(7\frac{1}{3}\)
if a 27% is a sale profit , how much profit is in the sale of $4650?
pls explain if u can. thanks!!
Answers
Answer $1,255.50
What is the length of the hypotenuse?
18 cm
6 cm
(not drawn to scale)
360 cm
B 6 10 cm
А
144 cm
D 216 cm

Answers
Answer:
B
Step-by-step explanation:
just use pyth then you'll get the answer
Answer:
B
Step-by-step explanation:
Using Pythagoras' identity in the right triangle
let h be the hypotenuse, then
h² = 6² + 18² = 36 + 324 = 360 ( take the square root of both sides )
h = \(\sqrt{360}\)
= \(\sqrt{36(10)}\)
= \(\sqrt{36}\) × \(\sqrt{10}\)
= 6\(\sqrt{10}\) → B
A circular pond has a radius of 3 feet. What is the approximate distance around the edge of the pond?
Answers
Answer:
C=6π=18.84 ( if π=3.14)
Step-by-step explanation:
distance around the edge of the pond means the circumference of the circle=
C=2πr
C=2π(3)
C=6π=18.84 ( if π=3.14)
The approximate distance around the edge of the pond is 18.84 feet.
Given that, a circular pond has a radius of 3 feet.
What is circumference?The circumference of a circle is the perimeter of the circle. It is the total length of the boundary of the circle. The circumference of a circle is the product of the constant π and the diameter of the circle.
We know that, the circumference of a circle is 2πr.
Now, 2×3.14×3
= 18.84 feet
Hence, the approximate distance around the edge of the pond is 18.84 feet.
Learn more about the circumference here:
https://brainly.com/question/28757341.
#SPJ2
How fast does a 500 grain arrow go?
Answers
Answer:
A 500 grain arrow moving at 260 fps has a kinetic energy of 75.04 ft-lbs and a momentum of . 577 slugs*. A 700 grain arrow moving at 175 fps has a kinetic energy of 47.59 ft-lbs and a momentum of . 544 slugs*.
Write -15y=18x+7 in slope intercept form
Answers
The slope-intercept form of the equation -15y=18x+7 will be y= -1.2x-0.46.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line. If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
It is given that, the equation is -15y=18x+7. We have to write the equation in the slope-intercept form.
The slope-intercept form of the equation is,
y=mx+c
Where, m is the slope and c is the intercept,
-15y=18x+7
y=(-18/15)+(-7/15)
y= -1.2x-0.46
Thus, the slope-intercept form of the equation -15y=18x+7 will be y= -1.2x-0.46.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ1