Answers
After plotting the line of the best fit, the estimated values of a and b are
(30,1.15) and the equation is M = 30L ₊ 1.15
Given, the values of L and M are plotted on the graph.
Then the line of best fit is created on the graph.
A line that most accurately depicts the relationship between data points on a scatter plot is called the line of best fit.
When data points appear to be in a straight line, the line of greatest fit is a straight line.
Therefore, we get the point on the line as (30,1.15)
The equation representing the relation:
M = aL + b
(a,b) from the graph is (30,1.15)
substitute the estimated the values,
M = 30L + 1.15
Hence the required values are estimated and plotted on the graph.
Learn more about Line of best fit here:
https://brainly.com/question/17013321
#SPJ9

Related Questions
pls help I'll give brainliest !!

Answers
Answer:
38 in
Step-by-step explanation:
P=w+w+h+h=18+18+6+6=26+12=38 in
Answer:
48
Step-by-step explanation:
18+18+6+6=48
Find the slope of a line perpendicular to the line whose equation is x + y = 3. Fully
simplify your answer.
Answers
Answer:
To find the slope of a line perpendicular to another line, we need to first find the slope of the given line. The equation of the given line is x + y = 3. We can rewrite this equation in slope-intercept form (y = mx + b) by solving for y: y = -x + 3 So the slope of the given line is -1. To find the slope of a line perpendicular to this line, we know that it will have a slope that is the negative reciprocal of -1, which is 1. Therefore, the slope of a line perpendicular to the line whose equation is x + y = 3 is 1.
Answer: 1
Step-by-step explanation:
The given equation x + y = 3 can be rearranged to slope-intercept form, which is y = -x + 3.
To find the slope of this line, we can see that the coefficient of x is -1. Therefore, the slope of the line is -1.
To find the slope of a line perpendicular to this line, we need to take the negative reciprocal of the slope of the given line.
The negative reciprocal of -1 is 1/1 or simply 1. Therefore, the slope of a line perpendicular to the line x + y = 3 is 1.
Give the limits of integration for evaluating the integral
∭f(r,θ,z)dz r dr dθ
as an iterated integral over the region that is bounded below by the plane z = 0, on the side by the cylinder r=cosθ and on top by the paraboloid z=3r^2.
Answers
Answer:
θ = 0 to θ = 2π, r = 1 to r = -1 and z = 0 to z = 3
Step-by-step explanation:
Since the integration is in cylindrical coordinates, θ is integrated from 0 to 2π.
Since r = cosθ
when θ = 0, r = cos0 = 1
when θ = 2π, r = cos2π = -1
Since the region is bounded below by the plane z = 0, and on the top by the paraboloid z = 3r², z is integrated from z = 0 to z = 3r².
So, when r = 1, z = 3r² = 3(1)² = 3
when r = -1, z = 3r² = 3(-1)² = 3
So, the limits of integration of
∭f(r,θ,z)dz r dr dθ are θ = 0 to θ = 2π, r = 1 to r = -1 and z = 0 to z = 3
Identify the growth factor from the equation

Answers
Answer:
8.21
Step-by-step explanation:
Divide 30 into five parts such that first nad last part are in the ratio 2:3
Answers
To divide 30 into five parts such that the first and last parts are in the ratio of 2:3, we can follow these steps:
1. Determine the ratio between the first and last parts. In this case, it is 2:3.
2. Add the ratio values together to find the total number of parts: 2 + 3 = 5.
3. Divide the total value (30) by the total number of parts (5) to find the value of each part: 30 / 5 = 6.
4. Multiply the value of each part by the respective ratio values to obtain the individual parts:
- First part: 2 * 6 = 12
- Second part: 6
- Third part: 6
- Fourth part: 6
- Last part: 3 * 6 = 18
Therefore, the five parts of 30, with the first and last parts in the ratio of 2:3, are 12, 6, 6, 6, and 18.
Somebody please help meee

Answers
3√2/(√3 - √2) . (√3 - √2)/(√3 - √2)
3√2(√3 - √2)/(3 - 2)
3√2(√3 - √2)
3√6 - 6
3(√6 - 2)
Answer: 3(√6 - 2)
The principal of Fremont High School is putting together a table that lists student attendance at four types of events held at the school last year. How many of the events' total audience members attended musical concerts last year?

Answers
Answer:
Step-by-step explanation:
The answer is 2050
The right triangle on the right is a scaled copy of the right triangle on the lef
Identify the scale factor. Express your answer as a whole number or fraction
in simplest form.
10
10
20
20

Answers
scalar factor= 2, in order to find the scalar factor between two triangle we need to get the ratio between any of thier side of both the triangle on same side
what is scalar factor?
In mathematics, a scalar factor is a numerical value that scales or stretches a vector or a matrix by a certain factor. In other words, a scalar factor is a constant that is multiplied to a given vector or matrix to change its size or magnitude.
In the given question,
In mathematics, a scalar factor is a numerical value that scales or stretches a vector or a matrix by a certain factor. In other words, a scalar factor is a constant that is multiplied to a given vector or matrix to change its size or magnitude.
For instance, if we have a vector v = (x, y, z), then multiplying it by a scalar factor k will result in a new vector kv = (kx, ky, kz), which is stretched or shrunk according to the value of k. Similarly, if we have a matrix A, multiplying it by a scalar factor k will result in a new matrix kA, where each element of A is multiplied by k.
in order to find the scalar factor between two triangle we need to get the ratio between any of thier side of both the triangle on same side
scalar factor= opposite side of bigger triangle / opposite side of smaller triangle
scalar factor= 20/10
scalar factor= 2
To know more about scalar factor , visit:
https://brainly.com/question/17202953
#SPJ1
MY
LAST
QUESTION (NEED HELP ASAP) PLEASE!!!!

Answers
Answer:
The answer is A
Step-by-step explanation:
Substitute t = 3 and t = 6 to determine if the two expressions are equivalent. 3 (2 t + 5) 6 t + 15 Which statements are true? Select the three correct answers. The value of both expressions when t = 3 is 33. The value of both expressions when t = 3 is 23. The value of both expressions when t = 6 is 41. The value of both expressions when t = 6 is 51. The two expressions are equivalent. The two expressions are not equivalent.
Answers
Answer:
If t= 6
3 (2 x 6 + 5) 6 x 6 + 15
3 (12+5) 36 + 15
3 x 17 =51
= 51
The value of both expressio
Step-by-step explanation:
The value of both expressions when t=6 is 51
When t = 3
3(2 x 3 + 5) 6 x 3 + 15
3 (6 +5) 18 + 15
3 x 11 =33
= 33
The value of both expressions when t= 3 is 33
Answer:
A. The value of both expressions when t=3 is 33
D. The value of both expressions when t = 6 is 51.
E. The two expressions are equivalent.
Step-by-step explanation:
I need to know how to do this problem please

Answers
Answer: Total expenses if 3 widgets are produced is $11,018.00
Step-by-step explanation: The variable cost per unit is given by the coefficient of q in the expense function. In this case, the variable cost is $6.00 per widget. To find the variable costs to produce 2 widgets, we simply multiply the variable cost per unit by the number of units produced: Variable costs for 2 widgets = 2 x $6.00 = $12.00 Therefore, the variable costs to produce 2 widgets is $12.00. To find the variable costs to produce q widgets, we simply multiply the variable cost per unit by the number of units produced: Variable costs for q widgets = q x $6.00 = $6q Therefore, the variable costs to produce q widgets is $6q. To find the total expenses if 3 widgets are produced, we can use the expense function and substitute q = 3:E = 6.00 q + 11,000
E = 6.00 (3) + 11,000
E = 18.00 + 11,000
E = 11,018.00 Therefore, the total expenses if 3 widgets are produced is $11,018.00.
What is the value of f(-5) ?

Answers
Answer: 7
Step-by-step explanation:
f(x) = y
f(-5) = y
x = -5
find the value of y at x = -5
and the answer is 7
Which method correctly solves the equation using the distributive property?
-0.2(×-4)= -1.7
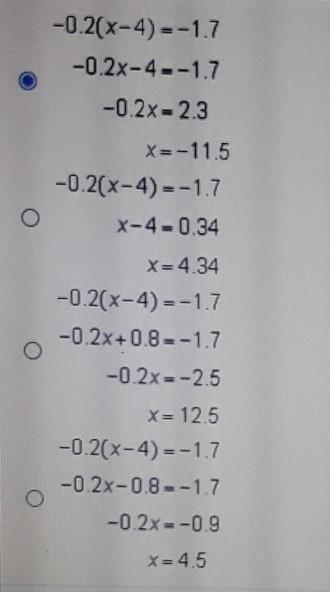
Answers
Answer:
third // C
Step-by-step explanation:
A parallelogram is transformed according to the rule (x, y) → (x, y). Which is another way to state the transformation?
R0, 90°
R0, 180°
R0, 270°
R0, 360°
Answers
Answer:
C. R0, 270°
Step-by-step explanation:
Since one rotation is 90 degrees, hence another way to state the transformation is R0, 270°
What is transformation?A transformation is a technique that is used to change the position of a figure in a xy-plane. These transformation techniques are dilation, reflection, translation, and rotation.
For the transformations process (x, y) ) → (x, y). This shows that the initial coordinate must have rotated 3 times across the x and y-axis
Since one rotation is 90 degrees, hence another way to state the transformation is R0, 270°
Learn more on transformation here: https://brainly.com/question/2689696
To conserve water, many communities have developed water restrictions. The water utility charges a fee of $34, plus an additional $1.36 per hundred cubic feet (HCF) of water. The recommended monthly bill for a household is between $60 and $85 dollars per month. If x represents the water usage in HCF in a household, write a compound inequality to represent the scenario and then determine the recommended range of water consumption. (Round your answer to one decimal place.)
60 ≤ 1.36x − 34 ≤ 85; To stay within the range, the usage should be between 69.1 and 87.5 HCF.
60 ≤ 1.36x − 34 ≤ 85; To stay within the range, the usage should be between 44.1 and 87.5 HCF.
60 ≤ 1.36x + 34 ≤ 85; To stay within the range, the usage should be between 37.5 and 44.1 HCF.
60 ≤ 1.36x + 34 ≤ 85; To stay within the range, the usage should be between 19.1 and 37.5 HCF.
Answers
The compound inequality to represent the scenario is 60 <= 34 + 1.36x <= 85 and the range is 19 to 37.5
How to determine the compound inequality to represent the scenario and then determine the recommended range of water consumption?The given parameters are:
Charges = $34
Rate = $1.36
Recommendation = $60 to $85
The total charge on a HCF is represented as:
Total = Charge + Rate * x
So, we have
Total = 34 + 1.36x
The compound inequality to represent the scenario is then represented as:
60 <= 34 + 1.36x <= 85
Add 34 from the inequality
26 <= 1.36x <= 51
Divide by 1.36
19 <= x <= 37.5
Hence, the compound inequality to represent the scenario is 60 <= 34 + 1.36x <= 85 and the range is 19 to 37.5
Read more about compound inequality at
https://brainly.com/question/1485854
#SPJ1
In order for you to carry a bag on the plane, it must fit inside the carry-on Baggage Check Box. The carry-on Baggage Check Box has dimensions of approximately 22 inches x 14 inches x 9 inches. Your black bag has a height of 18 inches, a depth of 12 inches and a width of 8 inches. Your blue bag has a height of 18 inches, a depth of 15 inches and a width of 10 inches.
What is the volume of the Carry-on Baggage Check Box?
22×14x9= 2772 inches3
What is the volume of the black bag?
What is the volume of the blue bag?
Which bag will definitely fit in the Check Box? Explain.
You notice these two old suitcases stacked in the closet. The smaller suitcase is 25 inches x 8 inches x 9 inches and the larger suitcase is 75 inches x 20 inches x 18 inches.
The bigger suitcase is how many times larger than the smaller suitcase? HINT: You will need to divide on this one.
You decide to use the larger suitcase to transport rectangular prism watermelons back home. The watermelons are about 720 cubic inches. If one of the watermelons is about 10 inches long and 9 inches wide, about how tall would it be? (Hint: V=LxWxH, so plug in 720=10x9xH and solve for H).
If the watermelons are about 720 cubic inches, what is the MAXIMUM amount of watermelons you’ll be able to bring home in your larger suitcase, assuming all you have in the suitcase is the watermelons. (Hint: Divide the larger suitcase volume and the volume of the watermelon).
Answers
1. The volume of the black bag is 1728 cubic inches. 2. The volume of the blue bag is 2700 cubic inches. 3. The black bag will fit in the Check Box. 4. The bigger suitcase is 27 times larger than the smaller suitcase.
What is volume?Volume, which is commonly expressed in cubic units, is the amount of space occupied by a three-dimensional object. By multiplying an object's length, breadth, and height, as well as other formulas depending on the shape of the object, one can get the volume of the thing. Volume is a key concept in many practical applications, including calculating container capacity, constructing structures, and estimating the amount of material required for a construction project. Volume is utilised in many branches of mathematics, science, and engineering.
For the given dimensions of the bags we have:
1. The volume of the black bag is:
18 x 12 x 8 = 1728 cubic inches
2. The volume of the blue bag is:
18 x 15 x 10 = 2700 cubic inches
3. The black bag will definitely fit in the Check Box because its volume of 1728 cubic inches is less than the volume of the Check Box, which is 2772 cubic inches.
4. The ratio of bigger suitcase to smaller suitcase is:
75 x 20 x 18 = 27000 cubic inches
25 x 8 x 9 = 1800 cubic inches
27000 / 1800 = 27
The bigger suitcase is 27 times larger than the smaller suitcase.
5. Now, if the watermelons is about 10 inches long and 9 inches wide, then its height would be:
720 = 10 x 9 x H
720 = 90H
H = 8 inches
The maximum amount of watermelons that can fit are:
27000 / 720 = 37.5 watermelons = 37 watermelons.
Learn more about volume here:
https://brainly.com/question/1578538
#SPJ1
1. In science class, you learned about converting temperatures between degrees Celsius (°C) and Fahrenheit (°F), but recently you could not find a reference with the correct formulas. You then remembered that the relationship between °F and °C is linear.
a. Using this and the knowledge that 32 °F = 0 °C and 212 °F = 100 °C, find an equation that computes Celsius temperature in terms of Fahrenheit; i.e. an equation of the form C = “an expression involving only the variable F.”
b. Analogously, find an equation that computes Fahrenheit temperature in terms of Celsius temperature; i.e. an equation of the form F = “an expression involving only the variable C.”
Answers
The two relations to change the units of temperatueres are:
a) C = (5/9)*(F - 32°)
b) F = (9/5)*C + 32°
How to relate the temperature in Celsius and Fahrenheit?We start knowing that:
32°F = 0°C
212°F = 100°C
Taking the difference we can get the relation:
212°F - 32°F = 100°C - 0°C
180°F = 100°C
1.8°F = 1°C
(9/5)*F = 1°C
Then the relation to go from Farhenheit to Celcius is:
C = (5/9)*(F - 32°)
b) To get the other relation, we just need isolate F in the above one, so we get:
C = (5/9)*(F - 32°)
(9/5)*C = F - 32°
(9/5)*C + 32° = F
Then the other relation is:
F = (9/5)*C + 32°
If you want to learn more about temperature:
https://brainly.com/question/25677592
#SPJ1
Find the measure of angle "T"

Answers
Answer:
T=71 degrees
Step-by-step explanation:
180- 82º-27º=71º
you got this! lmk if you need any more help! <33
t= 71 degrees
Kip walks 5/9 mile in 5/8 hour. What is kips rate of speed? How far can kip walk in one hour?
Answers
Step-by-step explanation:
5/8 hr = 5/9 mile
1 hr = 5/9 ÷ 5/8
= 8/9 mile
Speed = distance / time
= 5/9 mile / 5/8 hr
= 8/9 miles per hr?
The resting heart rate for an adult horse should average about µ = 47 beats per minute with a (95% of data) range from 19 to 75 beats per minute. Let x be a random variable that represents the resting heart rate for an adult horse. Assume that x has a distribution that is approximately normal.
Required:
a. What is the probability that the heart rate is less than 25 beats per minute?
b. What is the probability that the heart rate is greater than 60 beats per minute?
c. What is the probability that the heart rate is between 25 and 60 beats per minute?
Answers
Answer:
a. 0.0582 = 5.82% probability that the heart rate is less than 25 beats per minute.
b. 0.1762 = 17.62% probability that the heart rate is greater than 60 beats per minute.
c. 0.7656 = 76.56% probability that the heart rate is between 25 and 60 beats per minute
Step-by-step explanation:
Empirical Rule:
The Empirical Rule states that, for a normally distributed random variable:
Approximately 68% of the measures are within 1 standard deviation of the mean.
Approximately 95% of the measures are within 2 standard deviations of the mean.
Approximately 99.7% of the measures are within 3 standard deviations of the mean.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean:
\(\mu = 47\)
(95% of data) range from 19 to 75 beats per minute.
This means that between 19 and 75, by the Empirical Rule, there are 4 standard deviations. So
\(4\sigma = 75 - 19\)
\(4\sigma = 56\)
\(\sigma = \frac{56}{4} = 14\)
a. What is the probability that the heart rate is less than 25 beats per minute?
This is the p-value of Z when X = 25. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{25 - 47}{14}\)
\(Z = -1.57\)
\(Z = -1.57\) has a p-value of 0.0582.
0.0582 = 5.82% probability that the heart rate is less than 25 beats per minute.
b. What is the probability that the heart rate is greater than 60 beats per minute?
This is 1 subtracted by the p-value of Z when X = 60. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{60 - 47}{14}\)
\(Z = 0.93\)
\(Z = 0.93\) has a p-value of 0.8238.
1 - 0.8238 = 0.1762
0.1762 = 17.62% probability that the heart rate is greater than 60 beats per minute.
c. What is the probability that the heart rate is between 25 and 60 beats per minute?
This is the p-value of Z when X = 60 subtracted by the p-value of Z when X = 25. From the previous two items, we have these two p-values. So
0.8238 - 0.0582 = 0.7656
0.7656 = 76.56% probability that the heart rate is between 25 and 60 beats per minute
Evaluate 2x + 3y if x =2 and y = 8
Answers
The answer is :
2x2 + 3x8 = 4+24 = 28
The amount of water in a leaky bucket is given by the linear function f(t)=115-3t, where f(t) is in ounces and t is in minutes. Find the amount of water in the bucket after 9 minutes.
←
OA. 88 ounces
OB. 142 ounces
OC. 27 ounces
OD. 112 ounces
Answers
The amount of water in the bucket after 9 minutes is (a) 88 ounces
How to determine the amount of water in the bucket after 9 minutes.From the question, we have the following parameters that can be used in our computation:
f(t)=115-3t
where f(t) is in ounces t is in minutesThis means that
f(t) = 115 - 3t
Also from the question, we have:
The amount of water in the bucket after 9 minutes.
This means that
t = 9
Substitute the known values in the above equation f(t) = 115 - 3t, so, we have the following representation
f(9) = 115 - 3 * 9
Evaluate the products
f(9) = 115 - 27
Evaluate the difference
f(9) = 88
Hence, the amount of water is 88 ounces
Read more about linear equations at
https://brainly.com/question/4074386
#SPJ1
Convert 25°C to Fahrenheit. Use the formula F = (1.8)C + 32°.
58.8°F
102.6°F
77°F
52°F
plz help
Answers
Answer:
77 F
Step-by-step explanation:
F = (1.8)*25 + 32
= 45+32
= 77
Hope this helps!
Answer:
77 degrees Fahrenheit
Step-by-step explanation:
plug 25 into 'C' in the formula
F = 1.8(25) + 32
what is the inverse of g?
g(x) = 3/x+7
Answers
Given function :-
\(\bf \implies g(x) = \dfrac{3}{x}+7\)
To find its reverse , substitute y = g(x) .\(\bf \implies y = \dfrac{3}{x}+7\)
Interchange x and y .\(\bf \implies x = \dfrac{3}{y}+7\)
Solve for y .\(\bf\implies \dfrac{3}{y}= x -7 \\\\\bf\implies y =\dfrac{3}{x-7} \)
Replace y with f-¹(x) .\(\implies\boxed{\red{\bf f^{-1}(x) = \dfrac{3}{x-7} }}\)
Use the information to answer the question. Sabrina walked from her home to the library she stopped to pick up a book, and then she walked home. Sabrina's Walk 2.0- 1.5 Distance from Home (miles) 0.5- 10 20 30 40 50 60 70 80 Time (minutes) Between which times was Sabrina at the brary Enter the answer in the boxes. minutes to minutes

Answers
Answer:
30 minutes to 40 minutes.
Step-by-step explanation:
From the graph attached,
Distance of Sabrina from her home has been given on y-axis and time taken is on x-axis.
Sabrina's walked 2 miles to reach the library in the duration = 30 - 0
= 30 minutes
She stayed at the library from 30 minutes to 40 minutes (Represented by the straight horizontal line).
Then the third segment represents the journey of Sabrina from library to home.
Therefore, Sabrina was at the library between 30 minutes to 40 minutes.
Find the value of h in the parallelogram below.

Answers
The correct answer is h equals 5
x 10xy) + 16x
19 +11z +2 (-2-z)
Answers
Answer:
Don't understand retype your question
Shown below is a wooden six-sided (hexagon) frame. Which of
the following best approximates the slopes of the six line
segments?
O The slopes are approximately -1.4, 0, and 1.4.
O The slopes are approximately -1.7, 0, and 1.7.
O The slopes are approximately -1.8, 1, and 1.4.
O The slopes are approximately -1.7,0, and 1.4

Answers
The slopes are best approximated as: The slopes are approximately -1.7, 0, and 1.7.
How to find the slope between two coordinates?The formula to find the slope between two coordinates is expressed as:
Slope = (y₂ - y₁)/(x₂ - x₁)
The slope of each line above the x-axis are:
Slope 1 = (5 - 0)/(5 - 8)
Slope 1 = -1.7
Slope 2 = (5 - 5)/(5 - (-2))
Slope 2 = 0
Slope 3 = (5 - 0)/(-2 - (-5))
Slope 3 = 5/3 = 1.7
Read more about slope between two coordinates at: https://brainly.com/question/3493733
#SPJ1
I NEED HELP ASAP!
Determine which integers in the set S: {−2, −3, −4, −5} will make the inequality 4p − 7 ≥ 9p + 8 true
S:{−2, −3}
S:{−3, −4}
S:{−4, −5}
S:{−3, −4, −5}
Answers
The integers in the set S: {−2, −3, −4, −5} which would make the inequality 4p − 7 ≥ 9p + 8 true are: S:{−3, −4, −5}
How to determine the integers?In order to determine which integers are true with respect to a solution of the given inequality, we would have to test the given integers by substituting their values into the inequality as follows;
For integers (-2, -3), we have:
4p − 7 ≥ 9p + 8
4(-2) − 7 ≥ 9(-2) + 8
-8 - 7 ≥ -18 + 8
-15 ≥ -10 (False).
For integers (-2, -3), we have:
4p − 7 ≥ 9p + 8
4(-3) − 7 ≥ 9(-3) + 8
-12 - 7 ≥ -27 + 8
-19 ≥ -21 (True).
For integers (-3, -4), we have:
4p − 7 ≥ 9p + 8
4(-3) − 7 ≥ 9(-3) + 8
-12 - 7 ≥ -27 + 8
-19 ≥ -21 (True).
For integers (-3, -4), we have:
4p − 7 ≥ 9p + 8
4(-4) − 7 ≥ 9(-4) + 8
-16 - 7 ≥ -36 + 8
-23 ≥ -28 (True).
For integers (-4, -5), we have:
4p − 7 ≥ 9p + 8
4(-4) − 7 ≥ 9(-4) + 8
-16 - 7 ≥ -36 + 8
-23 ≥ -28 (True).
For integers (-4, -5), we have:
4p − 7 ≥ 9p + 8
4(-5) − 7 ≥ 9(-5) + 8
-20 - 7 ≥ -45 + 8
-23 ≥ -37 (True).
Therefore, -3, -4, and -5 are integers that would make the inequality true.
Read more on inequality here: brainly.com/question/28748540
#SPJ1
Serena estimates that she can paint 60 square feet of wall space every half-hour.write an equation for the relationship with time in hours as the independent variable.can Serena paint 400 square feet of wall space in 3.5 hours?why or why not?
Answers
Answer:x=3.5 x 60
the answer is yes because when she's doing 3.5 hour, and she can do 420 square feet
