Answers
Last one.
Hope this helps.
Related Questions
The mean operating cost per hour for the current production method at S-E Electronics equals $220. A new production method will be implemented if ahypothesis test based on sample data suggests the new method reduces (v. the current method) the mean operating cost per hour.
Required:
a. State the null and alternative hypotheses associated with the test.
b. What is the Type I Error for the test and what are the business consequences of a Type I Error?
Answers
Answer:
H0 : μ = 220
H0 : μ < 220
Rejecting the null when it is actually true
We incorrectly drop a better method.
Step-by-step explanation:
The null hypothesis, H0
H0 : μ = 220
H0 : μ < 220
A type 1 error is committed when a true null hypothesis is incorrectly rejected. This means that we conclude that new method reduces the mean operating cost per hour when in fact it hasn't.
The impact of this on business is that the new method is adopted in place of the old method thinking it works better Than the old method.
if you’re good with probability math 30 please help with questions 33 and 35! real answers only

Answers
Answer: 33) b 34) a 35) none
Step-by-step explanation:
33)
Filling in the Venn Diagram (from Left to right, including outside of circles):
T only = 13
(T ∩ F)only = 6
F only = 21
(T ∩ D) only = 3
T ∩ F ∩ D = 5
(F ∩ D) only = 8
D only = 15
(T ∪ F ∪ D)' = 11
TOTAL = 82
\(P(D'\cap F) = \dfrac{6+21}{13+6+21+3+5+8+15+11}\quad =\large\boxed{\dfrac{27}{82}}\)
34)
Red = 26
Face = 12
Red ∩ Face = 6
Total cards = 52
R ∪ F = R + F - (R ∩ F)
= 26 + 12 - 6
= 32
\(P(R\cup F)=\dfrac{R\cup F}{Total}\quad =\dfrac{32}{52}\quad \rightarrow \quad \large\boxed{\dfrac{8}{13}}\)
35) Note that the total is 34 + 17 + 8 + 3 + 9 + 4 + 5 = 80
I think the teacher made an error, if so, then the answer is "d".
\(P(C) = \dfrac{34+17+3+9}{Total} =\dfrac{53}{80}\quad \bigg(not\ \dfrac{34}{75}\bigg)\qquad \text{This is False.}\\\\\\P(S\cap T)=\dfrac{9+0}{Total}=\dfrac{9}{80}\quad \bigg(not\ \dfrac{12}{75}\bigg)\qquad \text{This is False.}\\\\\\\\P(C\cup T)\cup S = \dfrac{17+9+3+4}{Total}= \dfrac{33}{80}\quad \bigg(not\ \dfrac{38}{75}\bigg)\qquad \text{This is False.}\\\\\\P(C\cup T)\cap S'=\dfrac{34+17+8}{Total}=\dfrac{59}{80}\quad \bigg(not\ \dfrac{59}{75}\bigg)\quad \text{This is False.}\)
if you take away 25 from a number you will be left with two and halftimes 30. what is the number?
Answers
If you take away 25 from (100) you get 75.
70 also equals 2.5*30
Pablo solved the polynomial equations given in the table. Determine whether each polynomial is correct. Select Correct or Incorrect for each equation.
Equation
(b²+7b-9)+(4b-6b²) = -8b² + 14b-9
(4a+6)-(3a²-9a+1)=-3a²+ 13a +5
(12c-8c²)+(5c²- 10c) = -3c²+2c
Answers
The first equation is incorrect.
The second equation is correct.
The third equation is correct.
Let's go through each equation and determine whether it is correct or incorrect:
(b²+7b-9)+(4b-6b²) = -8b² + 14b-9
To determine if this equation is correct, we need to simplify both sides and check if they are equal.
On the left side:
(b²+7b-9)+(4b-6b²) = b² - 6b² + 7b + 4b - 9 = -5b² + 11b - 9
On the right side:
-8b² + 14b - 9
Comparing both sides, we can see that -5b² + 11b - 9 is not equal to -8b² + 14b - 9. Therefore, the equation is incorrect.
(4a+6)-(3a²-9a+1)=-3a²+ 13a +5
Again, we need to simplify both sides of the equation and check if they are equal.
On the left side:
(4a+6)-(3a²-9a+1) = 4a + 6 - 3a² + 9a - 1 = -3a² + 13a + 5
On the right side:
-3a² + 13a + 5
Comparing both sides, we can see that -3a² + 13a + 5 is equal to -3a² + 13a + 5. Therefore, the equation is correct.
(12c-8c²)+(5c²- 10c) = -3c²+2c
Again, let's simplify both sides and compare them.
On the left side:
(12c-8c²)+(5c²- 10c) = 12c - 8c² + 5c² - 10c = -3c² + 2c
On the right side:
-3c² + 2c
Comparing both sides, we can see that -3c² + 2c is equal to -3c² + 2c. Therefore, the equation is correct.
For more such questions on equation visit:
https://brainly.com/question/17145398
#SPJ8
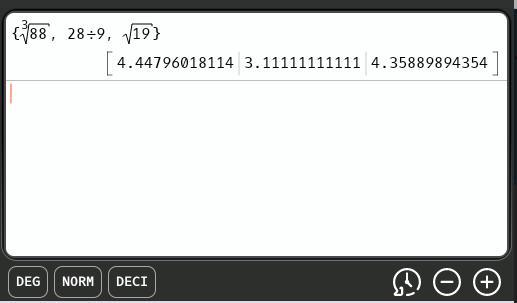
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
Find the variance of the data. 198, 190, 245, 211, 193, 193
bar x=205
Variance(o2)=?
Round to the nearest tenth.

Answers
The variance of the data-set in this problem is given as follows:
σ² = 366.3.
How to obtain the variance of the data-set?The variance of a data-set is calculated as the sum of the differences squared between each observation and the mean, divided by the number of values.
The mean for this problem is given as follows:
205.
Hence the sum of the differences squared is given as follows:
SS = (198 - 205)² + (190 - 205)² + (245 - 205)² + (211 - 205)² + (193 - 205)² + (193 - 205)²
SS = 2198.
There are six values, hence the variance is given as follows:
σ² = 2198/6
σ² = 366.3
More can be learned about the variance of a data-set at https://brainly.com/question/24298037
#SPJ1
What is the surface area of the cone?

Answers
Answer:
V=1/3*pi*radius(to the power of two)*height
Answer: 14 in squared
How do you solve this??
21 a(little 6) b(little 5)
————————————
7 a(little 3) b
Answers
\((21a^6b^5) / (7a^3b)\) simplifies to \(3a^3b^4.\)
To solve this problemWe can use the rules of exponents and simplify the terms with the same base.
Dividing the coefficients: 21 / 7 = 3.
For the variables, you subtract the exponents: \(a^6 / a^3 = a^(^6^-^3^) = a^3.\)
Similarly,\(b^5 / b = b^(5-1) = b^4\).
Putting it all together, the simplified expression is:
\(3a^3b^4.\)
Therefore, \((21a^6b^5) / (7a^3b)\) simplifies to \(3a^3b^4.\)
Learn more about rules of exponents here : brainly.com/question/11975096
#SPJ1
Directions: Solve each system of equations by using substitution. Check your answers.
PLEASE help I have no idea how to do this...

Answers
I'll do the first three problems to get you started.
====================================================
Problem 1
y = -2
4x+6 = -2 ... replace or substitute y with 4x+6
4x = -2-6
4x = -8
x = -8/4
x = -2
Answer: (x,y) = (-2,-2)====================================================
Problem 2
y = -5x-8
3x = -5x-8 .... substitute y with 3x
3x+5x = -8
8x = -8
x = -8/8
x = -1
Use this to find y
y = 3x = 3(-1) = -3
or
y = -5x-8 = -5(-1)-8 = 5-8 = -3
Answer: (x,y) = (-1, -3)====================================================
Problem 3
y = -4x+5
2x-7 = -4x+5
2x+4x = 5+7
6x = 12
x = 12/6
x = 2
Use this to find y
y = -4x+5 = -4(2)+5 = -8+5 = -3
or
y = 2x-7 = 2(2)-7 = 4-7 = -3
Answer: (x,y) = (2, -3)====================================================
Side note:
To check the answers, we plug the coordinates back into the original equations.
For instance, here's what it would look like to check the answer to problem 3.
y = -4x+5
-3 = -4(2)+5 ... plug in (x,y) = (2,-3)
-3 = -8+5
-3 = -3 ... first equation works
y = 2x-7
-3 = 2(2)-7
-3 = 4-7
-3 = -3 ... second equation works
Both equations are true for (x,y) = (2,-3). This verifies the answer to problem 3. The other problems will follow similar steps.
Match each letter to its correct term. Efficiency Unobtainable Impossible Inefficiency Underutilization 1. A 2. B 3. C

Answers
Each letter should be matched to its correct term as follows;
1. A ⇔ Efficiency.
2. B ⇔ Impossible.
3. C ⇔ Inefficiency.
What is a production possibilities curve?In Economics and Mathematics, a production possibilities curve (PPC) can be defined as a type of graph that is typically used for illustrating the maximum and best combinations of two (2) products that can be produced by a producer (manufacturer) in an economy, if they both depend on the following two (2) factors;
Technology is fixed.Resources are fixed.Based on the production possibilities curve shown in the image attached above, we can reasonably infer and logically deduce that each of the letters represent the following terminologies;
A ⇔ Efficiency: it represent points on the production possibilities curve.B ⇔ Impossible: it represent points outside the production possibilities curve.C ⇔ Inefficiency: it represent points on the interior of a production possibilities curve.Read more on production possibilities here: brainly.com/question/26460726
#SPJ1

Consider the line y = 7x-3.
What is the slope of a line parallel to this line?
What is the slope of a line perpendicular to this line?
Answers
Answer:
Gradient of parallel line= 7
Gradient of perpendicular line \( = - \frac{1}{7} \)
Step-by-step explanation:
The equation of the line is already in slope-intercept form (y= mx +c). This means that the coefficient of x is the gradient and the constant -3 is the y-intercept of the line.
y= 7x -3
Gradient= 7
Parallel lines have the same gradient.
Thus, the slope of the line parallel to this line is also 7.
The product of the gradients of 2 perpendicular lines is -1.
(Gradient of perpendicular line)(7)= -1
Gradient of perpendicular line
= -1 ÷7
\( = - \frac{1}{7} \)
Hello! :)
Parallel lines have the same slope.
If one line has a slope of 7, then the line parallel to it has a slope of 7 as well.
Now, perpendicular lines have slopes that are opposite reciprocals. It means we take the slope of one line, make it negative, and flop it over:
\(7\\-7\\-\frac{1}{7}\)
Hope it helps. Feel free to ask me if you have any questions.
~A determined teen
\(MagicalNature\)
Mrs. Lodge is having new floor tiles installed in her kitchen. She is paying the flooring company $170.25 for the tiles and an installation fee of $3.78 per square foot. She receives a total bill of $586.05 for the job. Which equation could be used to find the number of square feet (x) of tile Mrs. Lodge is having installed?
Answers
Referring to the figure, what is the slope of the
line? pls quick

Answers
Answer:
26) 70
27) 12.86 sec
28) 350 feet
Step-by-step explanation:
26) Given points A(0, 0) and B(16, 1120)
slope m = \(\frac{y_2-y_1}{x_2-x_1}\)
\(=\frac{1120-0}{16-0}\\ \\=\frac{1120}{16}\\ \\=70\)
slope = 70
27) eq of a line is :
y = mx + c
y = 70x + c
Since the line passes through A(0,0) substituting the points in the equation,
0 = 70(0) + c
⇒ c = 0
eq of line: y = 70x
given distance is 900 ft
y = distance and x = time
⇒ y = 900
sun in eq,
900 = 70x
⇒ x = 900/70
⇒ x = 12.86
28) time is 5 sec
⇒ x = 5
sub in eq
y = 70(5)
⇒ y = 350
subtract x^2+8x from -3x^2-3x-7.
Answers
Answer: -4x²-11x-7
Step-by-step explanation:
\(-3x^2-3x-7-(x^2+8x)=\\-3x^2-3x-7-x^2-8x=\\-4x^2-11x-7\)
In a warehouse, there are 2 robots that work together. They move in the same direction concurrently, so if one moves North, they both North. The robots will follow any instructions they’re given and will collect any objects they find along the way. They only take instructions by the points of the compass and can only move in 4 directions (N, E, S, W).
For example, if the 2 robots are given the directions: “N, E, S”, then Robot A will collect a ball and Robot B will collect a hat.
Write the directions the robots would need to follow to collect the following objects, remembering that both robots get the same directions, and assuming that for each question they start off in the same (pictured above) positions:
1. Robot A: ball Robot B: ball
2. Robot A: hat, ball Robot B: box, hat
3. Robot A: ball, ball Robot B: hat, ball

Answers
1. For collecting balls by both Robot A and B the direction will be N->E->E
2. For collecting hat and ball by Robot A and box and hat by Robot B, the direction will be N->N->S->E->E
3. For collecting both the balls by Robot A and a hat and ball by Robot B, the direction will be E->E->N
The direction that both Robot A and Robot B can take are N, E, S and W
For Part 1:
Robot A and Robot B need to collect the ball which is in the 2nd row 5th column for Robot A and 4th row 3rd column for Robot B, therefore the direction will be:
=N->E->E
For Part 2:
Robot A needs to collect a hat and ball which are in the 1st-row third column and 2nd row 5th column respectively. Robot B needs to collect a box and a hat which are in the 3rd row 1st column and 4th row 3rd column respectively. Therefore, the direction will be:
= N->N->S->E->E
For Part 3:
Robot A needs to collect both the balls which are in the 3rd-row 4th column and 2nd row 5th column respectively. Robot B needs to collect a hat and a ball which are in the 5th row and 2nd column & 4th row 3rd column respectively. Therefore, the directions will be:
= E->E->N
Learn more about directions:
https://brainly.com/question/1122190
#SPJ1
Use the drop-down menus to complete each statement about the functions f and g.
Note: Exponential functions are of the form f(x) = abx.
The function f is (linear, exponential, neither)
.
Consecutive (differences, quotients)
are (constant, nonconstant )
.
The function g is (options are same for the rest)
.
Consecutive
are
.

Answers
The function f(x) is the linear and the function g(x) is the exponential. Then the equations are f(x) = 6x and g(x) = 3(2)ˣ.
What is a function?A function is a statement, rule, or law that establishes the connection between two variables. In mathematics, functions are everywhere and are necessary for constructing physical connections.
The functions f(x) and g(x).
The table is shown below.
Let the function f(x) be the linear function and the function g(x) be the exponential. Then we have
Then the function f(x) will be
f(x) = mx + c
Then we have
12 = 2m + c
6 = m + c
Then we have
m = 6 and c = 0
Then the equation will be
f(x) = 6x
Then the function g(x) will be
g(x) = abˣ
Then we have
48 = ab⁴
24 = ab³
We have
a = 3 and b = 2
Then the function g(x) will be
g(x) = 3(2)ˣ
More about the function link is given below.
https://brainly.com/question/5245372
#SPJ1
Xian is planning a party at the skating rink. The cost for each person attending is $3. 50 for skate rental and $5. 00 for food. Xian cannot spend more than $300. Which inequality could be used to find the greatest number of people, p, that can attend?.
Answers
The inequality could be used to find the greatest number of people, p, that can attend is 3.5p + 5p ≤ 300.
Here the inequality is that the sum of the cost of rentals and food which is represented by 3.5p and 5p, respectively, must be less than or equal to $300. By solving the inequality we can determine the maximum number of people that can attend the party while staying within Xian's budget.
To solve the inequality, we first subtract 5p from both sides to isolate the 3.5p term. This results in 3.5p≤300-5p. Then we divide both sides by 3.5 to isolate p, which yields p≤85.71. Since we can't have a fractional number of people, we can determine the maximum number of 85 people that can attend the party.
To know more about inequality refer to the link brainly.com/question/30231190
#SPJ4
someone help me please in so confused find the midpoint of (8,-5) and (3,-1)

Answers
We can use the midpoint formula for this given problem.
Let (x1, y1) = (8, -5)
(x2, y2) = (3, -1)
The midpoint formula is:
M = { [(x1 + x2)/ 2] , [(y1 + y2)/ 2] }
M = { [(8 + 3)/ 2] , [(-5 + -1)/ 2] }
M = { [(11)/ 2] , [(-6)/ 2] }
M = (5.5, -3)
So the midpoint of points A and B is: (5.5, -3), where the x-coordinate is 5.5, and the y-coordinate is -3.
All you need to do is plot the point on the graph.
Multiply or divide. write fractions in simplest form.
2/3 * (-2 1/4) * (-1 1/2)
i really need help with this problem! i will mark you brainliest :)
Answers
Step-by-step explanation:
Okay so, let's turn these into decimals first (rounded to nearest 2 thousandths).
2/3 = 0.66666 (repeating), to the nearest 2 thousandths would be 0.66.
-2 1/4 = -9/4 = -2.25
-1 1/2 = -3/2 = -1.5
then we set up the problem
0.66 × -2.25 × -1.5 = 2.2275 rounded 2.22 as an improper fraction 111/50 and that cannot be simplified any smaller.
What is the distance between point A and point B?

Answers
Answer:
13 units
Step-by-step explanation:
absolute value helps but
itd just be 7-(-6) = 13
Find the distance between the point (5,12) and the line y = 5x + 12 (rounded to the nearest hundredth).
A. 1.36 units
B. 2.19 units
C. 4.81 units
D. 4.90 units
Answers
The distance between the point (5,12) and the line y = 5x + 12 is 4.90 units
How to find the distance between a point and a line?
If a point P with the coordinates (x₁, y₁), and we need to know its distance from the line represented by ax + by + c = 0
Then the distance of a point from the line is given by the formula:
d = (ax₁ + by₁ + c) / √(a² + b²)
Given: the point (5,12) and the line y = 5x + 12. The line can be written as
5x-y+12 = 0. Thus:
x₁ = 5, y₁ = 12, a = 5, b = -1, c = 12. Substitute these into the formula:
d = (ax₁ + by₁ + c) / √(a² + b²)
d = (5×5 + (-1×12) + 12) / √(5² + (-1)²)
d = 25/√26 = 4.90 units
Therefore, the distance between the point and the line is 4.90 units. Option D is the answer
Learn more about distance between a point and a line on:
https://brainly.com/question/18276750
#SPJ1
Choose the expression that is equivalent to the expression n − n + n − n.
Answers
A flat-screen television has a diagonal length of 40 inches. The length of the screen is 175% of its height. What is the length, in inches, of the screen?
Answers
The length of the flat-screen television is approximately 40.01 inches.
Let's assume that the height of the flat-screen television is "h" inches.
From the problem statement, we know that the length of the screen is 175% of its height.
Mathematically, we can write:
Length = 1.75 x Height
We can substitute the value of "h" in this equation to find the length of the screen:
Length = 1.75 x h
Now, we also know that the diagonal length of the screen is 40 inches. Using the Pythagorean, we can write:
(Length)² + (Height)² = (Diagonal)²
Substituting the values we have, we get:
(1.75h)² + h² = (40)²
Expanding and simplifying:
3.0625h² = 1600
Dividing both sides by 3.0625:
h² = 522.24
Taking the square root of both sides (and ignoring the negative root since we're dealing with lengths):
h = 22.86 inches
Now we can use the equation we derived earlier to find the length:
Length = 1.75 x h
Length = 1.75 x 22.86
Length = 40.01 inches (rounded to two decimal places)
For similar questions on length
https://brainly.com/question/28322552
#SPJ11
Evaluate mº - n2 for m = 2 and n = -1.
Answers
Answer:
\( \boxed{ \tt{0}}\)
Step-by-step explanation:
\(if \: mº - {n}^{2} \: for \: m = 2 \: and \: n = -1. \\ {2}^{0} - ( { - 1)}^{2} = 1 - (1) = 0\)
Line d passes through points (10, 8) and (2, 1). Line e is perpendicular to d. What is the slope of line e? Simplify your answer and write it as a proper fraction, improper fraction, or integer.
Answers
The slope of line e is -8/7, which represents a proper fraction
The slope of line e, which is perpendicular to line d, can be determined using the concept that the slopes of perpendicular lines are negative reciprocals of each other.
First, let's find the slope of line d using the given points (10, 8) and (2, 1). The slope (m) is calculated using the formula:
m = (y2 - y1) / (x2 - x1)
Plugging in the values, we have:
m = (1 - 8) / (2 - 10)
= (-7) / (-8)
= 7/8
Since line e is perpendicular to line d, its slope will be the negative reciprocal of 7/8. The negative reciprocal is obtained by flipping the fraction and changing its sign. Therefore, the slope of line e is -8/7.
Hence, the slope of line e is -8/7, which represents a proper fraction.
For more such answers on slope of line
https://brainly.com/question/16949303
#SPJ8
Find f\left(x+3\right)f(x+3) given the function: f\left(x\right)=-5x+3f(x)=−5x+3
Answers
Answer:
-5x-12
Step-by-step explanation:
Given f(x) = -5x+3, to get f(x+3), we are going to replace x in f(x) with x+3 as shown;
f(x) = -5x+3
f(x+3) = -5(x+3)+3
f(x+3) = -5x-15+3
f(x+3) = -5x-12
Hence the function f(x+3) is -5x-12
Write a cosine function that has an amplitude of 3, a midline of 2 and a period
Answers
Answer:
f(x) = 3 cos (2Pi / period value ; x )+ 2
or see answer using 2 as the period see answer in bold below.
Step-by-step explanation:
cosine function amplitude of 3 is A = 3
The period is used to find B
You need to show period value as the denominator and work out from there with 2PI as a function numerator to show as 2pi / period can be a data angle
C is the adding value.
Acos (Bx) + C
A = 3
Bx = 2 pi / period
C = + 2
However f 2 is also the period found
then we just plug in 2 to above formula
f(x) = 3 cos (2Pi / 2 ; x )+ 2
f(x) = 3cos (x pi) + 2

* 9. Two fifths of what number is 120?
2/5
Answers
Answer:
300
Step-by-step explanation:
120 ÷ 2/5 = 300
Let X represent the number we are looking for
2/5 x X=120
2/5X=120
Divide both sides by 2/5
X= 300
L
A bakery sells 6 bagels for $3.99 and 4 muffins for $2.29. What is the total cost in dollars of 2 dozen bagels and 12 muffins? *
PLEASE ANSWER ASAP
Answers
The following are the annual incomes (in thousands of dollars) for 8 randomly chosen, U.S. adults employed full-time.
44, 44, 54, 54, 65, 39, 54, 44
Send data to calculator
(a) What is the mean of this data set? If your answer is not an
integer, round your answer to one decimal place.
(b) What is the median of this data set? If your answer is not
an integer, round your answer to one decimal place.
(c) How many modes does the data set have, and what are
their values? Indicate the number of modes by clicking in the
appropriate dircle, and then indicate the value(s) of the
mode(s), if applicable.
0
Zero modes
one mode:
Two modes:
Answers
Answer:
(a) To find the mean of the data set, sum up all the values and divide by the total number of values.
44 + 44 + 54 + 54 + 65 + 39 + 54 + 44 = 398
Mean = 398 / 8 = 49.75
Rounded to one decimal place, the mean of this data set is 49.8.
(b) To find the median of the data set, i need to arrange the values in ascending order first:
39, 44, 44, 44, 54, 54, 54, 65
The median is the middle value in the sorted data set. In this case, we have 8 values, so the median is the average of the two middle values:
(44 + 54) / 2 = 98 / 2 = 49
Rounded to one decimal place, the median of this data set is 49.0.
(c) To determine the modes of the data set, identify the values that appear most frequently.
In this case, the mode refers to the value(s) that occur(s) with the highest frequency.
From the data set, i see that the value 44 appears three times, while the value 54 also appears three times. Therefore, there are two modes: 44 and 54.
