Part 2
Use your answer above (and more differentiation/integration) to now express the following function as a power series (centered at x = 0).
g(x) = 1/(9+x)³
Answers
Therefore , the solution of the given problem of function comes out to be g(x) (-1)ⁿ (n+2)!/n! (9ⁿ⁻²) xⁿ.
What is function?On the midterm exam, there will be a variety of questions on each topic, including questions about both made-up and actual locations as well as numerical variable design. a diagram showing the relationships between different elements that cooperate to create the same result. A service is composed of numerous distinctive components that cooperate to create distinctive results for each input.
Here,
With x = 0, we can use the formula for the geometric series to represent the function g(x) = 1/(9+x)3 as a power series:
=> 1 / (1 - t) =∑ (n = 0 to n) t
where |t| 1 and t is some integer.
In this instance, we have:
=> g(x) = 1/(9+x)³ = \((1/9)^{3}\) \((1+(-x/9))^{-3}\)
So, using the above calculation and the value of t = -x/9, we can write:
=> G(x) = (1/9)3 n(x/9) (n=0 to infinite)
If we condense this phrase, we get:
=> (n=0 to infinite) = g(x) \((-1)^{n}\) (n+2)!/n! (\(9^{n-2}\)) \(x^{n}\)
Thus, the power series expansion for g(x) with the origin at x = 0 is as follows:
=> (n=0 to infinite) = g(x) (-1)ⁿ (n+2)!/n! (9ⁿ⁻²) xⁿ
To know more about function visit:
brainly.com/question/28193995
#SPJ1
Related Questions
What’s the inequality?

Answers
Answer:
1/2 (one over two)
Step-by-step explanation:
when you are finding an a slope, or inequality as you wrote here, you are using formula: y/x ( y over x )
the graph dotes show how they are moving 2 to the right(x) and 1 up(y), so it’s 1/2!
Simplify 4x²y + 12z² + 6x²y – 2z.
10x²y + 12z² - 2z
10x²y + 14z²
20x²yz²
10x²y + 10z²
Answers
Answer:
Group the like terms together:
4x²y + 6x²y + 12z² - 2z
Simplify:
10x²y + 12z² - 2z
The simplified expression is 10x²y + 12z² - 2z.
Step-by-step explanation:
Answer:
The simplified expression is 10x²y + 12z² - 2z
Step-by-step explanation:
To simplify the expression, we combine like terms, which are terms that have the same variables raised to the same powers. In this case, we have two terms with the variable 4x²y and two terms with the variable -2z. We can combine these like terms by adding their coefficients:
4x²y + 6x²y = 10x²y
-2z + (-2z) = -4z
So the expression simplifies to:
10x²y + 12z² - 4z
We can further simplify this expression by combining the terms with the variable z:
12z² - 4z = 4z(3z - 1)
Therefore, the final simplified expression is:
10x²y + 4z(3z - 1)
We can also write this expression as:
10x²y + 12z² - 2z
which is the answer provided.
The matrix below represents a system of equations.
2 -1 -3 -20
-2
-6 6 -4
0
3 -2 -9
Which matrix represents
1/R2+R3 → R3?

Answers
The first matrix.
What is a matrix?A matrix is an array of numbers arranged in rows and columns.
Analysis:
1/2R2 +R3 to R3
means divide row 2 by 2 and add it to row 3 to form row 3 of the new matrix.
1/2R2 = -1 -3 3 -2
R3 = 0 3 -2 -9
1/2R2 + R3 = -1 0 1 -11
In conclusion, the matrix with the above operation is the first matrix.
Learn more about matrix: brainly.com/question/1821869
#SPJ1
Your favorite dog groomer charges according to your dog's weight. If your dog is 10 pounds or under, the groomer charges $30. If your dog is between 10 and 35 pounds, she charges $40. If your dog is 35 pounds or over, she charges $1.25 per pound. You have three dogs. Max weighs 25 pounds, Sally weighs 8 pounds and Goliath weighs 80 pounds. How much will your total cost be if you get all three dogs groomed?
Answers
Answer:
$170
Step-by-step explanation:
Sally costs 30
Max costs 40
Goliath costs 80(1.25) = 100
add them up
$170
Needing help on my geometry final, I have been in and out of the hospital, any help is appreciated.
1. In the first figure, what is the area of DEF? Show your work.
2. In his suitcase, Jack has 3 shirts, 2 pants, 3 pairs of socks, and 2 pairs of shoes, how many unique ways can Jack get dresed? Show your work.
3. In the second figure, what is the area of quadrilateral QRST if QS = 18 and RT = 24? Show your work.
4. Suppose you draw one card from a deck of 52 cards. A standard deck of cards has 4 of each type of card, so the deck contains 4 queens and 4 kings. What is the possibility that the card is a king or a queen? Explain.
5. In the last figure, suppose you throw two fair number dices. What is the probability that the sum of the results of the throw if 4,5,or 6? Show your work



Answers
Answer:
1. area = 1/2bh = (1/2)(21)(18) = 189 yd²
2. 3x2x3x2 = 36 different ways
3. area of kite = (1/2)(18)(24) = 216 units²
4. 8:52 or reduced, 2:13
5. Sorry, this is not my strong point
Step-by-step explanation:
1. The slant height of a cone is 5cm and the radius of its base is 3cm. Find correct to the nearest
whole number the volume of the cone (A) 48cm3 (B) 47cm3 (C) 38cm3 (D)13cm3
Answers
The volume of the cone is 13 cm³. option D
How to determine the volumeTo determine the volume of the cone, we have that;
The formula for calculating the volume of a cone is expressed as;
Volume = (1/3)πr ²√(L ² - r ²).
Such that;
r is the radiusL is the slant heightSubstitute the values, we have;
Volume = 1/3 × 3.14 ² × √(25 - 9)
Find the squares, we get;
Volume, V = 1/3 × 9. 86 × √16
Find the square root
Volume, V = 1/3 × 9.86 × 4
Volume, V = 13 cm³
Learn more about volume at:
#SPJ1
4th question!!! Can anyone help me ?
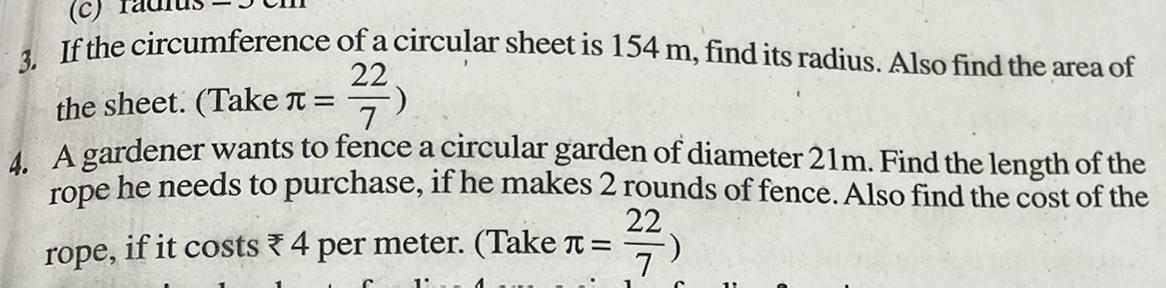
Answers
Cost=66*2*4=176//
Answer:
₹528Step-by-step explanation:
Length of Fence
Circumference = 2πr or πdπd22/7 x 21 m22 x 3 m66 m2 rounds = 66 x 2 = 132 mCost
₹4 x 132₹528Question 2 of 10 Suppose a population consists of 5000 people. Which of the following numbers of members of the population being surveyed could result in a sample statistic but not a parameter ? A. Both 50 and 5000 B. 50 C. Neither 50 nor 5000 D. 5000
Answers
Out of the population being surveyed, the one that could result in a sample statistic but not a parameter is; B: 50
What is the Sample Statistic?
A sample statistic is a piece of information you get from a fraction of a population.
A parameter is a number describing a whole population (e.g., population mean), while a statistic is a number describing a sample (e.g., sample mean).
Now, we are told that a population consists of 5000 people. This means that the sample statistic could be the sample mean which could be 50 but certainly not 5000 as the sample statistic can't be same as the population.
Read more about Sample Statistic at; https://brainly.com/question/7301139
#SPJ1
find the quotient with explain
a. 16.5 ÷ 10 =
b. 16.5 ÷ 100 =
Answers
Answer:
\(16.5 \div 10 = 1.65 \\ 16.5 \div 100 = 0.165\)
Help.............
..

Answers
The part of the expression which represents the discounted price before tax is x-35.
The given expression is 0.12x+(x-35).
What is an expression?An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division.
a) The part of the expression represents the discounted price before tax is x-35
b) The part of the expression represent the amount of sales tax in dollars is 0.12x
Hence, the part of the expression which represents the discounted price before tax is x-35.
To learn more about an expression visit;
https://brainly.com/question/28170201.
#SPJ1
Example # 2:
Find
Za
for the confidence level 90%.
2
Example # 3:
Find 2, for the confidence level 99%.
Answers
Answer:
(a) 1.645
(b) 2.5758
Step-by-step explanation:
The complete question is: Find Z(\(\alpha\)/2) for the confidence level 90% and for the confidence level 99%.
Firstly, as we know that \(\alpha\) represent the level of significance, i.e;
Level of significance = 1 - confidence level
(a) We are given the confidence level of 90%, so;
Level of significance = 1 - 90%
= 1 - 0.90 = 0.10 or 10%
Now, \(Z_(_\frac{\alpha}{2}_)\) = \(Z_(_\frac{0.10}{2}_)\) = \(Z_(_0_._0_5_)\)
This means that we have to look for a critical value in the z table at a 5% level of significance which gives us a value of 1.645.
(a) We are given the confidence level of 99%, so;
Level of significance = 1 - 99%
= 1 - 0.99 = 0.01 or 1%
Now, \(Z_(_\frac{\alpha}{2}_)\) = \(Z_(_\frac{0.01}{2}_)\) = \(Z_(_0_._0_0_5_)\)
This means that we have to look for a critical value in the z table at a 0.5% level of significance which gives us a value of 2.5758.
Which of the following is true of protecting classified data?
Answers
True statement for Protecting classified data is classified material must be appropriately marked.
Classified information being transmitted from one commission office to another shall be protected with a classified document cover sheet and hand delivered by an appropriately cleared person to another appropriately cleared person.
Classified information is material that a government body deems to be sensitive information that must be protected. Access is restricted by law or regulation to particular groups of people with the necessary security clearance and need to know, and mishandling of the material can incur criminal penalties.
Data classification is broadly defined as the process of organizing data by relevant categories so that it may be used and protected more efficiently. Data classification involves tagging data to make it easily searchable and trackable.
To know more about classified data here
https://brainly.com/question/29629794
#SPJ4
help me
doing this questions..

Answers
Answer:
{a} {b} {c} {ab} {ac} {bc} {abc}
pls help it'd be appreciated

Answers
Answer:
option A
Step-by-step explanation:
∠WPS +∠OPW = 180 {straight line}
∠WPS +110 = 180
∠WPS = 180 - 110
∠WPS = 70°
∠RWQ + ∠QWT +∠TWU = 180 {straight line}
∠RWQ + 60 + 50 = 180
∠RWQ + 110 = 180
∠RWQ = 180 - 110
∠RWQ= 70°
∠PWU + ∠USP + ∠ WPS = 180 {angle sum property of triangle}
∠PWU + 40 + 70 = 180
∠PWU + 110 = 180
∠PWU = 180 - 110
∠PWU = 70°
Answer:
A
Step-by-step explanation:
∠WPS +∠OPW = 180 (adj angles on a str line)
∠WPS +110 = 180
∠WPS = 180 - 110
= 70°
∠RWQ + ∠QWT +∠TWU = 180 (adj angles on a str line)
∠RWQ + 60 + 50 = 180
∠RWQ + 110 = 180
∠RWQ = 180 - 110
= 70°
∠PWU + ∠USP + ∠ WPS = 180 (adj angles on a str line)
∠PWU + 40 + 70 = 180
∠PWU + 110 = 180
∠PWU = 180 - 110
= 70°
In the given figure AB = AC, BAD = 50 and AD = AE. find the value of x

Answers
Answer:
\(x=25^o\)
Step-by-step explanation:
Angle sum of a triangle: \(< A + < B+ < C=180^o\\\)
Types of Triangles: Isosceles, Equilateral, Scalene
Given AB = AC are two sides of the big triangle, then ΔABC is Isosceles.
Isosceles triangles are defined to have two equal sides and two equal angles (opposite the congruent(equal) sides).
Also, since ABC is defined as a triangle, BC is a straight line, a.k.a., it is a \(180^o\) angle. As the image shows, the line, AD creates a right angle on one side, therefore it creates a right angle(\(90^o\)) on the other side.
Back to Isosceles Triangles, AD = AE means ΔADE is isosceles and <ADE = <AED
Using the Angle sum formula of a triangle, you can fill in <A, <B, and <C with the following:
<A=\(50^o\)
<B=<C=y [This is because <ADE = <AED]
\(50^o+2y=180^o\\2y=130^o\\y=65^o\)
Now, this means that <ADE=\(65^o\) and <ADC =\(90^o\)
<x is better seen as <EDC
<EDC+<ADE=<ADC
Since we know <ADE is 65 and <ADC is 90, we can plug in these to the formula above.
\(x+65^o=90^o\\x=25^o\)
Activity
You have also set up a card game in which a player picks a card from a standard deck of 52 cards. The player wins if these two events occur together: E1, in which the card drawn is a black card, and E2, in which the card drawn is a numbered card, 2 through 10.
Question 1
What is the probability of getting a black card and a numbered card? Calculate the probabilities P(E1) and P(E2) as fractions.
Answers
The probability of getting a black card and a numbered card is 9/26.
To calculate the probability of getting a black card (E1), we need to determine the number of black cards in a standard deck of 52 cards.
There are 26 black cards in total, which consist of 13 spades (black) and 13 clubs (black).
Therefore, the probability of drawing a black card (P(E1)) is:
P(E1) = Number of favorable outcomes / Total number of possible outcomes
P(E1) = 26 / 52
Simplifying this fraction, we get:
P(E1) = 1/2
So the probability of drawing a black card is 1/2.
To calculate the probability of drawing a numbered card (E2), we need to determine the number of numbered cards (2 through 10) in a standard deck.
Each suit (spades, hearts, diamonds, clubs) contains one card for each numbered value from 2 to 10, totaling 9 numbered cards per suit.
Therefore, the probability of drawing a numbered card (P(E2)) is:
P(E2) = Number of favorable outcomes / Total number of possible outcomes
P(E2) = 36 / 52
Simplifying this fraction, we get:
P(E2) = 9/13
So the probability of drawing a numbered card is 9/13.
To calculate the probability of both events occurring together (getting a black card and a numbered card), we multiply the individual probabilities:
P(E1 ∩ E2) = P(E1) × P(E2)
P(E1 ∩ E2) = (1/2) × (9/13)
Simplifying this fraction, we get:
P(E1 ∩ E2) = 9/26
Therefore, the probability of getting a black card and a numbered card is 9/26.
For such more questions on probability
https://brainly.com/question/25839839
#SPJ8
Ty bought a new computer for $499. This brand depreciates at a rate of 12% of the original price per year. The value y of Ty's computer, x years after he purchased it, is found using an equation in the form y = mx + b. What is the approximate value of m?
Answers
Answer:
the approximate value of m is -0.12, indicating that the value of Ty's computer decreases by 0.12 (or 12%) each year.
Step-by-step explanation:
o express this depreciation rate as a slope in the equation y = mx + b, we need to determine how much the value changes (the "rise") for each year (the "run").
Since the value decreases by 12% per year, the slope (m) would be -12%. However, we need to express the slope as a decimal, so we divide -12% by 100 to convert it to a decimal:
m = -12% / 100 = -0.12
help!!!!! this ends in 12 minutes Find the value of x. The diagram is not to scale. Given: RS , ST, MZRTS - 5x - 18. mZSTU- 6x T O 18 108 © 20 23

Answers
Given Data:
\(\begin{gathered} RS\cong ST \\ \angle RTS=5x-18 \\ \angle STU=6x \end{gathered}\)Using the property of linear pair,
\(\begin{gathered} \angle RTS+\angle STU=180 \\ 5x-18+6x=180 \\ 11x=198 \\ x=18 \end{gathered}\)Thus, option (A) is the correct answer.
A complex shape combined frim a square and rectangle b=6, c=8, and d=12 what is the area of this complex figure?
Answers
The area of the complex figure is 132 square units
How to determine the area
From the information given, we have that the composite shape is a combination of a:
SquareRectangleThe formula for area of a square is given as:
Area = a ²
Where 'a' is the length of it side
Area = 6²
Area of square = 36 square units
The formula for area of a rectangle is given as:
Area = width × length
Area = 8 × 12
Area of rectangle = 96 square units
Area of the complex figure = Area of square + area of rectangle
= 36 + 96
= 132 square units
Thus, the area of the complex figure is 132 square units
Learn more about area here:
https://brainly.com/question/25292087
#SPJ1
six slips of paper, each containing a different one of the numbers 3,4,5,6,7,8 and 10 are placed in a hat. then two of the slips are drawn at random
Answers
The probability of drawing two slips of paper containing numbers that are the lengths of two sides of a triangle in the (3,4,5) family is 1/50.
The (3,4,5) family of triangles is a set of triangles that are similar to the triangle with side lengths 3, 4, and 5. In particular, the sides of any triangle in the (3,4,5) family must satisfy the Pythagorean theorem, i.e., the sum of the squares of the two shorter sides must equal the square of the longest side.
We can start by listing all the possible pairs of numbers that can be drawn from the hat
(3,4), (3,5), (3,6), (3,7), (3,8), (3,10)
(4,5), (4,6), (4,7), (4,8), (4,10)
(5,6), (5,7), (5,8), (5,10)
(6,7), (6,8), (6,10)
(7,8), (7,10)
(8,10)
Out of these 20 possible pairs, we need to count the pairs that satisfy the conditions for being lengths of two sides of a triangle in the (3,4,5) family. For any such triangle, the longest side must be either 5 or 10. Therefore, we can split the pairs into two groups
Pairs that include 5: (3,4), (5,6), (5,8), (5,10)
Pairs that include 10: (6,8), (7,10), (8,10)
For a pair to be the lengths of two sides of a triangle in the (3,4,5) family, the sum of the squares of the two shorter sides must equal the square of the longest side. We can check this condition for each of the pairs in the two groups
Pairs that include 5
(3,4): not a valid triangle
(5,6): not a valid triangle
(5,8): the sum of the squares of the two shorter sides is 5^2 + 8^2 = 89, which is not equal to 10^2
(5,10): the sum of the squares of the two shorter sides is 3^2 + 4^2 = 25, which is equal to 5^2
Pairs that include 10
(6,8): the sum of the squares of the two shorter sides is 6^2 + 8^2 = 100, which is equal to 10^2
(7,10): not a valid triangle
(8,10): the sum of the squares of the two shorter sides is 4^2 + 8^2 = 80, which is not equal to 10^2
Therefore, out of the 20 possible pairs, only 2 pairs satisfy the conditions for being lengths of two sides of a triangle in the (3,4,5) family. The probability of drawing one of these pairs is 2/20 = 1/10.
Once the first number is drawn, there are only 5 slips of paper left in the hat, and only one of them is the other side of the triangle, so the probability of drawing the second number is 1/5. Therefore, the probability of drawing two numbers that are the lengths of two sides of a triangle in the (3,4,5) family is (1/10) × (1/5) = 1/50.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Which of the following sets of ordered pairs does not satisfy a linear function?
(2, 5), (3, 7), (4, 9), (5, 11), (6, 13)
(2, 6), (3, 9), (4, 12), (5, 15), (6, 18)
(2, 5), (4, 9), (6, 13), (7, 15), (9, 17)
(2, 6), (4, 8), (6, 10), (8, 12), (10, 14)
Answers
Answer:
(2, 6), (4, 8), (6, 10), (8, 12), (10, 14)
Can someone answer these

Answers
Answer:
1) 3.401244 ft^3
2) 708.75
Step-by-step explanation:
1) take the cube root of the volume (gets you one side of the cube), divide it by 100, then cube that.
2) square the scale factor (3/4), and multiply the area by that number.
1. Given that cosθ≈0.646 where θ is in quadrant IV, find the values of sinθ and tanθ to the nearest thousandth
a. sinθ=−0.763; tanθ=−1.181
b. sinθ=−0.763; tanθ=−0.847
c. sinθ=0.763; tanθ=0.847
d. sinθ=0.763; tanθ=1.181
2. Terran’s running rate is 4 miles per hour faster than her walking rate. She can run 21 miles in the same amount of time it takes her to walk 9 miles. What are her walking and running rates in miles per hour? Write and solve a rational equation to answer the question. Let x be Terran’s walking rate
a. 21/x+4=9/x; Terran walks at 2 miles per hour and runs at 6 miles per hour.
b. 21/x=9/x−4; Terran walks at 7 miles per hour and runs at 10 miles per hour.
c. 21/x=9/x−4; Terran walks at 4 miles per hour and runs at 8 miles per hour.
d. 21/x+4=9/x; Terran walks at 3 miles per hour and runs at 7 miles per hour.
Answers
Answer:
d.) sinθ=0.763; tanθ=1.181
c. 21/x=9/x−4; Terran walks at 4 miles per hour and runs at 8 miles per hour.
Step-by-step explanation:
Given that:
θ is in the IV quadrant (All is positive) that is sin, cos and tan are all positive.
Cosθ = 0.646
Θ = Cos^-1(0.646)
θ = 49.75930
Hence,
Tanθ = tan(49.75930) = 1.1816365 = 1.182
Sinθ = sin(49.75930) = 0.7633373 = 0.763
2.)
Let
Walking rate = x mph
Running rate = x + 4 mph
21 miles run time = 9 miles walk time
Recall :
Time = distance / speed or rate
21 / (x + 4) = 9 / x
Cross multiply :
21 * x = 9(x + 4)
21x = 9x + 36
21x - 9x = 36
12x = 36
x = 36 /12
x = 4 mph = walking rate
Running rate = x + 4 = 4 + 4 = 8 mph
z(y+y); use y=3, and z=3
Answers
Answer:
\( \boxed{ \bold{ \huge{ \boxed{ \sf{18}}}}}\)
Step-by-step explanation:
Given, y = 3 , z = 3
\( \sf{z(y + y)}\)
Plug the value of y and z
⇒\( \sf{3(3 + 3)}\)
Add the numbers : 3 and 3
⇒\( \sf{3 \times 6}\)
Multiply the numbers : 3 and 6
⇒\( \sf{18}\)
Hope I helped!
Best regards! :D
I need help with this

Answers
Answer:
65*
Step-by-step explanation:
All angles in a triangle = 180 degrees.
I got my answer by adding 60°+35°+80° and ended up with 175°. In quick math, you can just add 6+8=14 and add the zero so it would be 140 then add 35 which basically you just need to add 3+4=7 then add the zero once again making the answer a 170 and then just add the leftover 5 you got from the 35.
Which number line represents the solution to the inequality −7x − 13 ≥ 8?




Answers
Answer:
The first picture (x≤-3)
Step-by-step explanation:
A water hose used one-half of a gallon of water every second. If Vanessa need to fill up 2 gallon sized containers, how many seconds would it take? (Will give brainliest to whoever answers first)

Answers

A genetic experiment with peas resulted in one sample of offspring that consisted of 440 green peas and 155 yellow peas.
a. Construct a 95% confidence interval to estimate of the percentage of yellow peas.
b. Based on the confidence interval, do the results of the experiment appear to contradict the expectation that 25% of the offspring peas would be yellow?
Answers
The 95 percent confidence interval is (0.20, 0.32).
a. We can construct a 95% confidence interval to estimate the percentage of yellow peas as follows:
Let p = proportion of yellow peas = 155/595 = 0.26
Sample size = n = 595
Standard error = SE = √(p × (1-p) / n) = √(0.26 × (1-0.26) / 595) = 0.03
95% confidence interval = p ± 1.96 × SE
= 0.26 ± 1.96 × 0.03
= 0.26 ± 0.06
So, the 95% confidence interval is (0.20, 0.32).
b. Yes, the results of the experiment appear to contradict the expectation that 25% of the offspring peas would be yellow, as the 95% confidence interval does not include the expected value of 0.25.
Therefore, the 95 percent confidence interval is (0.20, 0.32).
To learn more about the confidence interval visit:
https://brainly.com/question/14041846.
#SPJ1
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
Answer the question with an algebraic expression.
The perimeter of a square is m meters. How long, in centimeters, is each side of the square?
Answers
The length of the square in centimetres in algebraic expression is 25m
How to find the side length of a square?The perimeter of a square is m meters.
The length of the each side of the square in centimetres can be represented in an algebraic expression as follows:
Therefore,
perimeter of a square = 4l
where
l = side lengthTherefore,
m = 4l
where
m = perimeter of the squarel = m / 4 meters.
Therefore, the side length of the square in centimetres is as follows:
1 meters = 100 cm
m / 4 meters = ?
cross multiply
length of the square in meters = m / 4 × 100
length of the square in meters = 100m / 4
length of the square in meters = 25m
learn more on square here: https://brainly.com/question/13379880
#SPJ1