On a coordinate plane, 2 triangles are shown. The first triangle has points A (negative 1, negative 2), B (negative 4, negative 2), C (negative 1, negative 4). The second triangle has points A prime (1, 2), B prime (4, 2), C prime (1, 4). What rule describes the rotation about the origin? (x, y) → How many degrees was the figure rotated about the origin?
Answers
9514 1404 393
Answer:
(x, y) ⇒ (-x, -y)180°Step-by-step explanation:
Each image point has its signs reversed from the pre-image point.
(x, y) ⇒ (-x, -y) . . . . describes the rotation
Rotation from the third quadrant (A) to the first quadrant (A') is a rotation of 180°.
Answer:
3rd and 2nd option
Step-by-step explanation:
Related Questions
Compare the rates of change of the following table and graph. x y 1 -4 2 -8 3 -12 4 -16 A. The rate of change of the table is greater than the rate of change of the graph. B. There is not enough information to determine the rates of change. C. The rate of change of the table is equal to the rate of change of the graph. D. The rate of change of the graph is greater than the rate of change of the table.
Answers
The average rate of change between -1 and 3 is 9.
The Given graph is not a linear graph, but a curve. More specifically, this is a cubic function, a type of polynomial function.
In this case, it would be more appropriate to find the average rate of change, since the selected points might make a line, but the function as a whole is not linear. Let's say we wish to find the average change of rate in the interval -1, 3, meaning to find the average rate of change from x = -1 to x =3 .
. Before we apply the formula, we locate the output: The coordinates are (-1, 9) and (3, 45).
Calculate the difference between the output values:
Δy=45−9=36.
Calculate the difference between the input values:
Δx=3−(−1)=4.
Finally, find the ratio between the change in output to the change in the input:
Δy/Δx
=36/4
=9
In this example, the average rate of change between -1 and 3 is 9.
Learn more about average rate of change at:
https://brainly.com/question/24313700
#SPJ1
Model the data using an exponential function f(x) = Abx.
x 0 1 2
f(x) 100 90 81
Answers
We can start by using the given data points to create a system of equations:
When x = 0, f(x) = 100
100 = Ab^0
100 = A
When x = 1, f(x) = 90
90 = Ab^1
90 = Ab
When x = 2, f(x) = 81
81 = Ab^2
We can use the first equation to solve for A and substitute that value into the second equation:
90 = Ab
90 = 100b
b = 0.9
Now we can substitute the values of A and b into the third equation to solve for A:
81 = Ab^2
81 = 100(0.9)^2 A = 100(0.81)
A = 81
Therefore, the exponential function that models the data is:
f(x) = 100(0.9)^x
or
f(x) = 81(0.9)^x
If product of two numbers=384HCF=8,2cm=?
Answers
Answer:
96 and 288
Step-by-step explanation:
So, we need to find 2 numbers such that their sum is 8 and they do not have common factor (Relatively prime). Both these numbers will be divisible by 48 but there would be no other common divisor (after dividing by 48).
Such order independent pairs are (1,7) and (3,5).
Difference between them would be (7–1)*48=6*48 and (5–3)*48=2*48 respectively.
The differences are 6*48=288 and 2*48=96.
We have found difference without finding numbers.
Ans.: 96 and 288
p.s.: The number pairs (again order neutral) would be (48, 336) and (144, 240)
Difference for 48 and 336 add up to 384, their HCF is 48. These two numbers match the conditions. Their difference is 288.
Difference of 144 and 240 add up to 384, their HFC is 48 (the numbers are 48*3 and 48*5, common factor is 48 and no other common factor for 3 and 5; 48 is HCF). The difference is 96.
find the equation of a line that is parallel to this line and passes through the point (-3,1)

Answers
Answer:
Two possible equations:
Point-slope form is \(y-1=-\frac{2}{3} (x+3)\)
Slope-Intercept form is \(y=-\frac{2}{3}x+-1\)
Step-by-step explanation:
So to start we need to know what makes a line parallel. In an equation we know that for lines to be parallel they must have the same slope(\(m\)).
Then, we need to know the slope-intercept form of an equation. The point slope form is \(y-y1=m(x-x1)\) where \(m\) is the slope of the line and \(y1\) and \(x1\) represent the point on the graph. This is the equation we'll use for the line.
So now that we understand what we need to find, we need to find the slope of the existing line. To do this we use the equation \(m=\frac{y2-y1}{x2-x1}\). We can plug in the points (-2,3) and (1,1) on the graph to get \(m=\frac{1-3}{1+2}\). When we simplify this we get \(m=-\frac{2}{3}\) so we know our slope is \(-\frac{2}{3}\). Lastly, all we need to do is plug the slope and the new point into our point slope equation to get \(y-1=-\frac{2}{3} (x+3)\).
If you needed to go further and put this into slope-intercept form, you could solve the equation for y to get \(y=-\frac{2}{3}x+-1\)
Is d=2t portional or non portional?
Answers
What is the equation of the line that is parallel to the line defined by the equation y = 3x−7 and goes through the point (4, 2)?
Answers
Answer:
\(y-2=3(x-4)\)
Step-by-step explanation:
Pre-SolvingWe are given a line contains the point (4, 2).
We also know that the line is parallel to y= 3x - 7.
We want to write the equation of this line.
Parallel lines have the same slopes.
First, let's find the slope of y = 3x - 7.
3 is in the place of where m (the slope) is, so that means it is the slope of that line.
It is also the slope of the line whose equation we want to write.
The equation of the line can be written in three ways:
Slope-intercept form, which is y=mx+b, where m is the slope and b is the y-intercept. Standard form, which is ax+by=c, where a, b, and c are free integer coefficients. a and b cannot be 0, and a is usually non-negative as well. Point-slope form, which is \(y-y_1=m(x-x_1)\), where m is the slope and \((x_1, y_1)\) is a point.All of these ways are valid, but for this problem, let's write the equation in point-slope form, as it is the easiest.
SolvingSubstitute 3 as m in \(y-y_1=m(x-x_1)\).
\(y-y_1=3(x-x_1)\)
Now, substitute 4 as \(x_1\) and 2 as \(y_1\).
\(y-2=3(x-4)\)
Topic: parallel and perpendicular lines
See more: https://brainly.com/question/7699889
A rectangular paperboard measuring 33 inches long and 24 inches wide has a semicircle cut out of it, as shown below. Find the area of the paperboard that remains. Use the value 3.14 , and do not round your answer. Be sure to include the correct unit in your answer.
Answers
Answer: 565.92 square inches.
Step-by-step explanation:
To find the area of the paperboard that remains, we need to subtract the area of the semicircle from the area of the rectangle.
The rectangle has a length of 33 inches and a width of 24 inches, so its area is:
A_rect = length x width
A_rect = 33 in x 24 in
A_rect = 792 sq in
To find the area of the semicircle, we need to first find its radius. The diameter of the semicircle is the same as the width of the rectangle, which is 24 inches. So, the radius is:
r = 1/2 x diameter
r = 1/2 x 24 in
r = 12 in
The area of the semicircle is:
A_semicircle = 1/2 x pi x r^2
A_semicircle = 1/2 x 3.14 x 12^2
A_semicircle = 1/2 x 3.14 x 144
A_semicircle = 226.08 sq in
To find the area of the paperboard that remains, we subtract the area of the semicircle from the area of the rectangle:
A_remaining = A_rect - A_semicircle
A_remaining = 792 sq in - 226.08 sq in
A_remaining = 565.92 sq in
Therefore, the area of the paperboard that remains is 565.92 square inches.
A $40 autographed and framed poster of the Spice Girls goes up in price to $50. What is the percent of increase in the price?
Answers
Answer: it went up 25%
Step-by-step explanation: if it would have went up 50%, that would be $20, meaning it would be $60. It is 25% and it is half of 50% and half of $20 is $10 equaling $50
A $40 autographed and framed poster of the Spice Girls goes up in price to $50. What is the percent of increase in the price?
=
25% increase
Find the volume of the solid.

Answers
Answer:
64cm³
Step-by-step explanation:
( 4 x 4 x 4) cm x cm x cm
What is the solution to the equation below?
3(x - 4) = 5x - 6
x = -3
x=3/4
x = 1
x = 9
Answers
Answer:
15=39; not equivalent
Step-by-step explanation:
replace x with 9 and solve using pemdas on each side to see if each side is equivalent
If a game consists of picking a number from a bag of beans numbered 2, 2, 3, 4, and 5 and flipping a coin, which probabilities are equivalent?I. P(2 and head)II. P(even and tail) III. P(odd and tail) A) I and IIB) I and IIIC) II and IIID) none of the above

Answers
Answer:
B) I and III
Explanation:
Given:
• A bag of beans numbered 2, 2, 3, 4, and 5.
,• A coin
To determine which probabilities are equivalent, we calculate the probabilities in I, II, and III below,
Part I
\(\begin{gathered} P(selecting\text{ a bean numbered 2)}=\frac{2}{5} \\ P(flipping\; a\; head\text{)}=\frac{1}{2} \\ \implies P(2\text{ and head)}=\frac{2}{5}\times\frac{1}{2}=\frac{1}{5} \end{gathered}\)The probability of picking a 2 and flipping a head is 1/5.
Part II
\(\begin{gathered} P(selecting\text{ an even nu}mbered\; bean\text{)}=\frac{3}{5} \\ P(flipping\; a\; tail\text{)}=\frac{1}{2} \\ \implies P(even\text{ and tail)}=\frac{3}{5}\times\frac{1}{2}=\frac{3}{10} \end{gathered}\)The probability of picking an even numbered bean and flipping a tail is 3/10.
Part III
\(\begin{gathered} P(selecting\text{ an odd nu}mbered\; bean\text{)}=\frac{2}{5} \\ P(flipping\; a\; tail\text{)}=\frac{1}{2} \\ \implies P(odd\text{ and tail}=\frac{2}{5}\times\frac{1}{2}=\frac{1}{5} \end{gathered}\)The probability of picking an odd-numbered bean and flipping a tail is 1/5.
The equivalent probabilities are I and III. (Option B is correct).
if D equals 4x + 10 e f equals 2x - 1 + d f equals 9 x - 15 find DF
Answers
Answer:
4x+10+2x-1=9x-15;
6x+9=9x-15;
6x-9x=-15-9;
-3x=-24;
3x=24;
from which
x=24:3=8
Then:
DF=9x-15=(9×8)-15=72-15=57
Was this helpful
What steps are used to solve the equation? g – 8 = 14 Complete the statements. First, both sides of the equation. The solution of the equation is . Check the solution by substituting for g and simplifying.
Answers
Answer:
g=22
Step-by-step explanation:
add 8 to both sides
g-8=14
g-8+8=14+8
g=14+8
g=22
The solution of expression g - 8 = 14 is,
⇒ g = 22
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The equation is,
⇒ g - 8 = 14
Now, We can simplify as,
⇒ g - 8 = 14
Add 8 both side,
⇒ g - 8 + 8 = 14 + 8
⇒ g = 22
Thus, The solution of expression g - 8 = 14 is,
⇒ g = 22
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ3
Write an algebraic expression for the phrase 6 times Z
Answers
Answer:
6z
Step-by-step explanation:
Makayla spent $29.99 plus 8.875% tax and also tipped 15% at the car wash. How much did she spent?
(Discount, tax, extra money paid, money saved, and final price can be included)
Answers
Answer:
37.1501125
Step-by-step explanation:
29.99+23.875÷100×29.99 amount then tax+tip divided by 100 ×amount
Points A, B, C, and D lie on circle M. Line segment BD is
a diameter. The measure of arc CD equals the measure
of arc DA.
M
D
B
A
D
What is the measure of angle ADM?
O22.5°
30.0⁰
45.0°
67.5°
Answers
The measure of angle ADM is 45.0°, as the intercepted arc AD is congruent to arc CD.
To find the measure of angle ADM, we need to consider that angle ADM is an inscribed angle and its measure is half the measure of the intercepted arc AD.
Given that the measure of arc CD equals the measure of arc DA, it means that these arcs are congruent.
Therefore, the intercepted arcs AD and CD have equal measures.
Since angle ADM is an inscribed angle intercepting arc AD, the measure of angle ADM is half the measure of arc AD.
Therefore, the measure of angle ADM is 45.0°, as the intercepted arc AD is congruent to arc CD.
for such more question on measure of angle
https://brainly.com/question/25716982
#SPJ8
What is the volume of this shape to the nearest tenth

Answers
What's 10.08 rounded to the nearest one?
Answers
Answer:
10
Step-by-step explanation:
5
Select the correct answer.
Tom gets $12 off a box of chocolates that had an original price of $48. What percentage is the discount?
OA.
12%
OB.
25%
Ос.
50%
OD
60%
Reset
Next
Answers
Answer:
B
Step-by-step explanation:
12 is 1/4 of 48 so when you take $12 off $48 you take 1/4 of 25% away
Answer The Question for Brainliest

Answers
Answer:
turn it 90 degrees, hope this helps
Step-by-step explanation:
Answer:
so go to the 120 degree line and make sure the line is straight across from zero and thin dray a line going from 120 down to the bottom of where the zero is
Step-by-step explanation:
8 groups of ___ hundredths is 0.32
Answers
Answer:
the answer is 0.4 The reason is because 0.4 x8=0.32
Step-by-step explanation:
Which inequality represents the situation described below?
The distance, d, is less than 200 miles.
A. d ≥ 200
B. d > 200
C. d ≤ 200
D. d < 200
Answers
Hello!
The distance, d, is less than 200 miles.
B. d > 200
A land mass is roughly in the shape of a rectangle whose perimeter is 1280 miles. the width is 120 miles less than the length find the length and the width.
HELP!!!!
Answers
As part of a competition, Diego must spin around in a circle 6 times and then run to a
tree. The time he spends on each spin is represented bys and the time he spends
running is r. He gets to the tree 21 seconds after he starts spinning. If it takes Diego 1.2
seconds to spin around each time, how many seconds did he spend running?
Answers
Answer:
It took him 13.8 sec to run
Step-by-step explanation:
Time to spin 6 times can be represented mathematically by "6 s". Then the total time it took him to get to the tree (which must be the addition of the time spinning plus the time running) is:
6 s + r = 21 sec
since each spin takes him 1.2 sec, then we have:
6 (1.2 sec) + r = 21 sec
7.2 sec + r = 21 sec
r = 21 sec - 7.2 sec
r = 13.8 sec
Put these groups of numbers starting with the smallest 1.506, 1.06, 1.501, 1.605
Answers
1.501
1.506
1.605
Hope this helps
A campus survey states that 40% of students ride the bus if there are 300 students how many ride the bus?
Answers
Answer: 180 students
Step-by-step explanation:
10%=30
30x4=120
Select ALL the correct answers.
For ΔABC, which two relationships are true?
An Image of a right-angle triangle BAC with B at the right angle. With an angle of (90 minus theta).
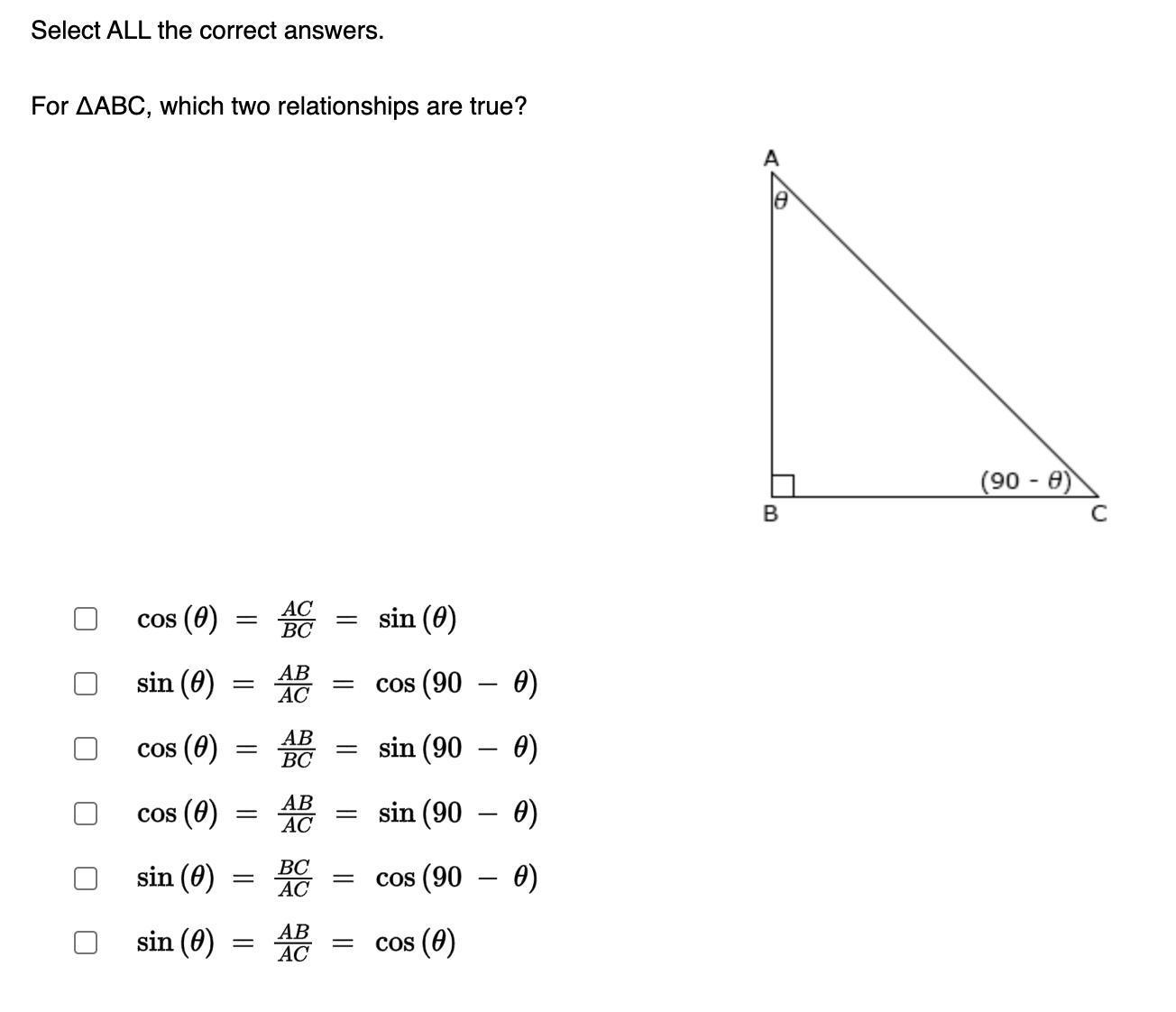
Answers
Answer:
Step-by-step explanation:
An Image of a right-angle triangle BAC with B at the right angle. With an angle of (90 minus theta).Refers to the attachment given below

What is the sine of 0?
(Need help)

Answers
The angle of sinθ between the horizontal vector (1, 0) and the slant vector (15/17, -8/17) is sin⁻¹(8/17), which is approximately 29.11 degrees.
To find the angle of sinθ between a horizontal vector and a slant vector, we can use the dot product formula:
a · b = |a| |b| cos(θ)
where a and b are vectors, |a| and |b| are their magnitudes, and theta is the angle between them.
In this case, the horizontal vector is (1, 0) and the slant vector is (15/17, -8/17).
The magnitude of the horizontal vector is 1, and the magnitude of the slant vector is:
|b| = sqrt((15/17)² + (-8/17)²) = sqrt(225/289 + 64/289) = sqrt(289/289) = 1
The dot product of the two vectors is:
a · b = (1)(15/17) + (0)(-8/17) = 15/17
So we have:
15/17 = (1)(1) cos(θ)
cos(θ) = 15/17
To find sin(θ), we can use the trigonometric identity:
sin²(θ) + cos²(θ) = 1
sin²(θ) = 1 - cos²(θ) = 1 - (15/17)² = 64/289
Taking the square root of both sides, we get:
sin(theta) = sqrt(64/289) = 8/17
To learn more about the vectors;
brainly.com/question/13188123
#SPJ1
what is the slope of the line through (-1 2) and (-3 -2)
Answers
Answer:
m=2
Step-by-step explanation:
Answer:
slope = 2
Step-by-step explanation:
(x₁ , y₁) = (-1 , 2) & (x₂ , y₂) = (-3 , -2)
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\\\= \frac{-2-2}{-3-[-1]}\\\\= \frac{-4}{-3+1}\\\\= \frac{-4}{-2}\\\\= 2\)
Suppose a normal distribution has a mean of 26 and a standard deviation of
4. What is the probability that a data value is between 27 and 28? Round your
answer to the nearest tenth of a percent.
A. 10.3%
B. 9.3%
C. 11.3%
D
12.13%

Answers
Answer:
D,p
Step-by-step explanation:
whattttttt ,why is there no option in D
The Probability that a data value is between 27 and 28 is 9.3%.
What is Probability?
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 to 1,
Here, mean of the data is 26
P(0 ≤ x - μ ≤ σ/2) = 0.195
P(0 ≤ x - μ ≤ σ/4) = 0.0987
P(σ/4 ≤ x - μ ≤ σ/2) = 0.093
Thus, the Probability that a data value is between 27 and 28 is 9.3%.
Learn more about Probability from:
https://brainly.com/question/11234923
#SPJ2