Need help ASAP with answering this question

The median of X is 1;  P(X > 2) = 0; P(one observation < 2 and the other > 2) = P(X < 2) * P(X > 2) = 0 * 0 = 0; Var(X) is approximately 0.33; E(X) is 1 and  the value of q such that P(X < q) = 0.95 is 1.9.

(a) To find the median of X, we need to find the value of x for which the cumulative distribution function (CDF) equals 0.5.

Since the PDF is given as f(x) = 1/2 for 0 < x < 2 and 0 otherwise, the CDF is the integral of the PDF from 0 to x.

For 0 < x < 2, the CDF is:

F(x) = ∫(0 to x) f(t) dt = ∫(0 to x) 1/2 dt = (1/2) * (t) | (0 to x) = (1/2) * x

Setting (1/2) * x = 0.5 and solving for x:

(1/2) * x = 0.5;  x = 1

Therefore, the median of X is 1.

(b) To find P(X > x), we need to calculate the integral of the PDF from x to infinity.

For x > 2, the PDF is 0, so P(X > x) = 0.

Therefore, P(X > 2) = 0.

(c) To find the probability that one observation is less than 2 and the other is greater than 2, we need to consider the possibilities of the first observation being less than 2 and the second observation being greater than 2, and vice versa.

P(one observation < 2 and the other > 2) = P(X < 2 and X > 2)

Since X follows a continuous uniform distribution from 0 to 2, the probability of X being exactly 2 is 0.

Therefore, P(one observation < 2 and the other > 2) = P(X < 2) * P(X > 2) = 0 * 0 = 0.

(d) The variance of X can be calculated using the formula:

Var(X) = E(X²) - [E(X)]²

To find E(X²), we need to calculate the integral of x² * f(x) from 0 to 2:

E(X²) = ∫(0 to 2) x² * (1/2) dx = (1/2) * (x³/3) | (0 to 2) = (1/2) * (8/3) = 4/3

To find E(X), we need to calculate the integral of x * f(x) from 0 to 2:

E(X) = ∫(0 to 2) x * (1/2) dx = (1/2) * (x²/2) | (0 to 2) = (1/2) * 2 = 1

Now we can calculate the variance:

Var(X) = E(X²) - [E(X)]² = 4/3 - (1)² = 4/3 - 1 = 1/3 ≈ 0.33

Therefore, Var(X) is approximately 0.33.

(e) The expected value of X, E(X), is given by:

E(X) = ∫(0 to 2) x * f(x) dx = ∫(0 to 2) x * (1/2) dx = (1/2) * (x²/2) | (0 to 2) = (1/2) * 2 = 1

Therefore, E(X) is 1.

(f) The value of q such that P(X < q) = 0.95 can be found by solving the following equation:

∫(0 to q) f(x) dx = 0.95

Since the PDF is constant at 1/2 for 0 < x < 2, we have:

(1/2) * (x) | (0 to q) = 0.95

(1/2) * q = 0.95

q = 0.95 * 2 = 1.9

Therefore, the value of q such that P(X < q) = 0.95 is 1.9.

Learn more about cumulative distribution function here:

https://brainly.com/question/30402457

#SPJ11

Answer:

yes its 50

Step-by-step explanation:

if you need an explanation let me know!

Answer:

Step-by-step explanation:

I think its 5 correct me if im wrong sorry little bit rsusty at math since last year

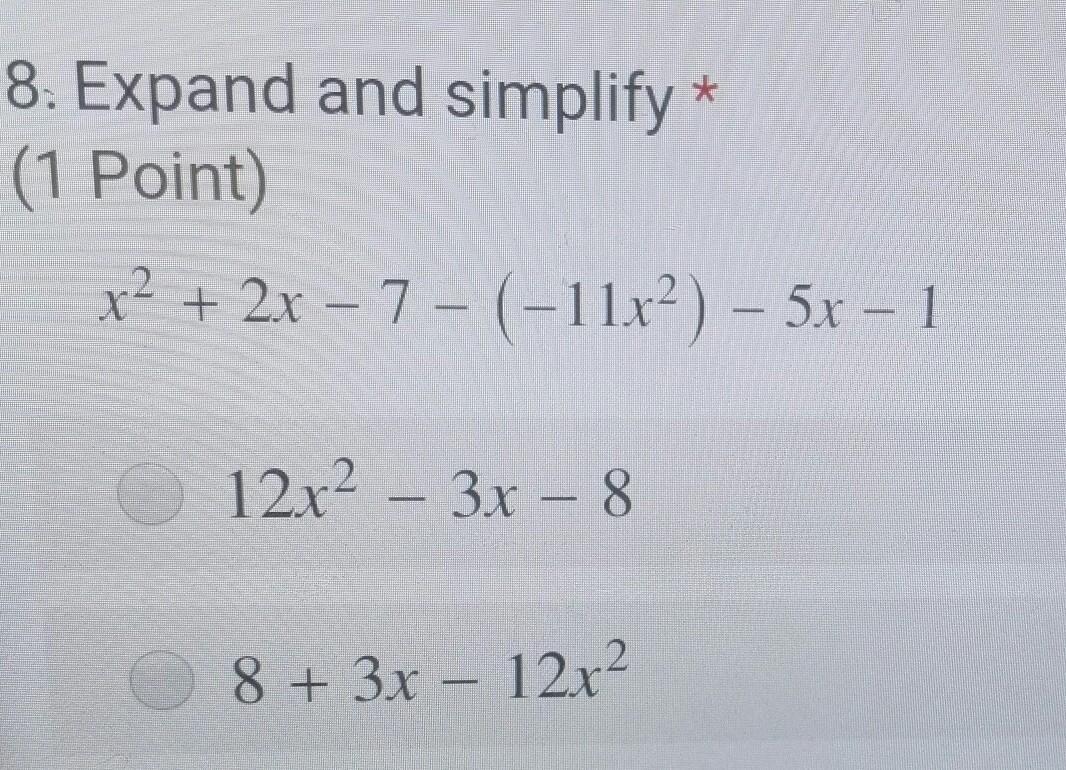
Answer:

Step-by-step explanation:

x2 + 2x - 7 + 11x2 - 5x - 1

Solving like terms

12x2 - 3x - 8

Answer:

y = 5.00000

x = 0.50000

The range of x are;

1. x < -30

2. x > 8

3. x > 15

4. x < -2

A relationship between two expressions or values that are not equal to each other is called 'inequality.

1. -130 > 50x +20

-130-20> 50x

-150 > 50x

-150/50 > x

-30 > x

x < -30

2. -8(x-3) < -40

-8x +24< -40

collect like terms

-8x < -64

x > -64/-8

x > 8

3. 2x - 22 > 8

collect like terms

2x > 30

divide both sides by 2

x > 30/2

x > 15

4. -35 < -5(x+9)

-35 < -5x -45

collect like terms

10 < -5x

-2 > x

x < -2

learn more about inequality from

https://brainly.com/question/24372553

#SPJ1

SUV was detected exceeding the posted speed limit of 60 km/hr, 40 kilometers would she have traveled if she was driving 80 km/hr for half an hour.

Given that an SUV was detected exceeding the posted speed limit of 60 km/hr. We need to calculate how many kilometers would she have traveled if she was driving 80 km/hr for half an hour.

Using the formula,

s = v.t

Where s = Distance

           v = Velocity

            t = time

In this scenario, the velocity of the SUV is given as 80 km/hrt = 0.5 hrs

The distance she will travel at 80 km/hr in 0.5 hrs will be; s = 80 x 0.5s = 40 km

Therefore, the SUV would have traveled 40 kilometers if she was driving 80 km/hr for half an hour.

To learn more about speed: https://brainly.com/question/13943409

#SPJ11

The point prevalence of brilliance at the end of Week 1 is 0.08 or 8%.

The point prevalence of brilliance at the end of Week 2 is 0.17 or 17%.

The point prevalence of brilliance at the end of Week 3 is 0.33 or 33%.

Using person-weeks as denominator, the incidence of brilliance over the course of the 10-week course is 0.017 or 1.7%

In epidemiology context, brilliance can be calculated through calculating point prevalence, cumulative incidence, and incidence rate. The provided data table can be used to determine the point prevalence, incidence, and incidence rate of brilliance among PHE 450 students. So, the calculations of point prevalence, cumulative incidence, and incidence rate based on the provided data are as follows:

The point prevalence of brilliance at the end of Week 1 can be calculated by the following formula; Point prevalence = Total number of existing cases at a given time ÷ Total population at that time

Student #8 was the only existing case of brilliance at the beginning of Week 1, so the point prevalence of brilliance at the end of Week 1 is; Point prevalence = 1 ÷ 12 = 0.08 or 8%.

The point prevalence of brilliance at the end of Week 2 can be calculated by the following formula; Point prevalence = Total number of existing cases at a given time ÷ Total population at that time

Student #3 and Student #8 were existing cases of brilliance at the beginning of Week 2, so the point prevalence of brilliance at the end of Week 2 is; Point prevalence = 2 ÷ 12 = 0.17 or 17%.

The point prevalence of brilliance at the end of Week 3 can be calculated by the following formula; Point prevalence = Total number of existing cases at a given time ÷ Total population at that time

Student #3, #4, #6, and #8 were existing cases of brilliance at the beginning of Week 3, so the point prevalence of brilliance at the end of Week 3 is; Point prevalence = 4 ÷ 12 = 0.33 or 33%.

The incidence of brilliance can be calculated by the following formula; Incidence = Total number of new cases ÷ Total person-weeks of observation

Student #5 and Student #7 developed brilliance during the 10-week course, so the incidence of brilliance over the course of the 10-week course is; Incidence = 2 ÷ 120 = 0.017 or 1.7%.

To know more about denominator refer here:

https://brainly.com/question/931030#

#SPJ11

Answer:

Alex has 3x dollars and an extra 15 dollars in his coat pocket. He buys a new Nike shoe for 84 dollars. How much money did Alex spend that was not in his pocket.

Step-by-step explanation:

Answer:

Part A: Word problem

Maria went to the store and purchased some books for her book club. Each book cost $3, and she also bought some bookmarks at $15 each. Maria's total purchase, including tax, amounted to $84. If Maria bought x books, write an equation to represent the situation.

Part B: Solution

To solve the equation 3x + 15 = 84, we need to isolate the variable x on one side of the equation.

Step 1: Subtract 15 from both sides of the equation to eliminate the constant term on the left side:

3x + 15 - 15 = 84 - 15

3x = 69

Step 2: Divide both sides of the equation by 3 to isolate x:

3x/3 = 69/3

x = 23

So, the solution to the equation is x = 23.

Part C: Explanation

In the given equation 3x + 15 = 84, the variable x represents the number of books Maria purchased. The equation states that the cost of x books at $3 each, represented by 3x, plus the cost of $15 for bookmarks, totals to $84. Thus, the value of x represents the number of books Maria bought in this scenario. In the solution, x = 23, it means Maria purchased 23 books for her book club.

Step-by-step explanation:

u · v is approximately 31.62. To compute u · v, we first need to find the unit vector v in the direction of u. This is done by dividing u by its magnitude ||u||, which is the square root of the sum of the squares of its components:

||u|| = sqrt(3^2 + (-315)^2 + 24^2) = sqrt(99810)

So the unit vector v is given by:

v = u/ ||u|| = (3/sqrt(99810))i - (315/sqrt(99810))j + (24/sqrt(99810))k

Now we can compute the dot product u · v:

u · v = (3)(3/sqrt(99810)) + (-315)(-315/sqrt(99810)) + (24)(24/sqrt(99810))

= 9/ sqrt(99810) + 99225/ sqrt(99810) + 576/ sqrt(99810)

= 997.723/ sqrt(99810)

Therefore, u · v is approximately 31.62.

Learn more about vector

https://brainly.com/question/29740341

#SPJ4

Constant of variation = number of chairs/ spacing.

80/16 = 5

The answer is B.5

Answer:

A

Step-by-step explanation:

Karma can buy 1000 shares of T-Bank.

When something is "invested," money or other resources are used with the intention of making a profit, creating income, or appreciating in value over time.

The price of a share at a 25% premium is calculated as follows:

100 + (25/100) * 100 = 125.

Thus, Karma can purchase the following items for Nu 125,000:

125000 / 125 = 1000

So, Karma can buy 1000 shares of T-Bank.

Learn more about investments here : brainly.com/question/25300925

#SPJ1

Range is R={n^2: n is natural number} U {n(n+1) : n is natural number}

The expression ⌈y⌉⋅⌊y⌋ represents the product of the ceiling and floor functions of y.

To find the range of all possible values of y, we need to consider the possible values of the ceiling and floor functions individually.

1. Ceiling function (⌈y⌉): This function rounds y up to the nearest integer. Since y is greater than 0, the ceiling of y will always be greater than or equal to y.

2. Floor function (⌊y⌋): This function rounds y down to the nearest integer. Again, since y is greater than 0, the floor of y will always be less than or equal to y.

Now, let's consider the product of the ceiling and floor functions, ⌈y⌉⋅⌊y⌋.

The product ⌈y⌉⋅⌊y⌋ will always be greater than or equal to 0 since y > 0 and this can take only integral values.

Therefore, the range of all possible values of y such that ⌈y⌉⋅⌊y⌋ is the set R={n^2: n is natural number} U {n(n+1): n is natural number}

Learn more about Floor Function: https://brainly.com/question/24306698

#SPJ11

Note: You seem to have missed entering the complete question. I am assuming you want to get the simplified version of the stated expression. So, I will solve it accordingly.

Answer:

The simplification of the expression is:

\(3\left(4h+2k\right)\cdot \:3=\:36h+18k\)

Step-by-step explanation:

Given the expression

\(3\left(4h+2k\right)3\)

simplifying the expression

\(3\left(4h+2k\right)3\)

\(=3\left(4h+2k\right)\cdot \:3\)

\(=3\cdot \:3\left(4h+2k\right)\)

\(\mathrm{Apply\:the\:distributive\:law}:\quad \:a\left(b+c\right)=ab+ac\)

\(=3\cdot \:3\cdot \:4h+3\cdot \:3\cdot \:2k\)

\(\mathrm{Multiply\:the\:numbers:}\:3\cdot \:3\cdot \:4=36\)

\(=36h+3\cdot \:3\cdot \:2k\)

\(\mathrm{Multiply\:the\:numbers:}\:3\cdot \:3\cdot \:2=18\)

\(=36h+18k\)

Therefore, the simplification of the expression is:

\(3\left(4h+2k\right)\cdot \:3=\:36h+18k\)

Answer:

a

Step-by-step explanation:

Answer:

She used 1/8 or 12.5% more flour than sugar

Step-by-step explanation:

flour: 5/8

sugar: 1/2 = 4/8

\(\frac{5}{8} - \frac{4}{8} = \frac{1} {8} = 0.125\)

0.125 = 12.5%

Answer:

x = 7

Step-by-step explanation:

Given

y = 5x - 3 ← equate 5x - 3 to 32

5x - 3 = 32 ( add 3 to both sides )

5x = 35 ( divide both sides by 5 )

x = 7 ← input

Answer:

x=7

Step-by-step explanation:

y=5x-3

y = 32

32 = 5x- 3

Add 3 to each side

32+3 = 5x-3+3

35 = 5x

Divide by 5

35/5 = 5x/5

7 =x

Answer: 11,244,000

Step-by-step explanation:

From the question, we are informed that In 2013 the population of New York state was approximately 19.65 million and the population of New York City was 8,406,000.

To know the number of people in New York State did not live in New York City, we subtract 8,406,000 from 19.65 million. This will be:

= 19,650,000 - 8,406,000

= 11,244,000

Step-by-step explanation:

3 stands in 300

Transformation involves changing the position of a function.

The path of the ball from y = x^2 is obtained by

The function is given as:

\(\mathbf{y=-16x^2+32x+3}\)

Factor out -16

\(\mathbf{y=-16(x^2-2x)+3}\)

-------------------------------------------------------------------------------

Take the coefficient of x

\(\mathbf{k = -2}\)

Divide by 2

\(\mathbf{k/2 = -1}\)

Take it square

\(\mathbf{(k/2)^2 = 1}\)

-------------------------------------------------------------------------------

Add and subtract the 1 in the bracket of \(\mathbf{y=-16(x^2-2x)+3}\)

\(\mathbf{y=-16(x^2-2x+ 1 - 1)+3}\)

Open bracket

\(\mathbf{y=-16(x^2-2x+ 1) + 16+3}\)

\(\mathbf{y=-16(x^2-2x+ 1) + 19}\)

Express as squares

\(\mathbf{y=-16(x- 1)^2 + 19}\)

The above means that:

Read more about transformation at:

https://brainly.com/question/11709244

If you were able to add the numbers 26 and 41 in your head, it is assumed that you would be doing this in your working memory.

A cognitive apparatus known as working memory has a finite capacity and can only temporarily store information. It is crucial for reasoning, decision-making, and behaviour direction. When working on a long-division problem, kids use their working memory abilities to retain the long-division steps. Other instances include keeping track of complicated instructions, taking notes in class, recalling an argument while someone else is speaking, or performing mental calculations. In contrast to long-term memory, which stores a large amount of knowledge over a lifetime, working memory is the little amount of information that may be kept in mind and used to carry out cognitive tasks. One of the most often used concepts in psychology is working memory.

Given,

If you were able to add the numbers 26 and 41 in your head, it is assumed that you would be doing this in your:

d) Working memory

To learn more about working memory, visit:

https://brainly.com/question/6292992

#SPJ4

Given:

Eighteen 2.5 gallon buckets are needed to fill a cistern with water.

To find:

The constant of variation.

Solution:

If y is directly proportional to x, then

\(y\propto x\)

\(y=kx\)

Where, k is constant of variation.

In the given problem, water in cistern (w) is directly proportional to number of buckets (n).

\(w\propto n\)

\(w=2.5n\)        (Capacity of each bucket is 2.5 gallons)

Therefore, the constant of variation is 2.5.

Answer:

45

Step-by-step

I just did 18 * 2.5!

It a simple answer!

The quantites are inversely so that means you multiply the numbers. Like 18 * 2.5. That's how I got 45

Answer:

y = - \(\frac{1}{3}\) x + \(\frac{5}{3}\)

Step-by-step explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

here m = - \(\frac{1}{3}\) and c = \(\frac{5}{3}\) , then

y = - \(\frac{1}{3}\) x + \(\frac{5}{3}\) ← equation of line

The value of x would be 1496 m.

What is trigonometry?

Trigonometry is based on the study of the six basic trigonometric functions: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). These functions are defined in terms of the ratios of the sides of a right triangle. For example, the sine of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.

In the given figure, we can apply the trigonometric ratio, we get

sin22 = x/4000

0.374 = x/ 4000

x = 0.374 * 4000

x = 1496m

Hence, the value of x would be 1496 m.

To learn more about trigonometry, visit:

https://brainly.com/question/24349828

#SPJ1