multiplicative inverse of 3/7 x 2/7
Answers
Sorry if I didn't understand the question right-
Answer:
\(\frac{49}{6}\)
Step-by-step explanation:
The inverse of \(\frac{3}{7}\) is \(\frac{7}{3}\).
The inverse of \(\frac{2}{7}\) is \(\frac{7}{2}\).
Now we multiply:
\(\frac{7}{3}\) × \(\frac{7}{2}\) = \(\frac{49}{6}\)
Hope this helped :)
Related Questions
1.
I Which number line shows the solution to the inequality
-3x - 5 < -2?
A.
B.
C.
D.
-3 -2 -1 0 1
-3 -2 -1 0 1
0++
0 1
3 -2 -1 0
2 3
2 3
2 3
+++
-3 -2 -1 0 1 2 3
Answers
which methods correctly solve for the variable s in the equation -2 - 5s =9?

Answers
Solve the quadratic equation for x. What is one of the roots?
3x2 − 14x − 5 = 0
please any help would be nice!!!
Answers
The roots of the quadratic equation \(3x^2 - 14x - 5 = 0\), in exact square root form, are x = 5 and x = -1/3.
According to given information :Using the quadratic formula to solve the quadratic equation \(3x^2 - 14x - 5 = 0\),we have
\(x = (-(-14) ± sqrt((-14)^2 - 4(3)(-5))) / (2(3))\\x = (14 ± sqrt(14^2 + 4(3)(5))) / (2(3))\\x = (14 ± sqrt(196 + 60)) / 6\\x = (14 ± sqrt(256)) / 6\\x = (14 ± 16) / 6\\\)
Therefore, the two roots of the quadratic equation in exact square root form are:
\(x = (14 + 16) / 6 = 5\\x = (14 - 16) / 6 = -1/3\\\)
Thus, the roots of the quadratic equation \(3x^2 - 14x - 5 = 0\), in exact square root form, are x = 5 and x = -1/3.
What is quadratic equation ?A quadratic equation is a second-degree polynomial equation in one variable of the form:
\(ax^2 + bx + c = 0\)
where x is the variable, and a, b, and c are constants. In this equation, the highest power of x is 2, and it is called the coefficient of x^2. The coefficient of x is b, and the constant term is c.
The quadratic equation is called "quadratic" because the highest power of x is a square (i.e., x^2), and the graph of the equation is a parabola.
The quadratic equation can have zero, one, or two real solutions, depending on the values of a, b, and c. The solutions can be found by using the quadratic formula:
\(x = (-b ± √(b^2 - 4ac)) / 2a\)
where the symbol ± means "plus or minus" and the square root is of the discriminant (b^2 - 4ac).
To know about quadratic equation visit:
https://brainly.com/question/1526946
#SPJ1
100 Points! Algebra question. Write a quadratic equation in standard form with -1/2, 3/4 as its roots. Please show as much work as possible. Photo attached. Thank you!

Answers
X^2 -(a+b)x + ab = 0
x^2 -(-1/2 + 3/4)x + (-1)(3)/(2)(4) =0
x^2 -(1/4)x -(3/8) = 0
Help fast please, AC= ?

Answers
pls help i dont get it much
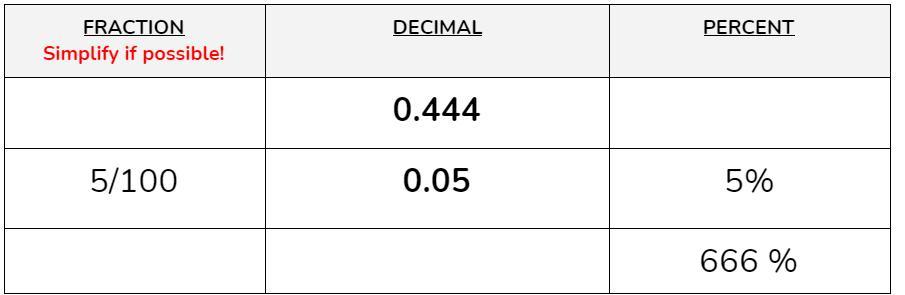
Answers
Answer:
Fraction Decimal Percent
111/250 = 0.444 = 44.4%
5/100 = 0.05 = 5%
2/3 = 0.66 = 666%
I need help with this question

Answers
Using word problems and equations, Sarah worked for 10 hours and Penelope worked for 5 hours
What is the number of hours Sarah and Penelope worked?This is a word problem and in order to solve this, we need to translate mathematical statements in form of word problems into mathematical equations.
Let's assume that Sarah worked x hours.
Given that Sarah can iron 30 shirts per hour, the total number of shirts she ironed is 30x.
Since Penelope worked half the hours of Sarah, Penelope worked x/2 hours.
Given that Penelope can iron 35 shirts per hour, the total number of shirts she ironed is 35 * (x/2) = (35/2)x.
The total number of shirts ironed by both Sarah and Penelope is 475 shirts.
So, we can write the equation: 30x + (35/2)x = 475.
To solve this equation, we can simplify it: (60/2)x + (35/2)x = 475, which becomes (95/2)x = 475.
Now, we can solve for x: x = (475 * 2) / 95 = 10.
Therefore, Sarah worked 10 hours and Penelope worked half of that, which is 5 hours.
learn more on word problems here;
https://brainly.com/question/13818690
#SPJ1
Never mind i got it!
Answers
Answer:
OOk
Step-by-step explanation:
The perimeter of a trianglular pool is 36
yards the length of two sides or 10 yards and 15 yards how long is the third side
Answers
Answer:
11 yard
Step-by-step explanation:
Let the 3rd side be 'a'.
Perimeter = 36
=> sum of sides = 36
=> 10 + 15 + a = 36
=> 25 + a = 36
=> a = 36 - 25
=> a = 11
Express the integrand as a sum of partial fractions and evaluate the integral.
\int \frac {2x^{3}+5x^{2}+ 14x+7}{(x^{2}+2x+5)^{2}} dx

Answers
By simplifying quadratic equation we get the integral as \(-\sqrt{x^2 + 2x + 5}/2 + 7ln|x^2 + 2x + 5|/2 + (x^2 - 10)/(50(x^2 + 2x + 5)) + C\)
What is quadratic equation ?
A quadratic equation is a second-degree polynomial equation of the form \(ax^2 + bx + c = 0\), where x is an unknown variable, and a, b, and c are constants, and a ≠ 0. The name comes from the Latin word "quadratus," which means "square." The highest power of x is 2, which means it is a quadratic equation. Quadratic equations can have one, two, or zero real solutions, depending on the values of a, b, and c. They have important applications in many fields, including physics, engineering, and finance.
According to the question:
We start by factoring the denominator using the quadratic formula:
\(x^2 + 2x + 5 = 0\)
\(x = (-2 ± \sqrt{4 - 4(1)(5))} / 2\)
\(x = -1 \± 2i\)
So the denominator factors as:
\(x^2 + 2x + 5 = (x - (-1 + 2i))(x - (-1 - 2i))\)
Now we can express the integrand as a sum of partial fractions:
\(\frac {2x^{3}+5x^{2}+ 14x+7}{(x^{2}+2x+5)^{2}} = \frac{Ax + B}{x^2 + 2x + 5} + \frac{Cx + D}{(x^2 + 2x + 5)^2}\)
Multiplying both sides by the common denominator, we have:
\(2x^3 + 5x^2 + 14x + 7 = (Ax + B)(x^2 + 2x + 5) + (Cx + D)\)
Expanding and equating coefficients, we get the following system of equations:
A + C = 0
B + 2A - C + D = 2
5A + 2B + D = 0
10A + 5B + 2C = 14
25B = 7
Solving for A, B, C, and D, we find:
A = -1/25
B = 7/25
C = 1/25
D = -2/25
Therefore, the integrand can be written as:
\(\frac {2x^{3}+5x^{2}+ 14x+7}{(x^{2}+2x+5)^{2}} = \frac{-x/25 + 7/25}{x^2 + 2x + 5} + \frac{x/25 - 2/25}{(x^2 + 2x + 5)^2}\)
To evaluate the integral, we can use the substitution \(u = x^2 + 2x + 5\). Then du/dx = 2x + 2, so dx = du/(2x + 2). Substituting into the integral, we get:
\(\int\frac {2x^{3}+5x^{2}+ 14x+7}{(x^{2}+2x+5)^{2}} dx = \int\frac{-u^{-1/2} + 7u^{-1}}{2} du + \int\frac{(u-10)u^{-2}}{25} du\)
Simplifying and integrating, we get:
\(\int\frac {2x^{3}+5x^{2}+ 14x+7}{(x^{2}+2x+5)^{2}} dx = -\sqrt{x^2 + 2x + 5}/2 + 7ln|x^2 + 2x + 5|/2 + (x^2 - 10)/(50(x^2 + 2x + 5)) + C\)
where C is the constant of integration.
To know more about quadratic equation visit:
https://brainly.com/question/30098550
#SPJ1
Hi can anyone help me with this much appreciate j

Answers
For the given arena's tickets sales , the round of figure of all the sales to the nearest thousand is given by :
Events Nearest thousand
Dart Domination cup : $169,000Boadicea's basketball league : $40,000The Rub-a-Dub Club Reggae band : $215,000Agent Green : $65,000Britney Pitchfork : $224,000Sunshine Droops : $111,000
As given in the question,
Rules to round of nearest thousand are:
Check the near by hundred digit :
If the hundred digit is 5 or more than 5 than round up that is write next digit. If the hundred digit is less than 5 than round down.Given is the actual ticket rates of the different events tickets sales ,round off to the nearest thousand is given by:
Events Nearest thousand
Dart Domination cup : $169,000Boadicea's basketball league : $40,000The Rub-a-Dub Club Reggae band : $215,000Agent Green : $65,000Britney Pitchfork : $224,000Sunshine Droops : $111,000
Therefore, For the given arena's tickets sales , the round of figure of all the sales to the nearest thousand is given by :
Events Nearest thousand
Dart Domination cup : $169,000Boadicea's basketball league : $40,000The Rub-a-Dub Club Reggae band : $215,000Agent Green : $65,000Britney Pitchfork : $224,000Sunshine Droops : $111,000
Learn more about nearest thousand here
brainly.com/question/113800
#SPJ1
The University of Arkansas recently reported that 43% of college students aged 18-24 would spend their spring break relaxing at home. A sample of 165 college students is selected.
a. Calculate the appropriate standard error calculation for the data.
b. What is probability that more than 50% of the college students from the sample spent their spring breaks relaxing at home?
Answers
Answer:
a. 0.0385
b. 3.44% probability that more than 50% of the college students from the sample spent their spring breaks relaxing at home
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
In this question:
\(p = 0.43, n = 165\)
a. Calculate the appropriate standard error calculation for the data.
\(s = \sqrt{\frac{0.43*0.57}{165}} = 0.0385\)
b. What is probability that more than 50% of the college students from the sample spent their spring breaks relaxing at home?
This is 1 subtracted by the pvalue of Z when X = 0.5. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.5 - 0.43}{0.0385}\)
\(Z = 1.82\)
\(Z = 1.82\) has a pvalue of 0.9656
1 - 0.9656 = 0.0344
3.44% probability that more than 50% of the college students from the sample spent their spring breaks relaxing at home
Find the unit rate (constant of proportionality) of the distance traveled.
Number of hours
0.25 1.5 2.5 3
Distance traveled (km) 3 18 30 36
Answers
Answer:
12.
Step-by-step explanation:
if to re-write the given condition, then
\(\frac{3}{0.25} =\frac{18}{1.5} =\frac{30}{2.5} =\frac{36}{3} ;\)
it is clear, the required constant is 12 (12 per hour).
Q2. Evaluate: (a) \( j^{12} \); (b) \( -\frac{1}{j^{9}} \); (c) \( \frac{5}{2 j^{13}} \)
Answers
the evaluated expressions are: (a) j¹² = 1 ,(b) -1/j⁹ = j ,(c) 5/(2j¹³) = (5/2)j
to solve this use the properties of the imaginary unit.
what is imaginary unit ?
The imaginary unit is a mathematical concept denoted by i or j (in electrical engineering) that represents the square root of -1. It is called an "imaginary" unit because it does not have a real number counterpart.
In the given question,
To evaluate these expressions, we need to recall the properties of the imaginary unit, j, which is defined as the square root of -1. Specifically, we need to remember that:
j² = -1
j³ = -j
j⁴ = 1
Using these properties, we can simplify the given expressions:
(a) j¹² = (j⁴)³ = 1³ = 1
(b) -1/j⁹ = -1/(j³)³= -1/(-j)³ = -1/(-j³) = -1/(-(-j)) = -1/j = -j/j² = -j/-1 = j
(c) 5/(2j¹³) = 5/(2(j⁴)³*j) = 5/(2*1*j) = 5/(2j) = (5/2) * (1/j) = (5/2) * (-j³/j⁴) = -(5/2)j³ = (5/2)j
Therefore, the evaluated expressions are:
(a) j¹² = 1
(b) -1/j⁹ = j
(c) 5/(2j¹³) = (5/2)j
To know more about imaginary unit , visit:
https://brainly.com/question/29274771?referrer=searchResults
#SPJ1
. Evaluate the following expression to simplest form \( j^{12} \); (b) \( -\frac{1}{j^{9}} \); (c) \( \frac{5}{2 j^{13}} \)
What is the color blue
Answers
Answer:
Blue is one of the three primary colours of pigments in painting and traditional colour theory, as well as in the RGB colour model. It lies between violet and green on the spectrum of visible light. The eye perceives blue when observing light with a dominant wavelength between approximately 450 and 495 nanometres
Step-by-step explanation:
what do I say
SASAGEYO
Louren measures the distance around her circular mirror to
be 166.5 centimeters. She plans to put lace across the
center of the mirror.
Approximately how many inches of lace does she needs
Answers
Answer:
53 cm.
Step-by-step explanation:
Circumference = pi times diameter
We are trying to find diameter so rearrange
Circumference/pi = diameter
166.5/pi = 52.998596
Approximately 53 centimeters of lace
PLEASE HELP DUE TODAY

Answers
9514 1404 393
Answer:
16 square units
Step-by-step explanation:
When you plot the points, you see they define a trapezoid with bases of lengths 2 and 6, and a height of 4. The area formula is ...
A = (1/2)(b1 +b2)h
A = (1/2)(2 +6)(4) = 16
The area of the trapezoid is 16 square units.

Find the value of x
Write ur answer in simplest form

Answers
Step-by-step explanation:
a^2+b^2=c^2
x^2+x^2= (3√2)^2
2x^2=9×2
x^2=9
x=3
What is sin30? What is cos30? What is tan60?

Answers
Answers:
\(\sin(30^{\circ}) = \frac{1}{2}\\\\\\\cos(30^{\circ}) = \frac{\sqrt{3}}{2}\\\\\\\tan(60^{\circ}) = \sqrt{3}\\\\\)
=======================================================
Work Shown:
Problem 1
\(\sin(\text{angle}) = \frac{\text{opposite}}{\text{hypotenuse}}\\\\\sin(30^{\circ}) = \frac{7}{14}\\\\\sin(30^{\circ}) = \frac{1}{2}\\\\\)
-------------------------
Problem 2
\(\cos(\text{angle}) = \frac{\text{adjacent}}{\text{hypotenuse}}\\\\\cos(30^{\circ}) = \frac{7\sqrt{3}}{14}\\\\\cos(30^{\circ}) = \frac{\sqrt{3}}{2}\\\\\)
------------------------
Problem 3
\(\tan(\text{angle}) = \frac{\text{opposite}}{\text{adjacent}}\\\\\tan(60^{\circ}) = \frac{7\sqrt{3}}{7}\\\\\tan(60^{\circ}) = \sqrt{3}\\\\\)
What is the area of the square that measures 3.1 m on each side
Answers
The area of the square with a side length of 3.1 meters is 9.61 square meters.
To find the area of a square, we need to multiply the length of one side by itself. In this case, the square has a side length of 3.1 m.
Area of a square = side length × side length
Substituting the given side length into the formula:
Area = 3.1 m × 3.1 m
To perform the calculation:
Area = 9.61 m²
It's worth noting that when calculating the area, we are working with squared units. In this case, the side length is in meters, so the area is expressed in square meters (m²). The area represents the amount of space enclosed within the square.
Remember, to find the area of any square, you simply need to multiply the length of one side by itself.
The area of the square with a side length of 3.1 meters is 9.61 square meters.
For more such questions on square
https://brainly.com/question/27307830
#SPJ8
Dwayne estimated his mass as
6 kilograms. Is his estimate reasonable? Explain your answer.
Answers
Answer:
no this is only about 13 pounds
Step-by-step explanation:
Answer:
no
Step-by-step explanation:
it's not reasonable
I don't need lengthy details I just want the answer

Answers
Answer:
Sue rode 1885 miles total
Step-by-step explanation:
There are 31 days in March, 30 in April, and 30 in May.
31 * 12 + 30 * 12 + 30 * 12 = 1092
There are 30 days in June and 31 in august.
30 * 13 + 31 * 13 = 793
Now we find the total:
1092 + 793 = 1885
A triangle is shown with its exterior angles. The interior angles of the triangle are angles 2, 3, 5. The exterior angle at angle 2 is angle 1. The exterior angle at angle 3 is angle 4. The exterior angle at angle 5 is angle 6. Which statements are always true regarding the diagram? Select three options. m∠5 + m∠3 = m∠4 m∠3 + m∠4 + m∠5 = 180° m∠5 + m∠6 =180° m∠2 + m∠3 = m∠6 m∠2 + m∠3 + m∠5 = 180°
Answers
A triangle is shown with its exterior angles and the interior angles of the triangle are angles 2, 3, 5. The true statements are m∠3 + m∠4 + m∠5 = 180°, m∠5 + m∠6 = 180°, and m∠2 + m∠3 = m∠6. The correct answers are B, C, and E.
We know that the sum of the measures of the interior angles of a triangle is always 180 degrees. We can use this fact, along with the properties of exterior angles of a triangle, to determine which statements are always true regarding
m∠5 + m∠3 = m∠4 This statement is not always true. It is only true in this case because angle 4 is an exterior angle at vertex 3, which means that m∠4 = m∠3 + m∠5. Therefore, m∠5 + m∠3 = m∠3 + m∠5, which simplifies to m∠5 = m∠5. However, in general, this statement is not always true.
m∠3 + m∠4 + m∠5 = 180° This statement is always true, because the sum of the measures of the three exterior angles of a triangle is always 360 degrees. Therefore, m∠3 + m∠4 + m∠5 = 360°, which simplifies to m∠3 + m∠4 + m∠5 = 180°.
m∠5 + m∠6 = 180° This statement is always true, because the sum of an exterior angle and its adjacent interior angle is always 180 degrees. Therefore, m∠5 + m∠6 = m∠1 (because angle 1 is an exterior angle at vertex 2), and m∠1 + m∠2 + m∠3 = 180° (because the sum of the measures of the interior angles of a triangle is 180 degrees). Therefore, m∠5 + m∠6 = m∠2 + m∠3, which is equal to 180° (because m∠2 + m∠3 = m∠1, and m∠5 + m∠6 = m∠1).
m∠2 + m∠3 = m∠6 This statement is not always true. It is only true in this case because angle 6 is an exterior angle at vertex 5, which means that m∠6 = m∠5 + m∠3. Therefore, m∠2 + m∠3 = m∠2 + m∠5 + m∠3, which simplifies to m∠2 + m∠3 = m∠5 + m∠3. Then, by subtracting m∠3 from both sides, we get m∠2 = m∠5. However, in general, this statement is not always true.
m∠2 + m∠3 + m∠5 = 180°: This statement is always true, because the sum of the measures of the interior angles of a triangle is always 180 degrees. Therefore, m∠2 + m∠3 + m∠5 = 180°.
Based on the above analysis, the statements that are always true regarding the diagram are
m∠3 + m∠4 + m∠5 = 180°
m∠5 + m∠6 = 180°
m∠2 + m∠3 + m∠5 = 180°
Therefore, the correct options are B, C, and E.
To know more about triangle:
https://brainly.com/question/28835566
#SPJ1

If a three-digit number is divided by 5 or by 6, remainder is 1 in each case. What is the least such three-digit number?
Answers
Answer:
The least three-digit number which leaves a remainder of 1 when divided by 5 or 6 is 101.
Step-by-step explanation:
This is because 101 is the smallest three-digit number which is not a multiple of either 5 or 6. To see that 101 is the smallest such number, you can check that 100 and 99 are both multiples of both 5 and 6, and 98 is a multiple of 6.
The side of a triangle are in the ratio 4:4:3 what kind of triangle is it (b) calculate the smallest angle of the triangle to the nearest degree
Answers
The smallest angle of the equilateral triangle is 60 degrees
If the sides of a triangle are in the ratio 4:4:3, it implies that the lengths of the sides are proportional.
To determine the type of triangle, we examine the side lengths. Since all three sides are equal in length, we have an equilateral triangle.
For an equilateral triangle, all angles are equal. To calculate the smallest angle, we divide the total sum of angles in a triangle (180 degrees) by the number of angles, which is 3:
Smallest angle \(= \frac{180}{3} = 60\)\) degrees.
Therefore, the smallest angle of the equilateral triangle is 60 degrees (to the nearest degree).
For more questions on equilateral triangle:
https://brainly.com/question/17264112
#SPJ8
2 Mabaso has R140, Thabo has R70 and Ally has R35. What is the ratio of the amount of money Mabaso has, to the amount of money Thabo has and to the amount of money Ally has? Write the ratios in simplest form. The price of a steel table is R750. On Black Friday the table could be bought for R600. Calculate the percentage discount? Show ALL your calculations. Convert 125 g to kilograms. (1 kg = 1 000 grams) A green grocer packs 12 apples in a plastic bag. Calculate the number of bags he w need if he has 285 apples. The scale of a map is 1 500 000. Determine the actual distance in km if measurement on the map is 23,7 cm. Hint: 1 km = 100 000 cm
Answers
The actual distance represented by 23.7 cm on the map is 355.5 km.
To find the ratio of the amount of money Mabaso has to the amount of money Thabo has and the amount of money Ally has, we can divide each amount by the smallest amount (which is R35) to simplify the ratio.
Mabaso has R140, Thabo has R70, and Ally has R35.
The ratio of Mabaso's money to Thabo's money is:
R140 ÷ R35 = 4
The ratio of Mabaso's money to Ally's money is:
R140 ÷ R35 = 4
Therefore, the ratio of the amount of money Mabaso has to the amount of money Thabo has and to the amount of money Ally has is 4:1:1.
To calculate the percentage discount of a steel table, we need to find the difference between the original price and the discounted price, and then divide it by the original price. Finally, we multiply the result by 100 to get the percentage.
Original price: R750
Discounted price: R600
Discount: R750 - R600 = R150
Percentage discount: (R150 ÷ R750) × 100 = 20%
So, the table has a 20% discount on Black Friday.
To convert 125 grams to kilograms, we divide the amount in grams by 1,000 (since there are 1,000 grams in a kilogram).
125 g ÷ 1,000 = 0.125 kg
Therefore, 125 grams is equal to 0.125 kilograms.
If a green grocer packs 12 apples in a plastic bag and has 285 apples, we divide the total number of apples by the number of apples per bag to determine the number of bags needed.
Number of bags needed: 285 apples ÷ 12 apples/bag = 23.75 bags
Since we can't have a fraction of a bag, we round up to the nearest whole number. Therefore, the green grocer would need 24 bags.
If the scale of a map is 1,500,000 and the measurement on the map is 23.7 cm, we can use the scale to determine the actual distance.
1 cm on the map represents 1,500,000 cm in reality.
23.7 cm on the map represents x cm in reality.
x = 23.7 cm × 1,500,000 cm = 35,550,000 cm
To convert cm to km, we divide by 100,000 (since there are 100,000 cm in a kilometer).
35,550,000 cm ÷ 100,000 = 355.5 km
For more such questions on distance
https://brainly.com/question/30395212
#SPJ8
Multiply: 3,217 × 5,716
Answers
Answer:
Step-by-step explanation:
183,883,72
Answer:
18388372
Step-by-step explanation:
1 )Use the algorithm method.
3 2 1 7
× 5 7 1 6
1 1 1 4
1 9 3 0 2
3 2 1 7 0
2 1 1 4
2 2 5 1 9 0 0
1 1 3
1 6 0 8 5 0 0 0
1 1 1
1 8 3 8 8 3 7 2
==================step 2==================2 )Therefore, 3217 × 5716 = 18388372.
18388372
Find the measurements of the missing side. Be sure to simplify your answer.

Answers
Answer:
the answer is 13 for this problem
Answer:
13
Step-by-step explanation:
\({a}^{2} + {b}^{2} = {c}^{2} \)
\( {5}^{2} + {12}^{2} = {c}^{2} \)
\( {c}^{2} = 169\)
\(c = \sqrt{169} \)
\(c = 13\)
Tony left the party early traveling 2 mph. 15 hours later, Pamela decided to head out and catch up with him. She ran 7 mph. How long would she have to run to catch up with him?
Answers
Pamela would have to run approximately 4.29 hours to catch up with Tony.
To determine how long Pamela would have to run to catch up with Tony, we need to find the time it takes for Pamela to cover the distance Tony covered during the 15 hours he had already been traveling.
Since Tony traveled at a constant speed of 2 mph for 15 hours, the distance he covered is given by:
Distance = Speed * Time
Distance = 2 mph * 15 hours
Distance = 30 miles
Now, Pamela wants to catch up with Tony, so she needs to cover the same distance of 30 miles. Pamela runs at a speed of 7 mph.
To find the time it takes for Pamela to cover the distance of 30 miles, we can use the formula:
Time = Distance / Speed
Time = 30 miles / 7 mph
Using division, we find:
Time ≈ 4.29 hours
Therefore, Pamela would have to run approximately 4.29 hours to catch up with Tony.
For more questions on hours
https://brainly.com/question/28815991
#SPJ8
A survey of 400 students yielded the following information: 262 were seniors, 215 were commuters, and 150 of the seniors were commuters. How many of the 400 surveyed students were seniors or were commuters?
Answers
Out of the 400 surveyed students, 327 were either seniors or commuters.
To find the number of students who were either seniors or commuters out of the 400 surveyed students, we need to add the number of seniors and the number of commuters while avoiding double-counting those who fall into both categories.
According to the information given:
There were 262 seniors.
There were 215 commuters.
150 of the seniors were also commuters.
To avoid double-counting, we need to subtract the number of seniors who were also commuters from the total count of seniors and commuters.
Seniors or commuters = Total seniors + Total commuters - Seniors who are also commuters
= 262 + 215 - 150
= 327
Therefore, out of the 400 surveyed students, 327 were either seniors or commuters.
It's important to note that in this calculation, we accounted for the overlap between seniors and commuters (150 students who were both seniors and commuters) to avoid counting them twice.
This ensures an accurate count of the students who fall into either category.
For similar question on surveyed.
https://brainly.com/question/14610641
#SPJ8