Mr. Martin runs 7 miles per hour. How far will
he have run if he runs for 3 hours?
Answers
Answer:
He would have run 21 miles in 3 hours.
Step-by-step explanation:
Related Questions
help me answer question 8a and b, and I’ll give u 10 points lol

Answers
Answer:
Step-by-step explanation:
Find h when v = 20 and r = 3
Putting values in the formula
20 = (3.14)(3)2h
20 = (3.14)(9)h
20 = 28.26h
20/28.26 = h
R when v = 100 and h = 5
100 = (3.14)r2(5)
100/5 = 3.14r2
20 = 3.14r2
20/3.14 = r2
6.36 = r2
Square root on both sides
2.52 = r
Find the Principal unit normal for r(t) = sintit cost; + tk Evaluate it at t = Tyz Sketch the situation
Answers
We can plot the vector r(t) and the vector N(T) at the given value of t = T.
To find the principal unit normal for the vector-valued function r(t) = sin(t)i + tcos(t)j + tk, we need to compute the derivative of r(t) with respect to t and then normalize it to obtain a unit vector.
First, let's find the derivative of r(t):
r'(t) = cos(t)i + (cos(t) - tsin(t))j + k
Next, we'll normalize the vector r'(t) to obtain the unit vector:
||r'(t)|| = sqrt((cos(t))^2 + (cos(t) - tsin(t))^2 + 1^2)
Now, we can find the principal unit normal vector by dividing r'(t) by its magnitude:
N(t) = r'(t) / ||r'(t)||
Let's evaluate the principal unit normal at t = T:
N(T) = (cos(T)i + (cos(T) - Tsin(T))j + k) / ||r'(T)||
To sketch the situation, we can plot the vector r(t) and the vector N(T) at the given value of t = T.
Learn more about vector from
https://brainly.com/question/28028700
#SPJ11
please help (attachment shown below) for 50 pointz hurry

Answers
Answer:
I got C
Step-by-step explanation:
Answer:
2021
Step-by-step explanation:
Point s is located at (4,-3) if point s is reflected over the x axis, what will be the new location of point s
Answers
The point (x,y) on reflection over x-axis, chanes to (x,-y) or x-xoordinate remain same and y-coordinate changes.
So point (4,-3) after reflection over the x-axis changes to (4,3).
Answer: (4,3)
Determine the equation of the circle with center (-3, -8) containing the point (-11, -23).
Answers
The equation of the circle with center (-3, -8) containing the point (-11, -23) is x²+y²+6x+16y=216.
The general form of the equation of the circle is (x-h) ²+(y-k) ²=r².
Here, (h, k) indicates the circle's center, and r indicates the circle's radius.
In the given question, (-3, -8) is the center of the circle.
Here, h = -3, k = -8.
Now, we need to find the radius of the circle.
Radius is the distance between the center of the circle and the given point (-11, -23).
Distance formula = √(x2-x1) ²+(y2-y1) ²
√ (-11-(-3)) ² + (-23-(-8)) ²
√ (-11+3) ² + (-23+8) ²
√64+225
√289
17.
So, the radius of the circle is 17.
Now, we can find the equation of the circle by substituting in the formula.
(x-h) ² + (y-k) ² = r²
(x-(-3)) ² + (y - (-8)) ² = 17²
(x+3) ² + (y+8) ² = 289.
x²+6x+9+y²+16y+64=289
x²+y²+6x+16y=216.
Therefore, the equation of the circle is x²+y²+6x+16y=216.
To know more about the Equation of Circle, click on: https://brainly.com/question/29288238.
.2. Determine whether the feasible set for each of the following systems of constraints is convex, and if not, indicate points x^1 and x² that violate definition. a) (x1)² + (x2)² > 9
x1 + x2 ,10
x1, x2 > 0
Answers
The feasible set for this system of constraints is not convex, and the points (5, 5) and (3, 7) violate the convexity definition.
To determine whether the feasible set for each system of constraints is convex, we need to analyze the constraints individually and examine their intersection.
a) (x1)² + (x2)² > 9
This constraint represents points outside the circle with a radius of √9 = 3. The feasible set includes all points outside this circle.
b) x1 + x2 ≤ 10
This constraint represents points that lie on or below the line x1 + x2 = 10. The feasible set includes all points on or below this line.
c) x1, x2 > 0
This constraint represents points in the positive quadrant, where both x1 and x2 are greater than zero.
Now, let's analyze the intersection of these constraints:
Considering the first two constraints (a and b), we can see that the feasible set consists of all points outside the circle (constraint a) and below or on the line x1 + x2 = 10 (constraint b).
To determine whether the feasible set is convex, we need to check if any two points within the set create a line segment that lies entirely within the set.
If we consider the points (5, 5) and (3, 7), both points satisfy the individual constraints (a) and (b). However, the line segment connecting these two points, which is the line segment between (5, 5) and (3, 7), exits the feasible set since it passes through the circle (constraint a) and above the line x1 + x2 = 10 (constraint b).
Therefore, the feasible set for this system of constraints is not convex, and the points (5, 5) and (3, 7) violate the convexity definition.
Learn more about circle here
brainly.com/question/11878555
#SPJ4
A city sewer pipe has a diameter of 6 ft and a length of 100 ft. Find the volume of the pipe use 3.14 as the approximate value of pie. The volume is (simplify your answer. Round to the nearest whole number as needed.)
Answers
We know that the diameter of the pipe is 6 feet.
Given that the pipe is cylindrical, we can use the following formula
\(V=\pi(r)^2h\)Where the radius is half the diameter
\(r=\frac{d}{2}=\frac{6ft}{2}=3ft\)In this case, the height is represented by the length of the pipe
\(h=100ft\)Replacing all these values, we have
\(\begin{gathered} V=3.14(3ft)^2(100ft) \\ V=2,826ft^3 \end{gathered}\)Hence, the volume of the pipe is 2,826 cubic feet, approximately.write the following equation in slope- intercept form 6x+2y=20
Answers
Answer:
y = -3x + 10
Step-by-step explanation:
6x+2y=20
First, you want to subtract 6x from both sides.
2y=-6x+20
Now, you want to divide by 2 on both sides because you want to get y by itself.
y = -3x + 10
Answer:
Y = -3x + 10
Step-by-step explanation:
Subtract the 6x from both sides to get y by itself
You would have 2y=-6x+20
Divide everything by 2 for the correct formula format
You would have y=-3x+10
Write the slope intercept form of the equation of the line that passes through the point (4, 8) and has a slope of -2.
Answers
The equation of the line is y = -2x + 16 which passes through the point (4, 8) and has a slope of -2.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
It is given that:
The line that passes through the point (4, 8) and has a slope of -2.
On comparing the standard equation:
y = mx + c
Here m is the slope of the line and c is the y-intercept.
m = -2
y = -2x + c
Plug x = 4 and y = 8
8 = -2(4) + c
c = 16
y = -2x + 16
Thus, the equation of the line is y = -2x + 16 which passes through the point (4, 8) and has a slope of -2.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ1
someone help me please with this algebra problem
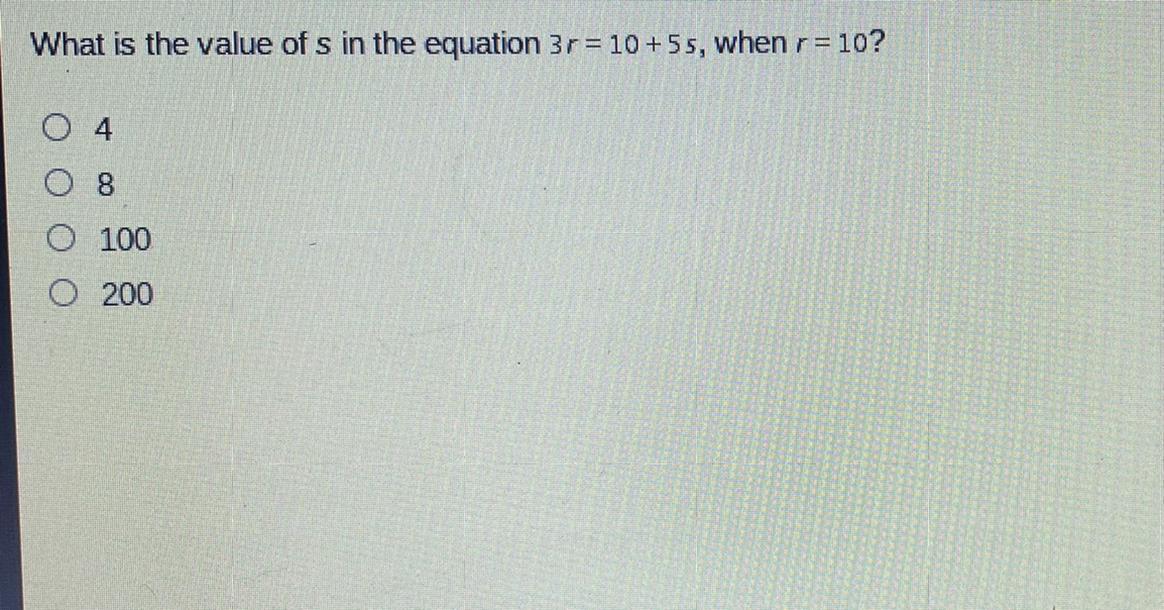
Answers
Answer:
4
Step-by-step explanation:
3r = 10 + 5s
r = 10
3(10) = 10 + 5s
30 = 10 + 5r
20 = 5r
r = 4
What is the point slope form of the line with slope 25 that passes through the point (−4, −7)?
(A) y+7=25(x+4)
(B) y+4=25(x+7)
(C) y−7=25(x−4)
(D) y−4=25(x−7)
Answers
Answer:
Option A: \(y+7 = 25(x+4)\) is the correct answer.
Step-by-step explanation:
The point-slope form of an equation of a line is given by:
\(y-y_1 = m(x-x_1)\)
Here:
m is the slope of the line
\((x_1,y_1)\) are the coordinates of the point from which the line passes.
Now looking at the given question:
\(m = 25\\(x_1,y_1) = (-4,-7)\)
Putting the values in the general form of point-slope form of equation of line
\(y-(-7) = 25\{x-(-4)\}\\y+7 = 25(x+4)\)
Hence, the point-slope form of given line is:
\(y+7 = 25(x+4)\)
Observing the option given, it can be concluded that Option A: \(y+7 = 25(x+4)\) is the correct answer.
There are 1,500 students on campus and 20% of the remaining students leave each day for semester break. How many are remaining after 5 days?
Answers
Which value of x makes the expression above equivalent to 14 Square root 7?
Pls helppppppppppppppp

Answers
Answer:
B. 4
Step-by-step explanation:
First, let's evaluate the first expression:\(7 \sqrt{7x} = \sqrt{49 \times 7x} \)
We can just remove the √ from both sides to make it easier to see, so49 × 7x = 343x
Now, let's evaluate the second expression:14√7 = √(1372)
To see what value would make the first expression equal to the second expression, we can divide the the second expression by first expression:1372 ÷ 343 = 4 this is the vaule of x.
hi i would like sum help :)) please help for a brainlist !!!!!!!!!!!!!

Answers
Explanation:
Domain is the x-values. Since the graph goes forever horizontally, any x-value is on the graph.
Range is the same but with y-values. If the graph went on further than what the picture shows, then it also would show that every y value is on the graph
hope this helps
Stuart bought a sweater on sale for 30% discount off the original price and another 25% off the discounted price . If the original price of the sweater was 600 , what was the final price of a sweater?.
Answers
Answer:
$301.50
Step-by-step explanation:
Given that:
Stuart brought a sweater on sale for 30% discount off.
Another 25% discount off
Original price = 600
To Find:
What was the final price of a sweater?
Solve:
$600 x 30% = $180
$600 - $180 = $402 (discounted price after 30% off)
$402 x 25% = $100.50
$402-100.50 = $301.50 (discounted price after 25% off & the final price)
Hence, the final price is $301.50
Kavinsky
There are 25 prime numbers less than 100.
Some of these are two-digit prime numbers.
What fraction of two-digit prime numbers contain the digit 9?
Express this fraction in lowest terms.
Answers
Answer:
6/25.
Step-by-step explanation:
They are 19, 29, 59, 79, 89 and 97.
A total of 6.
So the required fraction is 6/25.
Two data sets contain an equal number of values. The double box and whisker plot represents the values in the data set. Compare the data sets using measures of center and variation.

Answers
Answer with explanation:
From the box and whisker plot of seventh grade we have:
The minimum value =6
First quartile or lower quartile i.e. = 14
Median or second quartile i.e. = 18
Third quartile or upper quartile i.e. =22
and maximum value = 26
From the box and whisker plot of eighth grade we have:
The minimum value =22
First quartile or lower quartile i.e. = 26
Median or second quartile i.e. = 30
Third quartile or upper quartile i.e. = 34
and maximum value = 38
a)
The overlap of the two sets of data is as follows.
The upper quartile or third quartile of seventh grade is same as the minimum value of the data of eighth grade.
And the maximum value of seventh grade is same as the lower quartile of eighth grade.
b)
IQR is calculated as the difference of the Upper quartile and the lower quartile
i.e.
so, IQR of seventh grade is:
22-14=8
IQR of seventh grade=8
IQR of eighth grade is:
34-26=8
Hence, IQR of eighth grade=8
c)
The difference of the median of the two data sets is:
30-18=12
Hence, the difference of median is: 12
d)
As the IQR of both the sets is same i.e. 8.
Hence, the number that must be multiplied by IQR so that it is equal to the difference between the medians of the two sets is:
Hence, the number is : 1.5
Answer:
ive seen this before
Step-by-step explanation:
help
Lynn is buying her grandson a birthday
present at GameStop. If the game he
wants is regularly $59.99, and all games
are 30% off, how much change will she
get back after paying with a $50 bill?
Answers
Lynn will get approximately $8.01 in change after paying a $50 bill.
To calculate the final price of the game after the 30% discount, we need to subtract 30% of the original price from the original price.
Discounted price = Original price - (Discount percentage * Original price)
Discounted price = $59.99 - (0.30 * $59.99)
Discounted price = $59.99 - $17.997
Discounted price = $41.993 (rounded to the nearest cent)
Now, we can calculate the change Lynn will get back after paying a $50 bill:
Change = Amount paid - Cost of the game
Change = $50 - $41.993
Change = $8.007 (rounded to the nearest cent)
Change = $8.01
More about the percentage link is given below.
https://brainly.com/question/8011401
#SPJ1
the population of a city is expected to be people after years. find the average population between year and year .
Answers
The average population between year 1 and year 10 is approximately 55,555 people.
To find the average population between year X and year Y, we need to first calculate the total population increase over that time period. We can do this by subtracting the population in year X from the population in year Y.
Population increase = Population in year Y - Population in year X
Once we have the population increase, we can divide it by the number of years between X and Y to get the average annual population increase.
Average annual population increase = Population increase / (Y - X)
Finally, to find the average population between year X and year Y, we need to add the average annual population increase to the population in year X.
Average population = Population in year X + Average annual population increase
For example, if the population of a city is expected to be 100,000 people after 10 years, and we want to find the average population between year 1 and year 10, we would do the following:
Population in year 1 = X = 50,000 (let's say)
Population in year 10 = Y = 100,000
Population increase = 100,000 - 50,000 = 50,000
Number of years between X and Y = 10 - 1 = 9
Average annual population increase = 50,000 / 9 = 5,555.56 (rounded)
Average population = 50,000 + 5,555.56 = 55,555.56 (rounded)
Learn more about average here:
https://brainly.com/question/13365551
#SPJ11
The average population of the city between the starting year and 10 years later is estimated to be 625,000.
The average population of a city between two specific years, we will need to use the formula for calculating the arithmetic mean.
The sum of all the values divided by the number of values.
We will need to sum up the populations of the city for each year between the two given years and divide the result by the number of years included.
Let us assume that the population of the city in the year we are starting with is "P1" and the population after "n" years is "P2".
Therefore, the average population can be calculated as:
\(Average Population = (P1 + P2) / 2\)
The exact population figures for each year between the two given years, we will have to use an estimated population growth rate to make the calculation.
We can use the formula:
\(P2 = P1 \times (1 + r)^n\)
where "r" is the estimated annual growth rate and "n" is the number of years between the two given years.
Let's assume that the population of the city in the starting year is 500,000 and the estimated population after 10 years is 750,000. Using the formula, we can calculate the estimated annual growth rate as:
\(r = (P2 / P1)^{(1/n)} - 1 = (750,000 / 500,000)^{(1/10)} - 1 = 0.0473 or 4.73\%\)
The estimated annual growth rate, we can calculate the average population between the two given years using the formula:
\(Average Population = (P1 + P2) / 2 = (500,000 + 750,000) / 2 = 625,000\)
It is important to note that this is just an estimate based on the assumed growth rate, and the actual population may vary from this calculation.
For similar questions on Average Population
https://brainly.com/question/28103278
#SPJ11
Multiply the binomials: (8a - 3b) (3a - 8b)
Answers
Answer:
24a²-73ab+24b²
Step-by-step explanation:
(8a - 3b) (3a - 8b) =
24a²-64ab-9ab+24b²
= 24a²-73ab+24b²
/_AGB and /_EGD are angles

Answers
The angle ∠AGB and ∠EGD are equal angles / opposite angles / vertical angles.
Given,
∠AGB and ∠EGD
We need to find what types of angles are ∠AGB and ∠EGD.
What are vertical angles?Vertical angles are angles that are opposite of each other when two lines cross.
Vertical angles are always equal.
We have,
∠AGB and ∠EGD are vertical angles
∠AGB = 30 = ∠EGD
∠CGD and ∠AGF are vertical angles.
∠CGD = 50 = ∠AGF
∠BGC and ∠FGE are vertical angles.
∠BGC = ∠FGE = 2x
We know that,
A straight angle is 180.
∠FGC =180
∠FGC = ∠AGF + ∠AGB + ∠BGC
180 = 50 + 30 + ∠BGC
180 - 50 - 30 = ∠BGC
180 - 80 = ∠BGC
∠BGC = 100
∠FGE = 100
We also see that,
∠FGC = ∠FGE + ∠EGD + ∠CGD
180 = 100 + ∠EGD + 50
180 - 150 = ∠EGD
∠EGD = 30
We see that,
∠EGD = 30°
∠AGB = 30°
Thus, the angle ∠AGB and ∠EGD are equal angles / opposite angles / vertical angles.
Learn more about Vertical angles here:
https://brainly.com/question/24460838
#SPJ1
Function g is the result of these transformations on the parent sine function: vertical stretch by a factor of 3 horizontal shift left units vertical shift down 4 units Substitute the values of A, C, and D to complete the equation modeling function g
Answers
The equation modeling function g after the given transformations on the parent sine function is:
g of (x) = A x sine(C(x minus D))+k
where A is the vertical stretch factor, C is the reciprocal of the horizontal stretch factor, D is the horizontal shift, and k is the vertical shift.
Substituting the given values, we get:
g of (x) = 3*sine((1/1)(x+1))+(-4)
Simplifying further, we get:
g of (x) = 3*sine of (x+1)-4
Therefore, the equation modeling function g is g of (x) = 3*sine(x+1)-4 after the given transformations on the parent sine function.
Learn more about Functions:
https://brainly.com/question/25638609
#SPJ4
Factorise
y²-2y-48
Answers
Answer: y²-2y-48=(y-8)(y+6)
Step-by-step explanation:
\(y^2-2y-48=\\\\y^2-8y+6y-48=\\\\y(y-8)+6(y-8)=\\\\(y-8)(y+6)\)
Answer:
y²-2y-48=(y-8)(y+6)
Step-by-step explanation:by factorization
y2-2y-48= y2-8y+6y48= y(y-8)+6(y-8)= (y-8)(y+6)
I searched it up but didn’t get the right help so now I’m asking
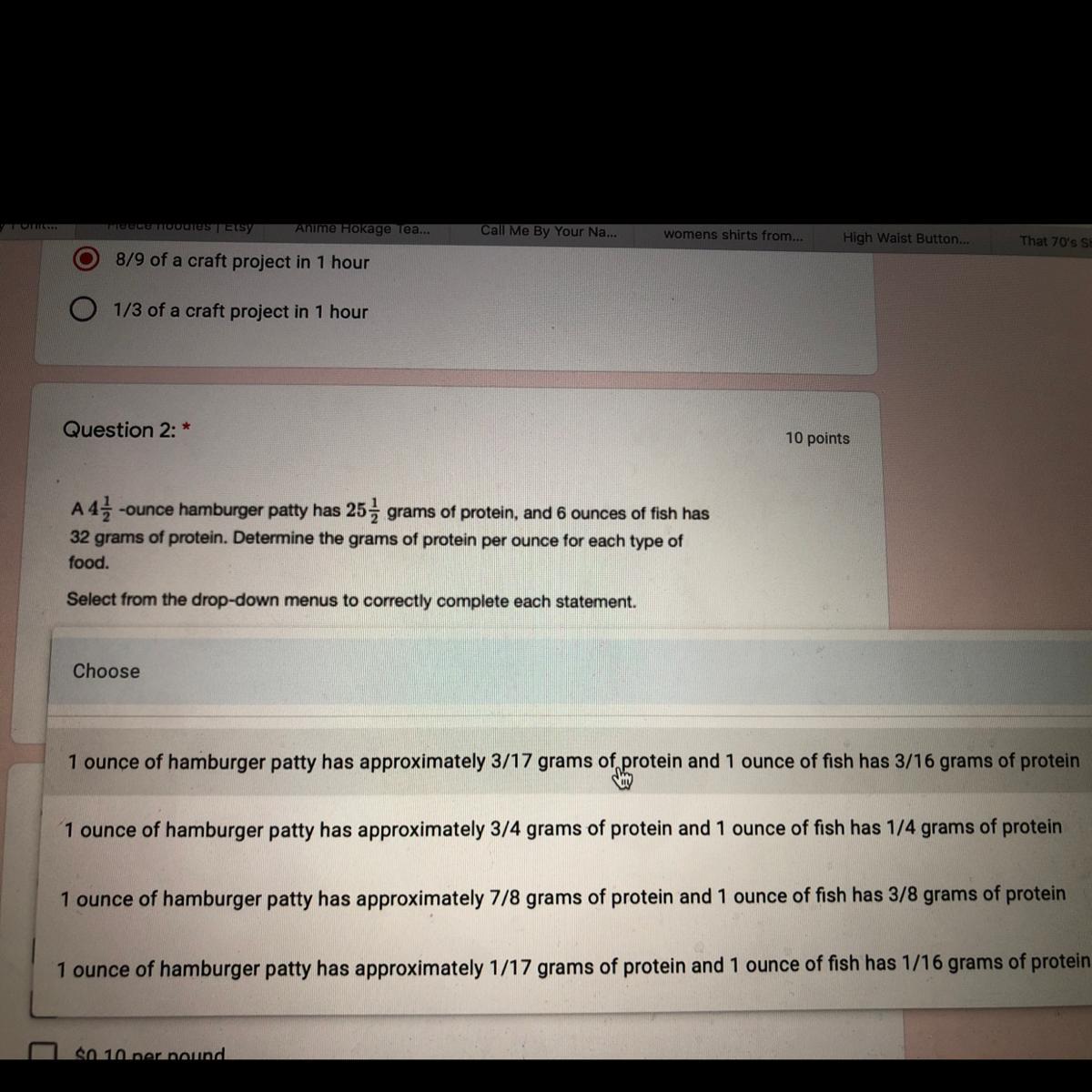
Answers
It should be A: 1 ounce of hamburger patty has approximately 3/17 grams of protein and 1 ounce of fish has 3/16 grams of protein.
3. Use the following diagram to solve for x.
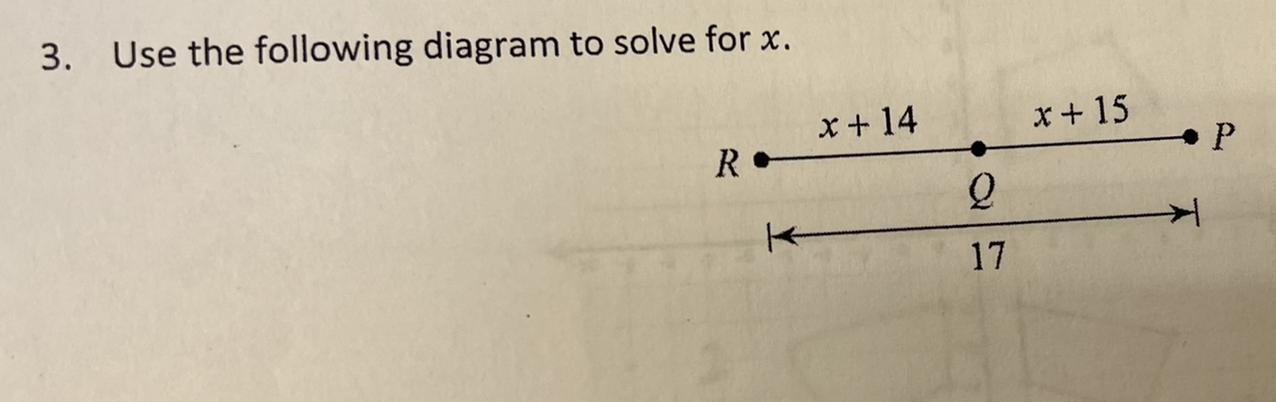
Answers
The value of x from the given diagram is -6
Lines and anglesLine is defined as the distance between two points. Given the line RP with the following measures
RP = 17
RQ = x + 14
QP = x + 15
Using the expression
RP = RQ + QP
Substitute
17 = x + 14 + x + 15
17 = 2x + 29
Determine the value of x
2x = 17 - 29
2x= -12
x = -6
Hence the value of x from the given diagram is -6
Learn more on lines here: https://brainly.com/question/6950210
#SPJ1
Determine the solution to the equation. 8+4x=2x+8+2x A Infinite B One Solution C No Solution
Answers
After solving the given equations the answer is an Infinite solution. Hence, option A is correct
What is an equation?Mathematical expressions with two algebraic symbols on either side of the equal (=) sign are called equations.
This relationship is illustrated by the left and right expressions being equal to one another. The left-hand side equals the right-hand side is a basic, straightforward equation.
As per the given equation in the question,
8 + 4x = 2x + 8 + 2x
Firstly, let's write the given equation in a simplified manner,
8 + 4x = 8 + 4x
As we can see that LHS = RHS, which means that both equations are the same then which means they will give infinite solutions.
To know more about equation:
https://brainly.com/question/29657983
#SPJ1
Select all of the factions that are equivalent to -2/3
Answers
Answer:
-4/6, -8/12, -16/24, etc. look at the picture.
Step-by-step explanation:
Brainliest Please!!! Also, Tip: show the multiple choice options.

Answer:
4/6
Step-by-step explanation:
g the number of bacteria in a culture increases from 600 to 1800 in 2 hours. assuming the rate of increase is proportional to the number of bacteria present, find:
Answers
The rate of increase of the number of bacteria is 1200/2 = 600 bacteria/hour.
To find the rate of increase of the number of bacteria in a culture, we can use the formula
rate of change = change in number of bacteria/time elapsed.
In this case, the change in number of bacteria is 1800-600 = 1200, and the time elapsed is 2 hours.
Thus, the rate of increase of the number of bacteria is 1200/2 = 600 bacteria/hour.
For more such questions on Rate of change.
https://brainly.com/question/30809500#
#SPJ11
Last year at science camp there were 140 people sleeping in cabins. There were 18 students for every 2 chaperones. How many students were sleeping in
cabins?
Answers
Answer:
126 students
Step-by-step explanation:
18+2=20
140 divided by 20=7
7x18=126
140-126=14 chaperones
Find the first three nonzero terms of the Maclaurin series for the function and the values of x for which the series converges absolutely f(x)=(2 sin x) In (1 + x) What are the first three nonzero terms of the Maclaurin series for f(x)?
Answers
The first three nonzero terms of the Maclaurin series for the function f(x) = (2 sin x) ln(1 + x) are: 2x - (2/3)x^3 + (4/45)x^5. The Maclaurin series converges absolutely for all values of x within the interval -1 < x ≤ 1.
To find the Maclaurin series for f(x), we need to express the function as a power series centered at x = 0. We can do this by using the known Maclaurin series expansions for sin x and ln(1 + x).
The Maclaurin series expansion for sin x is:
sin x = x - (1/3!)x^3 + (1/5!)x^5 - ...
The Maclaurin series expansion for ln(1 + x) is:
ln(1 + x) = x - (1/2)x^2 + (1/3)x^3 - ...
Multiplying these two series, we obtain the Maclaurin series expansion for f(x):
f(x) = (2 sin x) ln(1 + x) = 2x^2 - (2/3)x^3 + (4/45)x^5 - ...
The first three nonzero terms of the Maclaurin series for f(x) are: 2x - (2/3)x^3 + (4/45)x^5.
To determine the values of x for which the series converges absolutely, we need to consider the interval of convergence. In this case, the Maclaurin series converges absolutely for all values of x within the interval -1 < x ≤ 1.
To learn more about Maclaurin series Click Here: brainly.com/question/31745715
#SPJ11