Look at the graph on the right. What is the constant rate of change for the relationship shown on the graph?

Answers
For the graph the constant change of rate is 1
The slope of the lines es equal to one
Related Questions
The 10 passengers on a small airplane have paid a total of $1,580 for the flight.
If an economy ticket cost $135 and a first-class ticket costs $250 , how many economy tickets were bought?
Answers
Answer:
8 people bought economy and 2 bought first class
Step-by-step explanation:
there are 10 person and total is 1580 so 250+ 9(135)=1460 which is wrong so we gonna try adding 2(250) and 8(135) which got us 1580
• Riley and her sister collect stickers. Riley has 220 stickers
in her sticker collection. Her sister has 55 stickers in her
collection. Riley has how many times as many stickers as
her sister? Use mental math or the guess, check, and
revise strategy to solve the equation 55x = 220.
Answers
Answer:
Riley has 4 times the amount of stickers her sister has
Step-by-step explanation:
220 divided by 55 is 4
Does the equation Axequalsb have a solution for each b in set of real numbers RSuperscript 4? A. No, because A has a pivot position in every row. B. Yes, because the columns of A span set of real numbers RSuperscript 4. C. Yes, because A does not have a pivot position in every row. D. No, because the columns of A do not span set of real numbers R
Answers
Answer:
C. Yes, because A does not have a pivot position in every row.
Step-by-step explanation:
The pivot position in the matrix is determined by entries in non zero rows. The pivot position may be in the row or a column. By Invertible Matrix Theorem the equation Axequalsb has non trivial solution. A has fewer pivot positions therefore A is not invertible. Ax will map RSuperscript into real numbers for n times. A has pivot position if left parenthesis bold x right parenthesis.
What is the approximate value of θ if tan θ = 7/9
Answers
Answer:
37.9°-----------------------
Taking the inverse tangent (arctan) of the given ratio 7/9.
Use a calculator or trigonometric table to find:
θ ≈ arctan(7/9)The approximate value of θ is 37.9°.
A fraternity charge $2.00 admission for dudes and $1.00 admission for ladies. They made $45 and sold 35 tickets how many ladies attended the party
Answers
After solving the equations, we know that a total of 25 ladies attended the party.
What are equations?A mathematical statement that has an "equal to" symbol between two expressions with equal values is called an equation.
As in 3x + 5 Equals 15, for instance.
Equations come in a variety of forms, including linear, quadratic, cubic, and others.
So, take dudes as x and ladies as y.
Now, form the required 2 equations as follows:
2x + y = 45 ...(1)
x + y = 35 ...(2)
Work on equation (2):
x + y = 35
x = 35 - y
Now, substitute x = 35 - y in equation (1):
2x + y = 45
2(35-y) + y = 45
70 - 2y + y = 45
-y = -25
y = 25
Since ladies were charged $1 for each ticket, then 25 ladies attended the party.
Therefore, after solving the equations, we know that a total of 25 ladies attended the party.
Know more about equations here:
https://brainly.com/question/28937794
#SPJ1
Copy machine makes 44 copies per minute. How long does it take to make 231 copies?
Answers
Answer:
5.25 minutes
Step-by-step explanation:
what is the diameter

Answers
Answer:
9.61m
Step-by-step explanation:
to find the diameter you have to multiply the radius by 2
since radius is half of a circle
If f (x) = -2(x + 7), then what is f (3)?

Answers
Answer:
F(3)=-20
Step-by-step explanation:
just plug 3 for x.
a tip of $10 is typically suitable for which kind of service?
a mover delivering furniture
a valet who parks your car
a waiter at a fast food restaurant
Answers
ax - b = c for x. ..........................
Answers
Answer:
17 for x
Step-by-step explanation:
pls give me brainliest im almost lvled up
Answer:x=\(\frac{c+b}{a}\)
ax-b=c
add b
ax-b+b=c+b
ax=c+b
divide a
ax÷a=c+b÷a
x=\(\frac{c+b}{a}\)
I hope this is good enough:
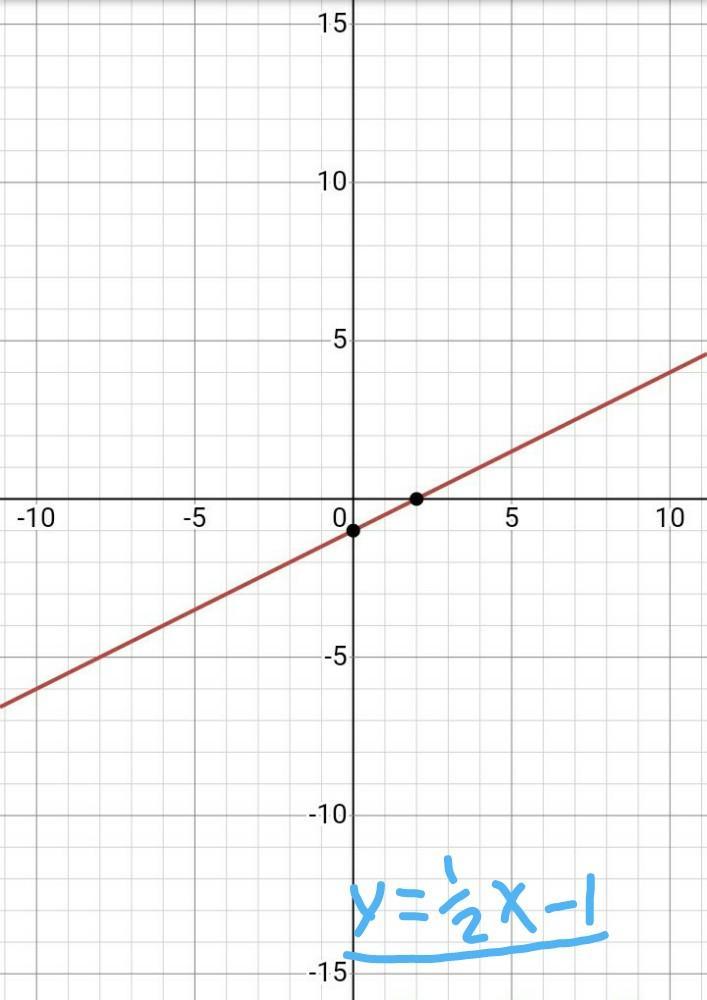
Graph thee line that represents this equation:
y+2=1/2(x+2)

Answers
Answer:
\(y = \frac{1}{2} x - 1\)
Explanation:
The first pic shows the line graphed, while the second pic shows how to turn the equation into proper slope-intercept form.
The only steps the second pic is missing however, is flipping the sides around to be better understood (optional), and more importantly subtracting 2 on both sides in order to move it to the other side, to get 2y = x - 2. And dividing the 2 on both sides to get y by its self, to get:
y = (x-2)/2 , or y = 1/2 x - 2/2 , which if you notice 2/2 makes it equal to one whole so your answer is y = 1/2 x - 1 .
If you like this answer can you please mark me brainliest? :)

you enclose a field using sections of fence with lengths of 9, 12, and 15 meters. Estimate the area of the field.
Answers
The estimated area of the field enclosed by the fence is approximately 220.5 square meters.
What is the Pythagorean theorem?A basic geometry theorem that explains the relationship between a right triangle's three sides is known as the Pythagorean theorem.
We can employ the following strategy to determine how much of the field the fence is enclosing:
Include the lengths of the fence sections in a rough sketch of the field.
Make a straightforward polygon that resembles the field's shape using the fence sections.
To calculate the area of the triangle-shaped portion of the field, use the triangle's area formula (\(A = 1/2 \times base \times height\)). We must identify the triangle's base and height in order to accomplish this.
The Pythagorean theorem can be used to calculate the triangle's height: \(a^2 + b^2 = c^2\)where a and b are the triangle's two shorter sides (9 meters and 12 meters, respectively), and c is the longest side (15 meters). When we solve for (a), we see that it is equal to
(a)
\(= \sqrt{(c^2 - b^2)} \\= \sqrt{(15 2 - 12 2}) \\= \sqrt{(81)} \\= 9 meters.\\\)
The triangle is therefore 9 meters tall. The 9-meter fence portion serves as the triangle's base.
When we apply the triangle's area formula, we obtain:
A is equal to half of the base plus the height, or 9 meters plus 9 meters, or 40.5 square meters.
The area of the remaining field must be increased by the area of the triangle. This estimate may not be very exact because we have just estimated the field's form, but it should at least give us a general notion of the field's size.
If the remaining area of the field has a roughly rectangular form, we can calculate its area by multiplying the rectangle's length and width. The 12-meter and 15-meter fence sections can be used as a guide to determine the rectangle's size.
By dividing the width by the length, we obtain:
180 square meters is the size of the remaining part (12 meters times 15 meters).
To determine the approximate total size of the field, add the areas of the rectangle and triangle portions:
Total area estimated: 40.5 square meters plus 180 square meters, which equals 220.5 square meters.
As a result, the field's approximate area inside the barrier is 220.5 square meters.
To learn more about Pythagorean theorem, Visit
https://brainly.com/question/343682
#SPJ1
I WILL GIVE BRAINLYIST IF UR QUICK ITS TIMEDDDD TOOOOO

Answers
Answer:
B I belive
Step-by-step explanation:
can you help me with my math
5! + 50
Answers
Answer:
170
Step-by-step explanation:
\(5!+50\\\\(5*4*3*2*1)+50\\\\120+50\\\\170\)
Question
5! + 50
Step-by-step explanation:
about factorial
5!
=5 × 4 × 3 × 2 × 1
=20 × 3 × 2 × 1
=60 × 2 × 1
=120 × 1
=120
the result of the factorial 5! is 120
now we just add 120+50
120 + 50
120
50
———+
170
so the result of 5! + 50 is 170
I hope this helps
Chad created a table that shows the ratio of his sports game cards.Next, Chad created the graph below showing possible ratios for Pitchers cards to Infield cards in his deck. Which of the following statements are true?

Answers
Answer:
The 3rd answer is correct.
Step-by-step explanation:
The question involves a mathematical understanding of graphs and data interpretation, specifically ratios. To answer a question like this, typically, you would need to analyze both the graph and table for consistent ratio values. Though the question specifics are unclear, the broader concept involves understanding how ratios can be graphically represented.
Explanation:Given that the question involves ratios and cards, it appears to fall under a mathematical scope, specifically the interpretation of graphs and data. However, the information provided doesn't give specific details about Chad's data, the ratios of his sports game cards, or the graph he created that shows the possible ratios for Pitchers cards to Infield cards.
Typically, to validate any findings, you would need to look at the graph and the table. Comparing the values of the ratios in the table to the characteristics of the graph would help substantiate any claims. For instance, if Chad's graph shows that there's a 1:2 ratio of pitcher cards to Infield cards, this should be reflected in the table of his sports game cards.
Despite the ambiguous details in the question, you can still grasp the concept of ratios and how they can be represented graphically. For example, if you have a 3:5 ratio of oranges to apples, this can be depicted on a graph where one unit on the Y-axis represents 3 oranges and the corresponding unit on the X-axis signifies 5 apples.
Learn more about Ratios and Graph Interpretation here:https://brainly.com/question/33676187
#SPJ2
55 POINTS QUICK PLS Your friend is able to invest $120 a month in a 401(k) with a predicted growth rate of 3%. Your friend's company will match 50% of your friend's contributions.

Answers
a. The monthly contribution from a friend's company is $120 minus 0.5, or $60.
b. The total monthly contribution to the fund is $180.
The computation of FV in Excel is shown in the attachment below:
What is meant by growth rate?Using the current number as a starting point, subtract the prior value to determine the growth rate. To calculate the growth rate in percentage terms, divide the difference by the previous amount and multiply the result by 100. Growth Rate equals (Ending Value - Beginning Value) - 1. The year-over-year (YoY) growth rate of a business, for instance, would be 20% if its revenue increased from $100 million in 2020 to $120 million in 2021.
GDP, turnover, wages, etc., all have growth rates that reflect how much they have changed over time (month, quarter, year). Percentages are a pretty common way to communicate it.
20 years is the age.
20 times 12 periods equals 240.
3% growth rate
The computation of FV in Excel is shown in the attachment below:
So, FV= $7,223,115.77
To know more about growth rate, visit:
https://brainly.com/question/11743945
#SPJ1

How dum are u ??????????????????????
Answers
Answer:
very
Step-by-step explanation:
my brain is very smooth
How many
1/4-foot cubes would fill the inside of the prism?
Write the answer in the box.

Answers
There are 4 cubes of size 1/4 foot would fill the inside of the prism.
We have to given that;
Height of cuboid = 3 feet
Length of cuboid = 3/4 feet
Width of cuboid = 1/2 feet
We know that;
Volume of cuboid = Length x width x height
Hence,
V = 3/4 x 3 x 1/2
V = 9/8
Thus, Number of 1/4-foot cubes which would fill the inside of the prism is,
= (9/8) ÷ (1/4)
= (9/8) x 4
= 9/2
= 4.5
Thus, There are 4 cubes of size 1/4 foot would fill the inside of the prism.
Learn more about the cuboid visit:
https://brainly.com/question/26403859
#SPJ1
how many ping pong balls do you need if you want to arrange them in the shape of an equilateral triangle with 23 rows
Answers
You would need a total of 276 ping pong balls
Step by step explanation:
To determine the number of ping pong balls needed to form an equilateral triangle with 23 rows, we can calculate the total number of balls in the triangle. In an equilateral triangle, each row has one more ball than the previous row. The formula for the sum of the first n natural numbers is given by:
Sum = (n * (n + 1)) / 2
In this case, we want to find the sum of the first 23 natural numbers. Substituting n = 23 into the formula, we get:
Sum = (23 * (23 + 1)) / 2 = 276
Therefore, you would need 276 ping pong balls to arrange them in the shape of an equilateral triangle with 23 rows.
A rectangular flower bed is 7 m long. If the boundary
around the bed is 22 m long, find its breadth. Also,
find its area.
need full solution
Answers
As we know that
\(\sf \blue{Perimeter = 2(l + b)}\)
22 = 2(7 + b)22 = 14 + 2b 22 - 14 = 2b8 = 2b\(\sf \: \dfrac{8}{2} = b\)\(\bold{\boxed{b=4} }\) Breadth = 4 m.Now,
\(\sf \orange{Area = l \times b}\)
\(Area = 7 \times 4\)\(\sf \: Area = 28 \: {m}^{2}\)Area=28\(\bold{ m^2 }\)
Solve the given equation by completing the square.
Fill in the values of a, b, and e to complete the solutions.

Answers
The solution in this case is x = (4 + sqrt(102+4c))/2 - 4√c, which can be expressed in the form of X = a - b√c.
How to solve quadratic equation?
To solve the equation x²+8x-38=0, we can use the quadratic formula:
x = (-b ± sqrt(b²-4ac)) / 2a
Here, a=1, b=8, and c=-38. Substituting these values into the formula gives:
x = (-8 ± sqrt(8²-4(1)(-38))) / 2(1)
x = (-8 ± sqrt(324)) / 2
x = (-8 ± 18) / 2
So x is either -13 or 5.
To find the values of x in the form of X = a + b√c and X = a - b√c, we can use the following steps:
For X=a+b√c:
Let's assume that x = a + b√c, where a, b, and c are constants to be determined.
Substituting this into the original equation x²+8x-38=0, we get:
(a + b√c)² + 8(a + b√c) - 38 = 0
Expanding the square and simplifying, we get:
(a² + 2ab√c + b²c) + 8a + 8b√c - 38 = 0
Separating the real and imaginary parts, we get:
(a² + b²c + 8a - 38) + (2ab√c + 8b)√c = 0
Since the real and imaginary parts of the equation must both be zero, we can set them each equal to zero and solve for a, b, and c.
First, setting the real part equal to zero gives:
a² + b²c + 8a - 38 = 0
This is a quadratic equation in a, so we can use the quadratic formula:
a = (-8 ± sqrt(8²-4(bc-38))) / 2
Simplifying this gives:
a = -4 ± sqrt(4+b(b-10))
Now, setting the imaginary part equal to zero gives:
2ab + 8b = 0
Solving for b, we get:
b = 0 or b = -4
If b = 0, then a² + b²c + 8a - 38 = a² + 8a - 38 = 0, which has roots a = -5 and a = 3. Therefore, the solution in this case is x = -5 or x = 3, which cannot be expressed in the form of X = a + b√c.
If b = -4, then a² + b²c + 8a - 38 = a² + 16c + 8a - 38 = 0. Plugging this into the quadratic formula for a, we get:
a = -4 ± sqrt(102-4c)/2
Therefore, the solution in this case is x = (-4 + sqrt(102-4c))/2 - 4√c, which can be expressed in the form of X = a + b√c.
For X=a-b√c:
Using the same logic, we can assume that x = a - b√c, where a, b, and c are constants to be determined.
Substituting this into the original equation x²+8x-38=0, we get:
(a - b√c)² + 8(a - b√c) - 38 = 0
Expanding the square and simplifying, we get:
(a² + b²c - 8a - 38) + (-2ab√c - 8b)√c = 0
Since the real and imaginary parts of the equation must both be zero, we can set them each equal to zero and solve for a, b, and c.
Setting the real part equal to zero gives:
a² + b²c - 8a - 38 = 0
This is a quadratic equation in a, so we can use the quadratic formula:
a = (8 ± sqrt(8²+4(bc+38))) / 2
Simplifying this gives:
a = 4 ± sqrt(4+b(b+10))
Setting the imaginary part equal to zero gives:
-2ab - 8b = 0
Solving for b, we get:
b = 0 or b = -4
If b = 0, then a² + b²c - 8a - 38 = a² - 8a - 38 = 0, which has roots a = -3 and a = 11. Therefore, the solution in this case is x = -3 or x = 11, which cannot be expressed in the form of X = a - b√c.
If b = -4, then a² + b²c - 8a - 38 = a² + 16c - 8a - 38 = 0. Plugging this into the quadratic formula for a, we get:
a = 4 ± sqrt(102+4c)/2
Therefore, the solution in this case is x = (4 + sqrt(102+4c))/2 - 4√c, which can be expressed in the form of X = a - b√c.
To know more about Equation visit :-
https://brainly.com/question/22688504
#SPJ1
I GIVEEE BRAINLILSTTT

Answers
Answer:
it's a reduction because it's smaller than the original shape
Step-by-step explanation:
(a reduction means the new shape is smaller than the original, and an enlargement means the new shape is bigger than the original one)
Answer:
Step-by-step explanation:
reduction
y=9/4×2
sketch the graph of f and f on the same set of axes
Answers
The graph of the function \(f(x) = (9/4)x^2\) is a symmetric upward-opening parabola.
The graph represents a parabola that opens upward. As x increases, the corresponding y-values increase, forming a curved shape. The vertex of the parabola is at the origin (0,0). The graph is symmetric with respect to the y-axis, meaning that the left and right sides of the parabola are mirror images of each other.The slope of the graph gradually increases as x moves away from the origin. The steepness of the curve becomes more pronounced, indicating a faster rate of increase in y-values for larger x-values.The graph does not intersect the x-axis, indicating that there are no real roots or solutions for the equation f(x) = 0. The y-intercept of the graph is at (0, 0), and the y-values increase indefinitely as x approaches positive or negative infinity.Overall, the graph represents a quadratic function with a positive leading coefficient, resulting in an upward-opening parabolic curve. The graph has been attached.
For more questions on graph:
https://brainly.com/question/19040584
#SPJ8

Carleigh, Inc., is a pork processor. Its plants, located in the Midwest, produce several products from a common process: sirloin roasts, chops, spare ribs, and the residual. The roasts, chops, and spare ribs are packaged, branded, and sold to supermarkets. The residual consists of organ meats and leftover pieces that are sold to sausage and hot dog processors. The joint costs for a typical week are as follows: Direct materials $84,500 Direct labor 29,000 Overhead 20,000 The revenues from each product are as follows: sirloin roasts, $68,000; chops, $71,000; spare ribs, $33,000; and residual, $9,800. Carleigh’s management has learned that certain organ meats are a prized delicacy in Asia. They are considering separating those from the residual and selling them abroad for $52,000. This would bring the value of the residual down to $2,650. In addition, the organ meats would need to be packaged and then air freighted to Asia. Further processing cost per week is estimated to be $27,500 (the cost of renting additional packaging equipment, purchasing materials, and hiring additional direct labor). Transportation cost would be $12,100 per week. Finally, resource spending would need to be expanded for other activities as well (purchasing, receiving, and internal shipping). The increase in resource spending for these activities is estimated to be $3,120 per week.
Answers
Carleigh, Inc. should separate the organ meats from the residual and sell them abroad, as it would increase their total revenue by $17,150 per week.
To determine whether Carleigh, Inc. should separate the organ meats and sell them abroad, we need to calculate the incremental revenue and incremental costs associated with this decision.
The incremental revenue would be the revenue generated from selling the organ meats abroad, which is $52,000 per week. The incremental cost would include the cost of further processing ($27,500 per week), transportation cost ($12,100 per week), and the increase in resource spending for other activities ($3,120 per week).
Therefore, the incremental cost would be $42,720 per week. Subtracting this from the incremental revenue of $52,000, we get an incremental profit of $9,280 per week.
However, this decision would also decrease the value of the residual from $9,800 to $2,650 per week. Therefore, we need to subtract this decrease in value from the incremental profit. This gives us a net increase in profit of $17,150 per week ($9,280 - $7,130).
Thus, it would be beneficial for Carleigh, Inc. to separate the organ meats and sell them abroad.
To learn more about incremental revenue, here
https://brainly.com/question/28167612
#SPJ1
i need help with a question on cylinders ASAP please

Answers
the length of the radius of the cylindrical can will be 5 cm approx.
What is volume?Volume, which is measured in cubic units, is the 3-dimensional space occupied by matter or encircled by a surface. The cubic meter (m3), a derived unit, is the SI unit of volume. Volume is another word for capacity.
Given, You have a can that is in the shape of a cylinder. It has a volume of about 1,728 cubic centimeters. The height of the can is 22 centimeters.
From the general formula of the volume of cylinder:
Volume = pi * r² *h
Where r = radius
h = height
in our case
1728 = 3.14 * radius² * 22
radius² = 1728/3.14*22
radius = √25.01
radius = 5.004
Therefore, the length of the radius of the cylinder will be 5 cm approx.
Learn more about Volume here:
https://brainly.com/question/1578538
#SPJ1
Write the slope-intercept form of the line that
has a slope of −5, and passes through the
point (−4, 3)
Answers
Answer:
Step-by-step explanation:
y - 3 = -5(x + 4)
y - 3 = -5x - 20
y = -5x - 17
Solve the equation by using the quadratic formula.
3 x squared minus 1 = 7 x

Answers
Answer:
b. \(\frac{7+\sqrt{61} }{6} ,\frac{7-\sqrt{61} }{6}\)
Step-by-step explanation:
\(3x^{2} -1=7x\)
Quadratic equations are suppose to be written as: \(ax^2+bx+c=0\)
so the new quadratic equation for this problem will be: \(3x^{2} -1-7x=0\)
Now rearrange the terms: \(3x^{2} -7x-1=0\)
Then use the Quadratic Formula to Solve for the Quadratic Equation
Quadratic Formula = \(x=\frac{-b±}{} \frac{\sqrt{b^2-4ac} }{2a}\)
Note: Ignore the A in the quadratic formula
Once in standard form, identify a, b and c from the original equation and plug them into the quadratic formula.
\(3x^{2} -7x-1=0\)
a = 3
b = -7
c = -1
\(x=-(-7)±\frac{\sqrt{(-7)^2-4(3)(-1)} }{2(3)}\)
Evaluate The Exponent
\(x=\frac{7±\sqrt{(49)-4(3)(-1)} }{2(3)}\)
Multiply The Numbers
\(x=\frac{7±\sqrt{49+12} }{2(3)}\)
Add The Numbers
\(x=\frac{7±\sqrt{61} }{2(3)}\)
Multiply The Numbers
\(x=\frac{7±\sqrt{61} }{6}\)
5/6 having denominator 35
Answers
Answer:( 175/6)
Step-by-step explanation: 5*35/6=175/6 sour our numerator is 175/6. So sour answer is (175/6)/35
Which one of these formulas describes the following sequence?
1,5,12,22,35
Answers
We can find a formula for nth term of the given sequence as follows:
1, 5, 12, 22, 35
The 1st differences between terms:
4, 7, 10, 13
The 2nd differences :
3, 3, 3
Since it takes two rounds of differences to arrive at a constant difference between terms, the nth term will be a 2nd degree polynomial of the form: \(a n^2 + b n + c\), where c is a constant. The coefficients a, b, and the constant c can be found.
We can form the following 3 equations with 3 unknowns a, b, c:
\(1 = a\cdot1^2 + b\cdot1 + c\\5 = \cdot2^2 + b\cdot2 + c\\12 = a\cdot3^2 + b\cdot3 + c\)
Solving for a, b, c, we get:
a = 3/2, b = -1/2, c = 0
Therefore, the nth term of the given sequence is:
\(\boxed{ a_n = \dfrac{3}{2}n^2- \dfrac{1}{2} n}\)
In a lab, a substance was heated by 2°C each hour for 10 hours. What was the total change in temperature?
Answers
Answer:20
Step-by-step explanation:2 times with 10 hours becase per hour the temperature 2 degree celsius