lets pretend it takes 30 sumerians 10 days to dig a mile long canal. Now they needed to dig 400 miles of canals in 12 weeks, how many people would they need to do the work in time

Answers
We need \(1429\) employees to accomplish the task in \(12 week\) time frame
\(1\) \(miles\) canal dig on \(10 days\) by \(30\) Sumerians\(miles\)
\(400 miles\) can dig by how many people
\(400 km\) times \(30\) Sumerians times \(10 days\) is \(120000 person per days\)
∴\(12 weeks ( 84 days)\) the following person required\(\frac{120,000}{84} = 1429\) employees
Therefore \(1429\) employees are required to accomplish the task in \(12 week\) time frame.
Learn more about time and work
https://brainly.com/question/3854047
#SPJ1
Related Questions
Perimeter is 25 cm, find x 10 8.2 cm
Answers
Michael bought a box of 20 pretzel rods for 4.40 what is the price per pretzel rod
Answers
Just do 20 divided by 4.40
How far is 75% of 2000 km trip
Answers
Answer:
1, 500km
Step-by-step explanation:
\( \frac{75}{100} \times 2000 \\ \\ = 1500\)
Answer: 1,500km
Step-by-step explanation:
63 divided by 4914
Answers
Answer:
1/78
Decimal form:
0.0 128205...
hope this helps!
urn a contains six white balls and seven black balls. urn b contains five white balls and three black balls. a ball is drawn from urn a and then transferred to urn b. a ball is then drawn from urn b. what is the probability that the transferred ball was white given that the second ball drawn was white?
Answers
Using the Bayes' theorem, we find the probability that the transferred ball was white given that the second ball drawn was white to be 52/89, or approximately 0.5843.
To solve this problem, we can use Bayes' theorem, which relates the conditional probability of an event A given an event B to the conditional probability of event B given event A:
P(A|B) = P(B|A) * P(A) / P(B)
where P(A|B) is the probability of event A given that event B has occurred, P(B|A) is the probability of event B given that event A has occurred, P(A) is the prior probability of event A, and P(B) is the prior probability of event B.
In this problem, we want to find the probability that the transferred ball was white (event A) given that the second ball drawn was white (event B). We can calculate this probability as follows:
P(A|B) = P(B|A) * P(A) / P(B)
P(B|A) is the probability of drawing a white ball from urn b given that the transferred ball was white and is now in urn b. Since there are now six white balls and three black balls in urn b, the probability of drawing a white ball is 6/9 = 2/3.
P(A) is the prior probability of the transferred ball being white, which is the number of white balls in urn a divided by the total number of balls in urn a, or 6/13.
P(B) is the prior probability of drawing a white ball from urn b, which can be calculated using the law of total probability:
P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
where P(B|not A) is the probability of drawing a white ball from urn b given that the transferred ball was black and P(not A) is the probability that the transferred ball was black, which is 7/13.
To calculate P(B|not A), we need to first calculate the probability of the transferred ball being black and then the probability of drawing a white ball from urn b given that the transferred ball was black.
The probability of the transferred ball being black is 7/13. Once the transferred ball is moved to urn b, there are now five white balls and four black balls in urn b, so the probability of drawing a white ball from urn b given that the transferred ball was black is 5/9.
Therefore, we can calculate P(B) as follows:
P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
= (2/3) * (6/13) + (5/9) * (7/13)
= 89/117
Now we can plug in all the values into Bayes' theorem to find P(A|B):
P(A|B) = P(B|A) * P(A) / P(B)
= (2/3) * (6/13) / (89/117)
= 52/89
Therefore, the probability that the transferred ball was white given that the second ball drawn was white is 52/89, or approximately 0.5843.
To know more about Bayes' theorem refer here :
https://brainly.com/question/29598596#
#SPJ11
question 9
DETAILS REVIOUS ANSWERS 2.1.040. MY NOTES ASK YOUR TEACHER Use a graphing utility to graph the quadratic function. Identify the vertex, axis of symmetry, and x-intercepts. (If there is no intercept, e
Answers
The vertex is (2,14), the axis of symmetry is x = 2, and the x-intercepts are (-1,0) and (5,0).
Given function is \($f(x) = -2x^2 + 8x + 10$\).To find the vertex, axis of symmetry and x-intercepts of the quadratic function \($f(x) = -2x^2 + 8x + 10$\), use a graphing calculator. By using the graphing calculator, we can obtain the following graph.
The quadratic function has its vertex at (2,14) and
the axis of symmetry is the vertical line x = 2.The x-intercepts can be found by setting $y = 0$. Thus, solving the quadratic equation \($f(x) = -2x^2 + 8x + 10 = 0$\) gives the following solutions.\($$-2x^2 + 8x + 10 = 0$$\)Multiply by \($-\frac{1}{2}$\) and
simplify.\($$x^2 - 4x - 5 = 0$$(x-5)(x+1) = 0$$\)
Hence, the x-intercepts are (-1,0) and (5,0).
To know more about vertex,visit:
https://brainly.com/question/32432204
#SPJ11
How much does the state spend in tax dollars altogether?
a. 20 million dollars
b. 12 million dollars
c. 24 million dollars
d. 48 million dollars
Answers
Answer:
24 mill
Step-by-step explanation:
Answer:
24
Step-by-step explanation:
A bag of dry costs $2.85. Alka pays for the bag with a $5.00 bill. How much change does Alka get back?
Answers
Answer:
$2.15
Step-by-step explanation:
$5 - $2.85 = $2.15
this is the explanation
The cost of dry bag is $2.85 then the change does Alka get back will be $2.15.
What are arithmetic Operations?The four fundamental operations of arithmetic are addition, subtraction, multiplication, and division of two or even more items.
Included in them is the study of integers, especially the order of operations, which is important for all other areas of mathematics, notably algebra, data management, and geometry.
As per the mentioned information in the question,
Cost of dry bag = $2.85
Money given by Alka for the bill = $5.00
Then, the amount she will get back,
($5.00 - $2.85) = $2.15
To know more about arithmetic operations:
https://brainly.com/question/25277954
#SPJ2
HELP ME PLZ
Which ordered pairs represent points on the graph of this equation? Select all that apply.
3x + y = 0

Answers
Answer:
(-1,3)
Step-by-step explanation:
Thus;
When (-1,3) is placed in the relation 3x + y =0,the answer will be zero.
CalculationsLet;
x= -1
y= 3
3(-1) + 3 =0
-3 + 3 = 0
(1,-3) ,(-2,6)(2,-6),(-1,3) are ordered pairs represent points on the graph of this equation 3x+y=0.
What is an equation of a line?An equation of the line is defined as the linear equation having a degree of one. The equation of the line contains two variables x and y. And the third parameter is the slope of the line which represents the elevation of the line.
The general form of the equation of the line is y = mx + c, where m is the slope and c is the intercept cut by the y.
To calculate the ordered pair by satisfying the equation with each pair of points.
3x+y=0
For (1,-3)
3(1)-3=0 Yes
For (-2,6)
3(-2)+6=0 Yes
For (2,-6)
3(2)-6=0 Yes
For (-1,3)
3(-1)+3=0 Yes
For (6, -1)
3(6)-1=11 No
For (-6,1)
3(-6)+1=-11 No
Hence (1,-3) ,(-2,6)(2,-6),(-1,3) are ordered pairs represent points on the graph of this equation 3x+y=0.
To learn more on Equations click:
brainly.com/question/18831322
#SPJ2
Determine the minimum rotation (in degrees) which will carry the following figure onto itself ( where all sides and verticles will match up). Round to the nearest tenth if necessary.
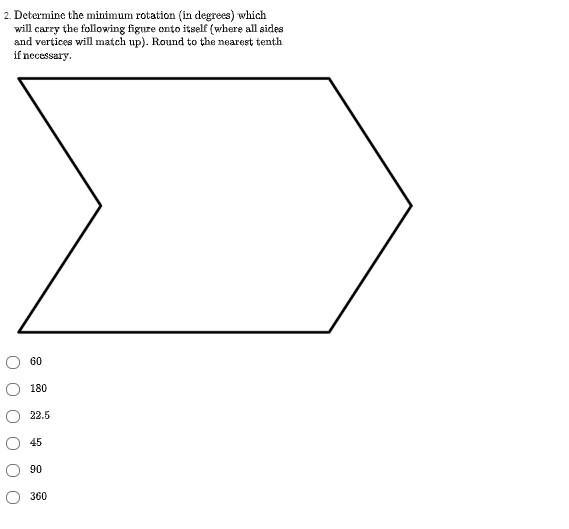
Answers
Answer:
360°
Step-by-step explanation:
The figure is irregular which means it must be completely rotated to have matching sides and vertices. A full rotation is equal to 360°.
problem 3. union coffee shop at njit campus has one barista. students arrive at the rate of 20 students per hour according a poisson distribution. the service time is estimated to be 2 customers per minute (exponentially distributed). 3.1 (10 points) please calculate the average number of customers in the system. (show your work) 3.2 (10 points) what is the probability that exactly 20 customers will arrive in a 1-hour period? (show your work) 3.3 extra credit question (5 points) suppose that a student arrival rate increases to 35 students per hour according a poisson distribution. what dynamics you would observe in the waiting line. how many people would be in the system (both waiting and being served)?
Answers
The average number of people in the system would be 0.41 customers, where the waiting line would be increasing.
This is a queuing theory problem. Average number of customers in the system:
Arrival rate, λ = 20 students/hour
Service rate, μ = 2 customers/minute = 120 customers/hour
Utilization factor, ρ = λ/μ = 20/120 = 1/6
Average number of customers in the system:
L = λ/(μ-λ)
= 20/(120-20)
= 1/5
= 0.2 customers
Probability that exactly 20 customers will arrive in a 1-hour period:
Number of arrivals, X ~ Poisson(λt) = Poisson(20)
Probability of 20 arrivals, P(X=20):
= = (e^(-20) * 20^20) / 20! = 0.026
The waiting line would increase and the number of people in the system would increase as well. The average number of customers in the system, L = λ/(μ-λ) = 35/(120-35) = 7/17 = 0.41 customers.
To know more about queuing problem, refer:
https://brainly.com/question/30022383
#SPJ4
Correct question is:
Union coffee shop at NJIT campus has one barista. Students arrive at the rate of 20 students per hour according to a Poisson distribution. The service time is estimated to be 2 customers per minute (exponentially distributed).
Please calculate the average number of customers in the system. (show your work)
What is the probability that exactly 20 customers will arrive in a 1-hour period? (show your work)
Suppose that a student arrival rate increases to 35 students per hour according a poisson distribution. what dynamics you would observe in the waiting line. how many people would be in the system (both waiting and being served)?
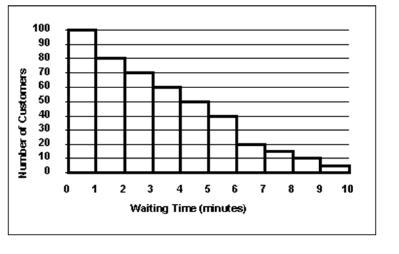
The staff of Mr. Wayne Wertz, VP of Operations at Portland Peoples Bank, prepared a frequency histogram of waiting time for walk-in customers. Approximately how many walk-in customers waited at least 6 minutes? (Note the position of the labels on the x-axis — the first column is the number of customers who waited 1 minute and the last column is the number of customers who waited 10 minutes)
Answers
The number of people who waited at least 6 minutes is given as follows:
50 people.
What is shown by the histogram?The height of each bin of the histogram represents the number of observations of the data-set in the desired interval.
The desired outcomes for this problem are given as follows:
Between 6 and 7 minutes: 20 people.Between 7 and 8 minutes: 15 people.Between 8 and 9 minutes: 10 people.Between 9 and 10 minutes: 5 people.Hence the number of people who waited at least 6 minutes is given as follows:
20 + 15 + 10 + 5 = 50 people.
More can be learned about histograms at brainly.com/question/25983327
#SPJ1
A triangle has two sides of lengths 6 and 9. What value could the length of
the third side be? Check all that apply.
OA. 7
B. 2
C. 4
OD. 15
□E. 10
O F. 12
SUBMIT
Answers
B. 2 and OD. 15 are not possible lengths for the third side of the triangle.
To determine the possible values for the length of the third side of a triangle, we need to consider the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Given that two sides have lengths 6 and 9, we can analyze the possibilities:
6 + 9 > x
x > 15 - The sum of the two known sides is greater than any possible third side.
6 + x > 9
x > 3 - The length of the unknown side must be greater than the difference between the two known sides.
9 + x > 6
x > -3 - Since the length of a side cannot be negative, this inequality is always satisfied.
Based on the analysis, the possible values for the length of the third side are:
A. 7
C. 4
□E. 10
O F. 12
B. 2 and OD. 15 are not possible lengths for the third side of the triangle.
for such more question on lengths
https://brainly.com/question/24176380
#SPJ8
The diameter of a circle is 34 meters. What is the circle's area?
Answers
Answer:
area of a circle = πr^2
So to find the area we need to know the radius. This is easy, as the radius is half of the diameter. So let's half it:
34/2 = 17m
And then substitue 17, for r:
= π(17)^2
= 289π
= 907.9202769m^2
You can round this however you like, but the best options are often either 3 significant figures, either 1 or 2 decimal places.
in a survey conducted on an srs of 200 american adults, 72% of them said they believed in aliens. give a 95% confidence interval for percent of american adults who believe in aliens.
Answers
A 95% confidence interval for percent of american adults who believe in aliens: (0.6578, 0.7822)
In this question we have been given that in a survey conducted on an srs of 200 american adults, 72% of them said they believed in aliens
We need to find the 95% confidence interval for percent of american adults who believe in aliens.
95% confidence interval = (p ± z√[p(1 - p)/n])
Here, n = 200
p = 72%
p = 0.72
And the z-score for 95% confidence interval is 1.960
The upper limit of interval would be,
(p + z√[p(1 - p)/n])
= 0.72 + 1.960 √[0.72(1 - 0.72)/200]
= 0.72 + 1.960 √[(0.72 * 0.28)/200]
= 0.72 + 1.960 √0.001008
= 0.72 + 0.0622
= 0.7822
The lower limit of interval would be,
(p - z√[p(1 - p)/n])
= 0.72 - 1.960 √[0.72(1 - 0.72)/200]
= 0.72 - 1.960 √[(0.72 * 0.28)/200]
= 0.72 - 1.960 √0.001008
= 0.72 - 0.0622
= 0.6578
Therefore, a 95% confidence interval = (0.6578, 0.7822)
Learn more about 95% confidence interval here:
https://brainly.com/question/15683202
#SPJ4
After 7 days, people saw the video.
Answers
Answer:
137,257
Step-by-step explanation:
Answer:
137,527
Step-by-step explanation:
Divide. Give the Quotient and Remainder. 520 / 22
Answers
Answer:
Quotient=23 and remainder=14
3 friends go on a hike and bring 14 cookies with them. If they split them evenly how much will each get
Answers
14÷3= 4.6666666...
so 4 cookies for each one... with 2 cookies left
Henry made a scale model of a submarine. The submarine has an actual height of 75 feet. Henry’s model used a scale in which 1 inch represents 5 feet. What is the height in inches of Henry's model?
Answers
Answer: 180 Inchs
Reason:
75 / 5
180 Inchs = 15 Feet
-DoggyMan5
The table below shows the height and the hand span of five students. What pattern of association best describes the relationship between the height and the hand span?
1) no association
2) non linear association
3) positive linear association
4) negative linear association

Answers
Answer:
2
Step-by-step explanation:
2
if ∫3−5f(x)dx=6, and ∫3−5g(x)dx=3 , then ∫3−5[2f(x) 6g(x)]dx=
Answers
The answer to the given problem is ∫3−5[2f(x) 6g(x)]dx = 108. This can be found by using the properties of integration and substituting the given values for the integrals of f(x) and g(x).
Given that:
∫3−5f(x)dx=6
∫3−5g(x)dx=3
We need to find: ∫3−5[2f(x) 6g(x)]dx
To solve this problem, we will use the properties of integration:
Property 1:
If c is a constant, then
∫cf(x)dx=c∫f(x)dx
Property 2:
If f(x) and g(x) are two functions, then
∫[f(x) + g(x)]dx = ∫f(x)dx + ∫g(x)dx
Using Property 1, we can rewrite the given equation as:
∫3−5[2f(x) 6g(x)]dx = ∫3−5[12f(x)g(x)]dx
Using Property 2, we can further simplify the equation as:
∫3−5[12f(x)g(x)]dx = ∫3−5[12f(x)]dx + ∫3−5[12g(x)]dx
Now we can substitute the given values:
∫3−5[12f(x)]dx + ∫3−5[12g(x)]dx = 12∫3−5f(x)dx + 12∫3−5g(x)dx
Substituting the given values for the integrals of f(x) and g(x), we get:
12∫3−5f(x)dx + 12∫3−5g(x)dx = 12(6) + 12(3)
Simplifying, we get:
12∫3−5f(x)dx + 12∫3−5g(x)dx = 12(6) + 12(3) = 12(9) = 108
Therefore, the answer is
∫3−5[2f(x) 6g(x)]dx = 108
The answer to the given problem is ∫3−5[2f(x) 6g(x)]dx = 108. This can be found by using the properties of integration and substituting the given values for the integrals of f(x) and g(x).
the complete question is :
if ∫3−5f(x)dx=6, and ∫3−5g(x)dx=3 , then ∫3−5[2f(x) 6g(x)]dx will be equal to ?
Learn more about integral here
https://brainly.com/question/18125359
#SPJ4
Gerald ordered a small pizza, asked for it to be divided into 8 equal slices and ate 3 of them. Sarah also ordered a small pizza asked it to be divided into 24 slices, and ate 6 of them. Who ate more pizza? ( My sister's 6th grade question, please help her)
Answers
The Gerald ordered and ate more pizza than Sarah .
What is fraction?
A fraction having whole numbers for the numerator and denominator. A fraction is a number of the form: ab where a and b are integers and b≠0. It represents the division of two numbers.
Given:
Gerald ordered a small pizza, divided into 8 equal slices and ate 3 of them.
Sarah also ordered a small pizza ,divided into 24 slices, and ate 6 of them.
According to given question we have
Gerald divided into 8 equal slices and ate 3 of them.
=3/8
Sarah divided into 24 slices, and ate 6 of them.
=6/24
=1/4
Multiply with 2 in both numerator and denominator we get,
=1*2/4*2
=2/8
∴3/8>2/8
So, Gerald ate more pizza.
Therefore, the Gerald ordered and ate more pizza than Sarah .
Learn more details about fraction here:
https://brainly.com/question/10354322
#SPJ1
segment jk has coordinates j(3 -6) and k(-3 2). Find the coordinates of the midpoint M. Find the distance between the endpoints of JK.
Answers
The coordinates of the midpoint M of segment JK are (-0. 3). The distance between the endpoints of JK is sqrt(104) or approximately 10.198.
To find the coordinates of the midpoint M of segment JK, we can use the midpoint formula, which states that the x-coordinate of the midpoint is the average of the x-coordinates of the endpoints and the y-coordinate of the midpoint is the average of the y-coordinates of the endpoints. So, for segment JK with endpoints J(3, -6) and K(-3, 2), the x-coordinate of the midpoint is (-3+3)/2 = 0 and the y-coordinate of the midpoint is (-6+2)/2 = -2. Therefore, the coordinates of the midpoint M are (0, -2).
To find the distance between the endpoints of JK, we can use the distance formula, which states that the distance between two points with coordinates (x1, y1) and (x2, y2) is given by the square root of [(x2-x1)^2 + (y2-y1)^2]. So for segment JK with endpoints J(3, -6) and K(-3, 2), the distance is sqrt[(-3-3)^2 + (2-(-6))^2] = sqrt[36 + 64] = sqrt(100) = 10. Therefore, the distance between the endpoints of JK is approximately 10.198.
Learn more about Midpoint Formula here: brainly.com/question/17685913
#SPJ11
Plz hurry help will mark brainliest if given correct answers.
Consider the segments on the coordinate plane.
Which two statements are true?
A. The length of segment JK is 5 units.
B. The length of segment JK is 10 units.
C. The length of segment PQ is 5 units.
D. The length of segment PQ is 10 units.
E. The length of segment ST is 10 units.
Choose two of the correct answers

Answers
Answer:
Option (A) and Option (E)
Step-by-step explanation:
Length of a segment between two points \((x_1,y_1)\) and \((x_2,y_2)\) is given by,
Length = \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)
Length of the segment between J(-8, 1) and K(-5, 5) will be,
JK = \(\sqrt{(-8+5)^2+(1-5)^2}\)
JK = \(\sqrt{9+16}\)
JK = 5 units
Length of segment between the points P(2, 8) and Q(7, 3) will be,
PQ = \(\sqrt{(2-7)^2+(8-3)^2}\)
PQ = \(\sqrt{25+25}\)
PQ = \(5\sqrt{2}\) units
Length of segment between the points S(-3, -10) and T(3, -2) will be,
ST = \(\sqrt{(-3-3)^2+(-10+2)^2}\)
ST = \(\sqrt{36+64}\)
ST = 10 units
Therefore, Option (A) and Option (E) are the correct options.
Prove 2 n > n 2 by induction using a basis > 4: Basis: n 5 2A 25 Assume: Prove: Enter the rest of your proof in the box below.
Answers
We have proven that if the inequality holds true for k, it also holds true for k + 1. By the principle of mathematical induction, the inequality 2^n > n^2 holds true for all n > 4.
To prove the inequality 2^n > n^2 using induction with a basis greater than 4, we will use n=5 as the basis.
Basis: n = 5
2^5 = 32 and 5^2 = 25. Since 32 > 25, the inequality holds true for n = 5.
Now, we need to assume that the inequality holds true for an arbitrary positive integer k > 4, and then prove that it holds true for k + 1.
Assume: 2^k > k^2 for k > 4.
Prove: 2^(k + 1) > (k + 1)^2
Step 1: Multiply both sides of the assumption by 2.
2 * (2^k) > 2 * (k^2)
Step 2: Simplify the left side of the inequality.
2^(k + 1) > 2k^2
Step 3: Show that 2k^2 is greater than (k + 1)^2 for k > 4.
2k^2 > (k + 1)^2
2k^2 > k^2 + 2k + 1
Step 4: Rearrange the inequality to show that it holds true for k > 4.
k^2 - 2k - 1 > 0
Since k > 4, it is clear that k^2 - 2k - 1 > 0, as the left side increases as k increases.
Therefore, we have proven that if the inequality holds true for k, it also holds true for k + 1. By the principle of mathematical induction, the inequality 2^n > n^2 holds true for all n > 4.
Visit here to learn more about inequality:
brainly.com/question/30231190
#SPJ11
PLEASE help me with this question! No nonsense answers and answer with full solutions please!


Answers
Answer: b) {-3, 0.5}
Step-by-step explanation:
The new equation is the original equation plus 6. Move the original graph UP 6 units. The solutions are where it crosses the x-axis.
\(\text{Original equation:}\quad f(x)=\dfrac{15}{x}-\dfrac{9}{x^2}\\\\\\\text{New equation:}\quad\dfrac{15}{x}+6=\dfrac{9}{x^2}\\\\\\.\qquad \qquad f(x)= \dfrac{15}{x}-\dfrac{9}{x^2}+6\)
+6 means it is a transformation UP 6 units.
Solutions are where it crosses the x-axis.
The curve now crosses the x-axis at x = -3 and x = 0.5.

Write : linear equation to represent the line shown on the graph.

Answers
The equation of the line that passes through the points (0,-2) and (3,2) is 4x-3y-6 = 0.
What is equation of line?A line's equation is an algebraic way of expressing the collection of points that make up a line in a coordinate system.
The many points that collectively make up a line on the coordinate axis are represented as a group of variables (x, y) to create an algebraic equation, also known as an equation of a line.
In the given graph,
The points are (0,-2) and (3,2)
To find the equation of the line,
Find slope by using formula m = (y₂-y₁)/(x₂-x₁)
m = (2-(-2))/(3-0)
m = 4/3
The equation of line is,
y-y₁ = m (x-x₁)
y-(-2) = 4/3(x-0)
y+2 = 4/3x
3y+6 = 4x
4x-3y-6 = 0
The required equation of line is 4x-3y-6 = 0.
To know more about Equation of line on:
https://brainly.com/question/21511618
#SPJ1
For what values of x is the inequality 2/3 + x/3 >1 true?

Answers
Answer:
B
Step-by-step explanation:
\(\frac{2}{3}\) + \(\frac{x}{3}\) > 1 ( multiply through by 3 to clear the fractions )
2 + x > 3 ( subtract 2 from both sides )
x > 1
Given 4 and one tenth times negative 4 times 5 over 12, determine the product.
Answers
The word problem 4 and one tenth times negative 4 times 5 over 12 have a product of negative 8 and one fifth
How to find the product of the word problemMultiplication is one of the basic mathematical operator which is used to solve the given problem. It is the inverse of division. the result of multiplication is called the product
Rewriting the word problem 4 and one tenth times negative 4 times 5 over 12 to figures
4 1/10 * -4 * 5/10
solving the equation
= 4 1/10 * -4 * 5/10
= 41/10 * -4 * 5/10
= -41/5
= -8 1/5
The product of the multiplication is negative 8 and one fifth
Learn more about fractions:
https://brainly.com/question/78672
#SPJ1
The volume of Cylinder A is 189 ft and the
volume of Cylinder B is 56 ft. If the cylinders are
similar, what is the ratio of surface area of
Cylinder A to the surface area of Cylinder B?
Please don’t put in a link
Answers
Answer:
27:8
Step-by-step explanation:
189/56 = 27/8