Let F : ]0, +[infinity][ × R → R be the function F(x, y)=y(e**y +x)-ln(x).
Show: there exists a neighborhood I ⊂ R of the point x0 = 1 and a unique function f :I →R such that.
(1) f(1) = 0 and f ∈ C1(I),
(2) F(x, f(x)) = 0 for all x ∈ I.
( f ∈ C1(I), means that f is differentiable and that the derivative is continuous. )
Answers
The function F(x, y) = y(e^y + x) - ln(x) defines a function f(x) such that f(1) = 0 and F(x, f(x)) = 0 for all x in a neighborhood I of x0 = 1. This function is continuous and differentiable in I.
To show the existence and uniqueness of the function f, we need to demonstrate two conditions. First, f(1) = 0, and second, F(x, f(x)) = 0 for all x in I. We begin by evaluating F at (1, 0) and observe that F(1, 0) = 0(e^0 + 1) - ln(1) = 0, satisfying the second condition.
Next, we consider the partial derivative of F with respect to y, denoted by ∂F/∂y. Computing this derivative yields ∂F/∂y = (e^y + 1)y + 1. Since e^y + 1 is always positive, we can conclude that ∂F/∂y > 0 for all y in the domain. Consequently, ∂F/∂y is strictly increasing and thus invertible. By the inverse function theorem, we can find a neighborhood I of x0 = 1 such that F(x, y) = 0 has a unique solution y = f(x) for each x in I.
Furthermore, since ∂F/∂y is continuous, it follows that f(x) is differentiable. Additionally, the derivative of f(x) can be computed as f'(x) = -∂F/∂x / ∂F/∂y, which is continuous since both ∂F/∂x and ∂F/∂y are continuous functions.
In summary, there exists a neighborhood I of x0 = 1 where the function f(x) = 0 is continuous and differentiable, satisfying both conditions f(1) = 0 and F(x, f(x)) = 0 for all x in I.
Learn more about inverse function theorem here:
https://brainly.com/question/32280880
#SPJ11
Related Questions
A right triangle has a leg that measures 15 ft and the hypotenuse measures 24 ft. What would the
length of the missing leg be to the nearest whole number?
Answers
Answer:
x=19
Step-by-step explanation:
First, you place the numbers in place of the variables in their relative positions using the pythagorean theorem:
\(15^{2} +x^{2}=24^{2}\)
Then you square the numbers that you currently have:
\(225+x^{2}=576\)
Then subtract 225 from both sides to isolate the x:
\(x^{2} =576-225\)
This gives you the equation:
\(x^{2} =351\)
Then take the square root of both sides which gives you:
\(x=18.7349939952\)
Then round to the nearest whole number which gives you x=19
A fish is swimming at a constant rate toward the ocean floor. The equation
y = -7x - 3 can be used to represent this situation, where y is the depth of the fish in meters below sea level and x is the number of seconds the fish has been swimming.
Which statement best describes the depth of the fish, given this equation?
Answers
Answer: Y = 21
Step-by-step explanation:
Which of the following shows the correct first step to solve x^2-18x=-45
A x^2 - 18x + 18= -45 + 18
B. x^2 - 18x + 9 = -45 + 18
C. x^2 -18x + 81 = -45
D. X^2 -18 + 81 = -45 + 81
Answers
Answer:
D, X^2 -18 + 81 = -45 + 81
Step-by-step explanation:
it is complating squer method that used for solving x in a quadratic equetion . in this step you will add
(y/2)^2 if y is the cofitient of x .
In a triangle, one acute angle is 33 degree. The adjacent side of angle 33 degree is 8 and opposite side is x. The largest side of the triangle is 15."/> find the value of x to the nearest tenth
Answers
The value of x, to the nearest tenth, is approximately 4.96. The steps involved using the tangent ratio and solving for the unknown side in a right triangle.
In a triangle, the angle opposite to the side x as angle A, and the side opposite to the angle 33° as side B, and the largest side as side C. So we have:
Angle A = 90° - 33° = 57° (since the sum of angles in a triangle is 180°)
Side B = 8
Side C = 15
Side x = ?
Write the formula for the tangent ratio in terms of the sides of the triangle. For angle A, we have:
tangent(A) = opposite/adjacent
Substitute the known values into the formula and solve for the unknown side. Substituting the values we have, we get
tangent(33°) = x/8
Multiplying both sides by 8, we get:
x = 8 * tangent(33°)
Use a calculator to find the value of the tangent of 33 degrees. We get:
tangent(33°) ≈ 0.6494
Substitute the value of the tangent into the formula we obtained in step 3 and solve for x. We get
x ≈ 8 * 0.6494
x ≈ 5.1952
Round the answer to the nearest tenth, since the question asks for the value of x to the nearest tenth. We get
x ≈ 4.96
Therefore, the value of x, to the nearest tenth, is approximately 4.96.
To know more about Trigonometric Ratio:
https://brainly.com/question/31511603
#SPJ1
a standard die is rolled until a six rolls. each time a six does not roll, a fair coin is tossed, and a running tally of the number of heads minus the number of tails is kept. (for example, if the die rolls are 5, 2, 1, 6, and the coin tosses are h, h, t, then the running tally is 1, 2, 1.) what is the probability that the absolute value of the running tally never equals 3?
Answers
The probability that the absolute value of the running tally never equals 3 is approximately 0.718, or 71.8%. In this scenario, the running tally can only change by 1 each time the coin is tossed, either increasing or decreasing. It starts at 0, and we need to calculate the probability that it never reaches an absolute value of 3.
To find the probability, we can break down the problem into smaller cases. First, we consider the probability of reaching an absolute value of 1. This happens when there is either 1 head and no tails or 1 tail and no heads. The probability of this occurring is 1/2.
Next, we calculate the probability of reaching an absolute value of 2. This occurs in two ways: either by having 2 heads and no tails or 2 tails and no heads. Each of these possibilities has a probability of (1/2)² = 1/4.
Since the running tally can only increase or decrease by 1, the probability of never reaching an absolute value of 3 can be calculated by multiplying the probabilities of not reaching an absolute value of 1 or 2. Thus, the probability is (1/2) * (1/4) = 1/8.
However, this calculation only considers the case of the first coin toss. We need to account for the fact that the coin can be tossed multiple times. To do this, we can use a geometric series with a success probability of 1/8. The probability of never reaching an absolute value of 3 is given by 1 - (1/8) - (1/8)² - (1/8)³ - ... = 1 - 1/7 = 6/7 ≈ 0.857. However, we need to subtract the probability of reaching an absolute value of 2 in the first coin toss, so the final probability is approximately 0.857 - 1/8 ≈ 0.718, or 71.8%.
Learn more about probability here: https://brainly.com/question/31828911
#SPJ11
Alissa is trying to expand and simplify (p-2)^2
Here is her working
Answers
Answer:
Yes because, we'll technically but then we get yur answer
WILL GIVE BRAINLIEST (PLEASE SHOW WORK)
Evaluate sec (11pi/6) without using technology
Answers

What is the value of x in the equation below? Negative 3 minus (negative 8) minus (negative 2) = x
Answers
Answer:
x = 7
Step-by-step explanation:
Step 1: Write everything out
-3 - (-8) - (-2) = x
Step 2: Switch signs
x = -3 + 8 + 2
Step 3: Combine
x = 10 -3
x = 7
Add the equation u-v/8v + 6u-3v/8v
Answers
Answer:
7u-4v/8
Step-by-step explanation:
u+6u=7u
-v+(-3v)=-v-3v=-4v
7u-4u/8
The amunt of money that college students spend on rent each month is usually between $300 and $600. However, there are a few students who spend $1,300. What measure of spread would be most appropriate to measure the amount of money that college student spend on rent per month? Explain in detail why or why not one of the below measures would be used.
A. Median
B. Range
C. Standard Deviation
D. Inquartile Range
Answers
The range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
To measure the amount of money college students spend on rent per month, the most appropriate measure of spread would be the range. The range is the simplest measure of spread and is calculated by subtracting the lowest value from the highest value in a data set. In this case, the range would be $1,300 - $300 = $1,000.
The median would not be the best choice in this scenario because it only represents the middle value in a data set. It does not take into account extreme values like the $1,300 rent expense.
Standard deviation would not be the most appropriate measure of spread in this case because it calculates the average deviation of each data point from the mean. However, it may not accurately represent the spread when extreme values like the $1,300 rent expense are present.
The interquartile range (IQR) would not be the best choice either because it measures the spread of the middle 50% of the data set. It does not consider extreme values and would not accurately represent the range of rent expenses in this scenario.
In summary, the range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
Know more about Standard deviation here,
https://brainly.com/question/29115611
#SPJ11
What is the range of the function f (x)= 4x -6 when the domain is { -4,-2,0,2,6}?
Answers
Answer:
{-22, -14, -6, 2, 18}
Step-by-step explanation:
f(-4)=4(-4)-6=-22
f(-2)=4(-2)-6=-14
f(0)=4(0)-6=-6
f(2)=4(2)-6=2
f(6)=4(6)-6=18
In my D&D Campaign, there is a tavern called the Topaz Thorn. Inside there are 6 humans, 3 gnomes, 4 dwarves, 5 goblins, and one elfFind the probability that when someone exits the tavern they are either a gnome or a goblin.
Answers
The probability that someone exiting the tavern is either a gnome or a goblin can be found by dividing the number of gnomes and goblins by the total number of individuals in the tavern. In this case, there are 3 gnomes and 5 goblins, so the total number of gnomes and goblins is 3 + 5 = 8. The total number of individuals in the tavern is 6 + 3 + 4 + 5 + 1 = 19. Therefore, the probability is 8/19.
To calculate the probability, we consider the total number of favorable outcomes (gnomes and goblins) and divide it by the total number of possible outcomes (all individuals in the tavern). In this scenario, there are 8 favorable outcomes (3 gnomes and 5 goblins) and 19 possible outcomes (6 humans, 3 gnomes, 4 dwarves, 5 goblins, and 1 elf). By dividing 8 by 19, we find that the probability of someone exiting the tavern being either a gnome or a goblin is approximately 0.421 (rounded to three decimal places).
Learn more about probability here:
brainly.com/question/31828911
#SPJ11
A line passes through the points (5, 7) and
(16,35) in the xy-plane. What is the slope
of the line?
Answers
Answer:
Slope = 2 6/11
Step-by-step explanation:
Formula: \( \frac{y2}{x2} - \frac{y1}{x1} = m\)
m = slope.
Substitute the given points into the formula:
\( \frac{35}{16} - \frac{7}{5} = m\)
Solve:
\( \frac{35}{16} - \frac{7}{5} = \frac{28}{11} = 2 \frac{6}{11} \)
Traci paid $11 to get into a carnival. Each game she played cost $3. Which function can be used to find t, the total amount of money Traci will spend after playing g games?

Answers
Answer: Either A or B because you have to add the amount you have to get the total amount she spent.
Step-by-step explanation:
Find the equation of the line slope =-4 through (-2,9)

Answers
Answer:
y = -4x + 1
Step-by-step explanation:
Okay, one way we can find the equation is to plug the x and y values into y = mx + b
We m (slope) is -4 so
y = -4x + b
We want to find b so we plug in x and y (-2 and 9)
9 = -4 (-2) + b
9 = 8 + b
In this case, b is 1
Now we plug this to make our equation,
y = -4x + 1
Hi there!
The question is asking us to find the equation of the line, given that it has a slope of 4, and it passes through (-2,9).
I will go about solving this by using point-slope:
\(\sf{y-y_1=m(x-x_1)}\)
\(\sf{y-9=-4(x-(-2)}\)
\(\sf{y-9=-4(x+2)}\\\sf{y-9=-4x-8}\\\sf{y=-4x-8+9}\\\sf{y=-4x+1}\)
Therefore, the line's equation is y = -4x + 1.
Have a fantastic day!
need help on this equation

Answers
Answer:
x =1Step-by-step explanation:
Given the following DE = 4X-2
EF = 3x+2
FG 5x-3
GD = 2x+5
Since DE is parallel to GF, this means that the sides are equal hence;
4x - 2 = 5x - 3
4x - 5x = -3 + 2
-x = -1
x = 1
Hence the value of x is 1
HELP ASAP
Given the equation: 2x – 4 = 7, which property should be applied first?
Division Property
Subtraction Property
Multiplication Property
Addition Property
Answers
PLEASE HELP ME OUT I WILL GIVE BRAINLIEST
Perform the following conversions using unit fractoring
4.2 L = _____cm ^3
0.35 km = ______ m
Answers
Answer:
4.2L=4200^3<this one Is a I think
0.35km=350m<This one ik
Step-by-step explanation:
pls help
with this activity
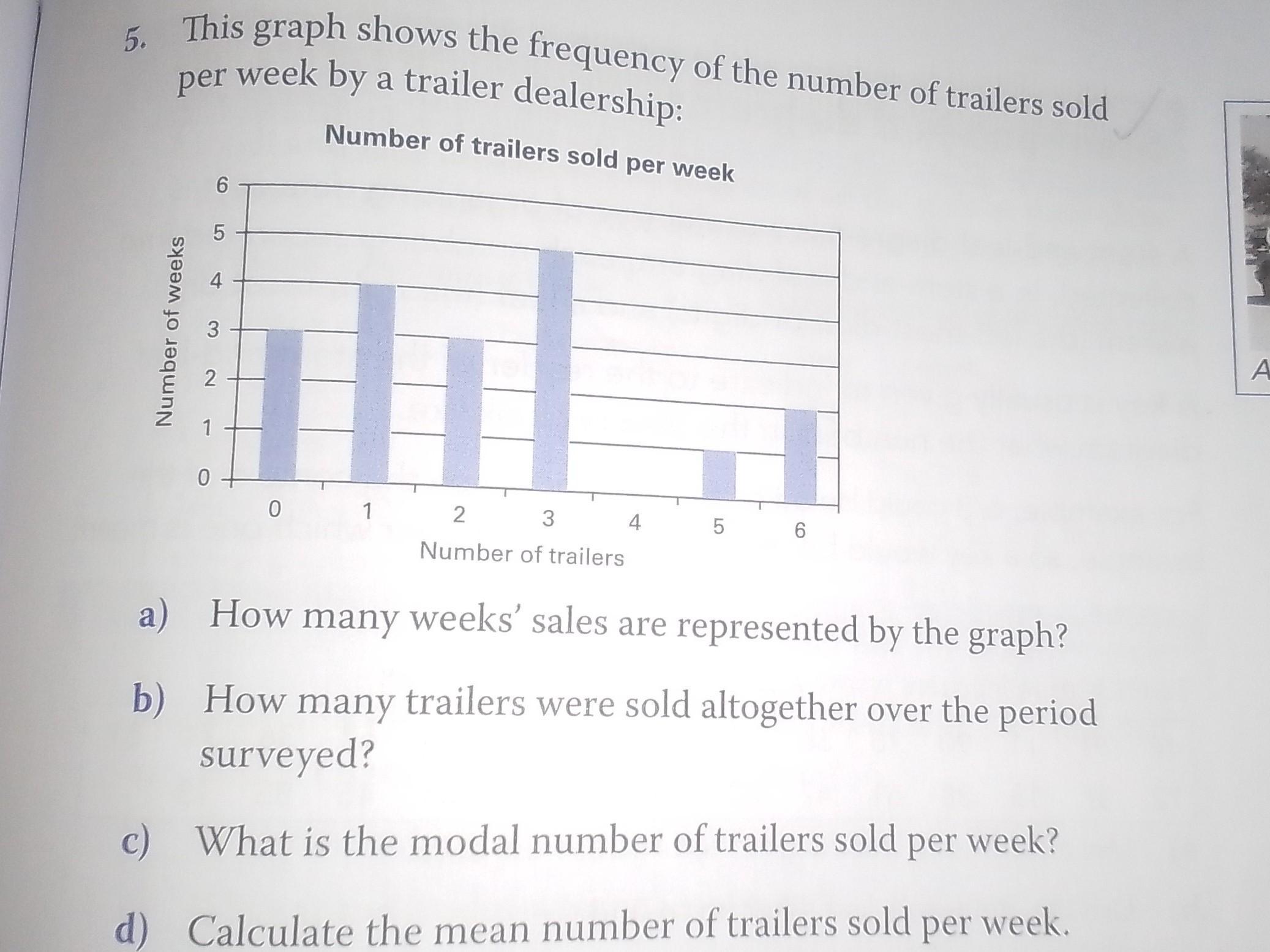
Answers
Answer:
A- 6 weeks
B-18 trailers
C-3 trailers
D- the mean is 3
Step-by-step explanation:
Help me!
Find the area of figure.

Answers
Answer:
9 cm²
Step-by-step explanation:
the area = ½× 3√2 × 3√2 = ½×18 = 9
Find the 16th term of the arithmetic sequence whose common difference is d=6 and whose first term is a 1=3
Answers
Answer:
93
Step-by-step explanation:
This question is on Arithmetic sequence, and we can find the 16th term using the Arithmetic sequence formula below;
aₙ= a₁ + (n-1)d
Where n= nth term in that particular sequence.
n₁= first term in the particular sequence.
d= common sequence between the terms.
Given:
d=6
a₁ =3.
Using the formula above,
a₁₆= 3 + (16-1)6
= 3+(15)6
=3+90
=93
Hence, the the 16th term of the arithmetic sequence is 93
Find the circumference of great circle of sphere whose volume is 36πcm^3
Answers
Answer:
The formula for the volume of a sphere is:
V = (4/3)πr^3
where V is the volume and r is the radius of the sphere.
We are given that the volume of the sphere is 36π cm^3, so we can write:
36π = (4/3)πr^3
Simplifying:
r^3 = (36/4) * 3
r^3 = 27
r = 3
Therefore, the radius of the sphere is 3 cm.
The circumference of a great circle on a sphere is given by the formula:
C = 2πr
where r is the radius of the sphere.
So, the circumference of the great circle is:
C = 2π(3) = 6π
Therefore, the circumference of the great circle of the sphere is 6π cm.
1 3 -27 Let A = 2 5 -3 1-3 2-4 . Find the volume of the parallelepiped whose edges are given by its column vectors with end point at the origin.
Answers
Answer:
The volume of the parallelepiped is 247 cubic units.
Step-by-step explanation:
The volume of the parallelepiped formed by the column vectors of a matrix A is given by the absolute value of the determinant of A. Therefore, we need to compute the determinant of the matrix A:
det(A) = (1)(5)(-4) + (-3)(-3)(-3) + (2)(-3)(2) - (-27)(5)(2) - (3)(-4)(1)(-3)
= -20 - 27 - 12 + 270 + 36
= 247
Since the determinant is positive, the absolute value is the same as the value itself.
To Know more about parallelepiped refer here
https://brainly.com/question/29140066#
#SPJ11
Scores for a common standardized college aptitude test
are normally distributed with a mean of 507 and a
standard deviation of 104. Randomly selected students
are given a Test Preparation Course before taking this
test. Assume, for sake of argument, that the
preparation course has no effect.
If 1 student is randomly selected, find the probability
that their score is at least 555.3.
P(X> 555.3) =

Answers
The probability that their score is at least P(X> 555.3) = 0.8275
What is a normal distribution?
A continuous probability distribution for a real-valued random variable is called a normal distribution or a Gaussian distribution.
Here, we have
Let x denotes the score of a man.
standard deviation (σ) = 104
mean (μ) = 507
If 1 of the men is randomly selected, find the probability that his score is at least 553.5 will be :-
P(X > 553.5) = 1 - P(X ≤ x)
= 1 - P{((x - μ)/σ) ≤ (553.5 - 507/104)}
= 1 - P(z ≤ 0.447)
= 1 - 0.1725
= 0.8275
Hence, the probability that their score is at least P(X> 555.3) = 0.8275
To learn more about the normal distribution from the given link
https://brainly.com/question/4079902
#SPJ1
For his long distance phone service, tony pays $3 monthly fees plus 11 cents per minute. Last month, Tony's long distance bill was $22.03. For how many minutes was tony billed
Answers
Answer:
11+11= 22 answer is $ 22.03
The mean SAT score in mathematics is 538. The standard deviation of these scores is 35. A special preparation course claims that the mean SAT score, u, of its graduates is greater than 538. An independent researcher tests this by taking a random sample of 80 students who completed the course; the mean SAT score in mathematics for the sample was 542. At the 0.01 level of significance, can we conclude that the population mean SAT score for graduates of the course is greater than 538?
Answers
At 0.01 level of significance, we cannot conclude that the population mean SAT score for graduates of the course is greater than 538.
To determine if we can conclude that the population mean SAT score for graduates of the course is greater than 538, we can conduct a one-sample t-test.
Provided information:
- Sample size (n) = 80
- Sample mean (xbar) = 542
- Population mean (μ) = 538
- Standard deviation (σ) = 35
- Significance level (α) = 0.01
The null hypothesis (H₀) assumes that the population mean SAT score for graduates of the course is equal to or less than 538:
H₀: μ ≤ 538
The alternative hypothesis (H₁) assumes that the population mean SAT score for graduates of the course is greater than 538:
H₁: μ > 538
We'll calculate the test statistic and compare it to the critical value to make our conclusion.
First, calculate the standard error of the mean (SEM):
SEM = σ / √n
SEM = 35 / √80
SEM ≈ 3.92
Next, calculate the t-value:
t = (xbar - μ) / SEM
t = (542 - 538) / 3.92
t ≈ 1.02
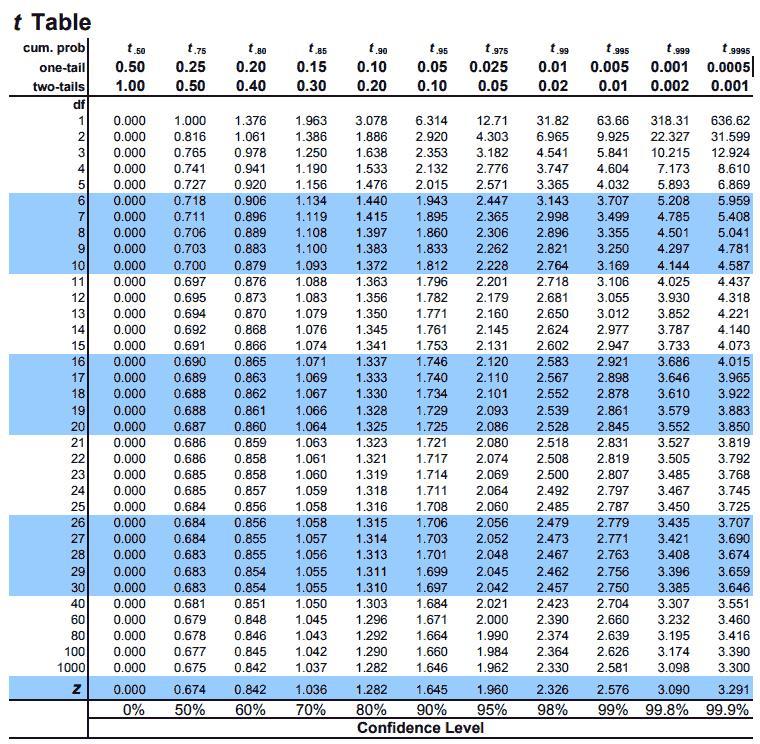
Now, we need to determine the critical value. Since the alternative hypothesis is one-tailed (greater than), we'll use the upper critical value for a t-distribution at the provided significance level.
Looking up the critical value in a t-table or using a statistical software, at α = 0.01 with 79 degrees of freedom (n - 1), we obtain the critical value to be approximately 2.623.
Since the calculated t-value (1.02) is less than the critical value (2.623), we fail to reject the null hypothesis.
Therefore, based on the provided information, we cannot conclude that the special preparation course significantly improves the population mean SAT score.
To know more about level of significance refer here:
https://brainly.com/question/31519103#
#SPJ11
Help on a homework assignment

Answers
1. Definition of Congruence:∠ RSU ≅ ∠ VST
2. Definition of Congruence: m∠ RSU = m∠ VST
3. Angle Addition Postulate: m∠ RSU + m∠ USV = m/RSV
4. Angle Addition Postulate: m∠ VST + m∠ USV = m∠ UST
5. Transitive Property: m∠ RSU + m∠ USV = m∠ UST
6. Substitution Property: m∠ RSV = m∠ UST
7. Definition of Congruence: ∠ RSV ≅ ∠ UST
What is the transitive property?In mathematics, a relation R on a set X is said to have a transitive property if, for all elements a, b, c in X, whenever R relates a to b and b to c, then R also relates a to c.
This is shown in the case of number 6 where :
m∠ RSU + m∠ USV = m∠ UST
The transitive property is also shown in equality states where all values of a, b, and c, if a = b, and b = c, then a = c.
Learn more about the transitive property at: https://brainly.com/question/2437149
#SPJ1
An online video game has five servers. For each server, the probability of it working on a given day is 0. 9. The game developers decided that if two or fewer servers are working, the game will shut down, otherwise, it will continue. It is reasonable to assume that the servers are independent of each other. Given that the game is not shut down, what is the probability that all 5 servers are working?
In the answer sheet it says the probability is 1/(n-1) * ∑(x(i)-x(bar)), but I don't understand that and it doesn't actually give the answer, just this formula. So what is the answer and how do I come up with it?
Answers
The probability that all 5 servers are working, given that the game is not shut down, is 0.59049 or approximately 0.59.
To find the probability that all 5 servers are working, given that the game is not shut down, we need to use conditional probability. We know that if two or fewer servers are working, the game will shut down. Therefore, we are interested in finding the probability that more than two servers are working.
Since the servers are assumed to be independent, the probability that a single server is working is 0.9, and the probability that it is not working is 1 - 0.9 = 0.1.
To find the probability that more than two servers are working, we can calculate the complement of the event "two or fewer servers working." The complement is the event "three or more servers working." We can calculate this probability using the binomial probability formula:
\(P(X \geq k) = 1 - P(X < k)\)
In this case, k = 3 (since we want three or more servers working), n = 5 (total number of servers), and p = 0.9 (probability of a server working).
Using the formula, we get:
\(P(X \geq3) = 1 - P(X < 3)\\ = 1 - P(X = 0) - P(X = 1) - P(X = 2)\\ = 1 - (0.1^5) - (5 * 0.1^4 * 0.9) - (10 * 0.1^3 * 0.9^2)\\ \approx 0.59049\\\)
Therefore, the probability that all 5 servers are working, given that the game is not shut down, is approximately 0.59049 or 59%.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
The radius of a large balloon is increasing at a rate of 2 inches per second. How fast, in cubic inches per second, is the volume increasing when the radius is 10 inches
Answers
The volume of the balloon is increasing at a rate of 800π cubic inches per second when the radius is 10 inches.
Using the volume of a sphere formula, V = (4/3)πr³, where V is the volume and r is the radius, we can determine how quickly the balloon's volume is growing.
We are given that the radius is increasing at a rate of 2 inches per second, so dr/dt = 2.
We need to find dV/dt, the rate at which the volume is changing with respect to time. To do this, we can differentiate the volume formula with respect to time using the chain rule:
dV/dt = dV/dr × dr/dt
First, let's find dV/dr. Differentiating the volume formula with respect to the radius gives us:
dV/dr = d/dt ((4/3)πr³) = 4πr²
We can now enter the supplied values into the equation as follows:
dV/dt = (4πr²) × (dr/dt) = (4π(10)²) × (2)
Calculating this expression gives us the rate of change of the volume:
dV/dt = 800π cubic inches per second
So, when the radius is 10 inches, the volume of the balloon is increasing at a rate of 800π cubic inches per second.
Learn more about the volume at
https://brainly.com/question/30762915
Two isosceles triangles are shown below. If 180 - z = 2y and y = 69, what is the value of x ?
Answers
Answer:
x = 69
Step-by-step explanation:
Knowns:
y = 69
Problem Workout
180 - z = 2y
180 - z = 2 (69)
180 - z = 138
-z = -42
z = 42
Since there is no picture, I am guessing x is the third angle.
x = 180 - (y + z)
x = 180 - (69 + 42)
x = 180 - 111
x = 69