Last week's discussion involved development of a multiple regression model that used miles per gallon as a response variable. Weight and horsepower were predictor variables. You performed an overall F-test to evaluate the significance of your model. This week, you will evaluate the significance of individual predictors. You will use output of Python script from Module Six to perform individual t-tests for each predictor variable. Specifically, you will look at Step 5 of the Python script to answer all questions in the discussion this week.
In your initial post, address the following items:
What is the slope coefficient for the weight variable? Is this coefficient significant at 5% level of significance (alpha=0.05)? (Hint: Check the P-value, , for weight in Python output. Recall that this is the individual t-test for the beta parameter.) See Step 5 in the Python script.
What is the slope coefficient for the horsepower variable? Is this coefficient significant at 5% level of significance (alpha=0.05)? (Hint: Check the P-value, , for weight in Python output. Recall that this is the individual t-test for the beta parameter.) See Step 5 in the Python script.
Last week, you performed an overall F-test. Why do you now need to perform individual t-tests? What are the differences in the interpretation of the two tests?
What is the coefficient of determination of your multiple regression model from Module Six? Provide appropriate interpretation of this statistic.
Below is step 5. There are no missing information. The python script is from step 5. This is the information needed to solve the questions thank you
This is step 5 OLS Regression Results
==============================================================================
Dep. Variable: mpg R-squared: 0.822
Model: OLS Adj. R-squared: 0.808
Method: Least Squares F-statistic: 62.13
Date: Fri, 14 Feb 2020 Prob (F-statistic): 7.88e-11
Time: 05:00:39 Log-Likelihood: -69.730
No. Observations: 30 AIC: 145.5
Df Residuals: 27 BIC: 149.7
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 37.8867 1.748 21.674 0.000 34.300 41.473
wt -4.0629 0.694 -5.855 0.000 -5.487 -2.639
hp -0.0318 0.009 -3.470 0.002 -0.051 -0.013
==============================================================================
Omnibus: 5.277 Durbin-Watson: 1.919
Prob(Omnibus): 0.071 Jarque-Bera (JB): 3.980
Skew: 0.878 Prob(JB): 0.137
Kurtosis: 3.314 Cond. No. 620.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Answers
The slope coefficient for the weight variable is -4.0629, and it is significant at the 5% level of significance (alpha=0.05).
The slope coefficient for the horsepower variable is -0.0318, and it is also significant at the 5% level of significance (alpha=0.05).
The individual t-tests are conducted to determine the significance of each predictor variable separately, assessing their contribution to the model, while the overall F-test performed last week evaluated the significance of the model as a whole in explaining the variation in the response variable.
The coefficient of determination (R-squared) for the multiple regression model is 0.822, indicating that approximately 82.2% of the variability in the response variable (mpg) can be explained by the predictor variables (weight and horsepower).
To answer the questions based on the given Python script output:
The slope coefficient for the weight variable is -4.0629.
According to the Python output, the P-value for weight is 0.000. Since the P-value is less than the significance level of 0.05, we can conclude that the coefficient for weight is significant at the 5% level of significance.
The slope coefficient for the horsepower variable is -0.0318. The P-value for horsepower is given as 0.002 in the Python output.
Similar to the previous case, since the P-value is less than 0.05, the coefficient for horsepower is also significant at the 5% level of significance.
Although an overall F-test was performed last week to evaluate the significance of the model, individual t-tests are needed now to determine the significance of each predictor variable.
The overall F-test assesses whether there is a significant linear relationship between the predictors and the response variable as a whole.
In contrast, the individual t-tests examine the significance of each predictor variable separately, providing insights into their individual contributions to the model.
The coefficient of determination (R-squared) for the multiple regression model is 0.822.
This statistic represents the proportion of the variance in the response variable (mpg) that can be explained by the predictor variables (weight and horsepower).
In this case, approximately 82.2% of the variability in mpg can be accounted for by weight and horsepower.
For similar question on slope coefficient.
https://brainly.com/question/30355310
#SPJ11
Related Questions
Use long division to find the quotient below.
(2x3 + x2 + 25) /(2x+5)
Answers
Answer:
x^2 -2x +5
Step-by-step explanation:
x^2 -2x +5
----------------------------------------------------------
2x + 5 / 2x^3 + x^2 + 0x + 25
-(2x^3 + 5x^2)
----------------------------
-4x^2 + 0x
-( -4x^2 - 10x )
-----------------------------------------
10x + 25
-(10x + 25)
---------------------------
0
The desired quotient is x^2 -2x +5
WHat is the best method for this system?

Answers
Answer:
Elimination method
Step-by-step explanation:
We have a choice to eliminate the y or x:
I chose x
So now we double the second equation to make the co efficient of x the same:
6x-5y = -3
6x+4y = 24
Now we subtract both equations to eliminate the x's:
6x-5y = -3
- - -
6x+4y = 24
-9y = -27
y = 3
Now we substitute this value into either equation 1 or 2:
I chose 2
3x + 2(3) =12
Simplify:
3x + 6 =12
Subtract 6 from both sides:
3x + 6 -6 = 12 -6
Simplify:
3x = 6
Divide both sides by 3:
3x÷3 = 6÷3
Simplify:
x = 2
Answer:
(2, 3 ) by the elimination method
Step-by-step explanation:
6x - 5y = - 3 → (1)
3x + 2y = 12 → (2)
multiplying (2) by - 2 and adding to (1) will eliminate x
- 6x - 4y = - 24 → (3)
add (1) and (3) term by term to eliminate x
0 - 9y = - 27
- 9y = - 27 ( divide both sides by - 9 )
y = 3
substitute y = 3 into either of the 2 equations and solve for x
substituting into (2)
3x + 2(3) = 12
3x + 6 = 12 ( subtract 6 from both sides )
3x = 6 ( divide both sides by 3 )
x = 2
solution is (2, 3 )
The graph of a figure is shown below.
Which graph represents the reflection of this figure across the x-axis?
the first triangle in the photo
which is reflected on the x-axis





Answers
A graph which represents the reflection of this figure across the x-axis is: graph 5.
What is a reflection across the x-axis?In Mathematics, a reflection across the x-axis would maintain the same x-coordinate while the sign of the y-coordinate changes from positive to negative. Therefore, a reflection across the x-axis is given by this transformation rule:
(x, y) → (x, -y) = (3, 1) → (3, -1).
(x, y) → (x, -y) = (4, 0) → (4, 0).
(x, y) → (x, -y) = (3, -1) → (3, 1).
(x, y) → (x, -y) = (4, -2) → (4, 2).
(x, y) → (x, -y) = (2, -4) → (2, 4).
(x, y) → (x, -y) = (0, -2) → (0, 2).
In conclusion, a reflection across the x-axis would transform the geometric figure to that shown in the graph attached in the image below.
Read more on reflection here: brainly.com/question/20602330
#SPJ1

The base of a parallelogram is six more than twice the height. The height is 5 inches. What is the length of the base?
Answers
The length of the base of the parallelogram is 16 inches.
What is parallelogram?
A parallelogram is a four-sided plane figure with opposite sides parallel and congruent (having the same length). This means that the opposite sides of a parallelogram are parallel to each other and have the same length. Additionally, the opposite angles of a parallelogram are equal in measure, which means they have the same degree of rotation.
Let's use the information given in the problem to set up an equation and solve for the length of the base.
From the problem, we know that the height of the parallelogram is 5 inches.
h = 5
We also know that the base of the parallelogram is six more than twice the height. Let's use b to represent the length of the base:
b = 2h + 6
Now we can substitute the value we know for the height and solve for the base:
b = 2(5) + 6
b = 10 + 6
b = 16
Therefore, the length of the base of the parallelogram is 16 inches.
To learn more about parallelogram visit the link:
https://brainly.com/question/970600
#SPJ1
Compare / Contrast Exponential Equations
1.) 2 (1/5)x-5
2.) y=4x
Answers
The functions y = 2 (1/5)^x - 5 and y = 4^x are compared as follows
y = 2 (1/5)^x - 5 y = 4^x
Initial value: 2 1
base function: 1/5 = decay function 4 = growth function
Translation: 5 units down no transformation
What is a decay function?
A decay function is a mathematical function used in various fields such as physics, engineering, economics, and machine learning, to model the reduction or decline of a value over time.
It is a type of function that decreases at a rate proportional to its current value, so that it approaches zero as time progresses.
Decay function are exponential functions with the base function as
0 < k < 1This is the opposite of growth function which has values greater than 1
Learn more about growth functions at:
https://brainly.com/question/27161222
#SPJ1
Graph the equation by plotting three
points. If all three are correct, the line
will appear.
-3y = -x - 7
Answers
Answer:
spam question
not able to answer
Step-by-step explanatio
mark me
an experiment can be assumed to have internal validity if multiple choice all variables other than the independent variable are kept constant. the dependent variable is valid. confounding variables are present. there is a strong manipulation of the independent variable.
Answers
An experiment can be assumed to have internal validity if random assignment and experimental control is employed. So the option c is correct.
The degree to which a study reliably establishes a cause-and-effect link is a sign of its internal validity. The procedures used in the study and the level of care done have a significant impact on this type of validity.
Internal validity is essential because, if proven, it enables alternate explanations for a discovery to be disregarded.
An experiment can be assumed to have internal validity if random assignment and experimental control is employed. So the option c is correct.
To learn more about experiment link is here
brainly.com/question/11256472
#SPJ4
The right question is:
An experiment can be assumed to have internal validity if:
A. the dependent variable is valid.
B. there is a strong manipulation of the independent variable.
C. random assignment and experimental control is employed.
D. confounding variables are present.
La razón geométrica de dos números es 13/6 y su diferencia es 35 ¿Cuál es el número mayor?
En una fiesta la relación de hombre a mujeres es de 9 a 7. Si se cuentan 45 hombres ¿Cuántas mujeres hay?
Un traje para hombre costó $ 250. 000 el año pasado. Este año la docena de dichos trajes cuesta $ 3’250. 000 ¿cuál es la razón geométrica del precio antiguo y actual del traje?
Answers
The greater number is 455.
There are 197 women in the party.
The geometric ratio of the old and current price of the suit is 25/27.
The first problem requires the application of geometric ratios and algebraic manipulation to determine the greater of the two numbers. Geometric ratios are ratios between two quantities that are constant throughout.
We are also given that their difference is 35, which can be expressed as x - y = 35. We can use algebraic manipulation to solve for the values of x and y.
From the first equation, we can express x in terms of y as x = (13/6)y. Substituting this value of x into the second equation, we get (13/6)y - y = 35. Simplifying this equation, we get y = 210.
To find the value of x, we can substitute y = 210 into the equation x/y = 13/6, giving us x = 455. Therefore, the greater number is 455.
The second problem involves using ratios to find the number of women in a party. We are given that the ratio of men to women is 9 to 7, which can be expressed as 9x/7x, where x is a constant. We are also told that there are 45 men. We can use this information to solve for the number of women.
Therefore, the total number of parts is 45/9 = 5.
We can use this information to find the number of women, which is 7 parts of the ratio, or
=> 7x = (7/16) * 5 * 45 = 196.875.
Since we cannot have a fraction of a person, we round this value up to the nearest whole number, which is 197.
Therefore, there are 197 women in the party.
The third problem involves finding the geometric ratio of the old and current price of a men's suit. We are given that the suit cost $250,000 last year and that a dozen of these suits cost $3,250,000 this year. We can use the information provided to find the geometric ratio.
Since a dozen of the suits cost $3,250,000, one suit costs $3,250,000/12 = $270,833.33. The ratio of the old price to the new price is 250,000/270,833.33, which simplifies to 25/27.
Therefore, the geometric ratio of the old and current price of the suit is (25/27)¹ = 25/27.
To know ore about geometric ratio here
https://brainly.com/question/29067806
#SPJ4
Complete Question:
The geometric ratio of two numbers is 13/6 and their difference is 35. What is the greater number?
At a party the ratio of men to women is 9 to 7. If 45 men are counted, how many women are there?
A men's suit cost $250,000 last year. This year a dozen of these suits cost $3,250. 000 What is the geometric ratio of the old and current price of the suit?
If 3+x<5 and 8+x>5,What range of values of x satisfies both inequalities?
Answers
The range of values of x which satisifies both of the inequalities is:
(-3, 2)
What range of values of x satisfies both inequalities?Here we have two inequalities:
3 + x < 5
8 + x > 5
And we want to see which range of values of x satisfie both of these inequalities.
If we isolate x on both inequalities, we will get:
3 + x < 5
x < 5 - 3
x < 2
And the other one is:
8 + x > 5
x > 5 - 8
x > -3
Then we havethe compound inequality:
x < 2
x > -3
Then the range of values that satisfies both inequalities is (-3, 2)
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
3.5−2.46=1.16
Describe Maysa's error. Explain how you would use a model or place-value concepts to help Maysa build understanding. Give the correct answer in your explanation.
Answers
The correct answer for the given subtraction is:
3.5 - 2.46 = 1.04
How to solve the subtraction?
Here we want to find the subtraction between two numbers in decimal form:
3.5 - 2.46 = 1.16
Now, this is clearly wrong, as 0.46 is smaller than 0.5, so the decimals after the decimal point are incorrect, now let's solve it again.
First, we can rewrite these two numbers as:
3.5 = 3 + 0.5
2.46 = 2 + 0.46
Then the subtraction can be rewritten as:
3.5 - 2.46
(3 + 0.5) - (2 + 0.46)
Now we group like terms:
(3 - 2) + (0.5 - 0.46)
1 + (0.50 - 0.46)
1 + (0.04)
Now we group that, so we get:
1 + (0.04) = 1.04
This is the correct answer to the given subtraction.
If you want to learn more about subtractions:
https://brainly.com/question/25421984
#SPJ1
The height of a ball thrown straight up from the ground with a velocity of 96ft/s is given by the quadratic function h(t)=-16 t²+96 t . What is the maximum height the ball reaches?
(a) 6ft (b) 128ft (c) 144ft (d) 160ft
Answers
The correct option is (c) 144ft
The maximum height the ball reaches is 144ft.
What is quadratic function ?A quadratic function has the form of equation as ax²+ bx + c, where a, b, and c are the numbers not equal to zero. In mathematics, the quadratic function, the quadratic polynomials , 2 degree polynomial is a polynomial function with one or more that one variables in which the highest term is of the second degree.
In the question,
h(t)=-16 t²+96 t
and velocity = 96ft/s
out the -16 from the equation.
h(t)= -16 ( t² + 6 t )
h(t) = −16(t² −6t+9−9)
= −16(t² −6t+9)+144
Factor the equation to get a perfect square ,t = 3 then h(t) = 144. The maximum height is 144.
−16(t−3)² +144
Thus, height is 144 ft.
To know more about quadratic functions, visit :
https://brainly.com/question/5975436
#SPJ4
Which ordered pair is a solution to the equation? -7x+3y=2
Answers
Answer:
(-7, 3) i think, not 100% sure
Step-by-step explanation:
Answer:
Both (1,3) and (-2,-4)
Step-by-step explanation: i got it right in Khan Academy (n˘v˘•)¬
hope it helps!
if a town with a population of 500 doubles in size ever 9 years, what will the population be 36 years from now?
Answers
The population of the town in 36 years would be 8000.
What would be the population of the town in 36 years?The formula that can be used to determine the town's population is:
FV = P (1 + r)^n
Where:
FV = Future value P = Present value R = rate of growth = 100%N = number of years = 36/9 = 4500 x 2^4 = 8000
To learn more about future value, please check: https://brainly.com/question/18760477
which term best represents the intersection of two pages of an open book? line startfragment, line, angle startfragment, angle, point startfragment, point, plane
Answers
The term that best represents the intersection of two pages of an open book is point.
What is intersection?A third item made up of everything that is simultaneously contained in all of the other things is called an intersection of two or more objects in mathematics. In Euclidean geometry, for instance, the intersection of two lines in a plane that are not parallel is where they come together. More broadly, the set of elements that are a part of all of the sets is what is meant by the intersection of sets in set theory. The items being considered do not need to be in a shared space, unlike the Euclidean concept.
A point is the most frequent shape for an intersection in plane geometry, while there are other shapes that can be used as well. An intersection is an item of lesser dimension that is incident to each in incidence geometry, which is typically applied to flats.
To learn more about intersection ,visit:
https://brainly.com/question/12089275
#SPJ4
I need help I’m stuck

Answers
Answer:
Step-by-step explanation:
A laundry basket has 24 t-shirts in it. Four are navy, twelve are red and the remaining are white. What is the probability of not selecting a red shirt? *
Answers
Answer:
50%
Step-by-step explanation:
Identify the population of shirts that are *NOT red.* In this case 12 are red. This means that 12 shirts are *not red.* 12/24 = .5 or 50% probability.
U7L2 Cool Down
The measure of the arc from B to A not passing through C is 26 degrees.
1. What is the measure of angle BOA ?
2. What is the measure of angle BDA?
3. What is the measure of angle BCA ?
degrees
degrees
degrees
Answers
Using the inscribed angle theorems, the measure of the indicated angles are:
1. m∠BOA = 26°
2. m∠BDA = 13°
3. m∠BCA = 13°
What is the Inscribed Angle Theorems?Based on the inscribed angle theorem, the following relationships are established:
Inscribed angle = 2(measure of intersected arc)Central angle = measure of intersected arcGiven:
Intercepted arc BA = 26°
1. ∠BOA is central angle
Thus:
m∠BOA = 26° (inscribed angle theorems)
2. ∠BDA is inscribed angle.
m∠BDA = 1/2(30) = 13° (inscribed angle theorems)
3. m∠BCA = m∠BDA = 13° (inscribed angle theorems)
Learn more about inscribed angle theorems on:
https://brainly.com/question/30494878
Triangle ABC is shown below. What is the measure of angle??

Answers
Then do 180-118=62
25 points plus brainliest
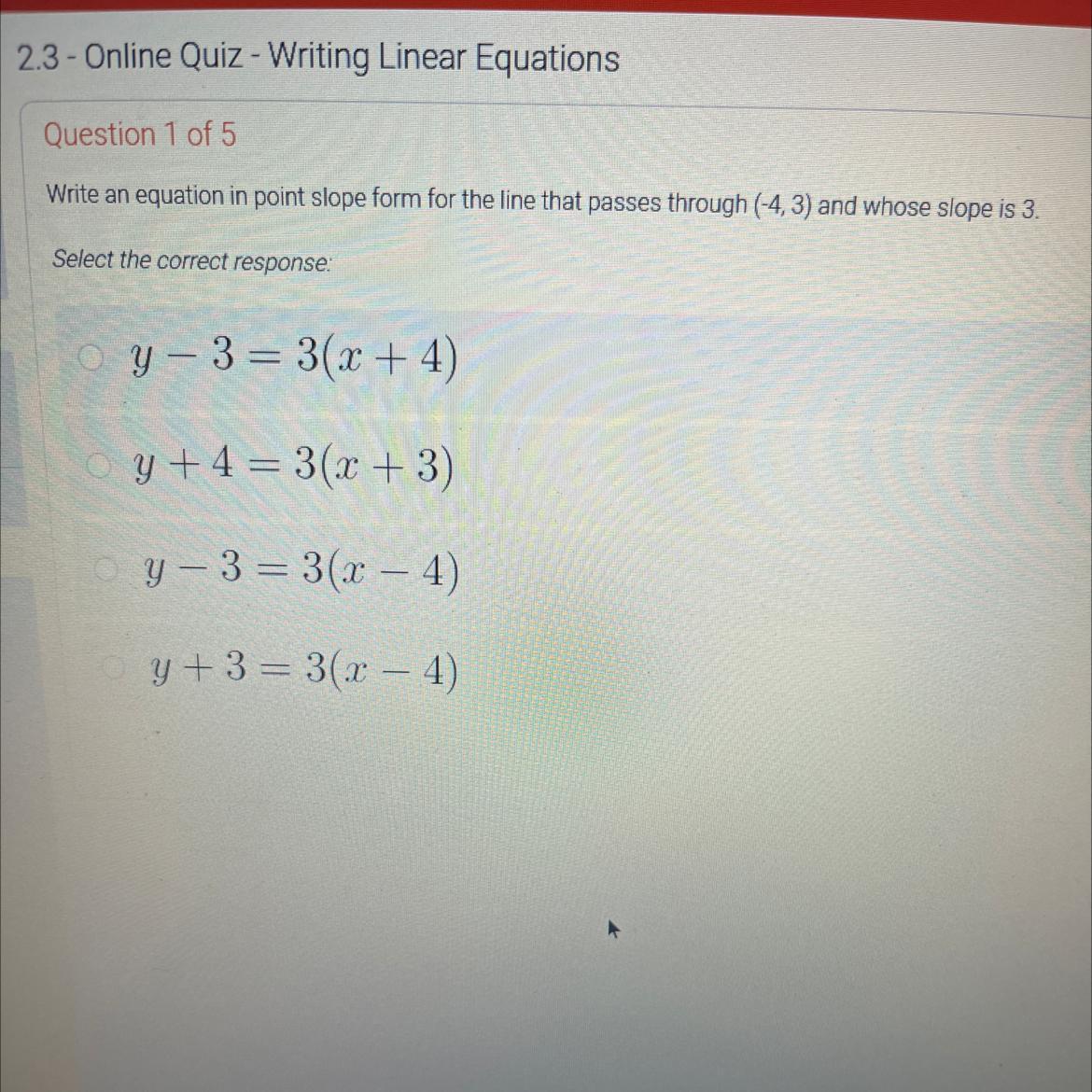
Answers
Answer: y-3 = 3(x+4)
Step-by-step explanation:
See attached

is 30 a rational number?
Answers
Answer: Yes
Step-by-step explanation:
It is in all the rational number categories like natural, whole, integer, or just rational numbers.
find the derivative of the function g(x) = (x^2 - x +
1)^10.(tanx)^3.
Answers
The derivative of the function g(x) = (x² - x + 1\()^1^0\) * (tan(x))³ is g'(x) = 10(x² - x + 1)⁹ * (2x - 1) * (tan(x))³ + 3(x² - x + 1\()^1^0\) * (tan(x))² * sec²(x).
To find the derivative of the given function g(x), we can apply the product rule and the chain rule. Let's break down the function into its constituent parts: f(x) = (x² - x + 1\()^1^0\) and h(x) = (tan(x))³.
Using the product rule, the derivative of g(x) can be calculated as g'(x) = f'(x) * h(x) + f(x) * h'(x).
First, let's find f'(x). We have f(x) = (x² - x + 1\()^1^0\), which is a composite function. Applying the chain rule, f'(x) = 10(x² - x + 1\()^9\) * (2x - 1).
Next, let's determine h'(x). We have h(x) = (tan(x))³. Applying the chain rule, h'(x) = 3(tan(x))² * sec²(x).
Now, we substitute these derivatives back into the product rule formula:
g'(x) = f'(x) * h(x) + f(x) * h'(x)
= 10(x² - x + 1)² * (2x - 1) * (tan(x))³ + 3(x² - x + 1\()^1^0\)* (tan(x))² * sec²(x).
In summary, the derivative of the function g(x) = (x² - x + 1\()^1^0\) * (tan(x))³ is g'(x) = 10(x² - x + 1)⁹ * (2x - 1) * (tan(x))³ + 3(x² - x + 1\()^1^0\) * (tan(x))² * sec²(x).
Learn more about derivative
brainly.com/question/29144258
#SPJ11:
Use variation of parameters to solve the given initial-value problem. X′=(3−1−13)X+(4e2t4e4t),X(0)=(11) The answer must be in system of linear first differential equation
Answers
The solution to the given initial-value problem is X(t) = [e^t(3e^3t + 7) - e^(4t)(e^3t - 1)]/5.
To solve the given initial-value problem using the variation of parameters method, we first need to find the general solution to the homogeneous equation. The homogeneous equation is X' = (3 - 1/e)X.
By solving this homogeneous equation, we find that the general solution to the homogeneous equation is X_h(t) = Ce^t + De^(3t), where C and D are constants.
Next, we need to find the particular solution X_p(t) that satisfies the given non-homogeneous term. By assuming X_p(t) = u(t)e^t, we can determine the variation of parameters u(t).
Substituting X_p(t) = u(t)e^t into the original equation, we obtain u'(t)e^t = (4e^2t)/(5e^t). Simplifying this equation, we find u'(t) = 4/5e^t.
By integrating both sides, we get u(t) = (4/5)e^t + C, where C is the constant of integration.
Therefore, the particular solution is X_p(t) = [(4/5)e^t + C]e^t = (4/5)e^2t + Ce^t.
Combining the homogeneous and particular solutions, we have X(t) = X_h(t) + X_p(t) = Ce^t + De^(3t) + (4/5)e^2t + Ce^t.
Using the initial condition X(0) = (1/1), we can solve for the constants C and D. After solving, we obtain the solution X(t) = [e^t(3e^3t + 7) - e^(4t)(e^3t - 1)]/5.
To learn more about homogeneous equation click here
brainly.com/question/32592901
#SPJ11
Explain why∣2x+5∣=−7 has no solutions.
Answers
Absolute value represents how far you are from zero on the number line.
Examples:
-27 is 27 units from zero, so |-27| = 2734 is 34 units from zero, so |34| = 34The output of an absolute value function is never negative. Negative distance does not make sense. Therefore, we have no way to reach an output of -7. This is why we have no solutions here.
3/4 divided by 1/3 as a fraction
Answers
Answer:
\(\frac{9}{4}\)
Step-by-step explanation:
Answer:
\(\frac{9}{4}\)
Step-by-step explanation:
\(\frac{3}{4}\) ÷ \(\frac{1}{3}\)
\(\frac{3}{4}\) × \(\frac{3}{1}\) = \(\frac{9}{4}\) ( to divide we make the other fraction reciprocal)
\(\frac{9}{4}\) as mixed fraction= \(\frac{1}{4}{2}\)
The ratio of the number of men to the number of
women working at Forms, Inc. is 7:2. Altogether there
are 360 workers at the company. How many of the
workers are women?
Answers
Answer:
280 men; 80 women.
Step-by-step explanation:
this task can be solved used system of two equation (note, it is not the only and shortest way):
1) if number of men is 'm', women is 'w' and ratio is 7:2, then it is possible to write the first equation: m/w=7/2;
if together there are 360, then it is possible to write the second equation of the system: m+w=360.
2) after item 1 it is possible to make up and solve the system:
\(\left \{ {{m/w=7/2} \atop {m+w=360}} \right. \ => \ \left \{ {{7w=2m} \atop {m+w=360}} \right. \ => \ \left \{ {{m=280} \atop {w=80}} \right.\)
a set of five numbers has a mode of 24 a median of 21 a mean of 20 . work out what the numbers could be
Answers
Answer:
Step-by-step explanation:
The mode is 24 so we know that at least 2 of the 5 numbers are 24.
The mean is 20 so we know that the 5 numbers add up to 100.
The median is 21 so the third number is 21.
100-(24+24+21)= 31
Now, I am pretty certain that the last 2 numbers can be anything as long as they add up to 31 AND they are not also 21 because 24 then would no longer be the mode.
E.g. 24, 24, 21, 11 & 20
A grocery store purchases cantaloupes from two warehouses, A and B. The
distribution of the diameters from Warehouse A is approximately normal with a
mean of 120 mm and standard deviation of 6 mm.
(a) For a cantaloupe selected at random from Warehouse A, what is the
probability that the cantaloupe will have a diameter greater than 127 mm?
A randomly selected cantaloupe from Warehouse B has the probability of 0.763
that it will have a diameter greater than 127 mm. The grocery store purchases
40% of their cantaloupes from Warehouse B.
(b) For a cantaloupe selected at random from the grocery store, what is the
probability that the cantaloupe will have a diameter greater than 127 mm?
(c) If the randomly selected cantaloupe's diameter is greater than 127 mm, what
is the probability the cantaloupe came from Warehouse B?
Answers
distribution of the diameters from Warehouse A is approximately normal with a
mean of 120 mm and standard deviation of 6 mm.
(a) For a cantaloupe selected at random from Warehouse A, what is the
probability that the cantaloupe will have a diameter greater than 127 mm?
A randomly selected cantaloupe from Warehouse B has the probability of 0.763
that it will have a diameter greater than 127 mm. The grocery store purchases
40% of their cantaloupes from Warehouse B.
(b) For a cantaloupe selected at random from the grocery store, what is the
probability that the cantaloupe will have a diameter greater than 127 mm?
(c) If the randomly selected cantaloupe's diameter is greater than 127 mm, what
is the probability the cantaloupe came from Warehouse B?
A: The probability of cantaloupe having dia. more than 127 is 0.12167.
B: Cantaloupe selected at random from the warehouse, then the probability that has a diameter of more than 127 mm is 0.3782.
C: The probability that the cantaloupe will be from warehouse B given randomly selected cantaloupe's diameter is greater than 127 mm, is 0.8069.
What is probability?The probability formula is defined as the possibility of an event happening being equal to the ratio of the number of favorable outcomes and the total number of outcomes. Probability is a measure of the likelihood of an event occurring. Also, the favorable number of outcomes cannot be negative.
Given two warehouses, A and B
mean for warehouse A = μ = 120 mm
The standard deviation for warehouse A = σ = 6mm
A: a cantaloupe selected at random from Warehouse A
to find the probability of cantaloupe having a diameter greater than 127 mm = P(x > 127)
P(x > 127) = 1 - P(x ≤ 127)
P(x ≤ 127) = P((x - μ)/σ)
P(x ≤ 127) = P((127 - 120)/6)
P(x ≤ 127) = P(z ≤ 1.66)
P(x ≤ 127) = 0.87833
P(x > 127) = 1 - P(x ≤ 127)
P(x > 127) = 1 - P(x < 127) = 0.12167
probability of cantaloupe having dia. more than 127 is 0.12167.
B: Let event A for distributor A and let event B for distributor B
and event C for a diameter greater than 127 mm.
and given A randomly selected cantaloupe from Warehouse B has a probability of 0.763 that it will have a diameter greater than 127 mm,
and the percentage of cantaloupe provided by B is 40%
rest 60% for A,
therefore, for cantaloupe selected at random, the probability of having a diameter greater than 127 mm is
P(C) = P(C|A)P(A) + P(C|B)P(B)
= 0.12167(0.6) + 0.763(0.4)
= 0.073 + 0.3052
P(C) = 0.3782
cantaloupe selected at random from the warehouse, then the probability that has a diameter of more than 127 mm is 0.3782.
C: the probability the cantaloupe came from Warehouse B, given that the randomly selected cantaloupe's diameter is greater than 127 mm,
P(B|C) = P(B ∩ C)/P(C)
P(B|C) = (P(C|B)P(B))/P(C)
substitute values
P(B|C) = ((0.763)(0.4))/0.3782
P(B|C) = 0.3052/0.3782
P(B|C) = 0.8069
The probability that the cantaloupe will be from warehouse B given randomly selected cantaloupe's diameter is greater than 127 mm, is 0.8069.
Hence the probabilities are,
A; 0.12167
B; 0.3782
C; 0.8069.
Learn more about probability;
brainly.com/question/30034780
#SPJ2
Someone with quick geometry skills, please help!! I need this answer fast!! Thank you!

Answers
Answer:
m∠SPQ = (9x + 7)°
Step-by-step explanation:
In the given rhombus PQRS,
m∠SPQ = m∠SPR + m∠QPR
By substituting the given values,
m∠SPQ = (4x + 11)° + (5x - 4)°
= (4x + 5x) + (11 - 4)
= 9x + 7
Therefore, m∠SPQ = (9x + 7)° will be the answer.
Oscar built a train-track board for his trains. The shape of the board is drawn on the grid. Notice that the intervals on each axis are 2 feet. What is the area of the board?
A) 28 square feet
B) 121 square feet
C) 120 square feet
D) 110 square feet

Answers
The requried area of the board is 110 square feet, option D is correct.
From the figure,
The length of the board is 11 feet
The width of the board is 10 feet
The area of the board is given as:
Area = length x width
Area = 11 × 10
Area = 110 square feet.
Thus, the requried area of the board is 110 square feet, and option D is correct.
Learn more about the area of a rectangle here:
https://brainly.com/question/20693059
#SPJ1
8x + 3 = 14
find what x is to get to 14
Answers
Step-by-step explanation:
To find the value of x, we need to isolate it on one side of the equation.
First, we can subtract 3 from both sides:
8x + 3 - 3 = 14 - 3
This simplifies to:
8x = 11
Next, we can divide both sides by 8:
8x/8 = 11/8
This gives us:
x = 11/8
So the value of x that will get us to 14 is 11/8.
Hope this helps
So 8x=11
11/8=1.375