Answers
Laasya is performing resistance training by lifting a table and moving it to another room to expand the space in her room. The correct option to this question is D.
Strength training By putting your muscles up against resistance, resistance training builds muscle strength. Free weights, weight machines, resistance bands, and your own body weight are all used in various types of resistance training. To get the most out of their training, beginners should go two or three times per week.Resistance training is founded on the idea that, when called upon, the body's muscles will struggle to overcome a resisting force. Resistance exercise has both advantages and disadvantages.Resistance exercises include planks, sit-ups, squats, push-ups, leg raises, and leg extensions. You and a small amount of room are all that are needed for these strength training exercises.For more information on resistance training kindly visit to
https://brainly.com/question/28936785
#SPJ1
Complete question : Laasya is lifting a table and moving it to another room to expand the space in her room. What mode of strength-training is Laasya performing?
a. Endurance
b. Isometric
c. Isotonic
d. Resistance
Related Questions
A 0.0400 kg meter stick is placed on a thin rod at the 30.0 cm mark. What is the minimum mass required to be placed on the 0.00 cm mark on the stick to maintain equilibrium?
Answer in kg
Answers
The minimum mass required to be placed on the 0.00 cm mark of the meter stick to maintain equilibrium is 0.120 kg.
To maintain equilibrium, the torques acting on the meter stick must balance each other. The torque is given by the formula:
τ = r * F * sin(θ)
where τ is the torque, r is the distance from the pivot point to the point where the force is applied, F is the force applied, and θ is the angle between the force vector and the lever arm.
In this case, the meter stick is in equilibrium when the torques on both sides of the pivot point cancel each other out. The torque due to the weight of the meter stick itself is acting at the center of mass of the meter stick, which is at the 50.0 cm mark.
Let's denote the mass to be placed on the 0.00 cm mark as M. The torque due to the weight of M can be calculated as:
τ_M = r_M * F_M * sin(θ)
where r_M is the distance from the pivot point to the 0.00 cm mark (which is 30.0 cm), F_M is the weight of M, and θ is the angle between the weight vector and the lever arm.
Since the system is in equilibrium, the torques on both sides of the pivot point must be equal:
τ_M = τ_stick
r_M * F_M * sin(θ) = r_stick * F_stick * sin(θ)
Substituting the given values:
30.0 cm * F_M = 20.0 cm * (0.0400 kg * 9.8 m/s^2)
Solving for F_M:
F_M = (20.0 cm / 30.0 cm) * (0.0400 kg * 9.8 m/s^2)
F_M = 0.0264 kg * 9.8 m/s^2
F_M = 0.25872 N
Finally, we can convert the force into mass using the formula:
F = m * g
0.25872 N = M * 9.8 m/s^2
M = 0.0264 kg
Therefore, the minimum mass required to be placed on the 0.00 cm mark of the meter stick to maintain equilibrium is 0.120 kg.
For more such questions on equilibrium, click on:
https://brainly.com/question/517289
#SPJ8
Question 1 of 10
A business must decide whether to open a new office in China. If it opens the
branch, it will increase its chances of selling a high volume of its products in
China. On the other hand, the business will have to spend a lot of money to
make the branch operational.
What would be an opportunity cost for the business if it chooses not to open
the new branch in China?
A. The business would lose the chance to make more money in
China.
B. The business would increase its marginal benefits on each
product it makes.
Answers
Opportunity cost refers to the cost of the next best alternative that must be forgone in order to pursue a certain action. In this case, if the business chooses not to open the new branch in China, the opportunity cost would be the potential revenue and profits that could have been generated by selling products in China.
What is the speed of a car traveling 100 m in 20 s?
Answers
Answer: To answer this question, we will need the following equation: SPEED = DISTANCE/TIME (A multiplication and division triangle will be shown)i) The speed of the car is calculated by doing 100 metres/ 20 seconds which gives us 5 metres per second. ii) Rearranging the equation earlier, we can make the distance the subject of the equation so that we get SPEED x TIME = DISTANCE. We worked out the speed and the time was given as 1 minute 40 seconds but we cannot plug in the numbers yet as the time has to be converted to units of seconds (because our speed is in meters per second). 1 minute 40 seconds = 60 seconds + 40 seconds = 100 secondsWe then plug in the numbers to get the distance travelled = 5 metres per second x 100 seconds = 500 metres.
Explanation:
An elevator moves upward while increasing speed. Which of the following statements comparing the force of the cable on the elevator T and the weight of the elevator W is correct?
Answers
Explanation- T and W are inversely related on the elevators y-axis, T pointing up and W (mass of object multiplied by gravity) pointing down. When T+W=0, the object would not be moving. Since the elevator is moving up, T must be a larger force since it neglects W and moves up. Therefore F=T-W
Answer:
See below
Explanation:
Downward force = weight = mg where g = accel of gravity 9.81 m/s ^2
the tension force acting UPWARD to cause the elevator to accelerate upward is F = T=m(a+g) where ' a ' is the UPWARD acceleration ...the tension must be equal to
the weight of the object + mass of object* acceleration
Verify that the quantity (k/N)Inr, where In,) is equal to the (mean) entropy of the given system. Show that this leads to essentially the same result for In T if we take, in the foregoing summation, only the largest term of the sum, namely the term Wint) that corresponds to the most probable distribution set. ISurprised? Well, note the following example: For all N, the summation over the binomial coefficients N!/Ir! (N-r!)l gives CNG, 2 r-0 therefore nCNIn2. Now, the largest term in this sum corresponds to r N/2; so, for large N, the logarithm of the largest term is very nearly equal to In(N!)-2In((N/2)!) N, N which agrees with (a).J
Answers
Because one mole of H X 2 is typically lighter than N e, it stands to reason that it would have a higher entropy than N e. Ne, on the other hand, is thought to have a higher entropy due to its lower molar mass.
A chemical equation can be examined for changes in physical states and the number of moles of product and reactant particles to predict relative changes in entropy using the same factors on a macroscopic level.
The species with the greater molar mass between two monoatomic ones will have a greater standard entropy. The more mobile of two allotropic forms of an element will have a higher standard entropy value. The entropies of these substances are not zero, despite the fact that their conventional internal energies and enthalpies would be. The "energies of formation" of elements in their normal states are typically set to zero because there is no absolute scale of energy.
Entropy, on the other hand, gauges the distribution of energy among the numerous quantum states that can accept it; they exist even in pure substances.
Evidently, entropies often rise with molecule weight. This is, of course, a direct reflection of the fact that translational quantum states are more densely packed in heavier molecules, making them more occupiable, for the noble gases.
The additional impacts of rotational quantum levels are visible in the entropies of the diatomic and polyatomic molecules.
To know more about entropy
https://brainly.com/question/13146879
#SPJ4
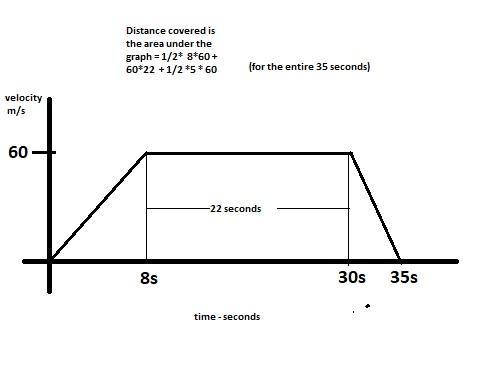
A car accelerated uniformly from rest and attained a velocity of 8m/s. it then travels with the uniform velocity of for the next 22 seconds and later brought to rest in 5 seconds
(a )draw the velocity time graph
(b.) calculate the total distance covered (c.) calculate the distance covered after 25 seconds.
Answers
Answer:
See below
Explanation:
See diagram below
8 seconds to 60 m/s then 60 m/s for 22 seconds then to 0 m/s in 5 seconds
5) What is the weight of a body in earth. if its weight is 5Newton
in moon?
Answers
Answer:
8.167
Explanation:
A force of 525 N is applied to a stationary couch of mass 100 kg, where μs = 0.40 and μk = 0.32. What is the acceleration of the couch
Answers
Answer:
Approximately \(2.11\; \rm m\cdot s^{-2}\) (assuming that \(g = 9.81\; \rm m\cdot s^{-2}\), the floor is horizontal, and that the external force is applied horizontally.)
Explanation:
The mass of this couch is \(m = 100\; \rm kg\). Calculate the weight of the couch:
\(W = m \cdot g = 100\; \rm kg \times 9.81\; \rm m \cdot s^{-2} = 981\; \rm N\).
Assume that the floor is horizontal. The magnitude of the normal force between the floor and the couch would be equal to the size of the weight of this couch.
Therefore, the normal force between the floor and the couch would be \(N = 981\; \rm N\).
The first step is to find out whether the couch would move at all.
The question has provided two constants of friction: \(\mu_\text{s}\) (coefficient of static friction) and \(\mu_\text{k}\) (coefficient of kinetic friction.)
The coefficient of static friction applies when the couch is stationary relative to the floor: \(f_\text{s} = \mu_\text{s} \cdot N = 0.40\times 981\; \rm N \approx 313.92\; \rm N\). In other words, while the couch isn't moving, the maximum (horizontal) external force that friction could resist would be \(f_\text{s} = 313.92\; \rm N\).
Assume that the external force in this question is horizontal. The size of the external force (\(525\; \rm N\)) exceeds that of \(f_\text{s}\). Hence, the couch would start to move after the \(525\; \rm N\!\) external force is applied.
Once the couch starts to move, the coefficient of static friction would no longer be relevant. Instead, the coefficient of kinetic friction (\(\mu_\text{k}\)) would give size of the friction between the floor and the couch. The size of that friction would be \(f_\text{k} = \mu_\text{k} \cdot N = 0.32\times 981\; \rm N \approx 313.92\; \rm N\).
This friction would counteract the horizontal external force on the couch. Hence, the net force on the couch in the horizontal direction would be:
\(\begin{aligned}& F(\text{external}) - f_\text{k} \\ &\approx 525\; \rm N - 313.92\; \rm N \\ &\approx 211.08\; \rm N \end{aligned}\).
Apply Newton's Second Law of motion to find the acceleration of the couch:
\(\begin{aligned}a &= \frac{(\text{Net Force})}{m} \\ & \approx \frac{211.08\; \rm N}{100\; \rm kg} \approx 2.11\; \rm m \cdot s^{-2}\end{aligned}\).
Which of the following is NOT true about the mass of an object?
A)
Mass is measured in kilograms.
B)
Mass is a measurement of force.
C)
Mass is a measurement of the amount of matter in an object.
D)
Mass does not change based on your location.
Answers
Answer:
B) Mass is a measurement of force
Explanation:
Mass is not a measurement of force, mass is a measurement of the amount of matter in an object.
What I need help with is attached below

Answers
Answer:
Explanation:
3. answer is d.
Displacement increases b/c slopes of both lines are positive. Spring 1 displaces more than Spring 2 per unit force applied. Graphs are straight lines, so the increase is proportional.
4. Fnet = 5 - 30 - 5 = -30 N Positive direction is to the right, negative direction is to the left.
answer is d. 30 N to the LEFT
The operating temperature of a tungsten filament in an incandescent light bulb is 2450 K, and its emissivity is 0.350. Find the surface area of the filament of a 150 W bulb if all the electrical energy consumed by the bulb is radiated by the filament as electromagnetic waves. (Only a fraction of the radiation ap- pears as visible light.)
Answers
Answer:
A = 2.1 × 10^(-4) m²
Explanation:
We are given;
Temperature; T = 2450 K
Emissivity; ε = 0.35
Bulb rating; H = 150 W
To calculate the surface area, we will use the formula;
H = AεσT⁴
Where σ is stephan boltzman constant with a value of 5.66 × 10^(−8) W/m²⋅K⁴
Making A the subject of the formula, we have;
A = H/εσT⁴
Plugging in the relevant values gives;
A = 150/(0.35 × 5.66 × 10^(−8) × 2450⁴)
A = 2.1 × 10^(-4) m²
how many newtons does a 190 lb person weigh? express your answer in newtons. activate to select the appropriate template from the following choices. operate up and down arrow for selection and press enter to choose the input value typeactivate to select the appropriates symbol from the following choices. operate up and down arrow for selection and press enter to choose the input value type w
Answers
The weight of a 190 lb person is 844.5 N.
What is the definition of 1 Newton?Newton is the SI (International System) unit of force, named after Sir Isaac Newton, a famous physicist, and mathematician. It is defined as the force required to accelerate a mass of one kilogram at a rate of one meter per second squared (1 N = 1 kg m/s²).
To convert pounds (lb) to Newtons (N), we need to use the conversion factor:
1 lb = 4.45 N
Therefore, a 190 lb person weighs:
190 lb × 4.45 N/lb = 844.5 N
So the weight of a 190 lb person is 844.5 N.
Learn more about Newton here:
https://brainly.com/question/20389058
#SPJ1
A disk with a rotational inertia of 2.5 kg-m2 and a radius 1.1 m rotates on a frictionless fixed axis perpendicular to the disk faces and through its center. A force of 7.7 N is applied tangentially to the rim. The angular acceleration of the disk is _____ rad/s2. Round your answer to the nearest tenth.
Answers
Answer:
3.4 rad/sec^2
Explanation:
rotational inertia = 2.5 kg-m^2 radius = 1.1 m force = 7.7 N
t = rotational inertia * angular acceleration equation 1
also t = force * radius
therefore to calculate angular acceleration equation 1 becomes
f * r = inertia * angular acceleration hence
angular acceleration = f * r / inertia = \(\frac{7.7 * 1.1 }{2.5}\) 8.47 / 2.5 = 3.388 ≈ 3.4 rad/sec^2
Explain/Describe how atoms in domains determine whether a material is magnetic or not. (Please help this is due today)
Answers
Answer:
In a material, the magnetic behavior depends on the alignment of magnetic moments of the atoms. Magnetic moments are generated by the motion of the electrons in the atoms. When the magnetic moments of atoms in a material are aligned in a specific pattern, it creates a magnetic field which results in the material being magnetic.
In many materials, the magnetic behavior arises due to the alignment of magnetic domains, which are regions of atoms with magnetic moments aligned in the same direction. When many domains with aligned magnetic moments are present in a material, the material becomes magnetic.
The magnetic behavior of a material depends on the number of electrons and the arrangement of those electrons in the atoms. In particular, for an atom to have a magnetic moment, it must have unpaired electrons, meaning electrons that are not paired with another electron with the opposite spin. When these unpaired electrons in the atoms are aligned, they generate a magnetic moment. If all electrons are paired, there will not be a net magnetic moment, so the material will not be magnetic.
So, in summary, the magnetic behavior of a material is determined by the alignment of magnetic moments of atoms. When the magnetic moments of many atoms in a material align in the same direction, it creates a magnetic field, leading to a material being magnetic. This alignment is usually present in magnetic domains consisting of atoms with unpaired electrons.
Two point charges, 3.4 μC and -2.0 μC , are placed 5.0 cm apart on the x axis. Assume that the negative charge is at the origin, and the positive x-axis is directed from the negative charge to the positive. At what points along the x axis is the potential zero? Let V=0 at r=∞ .
Answers
The electric field is zero at x = -16.45cm
Data;
q1 = 3.4 μC q2 = -2.0 μC distance = 5cmThe Electric Field at point 0As the 3μC is larger than -2.0μC and the charges are opposite sign. The electric field will be zero at the negative axis.
Let the point be at x.
For an electric field to be equal to zero;
\(k(\frac{q_1}{d_1})^2 + k(\frac{q_2}{d_2})^2 = 0\\\frac{3.4}{(5-x)^2} - \frac{2}{x^2} = 0\\\)
Let's solve for x using mathematical methods.
\(\frac{3.4x^2 - 2(5-x)^2}{(5-x)^2x^2}= 0\\ 3.4x^2 - 2(5-x^2) = 0\\3.4x^2 - 50 - 2x^2 + 20x = 0\\1.4x^2 +20x - 50 = 0\)
Solving the above quadratic equation;
\(x = -16.45cm\)
The electric field is zero at x = -16.45cm
Learn more on electric field at a point here;
https://brainly.com/question/1592046
https://brainly.com/question/14372859
A horizontal force of 20 N just starts to move a box with weight80 N. Find the value of coefficient of static friction.
Answers
The static friction formula is
\(\begin{gathered} F_s=\mu_sN \\ \mu_s=\frac{F_s}{mg} \end{gathered}\)As you can observe, the normal force is equal to the weight force.
\(\mu_s=\frac{20N}{80N}=0.25\)Therefore, the value of the coefficient of static friction is 0.25.
__________ energy always moves from a warmer object to a cooler object.
A) electromagnetic
B) nuclear
C) thermal
Answers
An unhappy 0.400 kg rodent, moving on the end of a spring with force constant 3.50 N/m , is acted on by a damping force Fx=−bvx .
Answers
The equation of motion for the rodent is x(t) = -1.12cos(3.20t), and the damping force is Fd = -0.62*vx(t). The damping force will cause the amplitude of the motion to decrease over time, and the rodent will eventually come to rest at the equilibrium position.
We can use the following equations to solve this problem:
F = -kx (Hooke's Law)
F = ma (Newton's Second Law)
a = d^2x/dt^2 (Definition of Acceleration)
Fd = -bv (Definition of Damping Force)
x(t) = A*cos(ωt + φ) (Equation of Motion for Simple Harmonic Motion)
We will need to use these equations to find the displacement, velocity, and acceleration of the rodent as a function of time, and then use that information to calculate the damping force and solve for the parameters of the motion.
First, let's find the natural frequency of the system:
ω = sqrt(k/m) = sqrt(3.50 N/m / 0.400 kg) = 3.20 rad/s
Next, let's assume that the rodent starts at its maximum displacement and moves in simple harmonic motion. We can use the equation of motion for simple harmonic motion to write:
x(t) = A*cos(ωt + φ)
where A is the amplitude of the motion and φ is the phase angle.
To find A and φ, we need to use the initial conditions. We know that at t=0, the rodent is at its maximum displacement, so x(0) = A. We also know that at t=0, the velocity of the rodent is zero, so vx(0) = -Aωsin(φ) = 0. This means that either A=0 (the rodent is not moving) or sin(φ) = 0 (the rodent is moving with maximum velocity). We will assume that the latter is true, so sin(φ) = 0 and cos(φ) = 1.
Now we can write:
x(t) = A*cos(ωt)
To find A, we use the fact that the rodent has a mass of 0.400 kg and is moving on a spring with force constant 3.50 N/m. The force on the rodent is given by:
F = -kx = -3.50 N/m * A*cos(ωt)
At maximum displacement, the force is equal to the weight of the rodent:
mg = 0.400 kg * 9.81 m/s^2 = 3.92 N
So we can write:
3.92 N = -3.50 N/m * A
A = -1.12 m
Therefore, the equation of motion for the rodent is:
x(t) = -1.12cos(3.20t)
To find the velocity and acceleration of the rodent, we take the derivative of the displacement with respect to time:
vx(t) = dx/dt = 3.58sin(3.20t)
ax(t) = d^2x/dt^2 = -11.46cos(3.20t)
To find the damping force, we use the equation:
Fd = -bv = -bdx/dt = -b3.58sin(3.20t)
We don't know the value of b, so we can't solve for it directly. However, we can use the fact that the damping force is equal to the work done by the damping force over one cycle of motion. This work is equal to the energy lost by the system due to damping. Since the system is losing energy at a rate proportional to its velocity, we can write:
Energy lost per cycle = Average damping force * Distance traveled per cycle
The distance traveled per cycle is equal to 2piA = 7.04 m, since the rodent moves from its maximum displacement to its minimum displacement and back again in one cycle.
The average damping force over one cycle is equal to the time average of the damping force:
<Fd> = (1/T)∫[0,T] -bdx/dt dt
where T = 2*pi/ω is the period of the motion. Evaluating the integral gives:
<Fd> = (1/T)∫[0,T] -b(-1.12)3.20sin(3.20*t) dt
<Fd> = 3.58*b
Since the energy lost per cycle is also equal to (1/2)kA^2, we can write:
(1/2)kA^2 = <Fd>2pi*A
Solving for b, we get:
b = (kA)/(2pi)
Substituting the given values, we get:
b = (3.50 N/m * 1.12 m)/(2*pi) = 0.62 Ns/m
Therefore, the equation of motion for the rodent is:
x(t) = -1.12cos(3.20t)
vx(t) = 3.58sin(3.20t)
ax(t) = -11.46cos(3.20t)
and the damping force is given by:
Fd = -0.62*vx(t)
Note that the negative sign indicates that the damping force acts in the opposite direction to the velocity of the rodent. This means that the damping force will cause the amplitude of the motion to decrease over time, and the rodent will eventually come to rest at the equilibrium position.
Therefore,The equation of motion for the rodent is x(t) = -1.12cos(3.20t), and the damping force is Fd = -0.62*vx(t).
To learn more about Newton's law of motion click:
brainly.com/question/29775827
#SPJ1
A 10-cm-thick aluminum plate (α = 97.1 × 10−6 m2/s) is being heated in liquid with temperature of 550°C. The aluminum plate has a uniform initial temperature of 25°C. If the surface temperature of the aluminum plate is approximately the liquid temperature, determine the temperature at the center plane of the aluminum plate after 15 s of heating. Solve this problem using the analytical one-term approximation method. The temperature at the center plane after 15 s of heating is
Answers
Answer:
356°C.
Explanation:
(1). The first step to the solution to this particular Question/problem is to determine the Biot number, and after that to check the equivalent value of the Biot number with plate constants.
That is, Biot number = (length × ∞)÷ thermal conductivity. Which gives us the answer as ∞. Therefore, the equivalent value of the ∞ on the plates constant = 1.2732 for A and 1.5708 for λ.
(2). The next thing to do is to determine the fourier number.
fourier number = [α = 97.1 × 10−6 m2/s × 15 s] ÷ (.05m)^2 = 0.5826.
(3). The next thing is to determine the temperature at the center plane after 15 s of heating.
The temperature at the center plane after 15 s of heating = 500°C [ 25°C - 500°C ] [1.2732] × e^(-1.5708)^2 ( 0.5826).
The temperature at the center plane after 15 s of heating = 356°C.
Bob is driving at 25.5 m/s when a deer steps into the road 52 m ahead of him. Assuming Bob immediately hits the
brakes and has a maximum braking acceleration of 7.2 m/s², will he be able to stop in time or will he hit the deer?
How many significant figures should the answer to this problem have?
Answers
Answer:
Bob will be able to stop in time.
I think the final answer should be reported to two significant figures.
Explanation:
First, it is necessary to calculate the time (in s) it takes ol' Bob to stop his vehicle. Use kinematic equation #1 and the given data to determine the time. For this problem, let
\(V_i=25.5\frac{m}{s}\\V_f=0.0\frac{m}{s}\\a=-7.2\frac{m}{s^2}\)
Acceleration is a negative value because it opposes the current motion of the vehicle.
So,
\(V_f=V_i+at\\0.0\frac{m}{s}=25.5\frac{m}{s}+(-7.2\frac{m}{s^2})t\\-25.5\frac{m}{s}=(-7.2\frac{m}{s^2})t\\3.5s=t\)
Next, use kinematic equation #2 and the calculated time to solve for Δx:
\(\Delta x=(\frac{V_i+V_f}{2})t\\\Delta x=(\frac{25.5\frac{m}{s}+0.0\frac{m}{s}}{2})(3.5s)\\\Delta x=(12.75\frac{m}{s})(3.5s)\\\Delta x=45.2m\)
45.2m < 52m, so Bob and our crepuscular ungulate will not bump into each other.
I would say that the final answer should have two significant figures because the value for acceleration is given to two significant figures. The rules for significant figures state that when multiplying or dividing, the number of significant figures in the answer is determined by the value with the lowest number of significant figures. So, the value for time can only be recorded as having two significant figures. Since time is used as a multiplier to determine the distance traveled, the final answer should also be reported to two significant figures. I think.
Calculate the electric potential at the center of the square described as follows: Four charges are placed at the corners of a 20 cm square. The particles are as follows: 10 microC at x =0, y = 0, -5 microC at x = 20, y = 0, -15 microC at x = 20, y = 20, and 20 microC at x=0 and y = 20 .
Answers
, the answer is 2020 kV
Explanation
Electric potential of a point charge is
\(\begin{gathered} V=\frac{KQ}{d} \\ where\text{ kis a constant k=9*10}^9\text{ N*}\frac{m^2}{C^2} \\ Q\text{ is charge , d is the distance} \end{gathered}\)so
Step 1
Diagram:
Step 2
distances:fromthe center to each charge:
:
\(\begin{gathered} d=\sqrt{0.10^2+0.10^2}=\sqrt{0.02}\text{ m=0.1414m} \\ d=0.1414\text{ m} \end{gathered}\)
Step 3
electric potential due to each charge.
a) Q1
\(\begin{gathered} V=\frac{KQ}{d} \\ V=\text{9*10}^9\text{ N*}\frac{m^2}{C^2}*\frac{10*10^{-6}C}{0.1414\text{ m}} \\ V=636.49\text{ kV} \\ \end{gathered}\)b)Q2
\(\begin{gathered} V=\frac{KQ}{d} \\ V=\text{9*10}^9\text{ N*}\frac{m^2}{C^2}*\frac{-5*10^{-6}C}{0.1414\text{ m}} \\ V=-318.24\text{ KV} \\ \end{gathered}\)c)Q3
\(\begin{gathered} V=\frac{KQ}{d} \\ V=\text{9*10}^9\text{ N*}\frac{m^2}{C^2}*\frac{-15*10^{-6}C}{0.1414\text{ m}} \\ V=-954.73\text{kV} \\ \end{gathered}\)d)Q4
\(\begin{gathered} V=\frac{KQ}{d} \\ V=\text{9*10}^9\text{ N*}\frac{m^2}{C^2}*\frac{20*10^{-6}C}{0.1414\text{ m}} \\ V=-954.73\text{kV} \\ V=1272.98\text{ kV} \end{gathered}\)so, the resultant electric potential are:
:
So
\(\begin{gathered} v=\sqrt{1309.2^2+1591.22^2} \\ v=2060\text{ Kv} \end{gathered}\)therefore, the answer is 2020 kV
I hope this helps you




URGENT!!! 50 POINTS NO CHATGPT!
A fisherman notices that his boat is moving up and down periodically without any horizontal motion, owing to waves on the surface of the water It takes a time of 3.00 s for the boat to travel from its highest point to its lowest, a total distance of 0.650 m
mThe fisherman sees that the wave crests are spaced a horizontal distance of 5.90 m apart
Part A
How fast are the waves traveling?
Express the speed v in meters per second using three significant figures.
What is the amplitude A of each wave?
Express your answer in meters using three significant figures.
Answers
Answer:
Part A: \(1.97ms^{-1}\) (2 s.f.)
Part B: 0.33m (2 s.f.)
Explanation:
Part A:
Frequency = \(\frac{1}{period} = \frac{1}{3}\) Hz
Wavespeed = frequency x wavelength
Wavelength = distance between two crests = 5.90
Freq = 1/3 Hz
Therefore: Wavespeed = 1/3 x 5.90
Wavespeed = 1.967 ms^-1
Part B:
Amplitude = \(\frac{peak-to-peak- amplitude }{2}\)
Peak to peak amplitude = 0.65m
Amplitude = 0.65/2 = 0.325m = 0.33m 2sf
does the mass of a parachute affect terminal velocity?
Answers
Answer:
The greater weight increases the terminal velocity by acting as an extra force against gravity and air resistance.
Four passengers with combined mass 250 kg compress the springs of a car with worn out shock absorbers by 4.00cm when they enter it. Model the care and passengers as a single body on a single ideal spring. If the loaded has a period of vibration of 1.08 s, what is the period of vibration of the empty car?
Answers
Answer:
The time period of the empty car will be "1.00 s".
Explanation:
The given values in the question will be:
Mass,
m = 250 kg
Loaded car's time period will be:
T = 1.08 s
Shock absorbers compression,
x = 4 cm
or,
= 0.04 m
Now,
Weight of passengers will be:
⇒ \(F=mg\)
\(=250\times 9.8\)
\(=2450 \ N\)
The spring constant of shock absorbers will be:
⇒ \(k=\frac{F}{x}\)
\(=\frac{2450}{0.04}\)
\(=61.250 \ N/m\)
As we know,
Time period, \(T = 2 \pi\sqrt{\frac{M}{k} }\)
On substituting the values, we get
\(1.08=2\pi \sqrt{\frac{M}{61250} }\)
\(\frac{M}{61250}=0.02955\)
\(M=0.02955\times 61250\)
\(=1809.6 \ kg\) (Total mass of car as well as its passengers)
Now,
The mass of the empty car will be:
⇒ \(m'=M-m\)
\(=1809.6-250\)
\(=1559.6 \ kg\)
hence,
The time period of empty car will be:
⇒ \(T'=2\pi\sqrt{\frac{m'}{k} }\)
\(=2\pi\sqrt{\frac{1559.6}{61250} }\)
\(=2\pi \sqrt{0.0254}\)
\(=1.003 \ s\)
or,
\(=1.00 \ s\)
In this image of an atom, what does the outer area consisting of tiny blue
dots represent?
O A. The electron cloud
B. Protons
C. The nucleus
D. Neutrons

Answers
A 1000 kg compact car stops without skidding on asphalt with a
coefficient of friction of 0.85. What is the stopping distance of the car if it was originally traveling at 27 m/s?
Answers
43.8 m
Explanation:
The only force acting on the car is the frictional force f and since friction is a force that is always directed opposite to the direction of motion, it will have a negative sign. Therefore, we can write Newton's 2nd law as
\(x:\;\;\;\;F_{net} = -f = -\mu N = ma\) (1)
\(y:\;\;\;\;F_{net} = N - mg = 0\) (2)
Substituting Eqn(2) into Eqn(1), we get
\(\Rightarrow a = -\mu g\) (3)
To find the stopping distance x, we are going to use the equation
\(v^2 = v_0^2 + 2ax\)
Initially, the car was moving at \(v_0 = 27\:\text{m/s}.\) When it stopped, its final velocity \(v\) is zero. Using these, as well as Eqn(3) on the equation for v^2, we find that
\(0 = v_0^2 + 2(-\mu g)x \Rightarrow 0 = v_0^2 - 2\mu gx\)
or solving for x,
\(x = \dfrac{v_0^2}{2\mu g} = \dfrac{(27\:\text{m/s})^2}{2(0.85)(9.8\:\text{m/s}^2)}\)
\(\:\:\:\:= 43.8\:\text{m}\)
should money be used for space travel when there are so many serious problems on Earth to be addressed? explain your answer.
Answers
Answer:
Anyway, space exploration absolutely does give us a direct benefit. When space technology has advanced far enough, we will be able to leave this planet in large numbers and live among the stars. This will solve our population/environment/resource/energy problems for a long, long time. Even a fraction of the money spent annually on space exploration could save millions of people in poverty-stricken countries, and improve living conditions for future generations. The foundations of the world we live in are largely based on science and it is indeed vital to extend our knowledge of the universe.
Thank You
Please mark me brainliest
What is the net force (in N) of a 3.00 N force and an 8.00 N force acting on an object for each of the following conditions?
b) The forces act in the same direction.
Answers
8N+3N=11N
This is because the two forces are acting in the same direction, so there is an additional 3N of force added to the 8N of force.
If an object moves for 0.098 seconds, how long did it move in milliseconds (ms)?
A) 98 ms
B) 980 ms
C) 0.000098 ms
D) 9.8 ms
Answers
The amount of energy needed to a power a 0.20kw bulb for one minute would be just sufficient to lift a 2.5 kg object through a vertical distance of
Answers
The amount of energy needed to power a 0.20 kW bulb for one minute would be just sufficient to lift a 2.5 kg object through a vertical distance of approximately 29.03 meters.
To calculate the energy required to lift a 2.5 kg object through a vertical distance, we need to consider the gravitational potential energy formula:
Potential energy (PE) = mass (m) × gravity (g) × height (h)
Where:
m = 2.5 kg (mass of the object)
g = 9.8 m/s² (acceleration due to gravity on Earth)
h = ? (height)
First, let's find the height (h) by rearranging the formula:
h = PE / (m × g)
Now, let's calculate the potential energy (PE) needed to lift the object. We are given that the power of the bulb is 0.20 kW, and we want to find the energy required for one minute. To convert kilowatts (kW) to joules (J), we multiply by the conversion factor of 3,600 (60 seconds × 60 minutes):
Energy (E) = power (P) × time (t)
E = 0.20 kW × 1 min × 3,600 J/kW
Now, we can substitute the values into the equation to find the height:
h = (0.20 kW × 1 min × 3,600 J/kW) / (2.5 kg × 9.8 m/s²)
Calculating the expression on the right side:
h ≈ 0.20 × 1 × 3,600 / (2.5 × 9.8) ≈ 29.03 meters (rounded to two decimal places)
Therefore, the amount of energy needed to power a 0.20 kW bulb for one minute would be just sufficient to lift a 2.5 kg object through a vertical distance of approximately 29.03 meters.
For more such questions on Energy & Power
https://brainly.com/question/1634438
#SPJ11